Studio di Funzioni Logaritmiche

Dominio:

Affinché la funzione sia definita, l'argomento del logaritmo deve essere strettamente positivo. Quindi, \( x > 0 \) → \( (0, +\infty) \).

Intersezioni con gli assi:

Intersezione con l'asse y: Non esiste, poiché \( x = 0 \) non appartiene al dominio.

Intersezione con l'asse x: Poniamo \( y = 0 \), quindi \( (\ln(x))^2 - \ln(x) = 0 \). Sia \( t = \ln(x) \), allora \( t^2 - t = 0 \), da cui \( t(t - 1) = 0 \). Questo implica \( t = 0 \) o \( t = 1 \).

• Se \( t = 0 \), allora \( \ln(x) = 0 \), quindi \( x = e^0 = 1 \). Punto di intersezione: \( (1, 0) \).
• Se \( t = 1 \), allora \( \ln(x) = 1 \), quindi \( x = e^1 = e \). Punto di intersezione: \( (e, 0) \).

Segno della funzione:

Studiamo il segno di \( (\ln(x))^2 - \ln(x) > 0 \). Ponendo \( t = \ln(x) \), abbiamo \( t^2 - t > 0 \), ovvero \( t(t - 1) > 0 \). Questa disequazione è soddisfatta se \( t < 0 \) o \( t > 1 \).

• Se \( \ln(x) < 0 \), allora \( 0 < x < e^0 = 1 \).
• Se \( \ln(x) > 1 \), allora \( x > e^1 = e \).

Quindi, la funzione è positiva per \( x \in (0, 1) \cup (e, +\infty) \) e negativa per \( x \in (1, e) \).

Limiti:

• Limite per \( x \to 0^+ \): \( \lim_{x \to 0^+} ((\ln(x))^2 - \ln(x)) \). Sia \( t = \ln(x) \), quando \( x \to 0^+ \), \( t \to -\infty \). Quindi il limite diventa \( \lim_{t \to -\infty} (t^2 - t) = +\infty \).
• Limite per \( x \to +\infty \): \( \lim_{x \to +\infty} ((\ln(x))^2 - \ln(x)) = +\infty \), poiché \( (\ln(x))^2 \) cresce più rapidamente di \( \ln(x) \).

Asintoti:

• Asintoto verticale: Poiché \( \lim_{x \to 0^+} ((\ln(x))^2 - \ln(x)) = +\infty \), la retta \( x = 0 \) (l'asse y) è un asintoto verticale.
• Asintoti orizzontali: Non ci sono asintoti orizzontali poiché \( \lim_{x \to +\infty} ((\ln(x))^2 - \ln(x)) = +\infty \).
• Asintoti obliqui: Non ci sono asintoti obliqui perché il limite di \( \frac{f(x)}{x} \) per \( x \to +\infty \) è \( \lim_{x \to +\infty} \frac{(\ln(x))^2 - \ln(x)}{x} = 0 \) (per gerarchia degli infiniti), quindi \( m = 0 \), escludendo la possibilità di un asintoto obliquo.

Derivata prima:

\( f'(x) = \frac{d}{dx} [(\ln(x))^2 - \ln(x)] = 2 \ln(x) \cdot \frac{1}{x} - \frac{1}{x} = \frac{2 \ln(x) - 1}{x} \).

Studiamo il segno di \( f'(x) \): il denominatore \( x \) è sempre positivo nel dominio. Quindi il segno di \( f'(x) \) dipende dal segno del numeratore \( 2 \ln(x) - 1 \).

\( 2 \ln(x) - 1 > 0 \implies \ln(x) > \frac{1}{2} \implies x > e^{1/2} = \sqrt{e} \).

Quindi, la funzione è decrescente per \( 0 < x < \sqrt{e} \) e crescente per \( x > \sqrt{e} \). In \( x = \sqrt{e} \) c'è un punto di minimo relativo con ordinata \( f(\sqrt{e}) = (\ln(\sqrt{e}))^2 - \ln(\sqrt{e}) = (\frac{1}{2})^2 - \frac{1}{2} = \frac{1}{4} - \frac{1}{2} = -\frac{1}{4} \). Il punto di minimo è \( (\sqrt{e}, -\frac{1}{4}) \).

Derivata seconda:

\( f''(x) = \frac{d}{dx} \left[ \frac{2 \ln(x) - 1}{x} \right] = \frac{\frac{2}{x} \cdot x - (2 \ln(x) - 1) \cdot 1}{x^2} = \frac{2 - 2 \ln(x) + 1}{x^2} = \frac{3 - 2 \ln(x)}{x^2} \).

Studiamo il segno di \( f''(x) \): il denominatore \( x^2 \) è sempre positivo nel dominio. Quindi il segno di \( f''(x) \) dipende dal segno del numeratore \( 3 - 2 \ln(x) \).

\( 3 - 2 \ln(x) > 0 \implies \ln(x) < \frac{3}{2} \implies x < e^{3/2} = e \sqrt{e} \).

Quindi, la concavità è verso l'alto per \( 0 < x < e \sqrt{e} \) e verso il basso per \( x > e \sqrt{e} \). In \( x = e \sqrt{e} \) c'è un punto di flesso con ordinata \( f(e \sqrt{e}) = (\ln(e^{3/2}))^2 - \ln(e^{3/2}) = (\frac{3}{2})^2 - \frac{3}{2} = \frac{9}{4} - \frac{6}{4} = \frac{3}{4} \). Il punto di flesso è \( (e \sqrt{e}, \frac{3}{4}) \).

Grafico della Funzione

Dominio:

La funzione è definita per \( x > 0 \), quindi il dominio è \( (0, +\infty) \).

Intersezioni con gli assi:

Non ci possono essere intersezioni con l’asse y, essendo \( x > 0 \).

Se \( y = 0 \), allora \( x \ln(x) - \frac{3}{2}x = 0 \). Poiché \( x > 0 \), possiamo dividere per \( x \) ottenendo \( \ln(x) - \frac{3}{2} = 0 \), da cui \( \ln(x) = \frac{3}{2} \), e quindi \( x = e^{3/2} = e \sqrt{e} \). Il punto di intersezione con l'asse x è \( (e \sqrt{e}, 0) \).

Segno della funzione:

Il segno di \( f(x) = x (\ln(x) - \frac{3}{2}) \) dipende dal segno di \( \ln(x) - \frac{3}{2} \) poiché \( x > 0 \).

• \( f(x) > 0 \) se \( \ln(x) - \frac{3}{2} > 0 \), ovvero \( \ln(x) > \frac{3}{2} \), quindi \( x > e^{3/2} = e \sqrt{e} \).
• \( f(x) < 0 \) se \( \ln(x) - \frac{3}{2} < 0 \), ovvero \( \ln(x) < \frac{3}{2} \), quindi \( 0 < x < e^{3/2} = e \sqrt{e} \).
• \( f(x) = 0 \) se \( x = e^{3/2} \).

Limiti alla frontiera del dominio:

• \( \lim_{x \to 0^+} (x \ln(x) - \frac{3}{2}x) \). Si ricorda il limite notevole \( \lim_{x \to 0^+} x \ln(x) = 0^- \). Quindi, \( \lim_{x \to 0^+} (x \ln(x) - \frac{3}{2}x) = 0^- , \) ricordando il segno della funzione.
• \( \lim_{x \to +\infty} (x \ln(x) - \frac{3}{2}x) = \lim_{x \to +\infty} x (\ln(x) - \frac{3}{2}) = +\infty \cdot (+\infty) = +\infty \).

Asintoti:

• Asintoto verticale: Non c'è asintoto verticale poiché \( \lim_{x \to 0^+} f(x) = 0 \) (il limite è finito).
• Asintoto orizzontale: Non c'è asintoto orizzontale poiché \( \lim_{x \to +\infty} f(x) = +\infty \).

Controlliamo se ci può essere asintoto obliquo:

• \( m = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{x \ln(x) - \frac{3}{2}x}{x} = \lim_{x \to +\infty} (\ln(x) - \frac{3}{2}) = +\infty \). Poiché \( m \) non è finito, non esiste asintoto obliquo.

Studio derivata prima:

\( f'(x) = \frac{d}{dx} (x \ln(x) - \frac{3}{2}x) = 1 \cdot \ln(x) + x \cdot \frac{1}{x} - \frac{3}{2} = \ln(x) + 1 - \frac{3}{2} = \ln(x) - \frac{1}{2} \).

• \( f'(x) > 0 \) se \( \ln(x) - \frac{1}{2} > 0 \), ovvero \( \ln(x) > \frac{1}{2} \), quindi \( x > e^{1/2} = \sqrt{e} \) (funzione crescente per \( x > \sqrt{e} \)).
• \( f'(x) < 0 \) se \( \ln(x) - \frac{1}{2} < 0 \), ovvero \( \ln(x) < \frac{1}{2} \), quindi \( 0 < x < e^{1/2} = \sqrt{e} \) (funzione decrescente per \( 0 < x < \sqrt{e} \)).
• \( f'(x) = 0 \) se \( \ln(x) = \frac{1}{2} \), ovvero \( x = \sqrt{e} \) è punto di minimo relativo (e assoluto).

Ordinata del minimo: \( f(\sqrt{e}) = \sqrt{e} \ln(\sqrt{e}) - \frac{3}{2}\sqrt{e} = \sqrt{e} \cdot \frac{1}{2} - \frac{3}{2}\sqrt{e} = -\sqrt{e} \).

Osserviamo che: \( \lim_{x \to 0^+} f'(x) = \lim_{x \to 0^+} (\ln(x) - \frac{1}{2}) = -\infty \), quindi il grafico della funzione si avvicina all’origine degli assi con tangente verticale.

Studio derivata seconda:

\( f''(x) = \frac{d}{dx} (\ln(x) - \frac{1}{2}) = \frac{1}{x} \).

Poiché per \( x > 0 \), \( f''(x) = \frac{1}{x} > 0 \), il grafico della funzione volge sempre la concavità verso l’alto, non ci sono flessi.

Grafico della Funzione

Dominio:

Affinché il logaritmo sia definito, l'argomento deve essere strettamente positivo: \( \frac{x+1}{x^2+2} > 0 \). Il denominatore \( x^2+2 \) è sempre positivo. Quindi, il segno della frazione dipende dal numeratore: \( x+1 > 0 \implies x > -1 \). Il dominio è quindi \( (-1, +\infty) \).

Intersezioni con gli assi:

Se \( x = 0 \), \( f(0) = \ln\left(\frac{0+1}{0^2+2}\right) = \ln\left(\frac{1}{2}\right) = -\ln(2) \). Punto di intersezione con l'asse y: \( (0, -\ln(2)) \).

Se \( y = 0 \), allora \( \ln\left(\frac{x+1}{x^2+2}\right) = 0 \), da cui \( \frac{x+1}{x^2+2} = e^0 = 1 \). Quindi \( x+1 = x^2+2 \), che implica \( x^2 - x + 1 = 0 \). Il discriminante di questa equazione quadratica è \( \Delta = (-1)^2 - 4(1)(1) = 1 - 4 = -3 < 0 \). Pertanto, non ci sono soluzioni reali per \( x \), e non ci sono intersezioni con l'asse x.

Segno della funzione:

Il segno di \( f(x) = \ln\left(\frac{x+1}{x^2+2}\right) \) dipende dal segno dell'argomento rispetto a 1.

• \( f(x) > 0 \) se \( \frac{x+1}{x^2+2} > 1 \implies x+1 > x^2+2 \implies x^2 - x + 1 < 0 \). Come visto prima, \( x^2 - x + 1 \) non ha radici reali e il suo coefficiente di \( x^2 \) è positivo, quindi è sempre positivo. Pertanto, \( f(x) \) non è mai positiva.
• \( f(x) < 0 \) se \( \frac{x+1}{x^2+2} < 1 \implies x+1 < x^2+2 \implies x^2 - x + 1 > 0 \). Questo è sempre vero per tutti gli \( x \in \mathbb{R} \). Considerando il dominio \( x > -1 \), la funzione è sempre negativa nel suo dominio.
• \( f(x) = 0 \) se \( \frac{x+1}{x^2+2} = 1 \), che non ha soluzioni reali.

Quindi la funzione è sempre negativa per \( x > -1 \).

Limiti:

• \( \lim_{x \to -1^+} \ln\left(\frac{x+1}{x^2+2}\right) \). Per \( x \to -1^+ \), \( x+1 \to 0^+ \), e \( x^2+2 \to 1+2 = 3 \). Quindi l'argomento del logaritmo tende a \( \frac{0^+}{3} = 0^+ \), e \( \ln(0^+) = -\infty \). La retta \( x = -1 \) è un asintoto verticale.
• \( \lim_{x \to +\infty} \ln\left(\frac{x+1}{x^2+2}\right) = \lim_{x \to +\infty} \ln\left(\frac{x}{x^2}\right) = \lim_{x \to +\infty} \ln\left(\frac{1}{x} \right) = \ln(0^+) = -\infty \).

Asintoti:

• Asintoto verticale: \( x = -1 \) poiché \( \lim_{x \to -1^+} f(x) = -\infty \).
• Asintoto orizzontale: Non c'è asintoto orizzontale poiché \( \lim_{x \to +\infty} f(x) = -\infty \).
• Asintoto obliquo: Verifichiamo se esiste un asintoto obliquo \( y = mx + q \). \[ m = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{\ln\left(\frac{x+1}{x^2+2}\right)}{x} \] Per \( x \to +\infty \), l'argomento del logaritmo \( \frac{x+1}{x^2+2} \) si comporta come \( \frac{x}{x^2} = \frac{1}{x} \). Quindi, \( \ln\left(\frac{x+1}{x^2+2}\right) \) si comporta come \( \ln\left(\frac{1}{x}\right) = -\ln(x) \). Pertanto, il limite per \( m \) diventa: \[ m = \lim_{x \to +\infty} \frac{-\ln(x)}{x} \] Questo limite è 0 poiché il denominatore \( x \) è un infinito di ordine superiore rispetto al numeratore \( \ln(x) \). Quindi non c'è asintoto obliquo.

Derivata prima:

\[ f'(x) = \frac{d}{dx} \left[ \ln\left(\frac{x+1}{x^2+2}\right) \right] = \frac{x^2+2}{x+1} \cdot \frac{(1)(x^2+2) - (x+1)(2x)}{(x^2+2)^2} = \frac{x^2+2 - 2x^2 - 2x}{(x+1)(x^2+2)} = \frac{-x^2 - 2x + 2}{(x+1)(x^2+2)} \]

Studiare il segno di \( f'(x) \) dipende dal segno del numeratore \( -x^2 - 2x + 2 \) (il denominatore è positivo per \( x > -1 \)). Le radici di \( -x^2 - 2x + 2 = 0 \) sono \( x = \frac{2 \pm \sqrt{4 - 4(-1)(2)}}{-2} = \frac{2 \pm \sqrt{12}}{-2} = \frac{2 \pm 2\sqrt{3}}{-2} = -1 \mp \sqrt{3} \). Le radici sono \( -1 - \sqrt{3} \approx -2.73 \) e \( -1 + \sqrt{3} \approx 0.73 \). Considerando il dominio \( x > -1 \), la derivata prima è positiva per \( -1 < x < -1 + \sqrt{3} \) e negativa per \( x > -1 + \sqrt{3} \). Quindi c'è un massimo relativo in \( x = -1 + \sqrt{3} \).

Derivata seconda:

Abbiamo la derivata prima: \( f'(x) = \frac{-x^2 - 2x + 2}{(x+1)(x^2+2)} = \frac{-x^2 - 2x + 2}{x^3 + x^2 + 2x + 2} \).

Applicando la regola del quoziente \( \left(\frac{u}{v}\right)' = \frac{u'v - uv'}{v^2} \) con \( u = -x^2 - 2x + 2 \) (\( u' = -2x - 2 \)) e \( v = x^3 + x^2 + 2x + 2 \) (\( v' = 3x^2 + 2x + 2 \)):

\[ f''(x) = \frac{(-2x - 2)(x^3 + x^2 + 2x + 2) - (-x^2 - 2x + 2)(3x^2 + 2x + 2)}{(x^3 + x^2 + 2x + 2)^2} \]

\[ = \frac{(-2x^4 - 2x^3 - 4x^2 - 4x - 2x^3 - 2x^2 - 4x - 4) - (-3x^4 - 2x^3 - 2x^2 - 6x^3 - 4x^2 - 4x + 6x^2 + 4x + 4)}{(x^3 + x^2 + 2x + 2)^2} \]

\[ = \frac{(-2x^4 - 4x^3 - 6x^2 - 8x - 4) - (-3x^4 - 8x^3 + 4)}{(x^3 + x^2 + 2x + 2)^2} \]

\[ = \frac{-2x^4 - 4x^3 - 6x^2 - 8x - 4 + 3x^4 + 8x^3 - 4}{(x^3 + x^2 + 2x + 2)^2} \]

\[ = \frac{x^4 + 4x^3 - 6x^2 - 8x - 8}{((x+1)(x^2+2))^2} = \frac{x^4 + 4x^3 - 6x^2 - 8x - 8}{(x+1)^2 (x^2+2)^2} \]

Il numeratore \( P(x) = x^4 + 4x^3 - 6x^2 - 8x - 8 \) si scompone, utilizzando la regola di Ruffini con la radice \( x = 2 \):

\[ \begin{array}{c|cccc|c} & 1 & 4 & -6 & -8 & -8 \\ 2 & & 2 & 12 & 12 & 8 \\ \hline & 1 & 6 & 6 & 4 & 0 \\ \end{array} \]

Quindi, \( x^4 + 4x^3 - 6x^2 - 8x - 8 = (x-2)(x^3+6x^2+6x+4) \). La derivata seconda diventa:

\[ f''(x) = \frac{(x-2)(x^3+6x^2+6x+4)}{(x+1)^2 (x^2+2)^2} \]

Studiamo il segno di \( a(x) = x^3+6x^2+6x+4 \).

Questa funzione è continua su tutto l’asse reale e taglia l’asse delle ordinate in \( y = 4 \).

Risulta: \( a'(x) = 3x^2+12x+6 \ge 0 \) se \( x^2+4x+2 \ge 0 \), cioè per \( x \le c_1 = -2-\sqrt{2} \approx -3.4 \) oppure \( x \ge c_2 = -2+\sqrt{2} \approx -0.6 \).

La funzione \( a(x) \) è quindi crescente da \( -\infty \) a circa \( -3.4 \), decrescente da circa \( -3.4 \) a circa \( -0.6 \) e crescente da circa \( -0.6 \) a \( +\infty \).

Quindi il grafico di \( a(x) \) ha un massimo relativo in \( x \approx -3.4 \) ed un minimo relativo in \( x \approx -0.6 \). L’ordinata del minimo è circa \( a(-0.6) \approx 2.3 \).

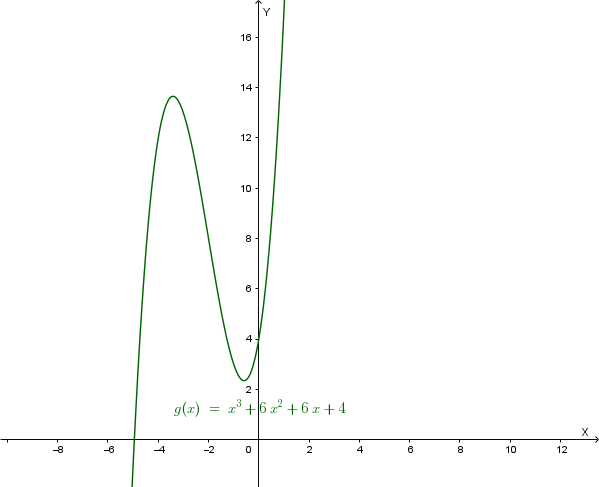
Dal grafico di \( a(x) \) deduciamo che \( x^3+6x^2+6x+4 \) è sempre positivo per \( x > -1 \). Pertanto risulta:

• \( f''(x) < 0 \) per \( x < 2 \) (concavità verso il basso)
• \( f''(x) > 0 \) per \( x > 2 \) (concavità verso l’alto)
• \( f''(x) = 0 \) per \( x = 2 \): punto di flesso. Il flesso ha coordinate \( F = (2, f(2)) \).

Calcoliamo l'ordinata del punto di flesso: \( f(2) = \ln\left(\frac{2+1}{2^2+2}\right) = \ln\left(\frac{3}{6}\right) = \ln\left(\frac{1}{2}\right) = -\ln(2) \).

Quindi il punto di flesso è \( F = (2, -\ln(2)) \).

Grafico della Funzione

Dominio

La funzione \( f(x) = 2 - \frac{1 + \ln(x)}{x} \) è definita quando il logaritmo è definito (\( x > 0 \)) e quando il denominatore non è nullo (\( x \neq 0 \)). Entrambe le condizioni ci portano a:

\[ \boxed{D = (0, +\infty)} \]

Parità

Per verificare se la funzione è pari o dispari, dobbiamo considerare il suo dominio. Poiché il dominio è \( (0, +\infty) \), che non è simmetrico rispetto all'origine, la funzione non può essere né pari né dispari.

Intersezioni con gli assi

Asse x (y=0):

\[ 2 - \frac{1 + \ln(x)}{x} = 0 \implies 2x - (1 + \ln(x)) = 0 \implies 2x - 1 - \ln(x) = 0 \implies \ln(x) = 2x - 1 \]

Questa equazione non ha soluzioni algebriche semplici. Possiamo analizzare graficamente l'intersezione tra \( y = \ln(x) \) e \( y = 2x - 1 \):

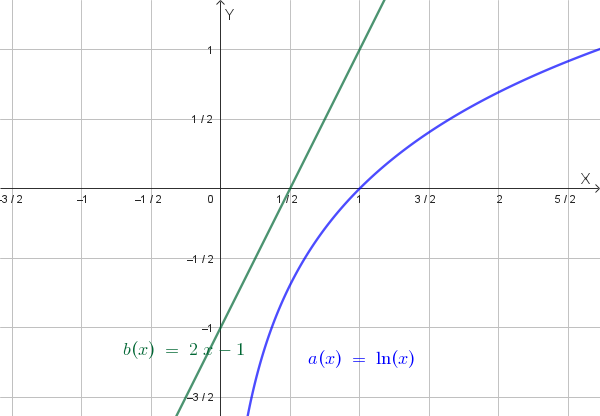
Il grafico evidenzia che non ci sono intersezioni, quindi la funzione non interseca l'asse x.

Asse y:

La funzione non è definita per \( x = 0 \), quindi non ci sono intersezioni con l'asse y.

Studio del Segno

Il segno della funzione \( f(x) = 2 - \frac{1 + \ln(x)}{x} = \frac{2x - 1 - \ln(x)}{x} \) dipende dal segno del numeratore \( 2x - 1 - \ln(x) \) (il denominatore \( x \) è positivo per \( x > 0 \)). Il numeratore è positivo se \( 2x - 1 > \ln(x) \).

Analizziamo graficamente la relazione tra \( y = \ln(x) \) e \( y = 2x - 1 \):

Il grafico evidenzia che la retta \( y = 2x - 1 \) si trova sempre al di sopra della curva \( y = \ln(x) \) per \( x > 0 \). Pertanto, \( 2x - 1 > \ln(x) \) è sempre verificato nel dominio della funzione.

Di conseguenza, il numeratore \( 2x - 1 - \ln(x) \) è sempre positivo per \( x > 0 \). Dato che anche il denominatore \( x \) è positivo per \( x > 0 \), la funzione \( f(x) \) è sempre positiva nel suo dominio:

\[ f(x) > 0 \quad \text{per } x \in (0, +\infty) \]

Studio dei Limiti

Per \( x \to 0^+ \):

\[ \lim_{x \to 0^+} \left(2 - \frac{1 + \ln(x)}{x}\right) = 2 - \frac{1 - \infty}{0^+} = 2 - (-\infty) = +\infty \]

La retta \( x = 0 \) è un asintoto verticale.

Per \( x \to +\infty \):

\[ \lim_{x \to +\infty} \left(2 - \frac{1 + \ln(x)}{x}\right) = 2 - \lim_{x \to +\infty} \frac{1}{x} - \lim_{x \to +\infty} \frac{\ln(x)}{x} = 2 - 0 - 0 = 2 \]

La retta \( y = 2 \) è un asintoto orizzontale per \( x \to +\infty \).

Ricerca degli Asintoti

• Asintoti Orizzontali: \( y = 2 \) per \( x \to +\infty \).
• Asintoti Verticali: \( x = 0 \) poiché \( \lim_{x \to 0^+} f(x) = +\infty \).
• Asintoti Obliqui: Poiché esiste un asintoto orizzontale per \( x \to +\infty \), non ci può essere un asintoto obliquo in quella direzione.

Derivata Prima

\[ f'(x) = \frac{d}{dx} \left(2 - \frac{1 + \ln(x)}{x}\right) = 0 - \frac{\frac{1}{x} \cdot x - (1 + \ln(x)) \cdot 1}{x^2} = - \frac{1 - 1 - \ln(x)}{x^2} = \frac{\ln(x)}{x^2} \]

Studio del segno di \( f'(x) \):

• \( f'(x) > 0 \) se \( \ln(x) > 0 \implies x > 1 \) (funzione crescente).
• \( f'(x) < 0 \) se \( \ln(x) < 0 \implies 0 < x < 1 \) (funzione decrescente).
• \( f'(x) = 0 \) se \( \ln(x) = 0 \implies x = 1 \) (punto stazionario).

In \( x = 1 \) c'è un minimo locale con valore \( f(1) = 2 - \frac{1 + \ln(1)}{1} = 2 - \frac{1 + 0}{1} = 1 \). Punto di minimo locale: \( (1, 1) \).

Derivata Seconda

\[ f''(x) = \frac{d}{dx} \left(\frac{\ln(x)}{x^2}\right) = \frac{\frac{1}{x} \cdot x^2 - \ln(x) \cdot 2x}{(x^2)^2} = \frac{x - 2x \ln(x)}{x^4} = \frac{1 - 2 \ln(x)}{x^3} \]

Studio del segno di \( f''(x) \):

• Il denominatore nel dominio è sempre positivo.
• \( f''(x) > 0 \) se \( 1 - 2 \ln(x) > 0 \implies \ln(x) < 1/2 \implies x < e^{1/2} = \sqrt{e} \approx 1.649 \) (concavità verso l'alto).
• \( f''(x) < 0 \) se \( 1 - 2 \ln(x) < 0 \implies \ln(x) > 1/2 \implies x > e^{1/2} = \sqrt{e} \approx 1.649 \) (concavità verso il basso).
• \( f''(x) = 0 \) se \( 1 - 2 \ln(x) = 0 \implies x = \sqrt{e} \) (punto di flesso).

Punto di flesso in \( x = \sqrt{e} \approx 1.649 \). L'ordinata del punto di flesso è \( f(\sqrt{e}) = 2 - \frac{1 + \ln(\sqrt{e})}{\sqrt{e}} = 2 - \frac{1 + 1/2}{\sqrt{e}} = 2 - \frac{3}{2\sqrt{e}} \approx 2 - \frac{3}{2 \cdot 1.649} \approx 2 - 0.91 = 1.09 \).

Grafico della Funzione