

Calcolo del volume di un solido per sezioni
- Premi il bottone "Teoria Volumi Sezione" per la spiegazione teorica.
- Premi il bottone "Test versione standard" per il test con soluzioni guidate.
- Premi il bottone "Test versione DSA" per la versione ad alta leggibilità.
Spiegazione Teorica
Volume di un solido con sezioni perpendicolari all'asse x o y
Quando si desidera calcolare il volume di un solido che ha per base una regione \( R \) del piano cartesiano e sezioni trasversali perpendicolari all'asse \( x \) o \( y \), si può utilizzare il metodo delle sezioni trasversali.
Metodo delle Sezioni Trasversali
Questo metodo è utile quando le sezioni trasversali del solido sono tutte simili e la loro area può essere espressa come una funzione della variabile di integrazione, che può essere \( x \) o \( y \), a seconda dell'orientamento delle sezioni.
Sezioni Perpendicolari all'Asse \( x \)
Supponiamo che la regione \( R \) sia delimitata dalle curve \( y = f(x) \) e \( y = g(x) \) sull'intervallo \( [a, b] \):
- Ogni sezione trasversale perpendicolare all'asse \( x \) ha un'area \( A(x) \) che varia in funzione di \( x \).
- Il volume \( V \) del solido è dato dall'integrale dell'area delle sezioni trasversali lungo l'intervallo \( [a, b] \):
Sezioni Perpendicolari all'Asse \( y \)
Supponiamo che la regione \( R \) sia delimitata dalle curve \( x = h(y) \) e \( x = k(y) \) sull'intervallo \( [c, d] \):
- Ogni sezione trasversale perpendicolare all'asse \( y \) ha un'area \( A(y) \) che varia in funzione di \( y \).
- Il volume \( V \) del solido è dato dall'integrale dell'area delle sezioni trasversali lungo l'intervallo \( [c, d] \):
Esempio 1: Sezioni perpendicolari all'asse x
Consideriamo un solido con base \( R \) delimitata da \( y = \sqrt{x} \), l'asse x e la retta \( x = 4 \). Ogni sezione trasversale è un quadrato con lato \( \sqrt{x} \).
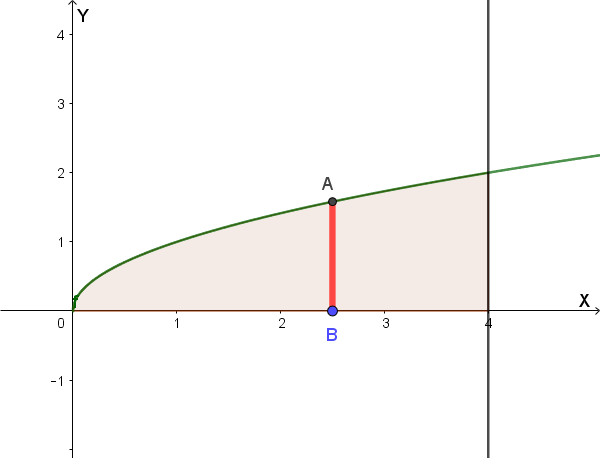
L'area della sezione trasversale è:
Il volume del solido è:
Esempio 2: Sezioni perpendicolari all'asse y
Consideriamo un solido con base \( R \) delimitata da \( y = x^2 \) e la retta \( y = 4 \). Ogni sezione trasversale è un semicerchio con diametro \( AB \), dove \( A \) e \( B \) sono le intersezioni con la parabola.
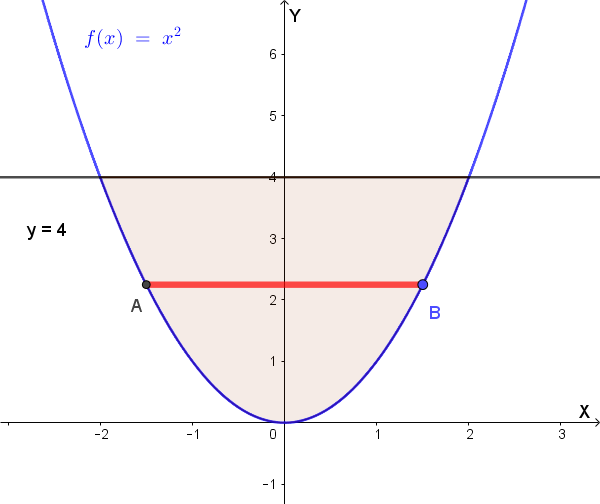
Per un dato valore di \( y \), il piano perpendicolare all'asse \( y \) interseca la parabola \( y = x^2 \) nei punti \( A = (-\sqrt{y}, y) \) e \( B = (\sqrt{y}, y) \). La distanza tra questi due punti, che rappresenta il diametro del semicerchio, è:
Pertanto, il raggio del semicerchio è la metà del diametro:
L'area della sezione trasversale è:
Il volume del solido è:
Esempio 3: Sezioni Perpendicolari all'Asse \( x \)
Consideriamo la regione compresa tra \( f(x) = x^2 - 3x + 2 \), \( g(x) = x^2 - x \) e l'asse delle \( y \). Ogni sezione trasversale è un triangolo equilatero.
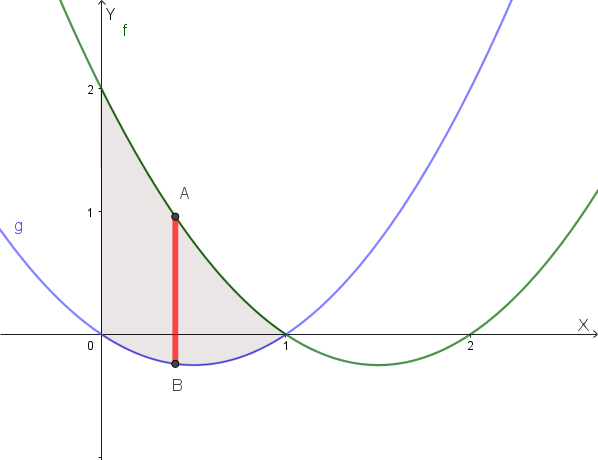
La regione \( R \) è delimitata da:
- \( f(x) = x^2 - 3x + 2 \) e \( g(x) = x^2 - x \) tra \( x = 0 \) e \( x = 1 \).
- L'asse delle \( y \) rappresenta il confine sinistro della regione.
Ogni sezione trasversale perpendicolare all'asse \( x \) è un triangolo equilatero. Indichiamo con \( A \) l'intersezione della sezione con \( f(x) \) e con \( B \) l'intersezione della sezione con \( g(x) \).
Il lato \( AB \) del triangolo equilatero è dato dalla differenza tra \( f(x) \) e \( g(x) \):
L'area di un triangolo equilatero di lato \( l \) è data dalla formula:
Quindi, l'area \( A(x) \) del triangolo equilatero è:
Il volume \( V \) del solido è dato dall'integrale dell'area delle sezioni trasversali lungo l'intervallo \([0, 1]\):
Sviluppiamo i calcoli dell'integrale:
Determiniamo la primitiva di \( 1 - 2x + x^2 \):
Valutiamo la primitiva agli estremi \( x = 1 \) e \( x = 0 \):
Quindi, il valore dell'integrale è:
E il volume del solido è: