



Quando una regione piana ruota attorno a una retta (ad esempio l'asse x o y), genera un solido tridimensionale. Possiamo calcolare il volume di questo solido con due metodi principali:
Utile quando la regione ruota attorno all'asse x o a una retta orizzontale (parallela all'asse x).
Formula generale (rotazione attorno all'asse x):
V = π ∫ab [f(x)]² dx
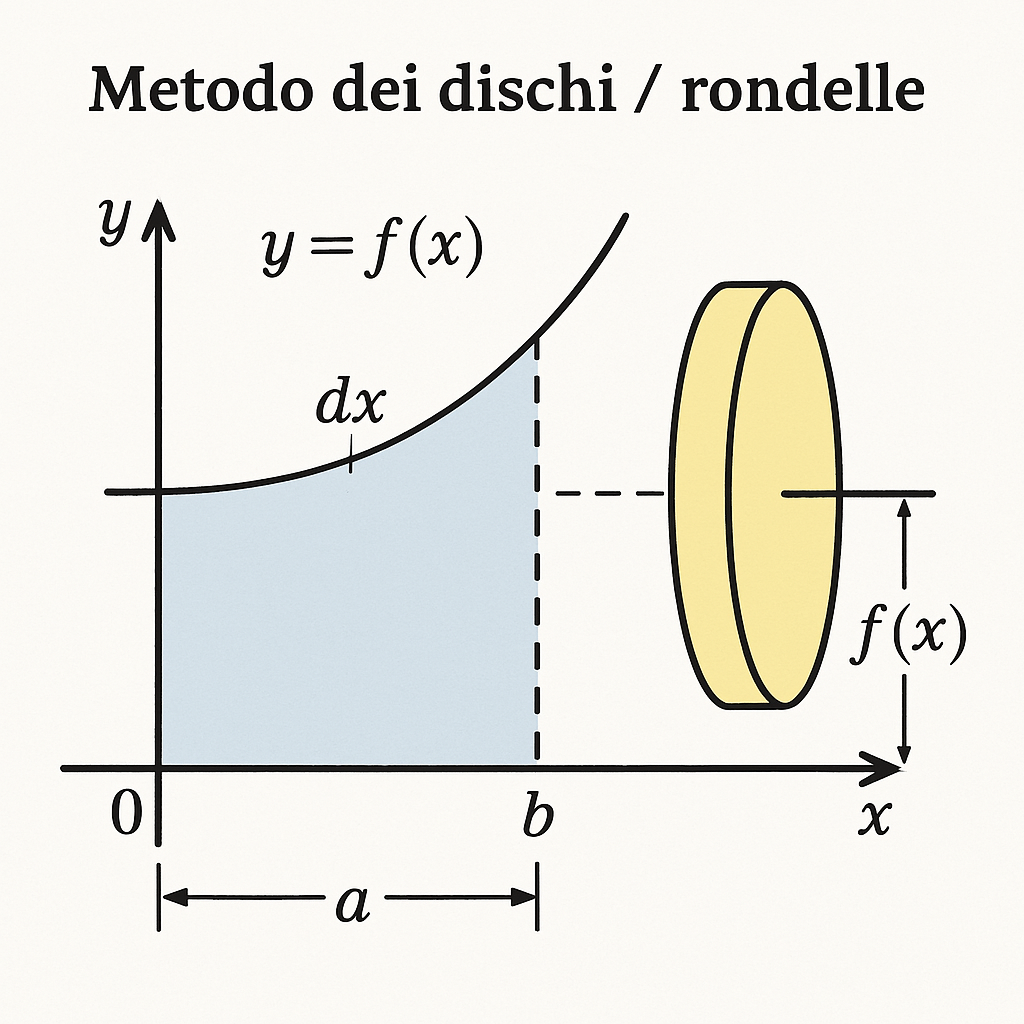
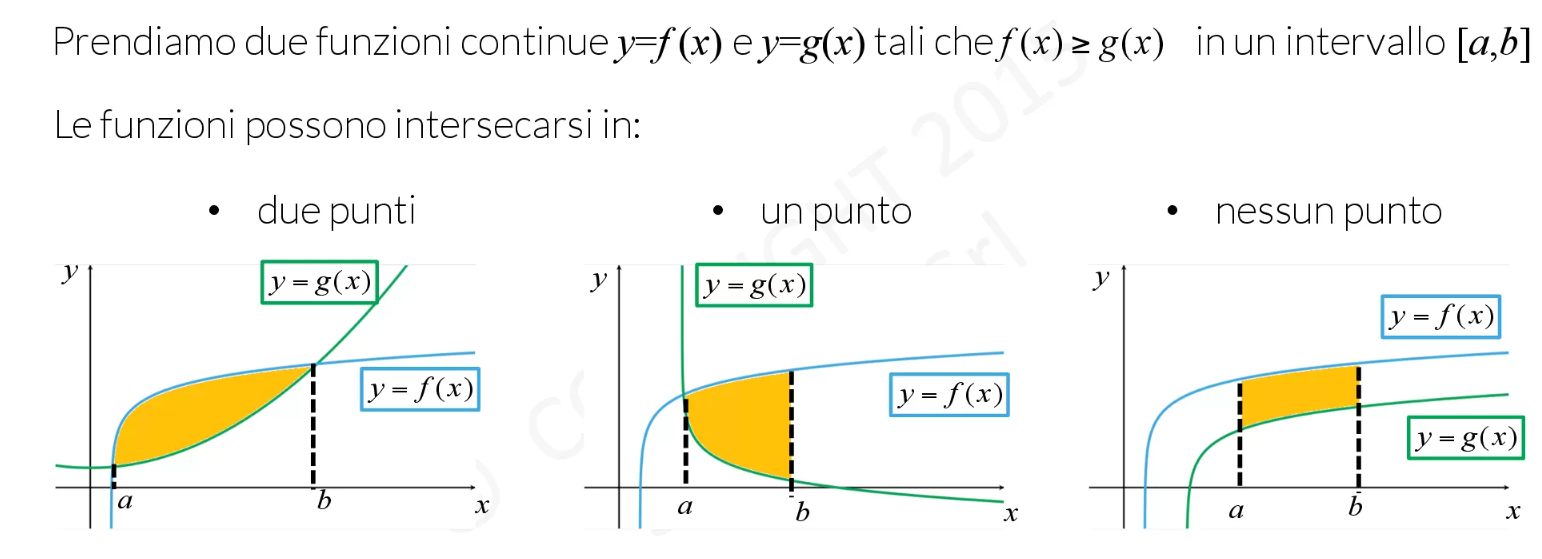
Se la regione è compresa tra due funzioni (f sopra, g sotto):
V = π ∫ab ([f(x)]² - [g(x)]²) dx
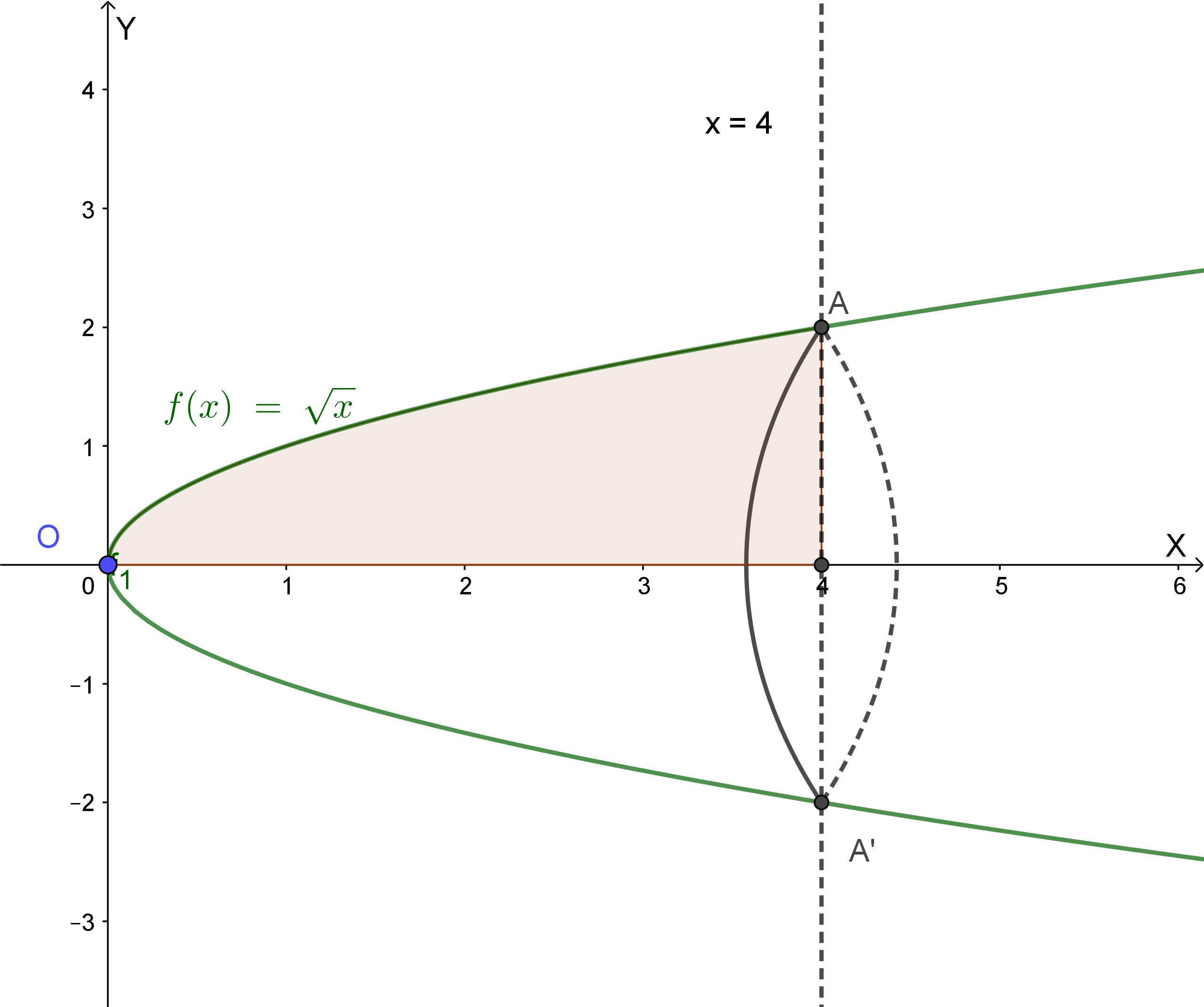
Trova il volume del solido generato dalla rotazione della regione delimitata da y = √x, l'asse x e le rette x = 0 e x = 4 attorno all'asse x.
Formula:
V = π ∫04 (√x)² dx = π ∫04 x dx = π [x²/2]04 = π(16/2) = 8π
Calcolo di volumi per rotazioni attorno all'asse y
Concetto Base
Il metodo dei gusci cilindrici (o shell method) è una tecnica per calcolare il volume di un solido di rotazione quando la regione piana ruota attorno a un asse verticale (come l'asse y o una retta x = k).
Se ruotiamo un'area sotto una curva \( y = f(x) \) tra \( x = a \) e \( x = b \) attorno all'asse y, il solido risultante può essere scomposto in tanti gusci cilindrici concentrici.
Ogni guscio ha:
Il volume del solido è dato da:
Problema: Calcolare il volume generato ruotando la regione sotto \( y = \sqrt{x} \) tra \( x = 0 \) e \( x = 4 \) attorno all'asse y.
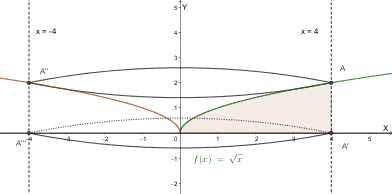
Risultato Finale:
\[ V = \frac{128}{5} \pi \quad \text{(unità di volume)} \]| Metodo | Asse di Rotazione | Formula |
|---|---|---|
| Gusci Cilindrici | Asse verticale (es. y) | \( V = 2\pi \int x \cdot f(x) \, dx \) |
| Dischi/Rondelle | Asse orizzontale (es. x) | \( V = \pi \int f(x)^2 \, dx \) |
Muovi il cursore per vedere come varia lo spessore del guscio:
Quando ruotiamo una regione attorno a una retta parallela agli assi ma non coincidente con essi, dobbiamo considerare la distanza tra la funzione e l'asse di rotazione. Questo influisce sul raggio dei dischi o dei gusci utilizzati nel calcolo.
y = c (retta orizzontale)Metodo dei dischi (o rondelle)
Quando ruotiamo attorno alla retta orizzontale y = c:
r(x) = |f(x) - c|
dV = π[f(x) - c]² dx
V = π ∫ab [f(x) - c]² dx
Calcolare il volume del solido generato ruotando la regione delimitata da y = x², y = 0, x = 1 attorno alla retta y = -1.
Soluzione:
r(x) = x² - (-1) = x² + 1
V = π ∫01 (x² + 1)² dx = π ∫01 (x⁴ + 2x² + 1) dx = π [x⁵/5 + (2x³)/3 + x]01 = π (1/5 + 2/3 + 1) = 28π/15
x = k (retta verticale)Metodo dei gusci cilindrici
Quando ruotiamo attorno alla retta verticale x = k:
r(x) = |x - k|
dV = 2π|x - k|f(x) dx
V = 2π ∫ab |x - k| f(x) dx
Calcolare il volume del solido generato ruotando la regione delimitata da y = √x, y = 0, x = 4 attorno alla retta x = -2.
Soluzione:
r(x) = x - (-2) = x + 2(poiché x ≥ 0 > -2, il valore assoluto è positivo)
V = 2π ∫04 (x + 2)√x dx = 2π ∫04 (x3/2 + 2x1/2) dx = 2π [(2/5)x5/2 + (4/3)x3/2]04 = 2π [(2/5)32 + (4/3)8] = 2π [64/5 + 32/3] = 896π/15