Compito in Classe di Matematica

Soluzione Esercizio 1

Analisi delle tre funzioni:

Per x < 0: f(x) = e^x

Si tratta di una funzione esponenziale con base e (numero di Nepero). Questa funzione è sempre positiva, crescente e ha asintoto orizzontale y = 0 per x → -∞. Nel punto x = 0 avremmo f(0) = e⁰ = 1, ma questo punto non appartiene al dominio di questa parte della funzione.

Per 0 ≤ x < 5: f(x) = (1/3)x² - (4/3)x + 1

Si tratta di una parabola con concavità verso l'alto (a = 1/3 > 0). Per trovare il vertice:

x_v = -b/(2a) = -(-4/3)/(2·1/3) = (4/3)/(2/3) = 2

y_v = f(2) = (1/3)·4 - (4/3)·2 + 1 = 4/3 - 8/3 + 1 = -4/3 + 1 = -1/3

Il vertice è V(2, -1/3). La parabola interseca l'asse y in f(0) = 1.

Il punto B della parabola (che non fa parte del grafico di f) di ascissa 5 ha ordinata 8/3. Questo valore servirà per la discussione successiva.

Per 5 ≤ x ≤ 47/7: f(x) = -x + 7

Si tratta di una retta con coefficiente angolare m = -1 (decrescente) e intercetta q = 7. Il dominio di questa parte va da x = 5 a x = 47/7 ≈ 6.71.

f(5) = -5 + 7 = 2

f(47/7) = -47/7 + 7 = -47/7 + 49/7 = 2/7

Il grafico della funzione è quindi il seguente:

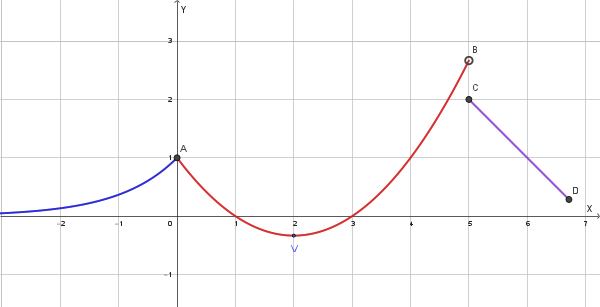
Dal grafico deduciamo:

Estremo superiore: 8/3.

Estremo inferiore: Il minimo valore è raggiunto nel vertice della parabola: inf f = -1/3.

Oscillazione: osc f = sup f - inf f =8/3-(-1/3)=3.

Massimi e minimi (della funzione):

• Minimo assoluto: -1/3 (nel vertice della parabola)
• Massimo assoluto: Non esiste
• Minimi relativi: -1/3 e 2/7
• Massimi relativi: 0

Intersezioni con rette parallele all'asse x (y = k):

Nel seguente grafico indichiamo le rette caratteristiche per la discussione:

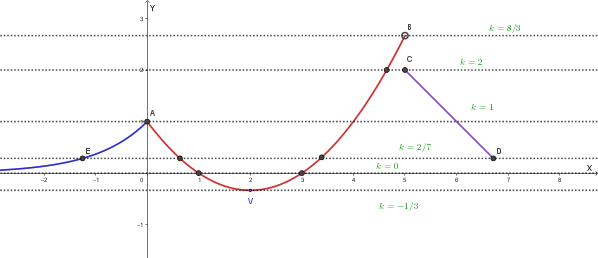
Il numero di intersezioni dipende dal valore di k:

• Se k < -1/3: nessuna intersezione
• Se k = -1/3: una sola intersezione (nel vertice x = 2)
• Se -1/3 < k < 0: due intersezioni (sulla parabola)
• Se k = 0: due intersezioni (sulla parabola)
• Se 0 < k < 2/7: tre intersezioni (una sul ramo esponenziale, due sulla parabola)
• Se k = 2/7: quattro intersezioni (esponenziale, due con parabola, retta)
• Se 2/7 < k < 1: quattro intersezioni (esponenziale, due con la parabola, retta)
• Se k = 1: tre intersezioni (parabola nel punto x = 0 ed in altro punto e retta)
• Se 1 < k < 2: due intersezioni (parabola e retta)
• Se k = 2: due intersezioni (parabola e retta nel punto x = 5)
• Se 2 < k < 8/3: una intersezione (parabola)
• Se k ≥ 8/3: nessuna intersezione

Soluzione Esercizio 2

Dominio:

Per determinare il dominio della funzione, dobbiamo imporre le seguenti condizioni:

1. L'argomento della radice quadrata deve essere non negativo: \( x^2 - 1 \ge 0 \)
2. L'argomento del logaritmo deve essere positivo: \( \frac{x}{x^2 - 4} > 0 \)
3. Il denominatore della frazione deve essere diverso da zero: \( \ln\left(\frac{x}{x^2 - 4}\right) \neq 0 \)

Analisi della prima condizione: \( x^2 - 1 \ge 0 \)

Questa disequazione è soddisfatta per \( x \le -1 \) o \( x \ge 1 \).

Analisi della seconda condizione: \( \frac{x}{x^2 - 4} > 0 \)

• Numeratore: \( x > 0 \)
• Denominatore: \( x^2 - 4 > 0 \implies x < -2 \) o \( x > 2 \)

Combinando i segni, la frazione è positiva per \( x \in (-2, 0) \cup (2, +\infty) \).

Analisi della terza condizione: \( \ln\left(\frac{x}{x^2 - 4}\right) \neq 0 \)

Questo accade quando l'argomento del logaritmo è diverso da 1:

\(\frac{x}{x^2 - 4} \neq 1 \implies x \neq x^2 - 4 \implies x^2 - x - 4 \neq 0 \)

Le radici di \(x^2 - x - 4 = 0\) sono: \(x = \frac{1 \pm \sqrt{1 - 4(1)(-4)}}{2} = \frac{1 \pm \sqrt{17}}{2}\).

Quindi \(x \neq \frac{1 + \sqrt{17}}{2}\) e \(x \neq \frac{1 - \sqrt{17}}{2}\).

Intersezione dei domini:

Il dominio finale è l'intersezione delle tre condizioni, escludendo i punti specifici trovati:

\(D = ((-2, 0) \cup (2, +\infty)) \cap ((-\infty, -1] \cup [1, +\infty)) - \left\{ \frac{1 \pm \sqrt{17}}{2} \right\}\)

Il dominio è: \(D = (-2, -1] \cup (2, +\infty)\), escludendo i valori specifici di \(x\) \(\frac{1 - \sqrt{17}}{2}\) e \(\frac{1 + \sqrt{17}}{2}\), che appartengono a questi intervalli.

Intersezioni con gli assi:

• Asse y (x=0): Il punto \(x=0\) non appartiene al dominio, quindi non ci sono intersezioni con l'asse y.
• Asse x (y=0): La frazione è nulla solo se il numeratore è nullo, ovvero \( \sqrt{x^2 - 1} = 0 \). Questo accade per \( x^2 - 1 = 0 \implies x = \pm 1 \). Solo \(x=-1\) appartiene al dominio.
  Il punto di intersezione è \((-1, 0)\).

Segno della funzione:

La frazione ha segno positivo quando numeratore e denominatore hanno lo stesso segno.

• Numeratore: \(N(x) = \sqrt{x^2 - 1}\). È sempre non negativo nel suo dominio. Quindi \(N(x) \ge 0\) in \((-\infty, -1] \cup [1, +\infty)\) e \(N(x) > 0\) in \(x \in (-\infty, -1) \cup (1, +\infty)\).
• Denominatore: \(D(x) = \ln\left(\frac{x}{x^2 - 4}\right)\). Il logaritmo è positivo quando il suo argomento è maggiore di 1, ed è negativo quando è compreso tra 0 e 1.
  \( \frac{x}{x^2 - 4} > 1 \implies \frac{x - (x^2 - 4)}{x^2 - 4} > 0 \implies \frac{-x^2 + x + 4}{x^2 - 4} > 0 \implies \frac{x^2 - x - 4}{x^2 - 4} < 0 \).
  

Dettaglio del calcolo del segno del denominatore

Il segno del denominatore \(D(x) = \ln\left(\frac{x}{x^2 - 4}\right)\) dipende dal segno dell'argomento della frazione \(\frac{x}{x^2 - 4}\) rispetto a 1.

La condizione \(D(x) > 0\) si verifica quando l'argomento del logaritmo è maggiore di 1:

\[\frac{x}{x^2 - 4} > 1 \implies \frac{x}{x^2 - 4} - 1 > 0 \implies \frac{x - (x^2 - 4)}{x^2 - 4} > 0 \implies \frac{-x^2 + x + 4}{x^2 - 4} > 0\]

Per facilitare la risoluzione, moltiplichiamo per -1 e invertiamo il segno della disequazione:

\[\frac{x^2 - x - 4}{x^2 - 4} < 0\]

Ora analizziamo il segno del numeratore e del denominatore di questa nuova frazione.

1. Segno del numeratore: \(x^2 - x - 4\)

Calcoliamo le radici dell'equazione \(x^2 - x - 4 = 0\):

\[x = \frac{1 \pm \sqrt{(-1)^2 - 4(1)(-4)}}{2} = \frac{1 \pm \sqrt{1 + 16}}{2} = \frac{1 \pm \sqrt{17}}{2}\]

Quindi il numeratore è positivo per valori esterni alle radici:

• \(x < \frac{1 - \sqrt{17}}{2}\)
• \(x > \frac{1 + \sqrt{17}}{2}\)

2. Segno del denominatore: \(x^2 - 4\)

Le radici dell'equazione \(x^2 - 4 = 0\) sono \(x = \pm 2\). Il denominatore è positivo per valori esterni alle radici:

• \(x < -2\)
• \(x > 2\)

3. Schema grafico dei segni

Ora combiniamo i segni del numeratore e del denominatore sul nostro schema. I valori approssimativi delle radici sono \(\frac{1 - \sqrt{17}}{2} \approx -1.56\) e \(\frac{1 + \sqrt{17}}{2} \approx 2.56\).

Schema grafico dei segni

Ecco uno schema che riassume il segno del numeratore e del denominatore, per determinare il segno della frazione.

Intervallo	\(x^2 - x - 4\) (Numeratore)	\(x^2 - 4\) (Denominatore)	\(\frac{x^2 - x - 4}{x^2 - 4}\) (Frazione)
\(x < -2\)	+	+	+
\(x = -2\)	+	0	Non definita
\(-2 < x < \frac{1 - \sqrt{17}}{2}\)	+	-	-
\(x = \frac{1 - \sqrt{17}}{2}\)	0	-	0
\(\frac{1 - \sqrt{17}}{2} < x < 2\)	-	-	+
\(x = 2\)	-	0	Non definita
\(2 < x < \frac{1 + \sqrt{17}}{2}\)	-	+	-
\(x = \frac{1 + \sqrt{17}}{2}\)	0	+	0
\(x > \frac{1 + \sqrt{17}}{2}\)	+	+	+

L'obiettivo è trovare gli intervalli in cui la frazione è minore di zero (\( < 0 \)). Dalla tabella, vediamo che ciò si verifica quando i segni sono discordi, ovvero negli intervalli:

\[x \in \left(-2, \frac{1 - \sqrt{17}}{2}\right) \cup \left(2, \frac{1 + \sqrt{17}}{2}\right)\]

Come puoi vedere dallo schema, la frazione \(\frac{x^2 - x - 4}{x^2 - 4}\) è minore di zero negli intervalli in cui i segni sono discordi:

\[x \in \left(-2, \frac{1 - \sqrt{17}}{2}\right) \cup \left(2, \frac{1 + \sqrt{17}}{2}\right)\]

Questo risultato ci dice che il denominatore originale della funzione, \(D(x) = \ln\left(\frac{x}{x^2 - 4}\right)\), è positivo per questi valori di \(x\).

Combinando il segno del numeratore (che è sempre non negativo nel dominio) con il segno del denominatore, otteniamo che il segno della funzione \(f(x)\) è determinato esclusivamente dal segno del denominatore.

Come abbiamo visto dallo schema dei segni, il denominatore è positivo quando \(x \in \left(-2, \frac{1 - \sqrt{17}}{2}\right) \cup \left(2, \frac{1 + \sqrt{17}}{2}\right)\).

• \(f(x) > 0\) per \(x \in \left(-2, \frac{1 - \sqrt{17}}{2}\right) \cup \left(2, \frac{1 + \sqrt{17}}{2}\right)\)

Il denominatore è negativo quando \(x \in \left(\frac{1 - \sqrt{17}}{2}, -1\right] \cup \left(\frac{1 + \sqrt{17}}{2}, +\infty\right)\).

• \(f(x) < 0\) per \(x \in \left(\frac{1 - \sqrt{17}}{2}, -1\right] \cup \left(\frac{1 + \sqrt{17}}{2}, +\infty\right)\)

Note: I valori \(x = -1\) e \(x = 1\) non sono inclusi negli intervalli perché in quei punti il numeratore è zero e l'intersezione con l'asse x è già stata calcolata.

Soluzione Esercizio 3

Analisi della funzione \(y=f(x)\):

La funzione data è una parabola con equazione \( y=f(x)=\frac{2}{5}x^2-\frac{8}{5}x-2 \). Poiché il coefficiente del termine quadratico (\(a = \frac{2}{5}\)) è positivo, la concavità della parabola è rivolta verso l'alto.

Per tracciare il grafico, troviamo il vertice e le intersezioni con gli assi.

1. Vertice

L'ascissa del vertice si calcola con la formula \( x_v = -\frac{b}{2a} \):

\( x_v = -\frac{-\frac{8}{5}}{2 \cdot \frac{2}{5}} = -\frac{-\frac{8}{5}}{\frac{4}{5}} = -(-\frac{8}{5} \cdot \frac{5}{4}) = \frac{8}{4} = 2 \)

L'ordinata del vertice si trova sostituendo \(x_v=2\) nella funzione:

\( y_v = f(2) = \frac{2}{5}(2)^2 - \frac{8}{5}(2) - 2 = \frac{8}{5} - \frac{16}{5} - \frac{10}{5} = -\frac{18}{5} \)

Il vertice è nel punto \( V\left(2, -\frac{18}{5}\right) \).

2. Intersezioni con gli assi

• Asse y (x=0): Sostituiamo \(x=0\) nella funzione: \( f(0) = -2 \). L'intersezione è nel punto \((0, -2)\).
• Asse x (y=0): Poniamo \(y=0\) e risolviamo l'equazione di secondo grado: \( 2x^2 - 8x - 10 = 0 \implies x^2 - 4x - 5 = 0 \). Le soluzioni sono \( x = -1 \) e \( x = 5 \). Le intersezioni sono nei punti \((-1, 0)\) e \((5, 0)\).

Il grafico della funzione \(y=f(x)\) è il seguente:

---

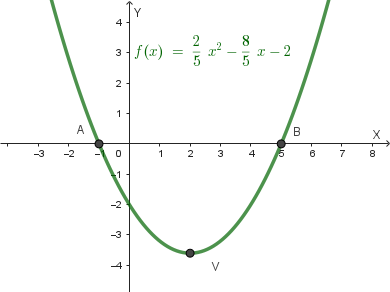
Analisi della funzione \(y=a(x)=-f(x)\):

La funzione \(y = a(x) = -f(x)\) si ottiene riflettendo il grafico della funzione originale \(f(x)\) rispetto all'asse delle ascisse (asse x). Questo significa che ogni punto \((x, y)\) sul grafico di \(f(x)\) si sposta nel punto \((x, -y)\) sul grafico di \(a(x)\). Ad esempio, il vertice di \(f(x)\) che era in \( V\left(2, -\frac{18}{5}\right) \), nel grafico di \(a(x)\) si troverà in \( V'\left(2, \frac{18}{5}\right) \).

Il suo grafico è il seguente:

---

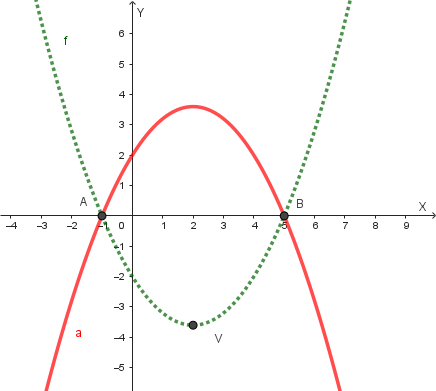
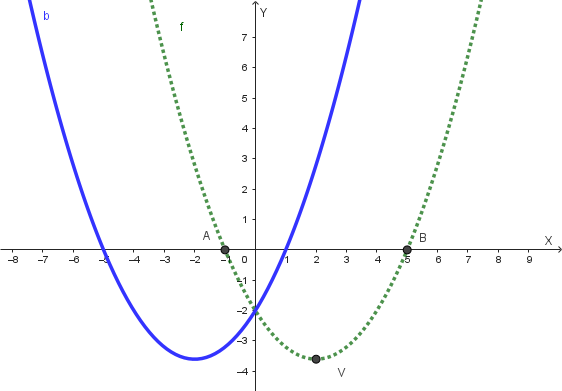
Analisi della funzione \(y=b(x)=f(-x)\):

Questa funzione si ottiene riflettendo il grafico della funzione originale \(f(x)\) rispetto all'asse delle ordinate (asse y). Ciò significa che ogni punto \((x, y)\) sul grafico di \(f(x)\) si sposta nel punto \((-x, y)\) sul grafico di \(b(x)\). Ad esempio, il vertice di \(f(x)\) che era in \(V\left(2, -\frac{18}{5}\right)\), nel grafico di \(b(x)\) si troverà in \(V''\left(-2, -\frac{18}{5}\right)\).

L'equazione di \(b(x)\) si ottiene sostituendo \(x\) con \(-x\) nell'espressione di \(f(x)\):

\( y=b(x)=f(-x)=\frac{2}{5}(-x)^2-\frac{8}{5}(-x)-2 = \frac{2}{5}x^2+\frac{8}{5}x-2 \)

Il grafico della funzione \(y=b(x)\) è il seguente:

---

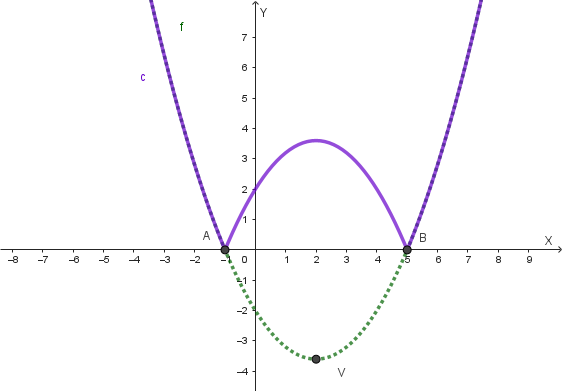
Analisi della funzione \(y=c(x)=|f(x)|\):

Questa funzione si ottiene riflettendo rispetto all'asse x tutte le parti del grafico di \(f(x)\) che si trovano al di sotto dell'asse x. Le parti del grafico che si trovano al di sopra o sull'asse x rimangono invariate.

L'equazione di \(c(x)\) è definita in due modi, a seconda del valore di \(f(x)\):

• \(c(x) = f(x)\) se \(f(x) \geq 0\) (ovvero, per \(x \leq -1\) o \(x \geq 5\))
• \(c(x) = -f(x)\) se \(f(x) < 0\) (ovvero, per \(-1 < x < 5\))

Il grafico della funzione \(y=c(x)=|f(x)|\) è il seguente:

---

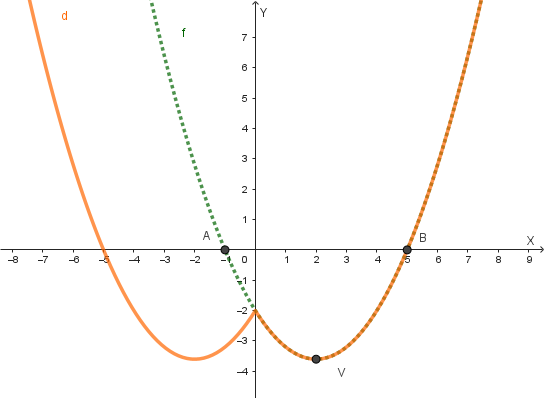
Analisi della funzione \(y=d(x)=f(|x|)\):

Questa funzione si ottiene mantenendo la parte del grafico di \(f(x)\) che si trova a destra dell'asse y (\(x \geq 0\)) e riflettendo tale parte rispetto all'asse y. La parte del grafico originale a sinistra dell'asse y (\(x < 0\)) viene eliminata.

L'equazione di \(d(x)\) si ottiene sostituendo \(x\) con \(|x|\) nell'espressione di \(f(x)\):

\( y=d(x)=f(|x|)=\frac{2}{5}|x|^2-\frac{8}{5}|x|-2 \)

Poiché \(|x|^2 = x^2\), l'equazione diventa:

\( y=d(x)=\frac{2}{5}x^2-\frac{8}{5}|x|-2 \)

Il grafico della funzione \(y=d(x)\) è il seguente:

---

Calcolo dell'area della regione finita di piano compresa fra il grafico di f e quello di a.

Rappresentiamo graficamente la regione compresa fra i grafici di \(y=f(x)\) ed \(y=a(x)=-f(x)\):

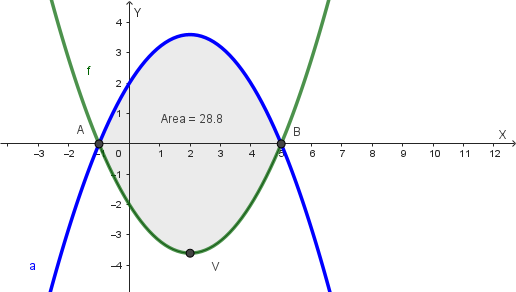
L'area richiesta è il doppio dell'area del segmento parabolico di base AB, con A=(-1,0) e B=(5,0) e altezza uguale al valore assoluto dell'ordinata del vertice V della parabola \(y=f(x)\).

Questo segmento parabolico, per il Teorema di Archimede, è uguale a \(\frac{2}{3}\) del rettangolo che ha per lati la base e l'altezza del segmento parabolico. L'area del segmento parabolico è quindi:

\( \text{Area}_{\text{segmento}} = \frac{2}{3} \cdot \text{base} \cdot \text{altezza} \)

La lunghezza della base è la distanza tra i punti di intersezione con l'asse x, ovvero \( |5 - (-1)| = 6 \).

L'altezza è il valore assoluto dell'ordinata del vertice, \( |y_v| = |-\frac{18}{5}| = \frac{18}{5} \).

Quindi l'area del segmento è:

\( \text{Area}_{\text{segmento}} = \frac{2}{3} \cdot 6 \cdot \frac{18}{5} = \frac{2}{3} \cdot \frac{108}{5} = \frac{216}{15} = \frac{72}{5} \)

L'area richiesta è il doppio di questa, quindi:

\( \text{Area}_{\text{totale}} = 2 \cdot \frac{72}{5} = \frac{144}{5} \)

Soluzione Esercizio 4

Soluzione punto a

- Il **dominio** della funzione \(f(x)\) è tutto R.
- Il **dominio** della funzione \(g(x)\) è \(x \ge 2\).

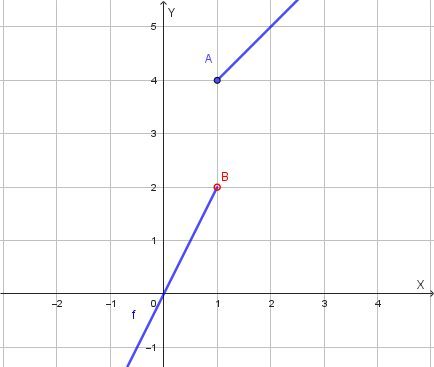
Il grafico di \(f(x)\) è formato da due rette:
- \(y = x+3\) se \(x \ge 1\)
- \(y = 2x\) se \(x < 1\)

Ecco il grafico della funzione \(f(x)\):

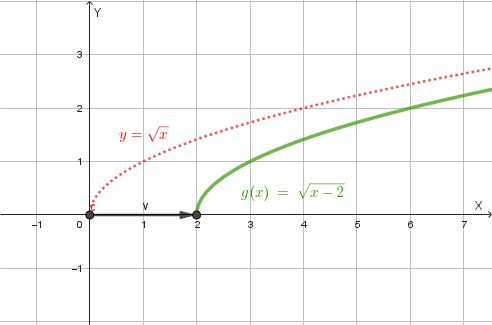
Il grafico della funzione \(g(x)\) si ottiene traslando il grafico di \(y = \sqrt{x}\) di 2 unità verso destra.

Ecco il grafico della funzione \(g(x)\):

Soluzione punto b

La funzione composta \(f \circ g\) è definita come \(f(g(x))\). Dato che la funzione \(f(x)\) ha due casi, dobbiamo valutarli entrambi:

• Caso 1: Se \(g(x) \ge 1\) \[ f(g(x)) = g(x) + 3 = \sqrt{x-2} + 3 \] Per trovare il dominio di questo caso, risolviamo la disequazione \(g(x) \ge 1\): \[ \sqrt{x-2} \ge 1 \implies x-2 \ge 1 \implies x \ge 3 \]
• Caso 2: Se \(g(x) < 1\) \[ f(g(x)) = 2g(x) = 2\sqrt{x-2} \] Per trovare il dominio di questo caso, risolviamo la disequazione \(g(x) < 1\): \[ \sqrt{x-2} < 1 \implies 0 \le x-2 < 1 \implies 2 \le x < 3 \]

Unendo i due casi, la funzione composta \(f \circ g\) è: \[ (f \circ g)(x) = \begin{cases} \sqrt{x-2} + 3 & \text{se } x \ge 3 \\ 2\sqrt{x-2} & \text{se } 2 \le x < 3 \end{cases} \]

Il **dominio** di \(f \circ g\) è l'unione dei domini dei due casi, che è \([2, +\infty)\).

Soluzione punto c

La funzione composta \(g \circ f\) è definita come \(g(f(x))\). Il dominio di \(g(x)\) è \(x \ge 2\), quindi dobbiamo assicurarci che \(f(x) \ge 2\).

• Caso 1: Se \(x \ge 1\) \[ g(f(x)) = g(x+3) = \sqrt{(x+3)-2} = \sqrt{x+1} \] Per trovare il dominio di questo caso, consideriamo due condizioni: \(x \ge 1\) (dalla definizione di \(f(x)\)) e \(f(x) \ge 2\). Risolviamo la disequazione \(x+3 \ge 2 \implies x \ge -1\). Intersecando le due condizioni (\(x \ge 1\) e \(x \ge -1\)) otteniamo \(x \ge 1\).
• Caso 2: Se \(x < 1\) \[ g(f(x)) = g(2x) = \sqrt{2x-2} \] Per trovare il dominio di questo caso, consideriamo due condizioni: \(x < 1\) (dalla definizione di \(f(x)\)) e \(f(x) \ge 2\). Risolviamo la disequazione \(2x \ge 2 \implies x \ge 1\). Intersecando le due condizioni (\(x < 1\) e \(x \ge 1\)) otteniamo un insieme vuoto. Questo significa che per questo caso non ci sono valori di \(x\) che soddisfano le condizioni.

La funzione composta \(g \circ f\) è definita solo nel primo caso: \[ (g \circ f)(x) = \sqrt{x+1} \quad \text{se } x \ge 1 \]

Il **dominio** di \(g \circ f\) è \([1, +\infty)\).