



Questo compito è stato assegnato il 27 Febbraio 1986 a una classe 5ª del Liceo Scientifico.
Argomenti: problema di massimo in geometria piana e solida; massimo per via elementare;
studio di una funzione goniometrica fratta; deduzione del grafico qualitativo del logaritmo
di una funzione a partire dal grafico della funzione stessa; invertibilità di una funzione;
derivata in un punto della funzione inversa; iniettività di una funzione.
Si consideri una circonferenza di diametro \( AB=2R \) e si conduca per il punto \( A \), perpendicolarmente al piano su cui giace la circonferenza, il segmento \( AP=l \).
Se \( CD \) è una corda della circonferenza perpendicolare ad \( AB \), si determini per quale posizione di \( CD \) risulta massimo il volume della piramide \( PACD \).
Si risolva il problema anche per via elementare.
Osserviamo la figura seguente, in cui sono indicati la circonferenza di diametro \( AB=2R \), la corda \( CD \) perpendicolare ad \( AB \), il segmento \( AP=l \) e la piramide \( PACD \):
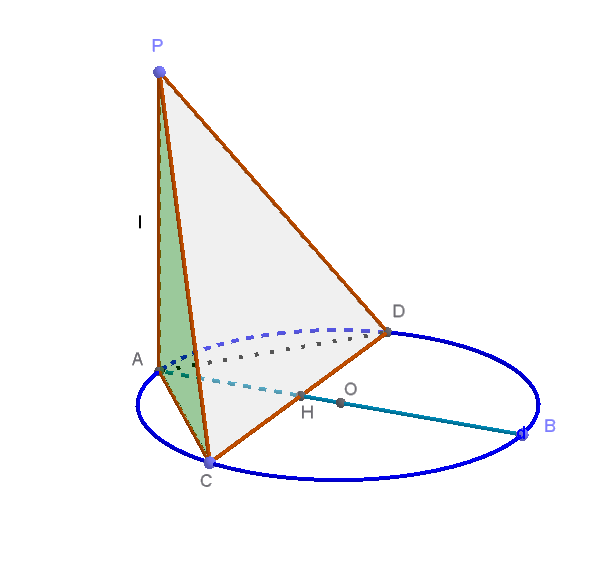
Il volume della piramide, che ha per base il triangolo \( ACD \) e per altezza \( AP \), è dato da:
\[ V_{PACD} = \frac{1}{3} \cdot Area(ACD) \cdot AP = \frac{1}{3} \cdot Area(ACD) \cdot l \]
Essendo \( l \) una costante, il volume è massimo quando è massima l'area di base \( Area(ACD) \). Poniamo \( z = Area(ACD) \).
Consideriamo la circonferenza con inscritto il triangolo \( ACD \), con diametro \( AB \) perpendicolare a \( CD \) e \( H \) piede dell'altezza del triangolo uscente da \( A \):
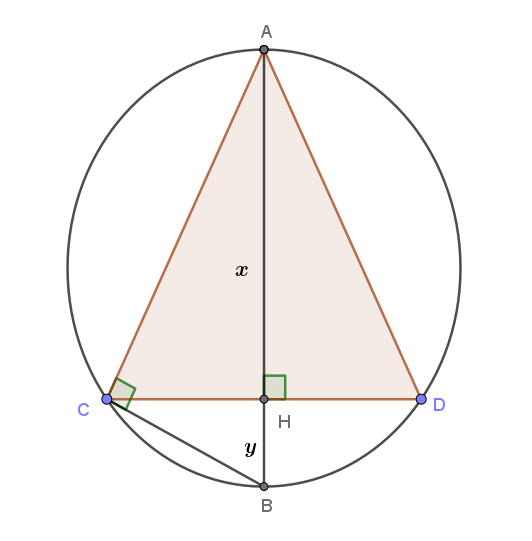
Poniamo:
\( AH = x \), con \( 0 \leq x \leq 2R \)
\( BH = y \), con \( 0 \leq y \leq 2R \)
Risulta:
\[ z = Area(ACD) = \frac{1}{2} \cdot CD \cdot AH = CH \cdot AH \]
Il triangolo \( ACB \) è rettangolo in \( C \) poiché inscritto in una semicirconferenza di diametro \( AB \). Per il Secondo Teorema di Euclide applicato al triangolo \( ACB \), abbiamo: \[ CH = \sqrt{AH \cdot BH} = \sqrt{x \cdot y} \]
Essendo \( y = 2R - x \), l'area \( z \) in funzione di \( x \) è:
\[ z(x) = Area(ACD) = x \cdot CH = x \sqrt{x \cdot y} = x \sqrt{x(2R-x)} \]
Poiché \( z \geq 0 \), l'area è massima quando lo è il suo quadrato \( z^2 = u \). \[ u(x) = z^2 = x^2 (x(2R-x)) = 2Rx^3 - x^4 \] Cerchiamo il massimo assoluto di \( u(x) \) nell'intervallo \( [0, 2R] \).
Calcoliamo la derivata prima \( u'(x) \):
\[ u'(x) = \frac{d}{dx} (2Rx^3 - x^4) = 6Rx^2 - 4x^3 \]
Studiamo il segno di \( u'(x) \):
\[ u'(x) \geq 0 \quad \Rightarrow \quad 2x^2 (3R - 2x) \geq 0 \]
Poiché \( x^2 \geq 0 \), il segno dipende solo da \( 3R - 2x \):
\[ 3R - 2x \geq 0 \quad \Rightarrow \quad 2x \leq 3R \quad \Rightarrow \quad x \leq \frac{3R}{2} \]
Quindi:
\( u(x) \) è **crescente** se \( 0 \leq x < \frac{3R}{2} \)
\( u(x) \) è **decrescente** se \( \frac{3R}{2} < x \leq 2R \)
Pertanto \( u \) (e di conseguenza l'area \( z \) e il volume \( V \)) è massima per \( \mathbf{x = \frac{3R}{2}} \).
Calcolo del Volume Massimo \( V_{max} \):
Per \( x = \frac{3R}{2} \), si ha:
\( AH = x = \frac{3R}{2} \)
\( BH = y = 2R - x = 2R - \frac{3R}{2} = \frac{R}{2} \)
\( CH = \sqrt{x \cdot y} = \sqrt{\frac{3R}{2} \cdot \frac{R}{2}} = \frac{R\sqrt{3}}{2} \)
L'area massima di base è:
\[ Area_{max}(ACD) = CH \cdot AH = \left( \frac{R\sqrt{3}}{2} \right) \cdot \left( \frac{3R}{2} \right) = \frac{3R^2 \sqrt{3}}{4} \]
Il volume massimo è dato da:
\[ V_{max} = \frac{1}{3} \cdot Area_{max}(ACD) \cdot l = \frac{1}{3} \cdot \left( \frac{3R^2 \sqrt{3}}{4} \right) \cdot l = \frac{R^2 l \sqrt{3}}{4} \]
Abbiamo detto che l'area \( z = Area(ACD) = x \sqrt{x \cdot y} \). Riscriviamo l'espressione con esponenti razionali:
\[ z(x,y) = x \cdot x^{1/2} \cdot y^{1/2} = x^{3/2} y^{1/2} \]
Osserviamo che \( x + y = 2R = \text{costante} \).
Ricordiamo la proprietà: Il prodotto di due potenze con la somma delle basi costante è massimo quando le basi sono proporzionali ai rispettivi esponenti.
Nel nostro caso, il massimo si ha quando:
\[ x : \frac{3}{2} = y : \frac{1}{2} \]
Da cui si ottiene:
\[ \frac{1}{2} x = \frac{3}{2} y \quad \Rightarrow \quad x = 3y \]
Sostituendo nella relazione \( x + y = 2R \):
\[ 3y + y = 2R \quad \Rightarrow \quad 4y = 2R \quad \Rightarrow \quad y = \frac{R}{2} \]
E quindi:
\[ x = 3y = 3 \cdot \frac{R}{2} = \frac{3R}{2} \]
Risposta finale: L'area (e quindi il volume) della piramide è massima quando \( AH = \frac{3R}{2} \). Osserviamo che il volume massimo si ha quando il triangolo ACD è equilatero.
Si studi la funzione di equazione
\[ y = f(x) = \frac{4\cos^2(x) - 3}{\cos(x)} \]
nell'intervallo \( [0, 2\pi] \) e se ne disegni il grafico.
Dedurre poi dal grafico di \( y=f(x) \) un grafico qualitativo di \( y=\ln(f(x)) \), indicando i passaggi necessari per dedurre tale grafico.
La funzione da studiare è:
\[ y = f(x) = \frac{4\cos^2(x) - 3}{\cos(x)} \]
L'intervallo di studio è \( [0, 2\pi] \).
La funzione è definita se il denominatore è diverso da zero: \( \cos(x) \neq 0 \). Il dominio \( D \) è:
\[ D = \left[0, \frac{\pi}{2}\right) \cup \left(\frac{\pi}{2}, \frac{3\pi}{2}\right) \cup \left(\frac{3\pi}{2}, 2\pi\right] \]
Asse y (\( x=0 \)): \( f(0) = 1 \). Punto: \((0, 1)\)
Asse x (\( y=0 \)): \( 4\cos^2(x) - 3 = 0 \quad \Rightarrow \quad \cos(x) = \pm \frac{\sqrt{3}}{2} \).
Le intersezioni sono: \( x = \frac{\pi}{6}, \frac{5\pi}{6}, \frac{7\pi}{6}, \frac{11\pi}{6} \).
La funzione è pari poiché \( f(-x) = f(x) \).
Studiamo \( f(x) > 0 \) in base al segno del numeratore \( N \) e del denominatore \( D \):
| Intervallo | \( N \) | \( D \) | \( f(x) \) |
|---|---|---|---|
| \( [0, \frac{\pi}{6}) \) | \( + \) | \( + \) | \( \mathbf{+} \) |
| \( (\frac{\pi}{6}, \frac{\pi}{2}) \) | \( - \) | \( + \) | \( \mathbf{-} \) |
| \( (\frac{\pi}{2}, \frac{5\pi}{6}) \) | \( - \) | \( - \) | \( \mathbf{+} \) |
| \( (\frac{5\pi}{6}, \frac{7\pi}{6}) \) | \( + \) | \( - \) | \( \mathbf{-} \) |
| \( (\frac{7\pi}{6}, \frac{3\pi}{2}) \) | \( - \) | \( - \) | \( \mathbf{+} \) |
| \( (\frac{3\pi}{2}, \frac{11\pi}{6}) \) | \( - \) | \( + \) | \( \mathbf{-} \) |
| \( (\frac{11\pi}{6}, 2\pi] \) | \( + \) | \( + \) | \( \mathbf{+} \) |
In \( x = \frac{\pi}{2} \) e \( x = \frac{3\pi}{2} \) si hanno asintoti verticali:
Asintoto \( x = \frac{\pi}{2} \): \( \lim_{x \to \frac{\pi}{2}^-} f(x) = -\infty \), \( \lim_{x \to \frac{\pi}{2}^+} f(x) = +\infty \)
Asintoto \( x = \frac{3\pi}{2} \): \( \lim_{x \to \frac{3\pi}{2}^-} f(x) = +\infty \), \( \lim_{x \to \frac{3\pi}{2}^+} f(x) = -\infty \)
La derivata prima \( f'(x) \) è stata calcolata come:
\[ f'(x) = \frac{\sin(x) (-4\cos^2(x) - 3)}{\cos^2(x)} = - \frac{\sin(x) (4\cos^2(x) + 3)}{\cos^2(x)} \]
Poiché \( (4\cos^2(x) + 3) \) e \( \cos^2(x) \) sono sempre positivi nel dominio, il segno di \( f'(x) \) è determinato dal fattore \( - \sin(x) \).
Studiamo il segno di \( f'(x) \) tenendo conto degli asintoti verticali in \( x = \frac{\pi}{2} \) e \( x = \frac{3\pi}{2} \):
| Intervallo | \( \sin(x) \) | \( - \sin(x) \) | \( f'(x) \) | Monotonia |
|---|---|---|---|---|
| \( (0, \frac{\pi}{2}) \) | \( + \) | \( - \) | \( - \) | **Decresce** \( \searrow \) |
| \( (\frac{\pi}{2}, \pi) \) | \( + \) | \( - \) | \( - \) | **Decresce** \( \searrow \) |
| \( (\pi, \frac{3\pi}{2}) \) | \( - \) | \( + \) | \( + \) | **Cresce** \( \nearrow \) |
| \( (\frac{3\pi}{2}, 2\pi) \) | \( - \) | \( + \) | \( + \) | **Cresce** \( \nearrow \) |
Massimi e Minimi:
Massimi assoluti: \( x = 0 \) e \( x = 2\pi \) (valore \( y=1 \))
Minimo relativo: \( x = \pi \). La funzione passa da decrescente a crescente, e \( f(\pi) = \frac{4(-1)^2 - 3}{-1} = -1 \). Punto: \( (\pi, -1) \)
La derivata seconda \( f''(x) \) è:
\[ f''(x) = \frac{-4\cos^4(x) + 3\cos^2(x) - 6}{\cos^3(x)} \]
Studiamo il segno del numeratore \( N(x) \):
\[ N(x) = -4\cos^4(x) + 3\cos^2(x) - 6 \]
Poniamo la sostituzione \( t = \cos^2(x) \). Poiché \( x \in D \), si ha \( t \in (0, 1] \). Il numeratore diventa la funzione quadratica in \( t \):
\[ h(t) = -4t^2 + 3t - 6 \]
Calcoliamo il discriminante (\( \Delta \)) del trinomio \( h(t) \):
\[ \Delta = b^2 - 4ac = (3)^2 - 4(-4)(-6) = 9 - 96 = -87 \]
Poiché il discriminante è **negativo** (\( \Delta < 0 \)) e il coefficiente del termine di grado massimo è **negativo** (\( a = -4 < 0 \)), la funzione \( h(t) \) non ha radici reali ed è sempre negativa per ogni \( t \in \mathbb{R} \).
Conclusione: \( N(x) = -4\cos^4(x) + 3\cos^2(x) - 6 < 0 \) per ogni \( x \) nel dominio.
Il segno di \( f''(x) \) dipende quindi unicamente dal segno del denominatore \( \cos^3(x) \), che ha lo stesso segno di \(cos(x)\):
| Intervallo | \( \cos^3(x) \) | \( f''(x) \) | Concavità |
|---|---|---|---|
| \( [0, \frac{\pi}{2}) \) | \( + \) | \( - \) | Verso il basso \( \cap \) |
| \( (\frac{\pi}{2}, \frac{3\pi}{2}) \) | \( - \) | \( + \) | Verso l'alto \( \cup \) |
| \( (\frac{3\pi}{2}, 2\pi] \) | \( + \) | \( - \) | Verso il basso \( \cap \) |
Non ci sono punti di flesso interni al dominio.
Il grafico della funzione è quindi il seguente:
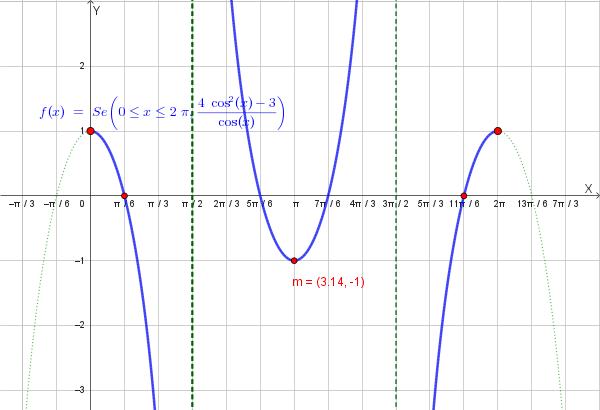
La funzione \( y = \ln(f(x)) \) è definita dove \( f(x) > 0 \). Il dominio \( D' \) è:
\[ D' = \left[0, \frac{\pi}{6}\right) \cup \left(\frac{\pi}{2}, \frac{5\pi}{6}\right) \cup \left(\frac{7\pi}{6}, \frac{3\pi}{2}\right) \cup \left(\frac{11\pi}{6}, 2\pi\right] \]
Intersezioni con l'asse x: \( \ln(f(x)) = 0 \quad \Rightarrow \quad f(x) = 1 \).
Le intersezioni si hanno per \( x = 0, x = 2\pi \) e per i due valori \( \alpha \) e \( \beta \) tali che \( \cos(x) = -\frac{3}{4} \).
Comportamento agli estremi e Monotonia:
Gli zeri di \( f(x) \) e gli asintoti verticali di \( f(x) \) diventano tutti **asintoti verticali** di \( \ln(f(x)) \) (tendenti a \( -\infty \) o a \( +\infty \)).
\( y=\ln(f(x)) \) mantiene la **stessa monotonia** di \( f(x) \) nel suo dominio \( D' \).
Il grafico qualitativo di \( y=\ln(f(x)) \) è quindi il seguente:
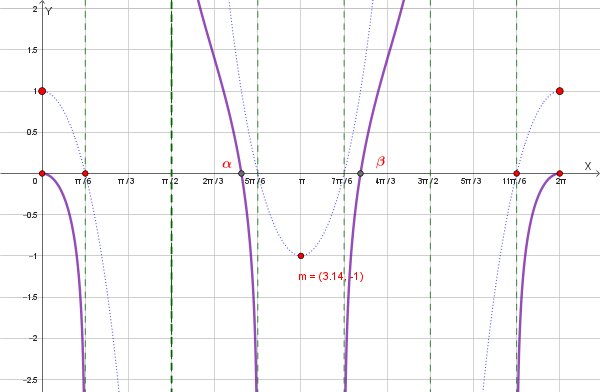
Si consideri la funzione di equazione:
\[ y = f(x) = \frac{e^{2x^2}}{x^2 + 2} \]
a) Dimostrare che la funzione non è invertibile in tutto il suo dominio.
b) Verificare che è invertibile nell'intervallo \( I=(-\infty, 0] \).
c) Detta \( g \) la funzione inversa di \( f \) in \( I \), calcolare \( g'\left(\frac{e^2}{3}\right) \).
La funzione da studiare è:
\[ y = f(x) = \frac{e^{2x^2}}{x^2 + 2} \]
1. Dominio: \( D = (-\infty, +\infty) = \mathbb{R} \).
2. Calcolo della derivata prima \( f'(x) \):
Utilizziamo la regola di derivazione del quoziente: \( \left(\frac{A}{B}\right)' = \frac{A'B - AB'}{B^2} \). Sia \( A = e^{2x^2} \) e \( B = x^2 + 2 \).
Derivata del numeratore: \( A' = \frac{d}{dx}(e^{2x^2}) = e^{2x^2} \cdot \frac{d}{dx}(2x^2) = 4xe^{2x^2} \)
Derivata del denominatore: \( B' = \frac{d}{dx}(x^2 + 2) = 2x \)
Applichiamo la formula del quoziente:
\[ f'(x) = \frac{(4xe^{2x^2}) (x^2 + 2) - (e^{2x^2}) (2x)}{(x^2 + 2)^2} \]
Raccogliamo il termine comune \( 2xe^{2x^2} \) al numeratore:
\[ f'(x) = \frac{2xe^{2x^2} [2(x^2 + 2) - 1]}{(x^2 + 2)^2} \]
Semplifichiamo l'espressione tra parentesi quadre:
\[ 2(x^2 + 2) - 1 = 2x^2 + 4 - 1 = 2x^2 + 3 \]
Quindi, la derivata prima è:
\[ f'(x) = \frac{2xe^{2x^2} (2x^2 + 3)}{(x^2 + 2)^2} \]
3. Studio del segno di \( f'(x) \) e Monotonia:
Notiamo che il segno della derivata prima dipende dal segno d \(x\). Quindi:
\( f'(x) < 0 \) se \( x < 0 \) (funzione **decrescente**)
\( f'(x) > 0 \) se \( x > 0 \) (funzione **crescente**)
4. Deduzione della non invertibilità (Iniettività):
La funzione non è strettamente monotona in tutto \( \mathbb{R} \). Sebbene la **monotonia** sia una condizione **sufficiente** per l'invertibilità, essa **non è necessaria** (vedi nota finale). Pertanto, la sola non-monotonia non basta a concludere la non-invertibilità.
Tuttavia, verifichiamo la simmetria della funzione:
\[ f(-x) = \frac{e^{2(-x)^2}}{(-x)^2 + 2} = \frac{e^{2x^2}}{x^2 + 2} = f(x) \]
Poiché \( f(-x) = f(x) \), la funzione \( f(x) \) è **pari** e il suo grafico è **simmetrico rispetto all'asse delle ordinate** (\(y\)).
Questo implica che, per ogni \( x \neq 0 \), esiste un \( -x \neq x \) tale che \( f(-x) = f(x) \). La funzione **non è iniettiva** e, di conseguenza, **non è invertibile** in tutto il suo dominio \( \mathbb{R} \).
Nell'intervallo \( I=(-\infty, 0] \), la funzione è **strettamente decrescente** (\( f'(x) < 0 \) per \( x < 0 \)). Una funzione strettamente monotona è iniettiva e quindi è **invertibile** nell'intervallo \( I \). Sia \( g \) la funzione inversa di \( f \) in questo intervallo.
Per calcolare la derivata della funzione inversa \( g'(y_0) \), utilizziamo il teorema sulla derivata della funzione inversa:
\[ g'(y_0) = \frac{1}{f'(x_0)} \quad \text{dove } y_0 = f(x_0) \]
Conosciamo \( y_0 = \frac{e^2}{3} \). Troviamo \( x_0 \in I=(-\infty, 0] \) risolvendo \( f(x_0) = \frac{e^2}{3} \). Si trova \( x_0 = -1 \).
Calcolo di \( f'(x_0) = f'(-1) \):
\[ f'(-1) = \frac{2(-1)e^{2} (2(1) + 3)}{(1 + 2)^2} = -\frac{10e^2}{9} \]
Calcolo di \( g'\left(\frac{e^2}{3}\right) \):
\[ g'\left(\frac{e^2}{3}\right) = \frac{1}{f'(-1)} = \frac{1}{-\frac{10e^2}{9}} \] \[ g'\left(\frac{e^2}{3}\right) = -\frac{9}{10e^2} \]
Abbiamo osservato che la **monotonia** è una condizione **sufficiente** per l'invertibilità di una funzione, ma **non necessaria**.
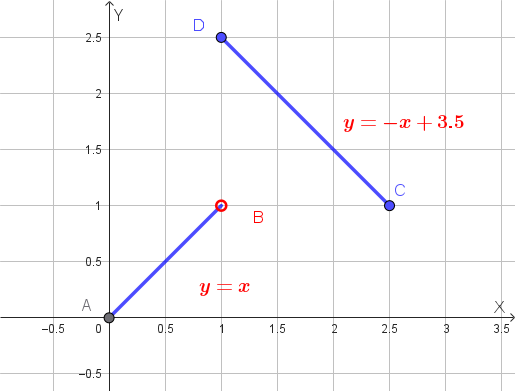
Si consideri, ad esempio, la funzione \( f(x) \) definita a tratti:
\[ f(x)= \begin{cases} x & \text{se } 0 \le x < 1 \\ -x+3.5 & \text{se } 1 \le x \le 2.5 \end{cases} \]
Questa funzione è definita nell'intervallo chiuso \( [0, 2.5] \) e ha come immagine \( [0, 2.5] \). Il suo grafico dimostra chiaramente che la funzione **NON È MONOTONA** su tutto il dominio, eppure è **INIETTIVA** (ogni valore \( y \) è raggiunto una sola volta). Di conseguenza, la funzione **È INVERTIBILE**.
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.