



Questo compito è stato assegnato nel mese di Dicembre 1985 a una classe 5ª del Liceo Scientifico.
Argomenti: Funzione razionale fratta con parametri, studio di funzione razionale fratta,
Studio del moto di un punto, Studio di una funzione goniometrica e legame col moto di un punto, Animazione del moto di un punto su una retta, Studio di una funzione logaritmica,
Curve tangenti.
a) Determinare \(a\), \(b\) e \(c\) in modo che la curva di equazione
\[ y = f(x) = \frac{ax^2 + 4x + b}{cx^2 + 1} \]
ammetta l'asintoto \(y = 2\) ed abbia un massimo nel punto \(M = \left(\frac{1}{2}, 6\right)\).
b) Studiare la funzione ottenuta ponendo \(a = 2\), \(b = 5\) e \(c = 1\) e rappresentarla graficamente in modo qualitativo.
c) Supponendo che un punto materiale si muova su una retta con la legge oraria \(s = f(t)\), con \(t \geq 0\), essendo \(f(x)\) la funzione del punto precedente, si descriva il moto del punto, indicando in particolare la posizione e la velocità iniziali, la massima distanza dall'origine del moto. Si studi poi il moto in termini di velocità e accelerazione (sfruttando lo studio della funzione \(y = f(x)\) del punto b), indicando il significato fisico del punto di flesso che si trova a destra del punto di massimo. Si spieghi infine dove si trova il punto quando il tempo \(t\) tende all'infinito.
Condizione 1: Asintoto orizzontale \(y = 2\)
Per una funzione razionale fratta del tipo \(\frac{ax^2 + 4x + b}{cx^2 + 1}\), l'asintoto orizzontale si trova calcolando:
\[ \lim_{x \to \infty} f(x) = \lim_{x \to \infty} \frac{ax^2 + 4x + b}{cx^2 + 1} = \frac{a}{c} \]
Poiché l'asintoto è \(y = 2\), deve essere:
\[ \frac{a}{c} = 2 \quad \Rightarrow \quad a = 2c \]
Condizione 2: Massimo nel punto \(M = \left(\frac{1}{2}, 6\right)\)
Questa condizione implica due cose:
Dalla prima condizione:
\[ f\left(\frac{1}{2}\right) = \frac{a \cdot \frac{1}{4} + 4 \cdot \frac{1}{2} + b}{c \cdot \frac{1}{4} + 1} = \frac{\frac{a}{4} + 2 + b}{\frac{c}{4} + 1} = 6 \]
Moltiplicando per il denominatore:
\[ \frac{a}{4} + 2 + b = 6\left(\frac{c}{4} + 1\right) = \frac{6c}{4} + 6 \]
\[ \frac{a}{4} + b = \frac{6c}{4} + 4 \]
Moltiplicando per 4:
\[ a + 4b = 6c + 16 \quad \text{...(equazione 1)} \]
Dalla seconda condizione:
Calcoliamo la derivata di \(f(x)\) usando la regola del quoziente:
\[ f'(x) = \frac{(2ax + 4)(cx^2 + 1) - (ax^2 + 4x + b)(2cx)}{(cx^2 + 1)^2} \]
Nel punto \(x = \frac{1}{2}\), il numeratore deve essere zero:
\[ \left(2a \cdot \frac{1}{2} + 4\right)\left(c \cdot \frac{1}{4} + 1\right) - \left(a \cdot \frac{1}{4} + 4 \cdot \frac{1}{2} + b\right)\left(2c \cdot \frac{1}{2}\right) = 0 \]
\[ (a + 4)\left(\frac{c}{4} + 1\right) - \left(\frac{a}{4} + 2 + b\right) \cdot c = 0 \]
Sviluppando:
\[ \frac{ac}{4} + a + c + 4 - \frac{ac}{4} - 2c - bc = 0 \]
\[ a - c + 4 - bc = 0 \]
\[ a = c + bc - 4 \quad \text{...(equazione 2)} \]
Sistema di equazioni:
Abbiamo tre equazioni con tre incognite:
Dalla (1) e (3):
\[ 2c = c + bc - 4 \quad \Rightarrow \quad c = bc - 4 \quad \Rightarrow \quad c(1 - b) = -4 \quad \Rightarrow \quad c = \frac{4}{b - 1} \]
Sostituendo \(a = 2c\) nell'equazione (2):
\[ 2c + 4b = 6c + 16 \quad \Rightarrow \quad 4b = 4c + 16 \quad \Rightarrow \quad b = c + 4 \]
Sostituendo \(c = \frac{4}{b-1}\) in \(b = c + 4\):
\[ b = \frac{4}{b-1} + 4 \quad \Rightarrow \quad b(b-1) = 4 + 4(b-1) \quad \Rightarrow \quad b^2 - b = 4b \]
\[ b^2 - 5b = 0 \quad \Rightarrow \quad b(b-5) = 0 \]
Le soluzioni sono \(b = 0\) o \(b = 5\).
Se \(b = 0\): \(c = \frac{4}{-1} = -4\) e \(a = 2c = -8\)
Se \(b = 5\): \(c = \frac{4}{4} = 1\) e \(a = 2c = 2\)
Verifica: Dobbiamo verificare quale soluzione corrisponde a un massimo. Con \(a = 2\), \(b = 5\), \(c = 1\) otteniamo la funzione che studieremo al punto b).
Risposta: \(a = 2\), \(b = 5\), \(c = 1\) (oppure \(a = -8\), \(b = 0\), \(c = -4\))
La funzione da studiare è:
\[ y = f(x) = \frac{2x^2 + 4x + 5}{x^2 + 1} \]
1. Dominio
Il denominatore \(x^2 + 1\) è sempre positivo per ogni \(x \in \mathbb{R}\), quindi:
\[ D = \mathbb{R} \]
2. Intersezioni con gli assi
3. Segno della funzione
Poiché il numeratore non ha radici reali e ha coefficiente positivo, è sempre positivo. Il denominatore è sempre positivo. Quindi:
\[ f(x) > 0 \quad \forall x \in \mathbb{R} \]
4. Limiti e asintoti
Asintoti orizzontali:
\[ \lim_{x \to \pm\infty} f(x) = \lim_{x \to \pm\infty} \frac{2x^2 + 4x + 5}{x^2 + 1} = 2 \]
Asintoto orizzontale: \(y = 2\)
Asintoti verticali: Non esistono (dominio = \(\mathbb{R}\))
5. Derivata prima (monotonia)
\[ f'(x) = \frac{(4x + 4)(x^2 + 1) - (2x^2 + 4x + 5)(2x)}{(x^2 + 1)^2} \]
\[ = \frac{4x^3 + 4x + 4x^2 + 4 - 4x^3 - 8x^2 - 10x}{(x^2 + 1)^2} = \frac{-4x^2 - 6x + 4}{(x^2 + 1)^2} \]
\[ = \frac{-2(2x^2 + 3x - 2)}{(x^2 + 1)^2} \]
Punti critici: \(2x^2 + 3x - 2 = 0\)
\[ x = \frac{-3 \pm \sqrt{9 + 16}}{4} = \frac{-3 \pm \sqrt{25}}{4} = \frac{-3 \pm 5}{4} \]
Quindi: \(x_1 = \frac{-3 - 5}{4} = -2\) e \(x_2 = \frac{-3 + 5}{4} = \frac{1}{2}\)
Studio del segno di \(f'(x)\):
Il segno di \(f'(x)\) è determinato dal segno di \(-2(2x^2 + 3x - 2)\), cioè dall'opposto di \(2x^2 + 3x - 2\).
Il trinomio \(2x^2 + 3x - 2\) ha il primo coefficiente positivo e zeri in \(x = -2\) e \(x = \frac{1}{2}\).
Massimi e minimi:
6. Derivata seconda (concavità)
Per studiare la concavità della funzione, calcoliamo la derivata seconda.
Partendo da:
\[ f'(x) = \frac{-4x^2 - 6x + 4}{(x^2 + 1)^2} \]
Applichiamo la regola del quoziente:
\[ f''(x) = \frac{(-8x - 6)(x^2 + 1)^2 - (-4x^2 - 6x + 4) \cdot 2(x^2 + 1) \cdot 2x}{(x^2 + 1)^4} \]
Semplifichiamo raccogliendo \((x^2 + 1)\) al numeratore:
\[ f''(x) = \frac{(x^2 + 1)[(-8x - 6)(x^2 + 1) - 4x(-4x^2 - 6x + 4)]}{(x^2 + 1)^4} \]
\[ = \frac{(-8x - 6)(x^2 + 1) - 4x(-4x^2 - 6x + 4)}{(x^2 + 1)^3} \]
Sviluppiamo il numeratore:
\[ (-8x - 6)(x^2 + 1) = -8x^3 - 8x - 6x^2 - 6 = -8x^3 - 6x^2 - 8x - 6 \]
\[ -4x(-4x^2 - 6x + 4) = 16x^3 + 24x^2 - 16x \]
Sommando:
\[ -8x^3 - 6x^2 - 8x - 6 + 16x^3 + 24x^2 - 16x \]
\[ = 8x^3 + 18x^2 - 24x - 6 \]
Quindi:
\[ f''(x) = \frac{8x^3 + 18x^2 - 24x - 6}{(x^2 + 1)^3} = \frac{2(4x^3 + 9x^2 - 12x - 3)}{(x^2 + 1)^3} \]
Studio del segno di \(f''(x)\):
Il segno di \(f''(x)\) dipende dal segno del numeratore \(4x^3 + 9x^2 - 12x - 3\), poiché il denominatore è sempre positivo.
Cerchiamo gli zeri del polinomio \(4x^3 + 9x^2 - 12x - 3 = 0\).
Proviamo con valori semplici. Per \(x = -3\):
\[ 4(-27) + 9(9) - 12(-3) - 3 = -108 + 81 + 36 - 3 = 6 \neq 0 \]
Per \(x = 1\):
\[ 4(1) + 9(1) - 12(1) - 3 = 4 + 9 - 12 - 3 = -2 \neq 0 \]
Per \(x = -\frac{1}{2}\):
\[ 4\left(-\frac{1}{8}\right) + 9\left(\frac{1}{4}\right) - 12\left(-\frac{1}{2}\right) - 3 = -\frac{1}{2} + \frac{9}{4} + 6 - 3 = -\frac{2}{4} + \frac{9}{4} + 3 = \frac{7}{4} + 3 \neq 0 \]
Non ci sono radici razionali semplici. Dallo studio della derivata prima e dall'esistenza dell'asintoto orizzontale \(y = 2\) possiamo dedurre che ci sono tre flessi di ascisse:
\[ x_{F_1} < -2, \quad x_{F_2} \text{ compreso fra } -2 \text{ e } \frac{1}{2}, \quad x_{F_3} > \frac{1}{2} \]
N.B. Siccome la derivata seconda in \(x = -2\) è positiva, \(\frac{2}{5}\), e in \(x = 0\) è negativa, \(-6\), il punto di flesso \(x_{F_2}\) si trova fra il minimo e l'origine, cioè nell'intervallo \((-2, 0)\).
Studio della concavità:
Il polinomio cubico \(4x^3 + 9x^2 - 12x - 3\) ha coefficiente direttore positivo (\(a = 4 > 0\)), quindi:
Punti di flesso:
La funzione ha tre punti di flesso nelle ascisse \(x_{F_1}\), \(x_{F_2}\) e \(x_{F_3}\), dove la concavità cambia segno.
In particolare, il flesso \(F_3 \), che che si trova a destra del massimo,ha un significato importante per l'interpretazione fisica nel punto c).
7. Grafico qualitativo
Il grafico mostra una funzione sempre positiva, con asintoto orizzontale \(y = 2\), un minimo locale a sinistra dell'origine e un massimo locale nel punto \(M(1/2, 6)\).
Il grafico è del tipo seguente:
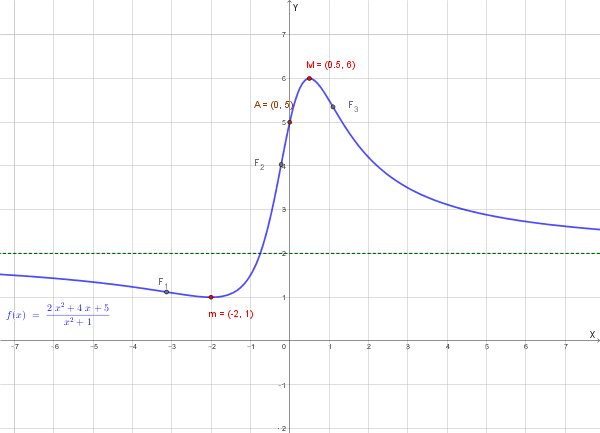
Consideriamo la legge oraria \(s = f(t) = \frac{2t^2 + 4t + 5}{t^2 + 1}\) con \(t > 0\).
Posizione iniziale (\(t = 0\)):
\[ s(0) = f(0) = 5 \text{ (unità di lunghezza)} \]
Velocità:
La velocità è la derivata della posizione rispetto al tempo:
\[ v(t) = f'(t) = \frac{-2(4t^2 + t - 2)}{(t^2 + 1)^2} \]
Velocità iniziale (\(t = 0\)):
\[ v(0) = \frac{-2(0 + 0 - 2)}{1} = \frac{4}{1} = 4 \text{ (unità di velocità)} \]
Massima distanza dall'origine:
Dal punto b), sappiamo che la funzione ha un massimo assoluto in \(t = \frac{1}{2}\) con valore \(f\left(\frac{1}{2}\right) = 6\).
La massima distanza dall'origine è quindi:
\[ s_{max} = 6 \text{ unità, raggiunta all'istante } t = \frac{1}{2} \]
Studio della velocità:
Dallo studio della derivata prima, sappiamo che:
Il punto raggiunge la massima distanza dall'origine quando la velocità si annulla, poi inverte il senso del moto.
Accelerazione:
L'accelerazione è la derivata della velocità:
\[ a(t) = v'(t) = f''(t) \]
Il punto di flesso della funzione \(s = f(t)\) corrisponde al punto in cui l'accelerazione cambia segno, cioè dove la concavità del grafico cambia.
Significato fisico del punto di flesso \(F_3\):
Nel punto di flesso, l'accelerazione è nulla (\(a = 0\)) e cambia segno. In particolare in \(F_3\) il punto materiale passa da un moto con accelerazione negativa ad uno con accelerazione positiva. Questo vuol dire che nel punto di flesso la velocità che stava diminuendo raggiunge il suo valore minimo (negativo) e poi comincia ad aumentare mentre si avvicina al punto che dista 2 dall'origine, tendendo a fermarsi (velocità che tende a zero).
Comportamento per \(t \to +\infty\):
\[ \lim_{t \to +\infty} s(t) = 2 \]
Quando il tempo tende all'infinito, il punto si avvicina asintoticamente alla posizione \(s = 2\) unità dall'origine.
Riepilogo del moto:
• Il punto parte dalla posizione \(s_0 = 5\) con velocità \(v_0 = 4\)
• Si allontana dall'origine fino a raggiungere la massima distanza \(s_{max} = 6\).
• Poi inverte il moto e torna verso l'origine
• Per tempi molto grandi, il punto si avvicina alla posizione \(s = 2\) senza mai raggiungerla.
Si consideri la funzione:
\[ y = f(x) = x \cos(x) \]
a) Si tracci un grafico qualitativo della funzione nell'intervallo \([-\pi, \pi]\), indicando i valori approssimati a meno di un decimo dei punti di massimo e minimo relativi interni all'intervallo. Non è richiesto lo studio della derivata seconda.
b) Considerando la funzione \(s = f(t)\) (con \(t\) in secondi ed \(s\) in metri), descrivi il moto di un punto P che si muove su una retta secondo la legge oraria \(s = f(t)\), con \(t \geq 0\). Si calcoli (approssimando al decimo di secondo) il primo istante dopo la partenza in cui la velocità del punto si annulla e spiega cosa succede dopo questo istante fino all'istante \(t = 3{,}14\) secondi.
Dominio:
La funzione \(f(x) = x \cos(x)\) è il prodotto di due funzioni elementari continue su tutto \(\mathbb{R}\). Quindi:
\[ D = \mathbb{R} \]
Tuttavia, ai fini del problema, considereremo la funzione nell'intervallo \([-\pi, \pi]\).
Intersezioni con gli assi:
Parità/Disparità:
Verifichiamo se la funzione è pari o dispari calcolando \(f(-x)\):
\[ f(-x) = (-x) \cos(-x) = -x \cos(x) = -f(x) \]
Poiché \(f(-x) = -f(x)\), la funzione è dispari. Il grafico è quindi simmetrico rispetto all'origine.
Segno della funzione:
Il segno di \(f(x) = x \cos(x)\) dipende dal segno del prodotto tra \(x\) e \(\cos(x)\).
Analizziamo il segno nell'intervallo \([0, \pi]\) (per simmetria, il segno in \([-\pi, 0]\) sarà opposto):
Valori agli estremi dell'intervallo:
Poiché la funzione è continua nell'intervallo chiuso e limitato \([-\pi, \pi]\), non è necessario calcolare limiti. Calcoliamo direttamente i valori:
\[ f(-\pi) = -\pi \cos(-\pi) = -\pi \cdot (-1) = \pi \approx 3{,}14 \]
\[ f(\pi) = \pi \cos(\pi) = \pi \cdot (-1) = -\pi \approx -3{,}14 \]
Derivata prima e monotonia:
Calcoliamo la derivata prima applicando la regola del prodotto:
\[ f'(x) = \cos(x) + x \cdot (-\sin(x)) = \cos(x) - x \sin(x) \]
I punti critici si trovano risolvendo \(f'(x) = 0\):
\[ \cos(x) - x \sin(x) = 0 \quad \Rightarrow \quad \cos(x) = x \sin(x) \]
Verifichiamo il caso \(x = 0\): sostituendo nella condizione \(f'(x) = 0\):
\[ f'(0) = \cos(0) - 0 \cdot \sin(0) = 1 - 0 = 1 \neq 0 \]
Quindi \(x = 0\) non è un punto critico.
Per \(x \neq 0\), quando \(\cos(x) \neq 0\) possiamo dividere per \(\cos(x)\):
\[ 1 = x \frac{\sin(x)}{\cos(x)} \quad \Rightarrow \quad \tan(x) = \frac{1}{x} \]
Verifichiamo il caso \(\cos(x) = 0\): nell'intervallo \([-\pi, \pi]\), ciò accade per \(x = \pm\frac{\pi}{2}\). Sostituendo nella condizione \(f'(x) = 0\):
\[ \cos\left(\pm\frac{\pi}{2}\right) - \left(\pm\frac{\pi}{2}\right) \sin\left(\pm\frac{\pi}{2}\right) = 0 - \left(\pm\frac{\pi}{2}\right) \cdot (\pm 1) = -\frac{\pi}{2} \neq 0 \]
Quindi \(x = \pm\frac{\pi}{2}\) non sono punti critici. I punti critici si trovano risolvendo l'equazione \(\tan(x) = \frac{1}{x}\) per \(x \neq 0\) e \(\cos(x) \neq 0\).
Metodo grafico per trovare i punti critici:
Per trovare le soluzioni dell'equazione \(\tan(x) = \frac{1}{x}\), confrontiamo graficamente le due funzioni \(y = \tan(x)\) e \(y = \frac{1}{x}\).
Confronto grafico fra \(\tan(x)\) e \(\frac{1}{x}\):
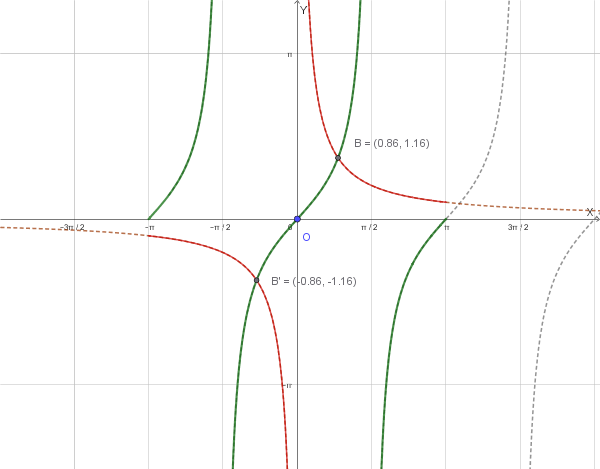
Nell'intervallo \((0, \frac{\pi}{2})\), la curva \(y = \tan(x)\) parte da 0, cresce fino a \(+\infty\) in \(x = \frac{\pi}{2}^-\), mentre \(y = \frac{1}{x}\) è una funzione decrescente che parte da \(+\infty\) e tende a 0. Le due curve si intersecano in un punto compreso tra 0 e \(\frac{\pi}{2}\).
Approssimazione del punto di massimo relativo (positivo):
Effettuiamo una tabulazione per trovare il valore approssimato del punto critico positivo nell'intervallo \((0, \pi)\):
| \(x\) | \(\tan(x)\) | \(\frac{1}{x}\) |
|---|---|---|
| 0,8 | 1,03 | 1,25 |
| 0,9 | 1,26 | 1,11 |
| 0,86 | 1,16 | 1,16 |
Dall'analisi della tabella, osserviamo che l'intersezione avviene approssimativamente per \(x \approx 0{,}9\) (più precisamente \(x \approx 0{,}86\)).
Verifichiamo il valore di \(f(0{,}9)\):
\[ f(0{,}9) = 0{,}9 \cdot \cos(0{,}9) \approx 0{,}9 \cdot 0{,}622 \approx 0{,}56 \]
Quindi, il punto di massimo relativo è approssimativamente \((0{,}9; 0{,}6)\).
Punto di minimo relativo (per simmetria):
Poiché la funzione è dispari, il simmetrico rispetto all'origine del punto di massimo è un punto di minimo relativo:
\[ f(-0{,}9) = -f(0{,}9) \approx -0{,}6 \]
Quindi, il punto di minimo relativo è approssimativamente \((-0{,}9; -0{,}6)\).
Grafico qualitativo:
Utilizzando lo studio fatto, possiamo ora tracciare il grafico qualitativo della funzione. Il grafico è simmetrico rispetto all'origine (funzione dispari), presenta zeri in corrispondenza di \(x = -\frac{\pi}{2}\), \(x = 0\) e \(x = \frac{\pi}{2}\), un massimo relativo in \((0{,}9; 0{,}6)\) e un minimo relativo in \((-0{,}9; -0{,}6)\).
Il grafico qualitativo della funzione è quindi il seguente:
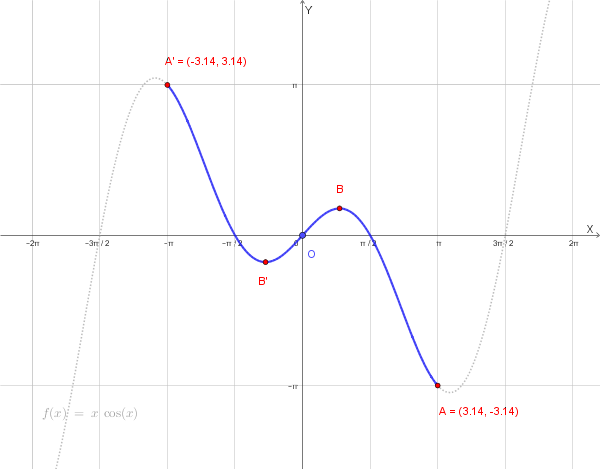
Consideriamo la legge oraria \(s = f(t) = t \cos(t)\) con \(t \geq 0\), dove \(s\) è misurato in metri e \(t\) in secondi.
Posizione iniziale (\(t = 0\)):
\[ s(0) = 0 \cdot \cos(0) = 0 \text{ metri} \]
Il punto parte dall'origine.
Velocità:
La velocità è la derivata della posizione rispetto al tempo:
\[ v(t) = s'(t) = f'(t) = \cos(t) - t \sin(t) \]
Velocità iniziale (\(t = 0\)):
\[ v(0) = \cos(0) - 0 \cdot \sin(0) = 1 - 0 = 1 \text{ m/s} \]
Il punto parte con velocità positiva di 1 m/s, muovendosi nella direzione positiva.
Primo istante in cui la velocità si annulla:
Dal punto a), sappiamo che la velocità si annulla quando \(\tan(t) = \frac{1}{t}\). Dall'approssimazione effettuata, il primo istante in cui ciò accade è:
\[ t \approx 0{,}9 \text{ secondi} \]
In questo istante, la posizione del punto è:
\[ s(0{,}9) = 0{,}9 \cdot \cos(0{,}9) \approx 0{,}6 \text{ metri} \]
Il punto raggiunge la sua massima distanza dall'origine (circa 0,6 metri nella direzione positiva) e la velocità diventa nulla istantaneamente.
Cosa succede dopo \(t = 0{,}9\) secondi fino a \(t = 3{,}14\) secondi:
1. Intervallo \(0{,}9 < t < \frac{\pi}{2}\) (cioè circa \(0{,}9 < t < 1{,}57\) secondi):
2. Istante \(t = \frac{\pi}{2} \approx 1{,}57\) secondi:
\[ s\left(\frac{\pi}{2}\right) = \frac{\pi}{2} \cdot \cos\left(\frac{\pi}{2}\right) = \frac{\pi}{2} \cdot 0 = 0 \text{ metri} \]
Il punto ritorna all'origine attraversandola con velocità negativa.
3. Intervallo \(\frac{\pi}{2} < t \leq \pi\) (cioè circa \(1{,}57 < t \leq 3{,}14\) secondi):
4. Istante finale \(t = \pi \approx 3{,}14\) secondi:
\[ s(\pi) = \pi \cdot \cos(\pi) = \pi \cdot (-1) = -\pi \approx -3{,}14 \text{ metri} \]
Il punto si trova a circa 3,14 metri dall'origine nella direzione negativa.
Riepilogo del moto (0 ≤ t ≤ π secondi):
• t = 0 s: Partenza dall'origine con velocità v = 1 m/s (verso destra)
• t ≈ 0,9 s: Massima distanza dall'origine (s ≈ 0,6 m), velocità si annulla
• 0,9 s < t < 1,57 s: Ritorno verso l'origine con velocità negativa
• t ≈ 1,57 s: Attraversamento dell'origine
• 1,57 s < t ≤ 3,14 s: Movimento nella direzione negativa
• t = 3,14 s: Posizione finale s = -π ≈ -3,14 m
a) Si rappresenti qualitativamente la funzione di equazione \( f(x)=\frac{\ln(x)}{x} \), studiando il dominio, le intersezioni con gli assi, il segno della funzione, i limiti e lo studio della derivata prima.
b) Tra le curve di equazione \( g(x)=\frac{h}{x^2} \) si trovi, se esiste, quella tangente al grafico di \( f(x) \).
a) Studio e grafico della funzione \( f(x)=\frac{\ln(x)}{x} \)
Dominio (Campo di Esistenza)
La funzione è definita se e solo se l'argomento del logaritmo è strettamente positivo (\(\ln(x)\) richiede \( x > 0 \)) e il denominatore è diverso da zero (\( x \neq 0 \)).
Dominio: \( D = (0, +\infty) \)
Intersezioni con gli Assi
Segno della Funzione
Il segno dipende solo dal numeratore \(\ln(x)\), poiché il denominatore \(x\) è sempre positivo nel dominio \( (0, +\infty) \).
Limiti (Comportamento agli Estremi del Dominio)
Limite per \( x \to 0^+ \) (asintoto verticale):
\[ \lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} \frac{\ln(x)}{x} = \frac{-\infty}{0^+} = -\infty \]
La funzione presenta un **asintoto verticale** in \( x=0 \) (l'asse \(y\)).
Limite per \( x \to +\infty \) (asintoto orizzontale):
\[ \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \frac{\ln(x)}{x} \]
Poiché il logaritmo \(\ln(x)\) è un **infinito di ordine inferiore** rispetto al monomio \(x\), il limite del loro rapporto tende a zero.
\[ \lim_{x \to +\infty} \frac{\ln(x)}{x} = 0^+ \]
La funzione presenta un **asintoto orizzontale** in \( y=0 \) (l'asse \(x\)).
Studio della Derivata Prima
Calcoliamo la derivata prima \( f'(x) \) (regola di derivazione di un quoziente):
\[ f'(x) = \frac{(\frac{1}{x}) \cdot x - \ln(x) \cdot 1}{x^2} = \frac{1 - \ln(x)}{x^2} \]
Per trovare i massimi/minimi, poniamo \( f'(x) = 0 \):
\[ 1 - \ln(x) = 0 \implies \ln(x) = 1 \implies x = e \]
Per studiare il segno, notiamo che \( x^2 > 0 \) nel dominio. Quindi il segno dipende solo da \( 1 - \ln(x) \).
Quindi, in \( x=e \) c'è un **punto di massimo relativo**.
L'ordinata del massimo è: \( f(e) = \frac{\ln(e)}{e} = \frac{1}{e} \).
Punto di Massimo: \( M\left(e, \frac{1}{e}\right) \approx (2.71, 0.368) \)
Grafico Qualitativo:
Combinando i risultati (asintoto verticale \( x=0 \), asintoto orizzontale \( y=0 \), intersezione \( (1, 0) \), massimo in \( \left(e, \frac{1}{e}\right) \)), il grafico qualitativo è il seguente:
Questo è il grafico qualitativo:
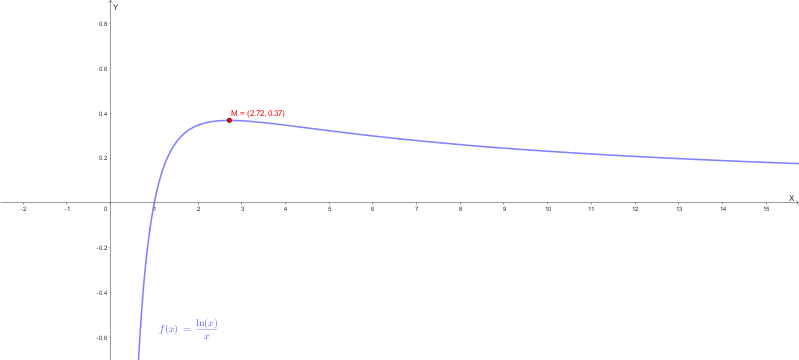
b) Ricerca della curva \( g(x)=\frac{h}{x^2} \) tangente a \( f(x) \)
Affinché le due curve \( f(x) \) e \( g(x) \) siano tangenti, deve esistere un punto \( x_0 \) in cui si verificano due condizioni:
Calcoliamo la derivata di \( g(x) = hx^{-2} \):
\[ g'(x) = h \cdot (-2x^{-3}) = -\frac{2h}{x^3} \]
Le condizioni diventano:
\[ \begin{cases} \frac{\ln(x_0)}{x_0} = \frac{h}{x_0^2} & \text{(1)} \\ \frac{1 - \ln(x_0)}{x_0^2} = -\frac{2h}{x_0^3} & \text{(2)} \end{cases} \]
Dalla (1), moltiplicando per \( x_0^2 \) (ricordando che \( x_0 \neq 0 \)):
\[ h = x_0 \ln(x_0) \]
Sostituiamo questa espressione di \( h \) nella (2) e moltiplichiamo per \( x_0^3 \):
\[ \frac{1 - \ln(x_0)}{x_0^2} = -\frac{2(x_0 \ln(x_0))}{x_0^3} \implies x_0(1 - \ln(x_0)) = -2x_0 \ln(x_0) \]
Dividiamo per \( x_0 \) (poiché \( x_0 \neq 0 \)):
\[ 1 - \ln(x_0) = -2 \ln(x_0) \] \[ 1 = -2 \ln(x_0) + \ln(x_0) \] \[ 1 = -\ln(x_0) \] \[ \ln(x_0) = -1 \] \[ x_0 = e^{-1} = \frac{1}{e} \]
Il punto di tangenza è \( x_0 = \frac{1}{e} \).
Ora, troviamo il valore di \( h \) corrispondente:
\[ h = x_0 \ln(x_0) = \frac{1}{e} \cdot \ln\left(\frac{1}{e}\right) = \frac{1}{e} \cdot (-1) = -\frac{1}{e} \]
Quindi, la curva tangente è quella per cui \( h = -\frac{1}{e} \).
L'equazione della curva tangente è: \( g(x) = \frac{-1/e}{x^2} = -\frac{1}{ex^2} \).
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.