



Questo compito è stato assegnato il 27 Febbraio 1987 a una classe 5ª del Liceo Scientifico.
Argomenti: continuità e derivabilità; punto angoloso; angolo fra due rette; grafico di una funzione definita a tratti;
studio di una funzione logaritmica, Teorema di Rolle, studio di una funzione goniometrica, derivata con la definizione.
Data la funzione:
\[ f(x) = \begin{cases} x^2 + 1 & \text{se } x < 0 \\ e^x & \text{se } x \geq 0 \end{cases} \]
a) Dimostra che è continua su tutto \( \mathbb{R} \).
b) Dimostra che non è derivabile in \( x=0 \) e trova le equazioni della semitangente sinistra e della semitangente destra in \( x=0 \).
c) Calcola l'angolo in gradi sessagesimali fra le due semitangenti, approssimando al decimo.
d) Rappresenta graficamente la funzione e le due semitangenti.
La funzione da analizzare è:
\[ f(x) = \begin{cases} x^2 + 1 & \text{se } x < 0 \\ e^x & \text{se } x \geq 0 \end{cases} \]
La funzione \( f(x) \) è continua per ogni \( x \neq 0 \) perché è definita da funzioni elementari continue nei rispettivi domini: la funzione polinomiale \( x^2 + 1 \) è continua per \( x < 0 \) e la funzione esponenziale \( e^x \) è continua per \( x > 0 \). Quindi, per dimostrare che \( f(x) \) è continua su tutto \( \mathbb{R} \), è sufficiente verificare la continuità nel punto di raccordo \( x = 0 \).
Calcolo dei limiti:
Limite sinistro: \( \displaystyle \lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} (x^2 + 1) = 0^2 + 1 = 1 \)
Limite destro: \( \displaystyle \lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} e^x = e^0 = 1 \)
Valore della funzione: \( f(0) = e^0 = 1 \)
Poiché:
\[ \lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0) = 1 \]
Conclusione: La funzione \( f(x) \) è continua in \( x = 0 \) e quindi su tutto \( \mathbb{R} \).
Calcolo delle derivate:
Per \( x < 0 \): \( f'(x) = 2x \)
Per \( x > 0 \): \( f'(x) = e^x \)
Derivata sinistra in \( x = 0 \):
\[ f'_-(0) = \lim_{x \to 0^-} f'(x) = \lim_{x \to 0^-} 2x = 0 \]
Derivata destra in \( x = 0 \):
\[ f'_+(0) = \lim_{x \to 0^+} f'(x) = \lim_{x \to 0^+} e^x = 1 \]
Poiché \( f'_-(0) = 0 \neq 1 = f'_+(0) \), la funzione non è derivabile in \( x = 0 \).
Equazioni delle semitangenti:
Le semitangenti passano per il punto \( P(0, 1) \).
Semitangente sinistra: coefficiente angolare \( m_s = 0 \)
\[ y = 1 \]
Semitangente destra: coefficiente angolare \( m_d = 1 \)
\[ y - 1 = 1 \cdot (x - 0) \quad \Rightarrow \quad y = x + 1 \]
L'angolo \( \alpha \) tra le due semitangenti si può calcolare considerando che esse formano un angolo con l'asse delle \( x \) rispettivamente di:
Semitangente sinistra: \( \alpha_s = \arctan(0) = 0° \)
Semitangente destra: \( \alpha_d = \arctan(1) = 45° \)
L'angolo acuto tra le due rette sarebbe \( 45° - 0° = 45° \), ma poiché le semitangenti si incontrano nel punto \( (0, 1) \) con orientazioni opposte (una va verso sinistra e l'altra verso destra), l'angolo effettivo tra esse è:
\[ \alpha = 180° - 45° = 135° \]
In alternativa, possiamo osservare geometricamente che la semitangente sinistra è orizzontale e la semitangente destra sale con pendenza 1 (formando 45° con l'orizzontale). L'angolo ottuso compreso tra le due semitangenti è quindi:
\[ \alpha = 180° - 45° = 135° \]
Risposta: L'angolo tra le due semitangenti è \( \mathbf{135{,}0°} \).
Il grafico mostra:
La parabola \( y = x^2 + 1 \) per \( x < 0 \) (in blu)
L'esponenziale \( y = e^x \) per \( x \geq 0 \) (in blu)
Il punto di giunzione \( P(0, 1) \) (in rosso)
La semitangente sinistra \( y = 1 \) (in verde tratteggiato)
La semitangente destra \( y = x + 1 \) (in arancione tratteggiato)
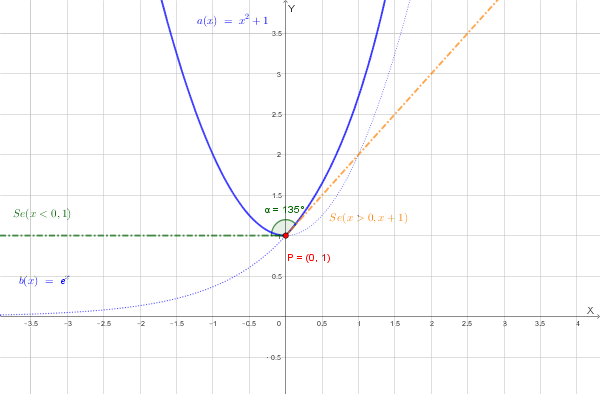
Dal grafico si osserva chiaramente il "punto angoloso" in \( x = 0 \), dove la funzione è continua ma non derivabile, con le due semitangenti che formano un angolo di 135°.
Considera la funzione seguente:
\[ f(x) = \begin{cases} \ln(1 - |1 - x^2|) & \text{se } -\sqrt{2} < x < \sqrt{2} \text{ e } x \neq 0 \\ 0 & \text{se } x = 0 \end{cases} \]
a) Studia la funzione e rappresentala graficamente.
b) Scrivi l'equazione della tangente al grafico di \( f \) nel punto di ascissa \( x = -\frac{1}{2} \).
c) Nell'intervallo \( [-1, 1] \) è applicabile il Teorema di Rolle?
La funzione da studiare è:
\[ f(x) = \begin{cases} \ln(1 - |1 - x^2|) & \text{se } -\sqrt{2} < x < \sqrt{2} \text{ e } x \neq 0 \\ 0 & \text{se } x = 0 \end{cases} \]
Il dominio è dato dall'intervallo \( (-\sqrt{2}, \sqrt{2}) \) con la condizione che l'argomento del logaritmo sia positivo.
Dobbiamo avere: \( 1 - |1 - x^2| > 0 \quad \Rightarrow \quad |1 - x^2| < 1 \)
Dalla definizione di valore assoluto:
\[ -1 < 1 - x^2 < 1 \]
Risolviamo le due disequazioni:
\( 1 - x^2 > -1 \quad \Rightarrow \quad -x^2 > -2 \quad \Rightarrow \quad x^2 < 2 \quad \Rightarrow \quad -\sqrt{2} < x < \sqrt{2} \)
\( 1 - x^2 < 1 \quad \Rightarrow \quad -x^2 < 0 \quad \Rightarrow \quad x^2 > 0 \quad \Rightarrow \quad x \neq 0 \)
Intersecando le due condizioni e considerando che per definizione la funzione vale 0 in \( x = 0 \), il dominio è:
\[ D = (-\sqrt{2}, \sqrt{2}) \]
Verifichiamo se la funzione è pari: \( f(-x) = \ln(1 - |1 - (-x)^2|) = \ln(1 - |1 - x^2|) = f(x) \)
La funzione è pari, quindi simmetrica rispetto all'asse \( y \).
Asse y (\( x=0 \)): \( f(0) = 0 \). Punto: \( (0, 0) \)
Asse x (\( y=0 \)): \( \ln(1 - |1 - x^2|) = 0 \)
\( 1 - |1 - x^2| = 1 \quad \Rightarrow \quad |1 - x^2| = 0 \quad \Rightarrow \quad x^2 = 1 \quad \Rightarrow \quad x = \pm 1 \)
Gli zeri della funzione sono \( x = \pm 1 \); inoltre \( f(0) = 0 \) per definizione.
Studiamo \( f(x) > 0 \):
\( \ln(1 - |1 - x^2|) > 0 \quad \Rightarrow \quad 1 - |1 - x^2| > 1 \quad \Rightarrow \quad |1 - x^2| < 0 \)
Poiché il valore assoluto è sempre non negativo, questa condizione non è mai soddisfatta.
La funzione è sempre negativa o nulla: \( f(x) \leq 0 \) per ogni \( x \in D \).
Limite per \( x \to 0 \):
Per \( x \to 0 \): \( x^2 \to 0 \), quindi \( 1 - x^2 \to 1 \) e \( |1 - x^2| \to 1 \)
\( \displaystyle \lim_{x \to 0} f(x) = \lim_{x \to 0} \ln(1 - |1 - x^2|) = \ln(1 - 1) = \ln(0^+) = -\infty \)
Limite per \( x \to \pm\sqrt{2} \):
Per \( x \to \pm\sqrt{2} \): \( x^2 \to 2 \), quindi \( 1 - x^2 \to -1 \) e \( |1 - x^2| \to 1 \)
\( \displaystyle \lim_{x \to \pm\sqrt{2}} f(x) = \ln(1 - |1 - 2|) = \ln(1 - 1) = \ln(0^+) = -\infty \)
Asintoti verticali:
La retta \( x = 0 \) è asintoto verticale del grafico, poiché \( \displaystyle \lim_{x \to 0} f(x) = -\infty \), anche se il grafico interseca l’asintoto nel punto \( (0,\,0) \).
\( x = -\sqrt{2} \) e \( x = \sqrt{2} \) (estremi del dominio con limite \( -\infty \))
Per \( x \in (-1, 0) \cup (0, 1) \): \( |1 - x^2| = 1 - x^2 \)
\[ f(x) = \ln(1 - (1 - x^2)) = \ln(x^2) = 2\ln|x| \]
Derivata: \( f'(x) = 2 \cdot \frac{1}{x} = \frac{2}{x} \)
Per \( x \in (-\sqrt{2}, -1) \cup (1, \sqrt{2}) \): \( |1 - x^2| = x^2 - 1 \)
\[ f(x) = \ln(1 - (x^2 - 1)) = \ln(2 - x^2) \]
Derivata: \( f'(x) = \frac{-2x}{2 - x^2} \)
| Intervallo | \( f'(x) \) | Monotonia |
|---|---|---|
| \( (-\sqrt{2}, -1) \) | \( + \) | Crescente \( \nearrow \) |
| \( (-1, 0) \) | \( - \) | Decrescente \( \searrow \) |
| \( (0, 1) \) | \( + \) | Crescente \( \nearrow \) |
| \( (1, \sqrt{2}) \) | \( - \) | Decrescente \( \searrow \) |
Derivabilità nei punti \( x = -1 \) e \( x = 1 \):
Studiamo la derivabilità in \( x = 1 \) (per simmetria, il risultato sarà analogo per \( x = -1 \)).
Derivata sinistra in \( x = 1 \):
Per \( x \in (0, 1) \), abbiamo \( f'(x) = \frac{2}{x} \)
\( \displaystyle f'_-(1) = \lim_{x \to 1^-} \frac{2}{x} = 2 \)
Derivata destra in \( x = 1 \):
Per \( x \in (1, \sqrt{2}) \), abbiamo \( f'(x) = \frac{-2x}{2 - x^2} \)
\( \displaystyle f'_+(1) = \lim_{x \to 1^+} \frac{-2x}{2 - x^2} = \frac{-2 \cdot 1}{2 - 1} = \frac{-2}{1} = -2 \)
Poiché \( f'_-(1) = 2 \neq -2 = f'_+(1) \), la funzione non è derivabile in \( x = 1 \).
Analogamente, la funzione non è derivabile in \( x = -1 \) (per simmetria, \( f'_+(−1) = -2 \) e \( f'_-(−1) = 2 \)).
I punti \( x = -1 \) e \( x = 1 \) sono punti angolosi, poiché esistono le derivate destra e sinistra ma sono diverse.
Punti di massimo relativo (e assoluto): \( x = -1 \) e \( x = 1 \) (con \( f(-1) = f(1) = 0 \)). Notiamo che in tali punti la funzione non è derivabile.
Per \( x \in (-1, 0) \cup (0, 1) \):
\[ f''(x) = -\frac{2}{x^2} < 0 \]
Concavità verso il basso.
Per \( x \in (-\sqrt{2}, -1) \cup (1, \sqrt{2}) \):
\[ f''(x) = \frac{-2(2 - x^2) - (-2x)(-2x)}{(2 - x^2)^2} = \frac{-4 + 2x^2 - 4x^2}{(2 - x^2)^2} = \frac{-4 - 2x^2}{(2 - x^2)^2} < 0 \]
Concavità verso il basso.
La funzione ha concavità verso il basso su tutto il dominio.
Grafico della funzione:
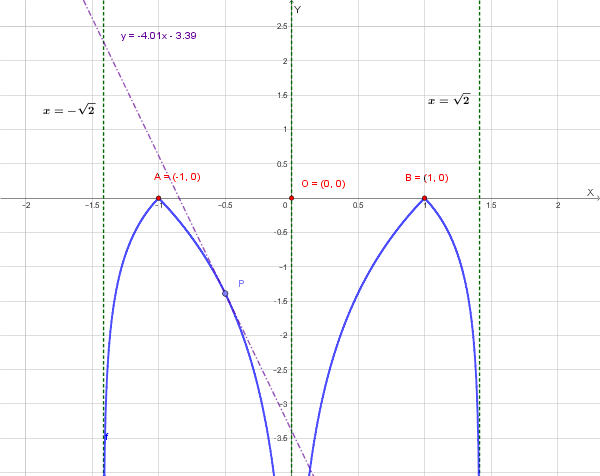
Il punto \( x = -\frac{1}{2} \) appartiene all'intervallo \( (-1, 0) \), quindi:
\[ f\left(-\frac{1}{2}\right) = 2\ln\left|-\frac{1}{2}\right| = 2\ln\left(\frac{1}{2}\right) = 2(-\ln 2) = -2\ln 2 \]
Coefficiente angolare:
\[ f'\left(-\frac{1}{2}\right) = \frac{2}{-\frac{1}{2}} = -4 \]
Equazione della tangente:
\[ y - (-2\ln 2) = -4\left(x - \left(-\frac{1}{2}\right)\right) \] \[ y + 2\ln 2 = -4x - 2 \] \[ y = -4x - 2 - 2\ln 2 \]
Equazione della tangente: \( y = -4x - 2 - 2\ln 2 \)
Il Teorema di Rolle afferma che se una funzione:
allora esiste almeno un punto \( c \in (a, b) \) tale che \( f'(c) = 0 \).
Verifica delle ipotesi:
Continuità in \( [-1, 1] \): La funzione NON è continua in tale intervallo perché non è continua in \( x = 0 \), essendo \( \displaystyle \lim_{x \to 0} f(x) = -\infty \neq f(0) = 0 \)
Conclusione: Il Teorema di Rolle NON è applicabile nell'intervallo \( [-1, 1] \) perché la funzione non è continua nel punto interno in \( x = 0 \).
Considera la funzione:
\[ f(x) = x \cdot \sin(x) \]
a) Calcola la derivata della funzione in \( x = \frac{\pi}{2} \) servendoti della definizione di derivata e verifica il risultato calcolando \( f'\left(\frac{\pi}{2}\right) \) dopo aver calcolato \( f'(x) \) mediante le regole di derivazione.
b) Determina, utilizzando i limiti notevoli, l'ordine di infinitesimo di \( f(x) \) rispetto all'infinitesimo campione \( g(x) = x \) e indica la parte principale di \( f(x) \) rispetto allo stesso infinitesimo campione.
c) Trova gli zeri della funzione.
d) Dai un grafico qualitativo della funzione dopo aver stabilito, mediante un confronto grafico tra funzioni, che f(x) ha infiniti punti stazionari e infiniti flessi.
La funzione da studiare è:
\[ f(x) = x \cdot \sin(x) \]
Metodo 1: Definizione di derivata
Utilizziamo la definizione di derivata:
\[ f'\left(\frac{\pi}{2}\right) = \lim_{h \to 0} \frac{f\left(\frac{\pi}{2} + h\right) - f\left(\frac{\pi}{2}\right)}{h} \]
Calcoliamo i valori necessari:
\( f\left(\frac{\pi}{2}\right) = \frac{\pi}{2} \cdot \sin\left(\frac{\pi}{2}\right) = \frac{\pi}{2} \cdot 1 = \frac{\pi}{2} \)
\( f\left(\frac{\pi}{2} + h\right) = \left(\frac{\pi}{2} + h\right) \cdot \sin\left(\frac{\pi}{2} + h\right) = \left(\frac{\pi}{2} + h\right) \cdot \cos(h) \)
Dove abbiamo usato la formula \( \sin\left(\frac{\pi}{2} + h\right) = \cos(h) \).
Sostituiamo nella definizione:
\[ f'\left(\frac{\pi}{2}\right) = \lim_{h \to 0} \frac{\left(\frac{\pi}{2} + h\right) \cos(h) - \frac{\pi}{2}}{h} \]
Sviluppiamo il numeratore:
\[ = \lim_{h \to 0} \frac{\frac{\pi}{2}\cos(h) + h\cos(h) - \frac{\pi}{2}}{h} = \lim_{h \to 0} \frac{\frac{\pi}{2}[\cos(h) - 1] + h\cos(h)}{h} \]
Separiamo in due limiti:
\[ = \lim_{h \to 0} \frac{\pi}{2} \cdot \frac{\cos(h) - 1}{h} + \lim_{h \to 0} \cos(h) \]
Utilizzando il limite notevole \( \displaystyle \lim_{h \to 0} \frac{\cos(h) - 1}{h} = 0 \) e \( \displaystyle \lim_{h \to 0} \cos(h) = 1 \), otteniamo:
\[ f'\left(\frac{\pi}{2}\right) = \frac{\pi}{2} \cdot 0 + 1 = 1 \]
Metodo 2: Regole di derivazione
Calcoliamo \( f'(x) \) usando la regola del prodotto: \( (u \cdot v)' = u' \cdot v + u \cdot v' \)
\[ f'(x) = (x)' \cdot \sin(x) + x \cdot (\sin(x))' = 1 \cdot \sin(x) + x \cdot \cos(x) = \sin(x) + x\cos(x) \]
Valutiamo in \( x = \frac{\pi}{2} \):
\[ f'\left(\frac{\pi}{2}\right) = \sin\left(\frac{\pi}{2}\right) + \frac{\pi}{2}\cos\left(\frac{\pi}{2}\right) = 1 + \frac{\pi}{2} \cdot 0 = 1 \]
Verifica: I due metodi danno lo stesso risultato: \( f'\left(\frac{\pi}{2}\right) = 1 \)
Studiamo il comportamento di \( f(x) = x\sin(x) \) per \( x \to 0 \), confrontandolo con l'infinitesimo campione \( g(x) = x \).
Osservazione preliminare: La funzione \( f(x) = x\sin(x) \) è pari, infatti:
\[ f(-x) = (-x)\sin(-x) = (-x)(-\sin(x)) = x\sin(x) = f(x) \]
Pertanto, possiamo limitarci a studiare il comportamento per \( x \to 0^+ \), considerando \( x > 0 \). In caso contrario, dovremmo confrontare \( f(x) \) con \( |x|^\alpha \) per tener conto del segno.
Calcoliamo il limite del rapporto:
\[ \lim_{x \to 0^+} \frac{f(x)}{g(x)} = \lim_{x \to 0^+} \frac{x\sin(x)}{x} = \lim_{x \to 0^+} \sin(x) = 0 \]
Poiché il limite è 0, \( f(x) \) è un infinitesimo di ordine superiore rispetto a \( x \).
Determinazione dell'ordine di infinitesimo:
Per determinare l'ordine esatto di infinitesimo di \( f(x) = x\sin(x) \) rispetto a \( x \), cerchiamo \( \alpha \) tale che:
\[ \lim_{x \to 0^+} \frac{f(x)}{x^\alpha} = \lim_{x \to 0^+} \frac{x\sin(x)}{x^\alpha} = \text{finito e diverso da zero} \]
Riscriviamo il limite (per \( x > 0 \)):
\[ \lim_{x \to 0^+} \frac{x\sin(x)}{x^\alpha} = \lim_{x \to 0^+} \frac{\sin(x)}{x^{\alpha-1}} \]
Analizziamo i vari casi confrontando l'esponente \( \alpha - 1 \) con 1:
Se \( \alpha - 1 < 1 \) (cioè \( \alpha < 2 \)): Allora \( x^{\alpha-1} \) tende a zero più lentamente di \( \sin(x) \sim x \). Possiamo scrivere:
\[ \lim_{x \to 0^+} \frac{\sin(x)}{x^{\alpha-1}} = \lim_{x \to 0^+} \frac{\sin(x)}{x} \cdot x^{1-(\alpha-1)} = \lim_{x \to 0^+} \frac{\sin(x)}{x} \cdot x^{2-\alpha} = 1 \cdot \lim_{x \to 0^+} x^{2-\alpha} \]
Poiché \( 2 - \alpha > 0 \), si ha \( \displaystyle \lim_{x \to 0^+} x^{2-\alpha} = 0 \)
\[ \lim_{x \to 0^+} \frac{\sin(x)}{x^{\alpha-1}} = 0 \]
Se \( \alpha - 1 = 1 \) (cioè \( \alpha = 2 \)): Otteniamo esattamente il limite notevole:
\[ \lim_{x \to 0^+} \frac{\sin(x)}{x^{\alpha-1}} = \lim_{x \to 0^+} \frac{\sin(x)}{x} = 1 \quad \text{(limite notevole)} \]
Il limite è finito e diverso da zero! ✓
Se \( \alpha - 1 > 1 \) (cioè \( \alpha > 2 \)): Allora \( x^{\alpha-1} \) tende a zero più velocemente di \( \sin(x) \sim x \). Possiamo scrivere:
\[ \lim_{x \to 0^+} \frac{\sin(x)}{x^{\alpha-1}} = \lim_{x \to 0^+} \frac{\sin(x)}{x} \cdot \frac{x}{x^{\alpha-1}} = \lim_{x \to 0^+} \frac{\sin(x)}{x} \cdot \frac{1}{x^{\alpha-2}} = 1 \cdot \lim_{x \to 0^+} \frac{1}{x^{\alpha-2}} \]
Poiché \( \alpha - 2 > 0 \), si ha \( \displaystyle \lim_{x \to 0^+} \frac{1}{x^{\alpha-2}} = +\infty \)
\[ \lim_{x \to 0^+} \frac{\sin(x)}{x^{\alpha-1}} = +\infty \]
Risultato: Il valore di \( \alpha \) che rende il limite finito e diverso da zero è \( \alpha = 2 \).
Verifica esplicita con \( \alpha = 2 \):
\[ \lim_{x \to 0^+} \frac{x\sin(x)}{x^2} = \lim_{x \to 0^+} \frac{\sin(x)}{x} = 1 \]
Conclusione: \( f(x) = x\sin(x) \) è un infinitesimo di ordine 2 rispetto a \( x \).
La parte principale è: \( x^2 \) (poiché \( \displaystyle \lim_{x \to 0} \frac{x\sin(x)}{x^2} = 1 \), si ha \( x\sin(x) \sim x^2 \) per \( x \to 0 \))
Cerchiamo i valori di \( x \) per cui \( f(x) = 0 \):
\[ x \cdot \sin(x) = 0 \]
Questa equazione è soddisfatta quando:
\( x = 0 \), oppure
\( \sin(x) = 0 \), cioè quando \( x = k\pi \) con \( k \in \mathbb{Z} \)
Zeri della funzione: \( x = k\pi \) con \( k \in \mathbb{Z} \)
(cioè: \( \ldots, -2\pi, -\pi, 0, \pi, 2\pi, 3\pi, \ldots \))
Studio della derivata prima:
Abbiamo già calcolato: \( f'(x) = \sin(x) + x\cos(x) \)
I punti stazionari si trovano risolvendo \( f'(x) = 0 \):
\[ \sin(x) + x\cos(x) = 0 \]
Analisi dell'equazione:
Caso 1: \( \cos(x) = 0 \)
Se \( \cos(x) = 0 \), allora \( x = \frac{\pi}{2} + k\pi \) con \( k \in \mathbb{Z} \).
In questi punti, l'equazione \( f'(x) = 0 \) diventa:
\[ \sin(x) + x \cdot 0 = 0 \quad \Rightarrow \quad \sin(x) = 0 \]
Ma dove \( \cos(x) = 0 \), si ha \( \sin(x) = \pm 1 \neq 0 \). Quindi non esistono soluzioni in questo caso.
Caso 2: \( \cos(x) \neq 0 \)
Possiamo dividere l'equazione \( \sin(x) + x\cos(x) = 0 \) per \( \cos(x) \):
\[ \frac{\sin(x)}{\cos(x)} + x = 0 \quad \Rightarrow \quad \tan(x) = -x \]
Studiamo l'equazione \( \tan(x) = -x \) analizzando graficamente le intersezioni tra \( y = \tan(x) \) e \( y = -x \)
Confronto grafico:
Rappresentiamo graficamente nello stesso piano cartesiano le funzioni \( y = \tan(x) \) e \( y = -x \):
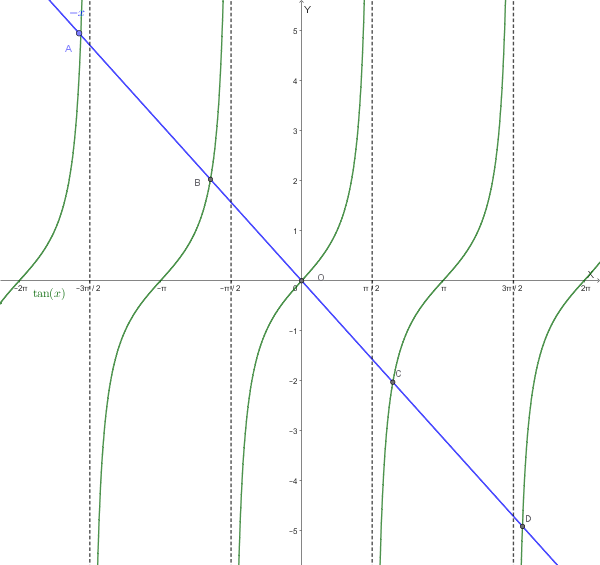
Dal grafico si evince che:
Le due curve si intersecano nell'origine \( (0, 0) \)
In ogni intervallo \( \left(-\frac{\pi}{2} - k\pi, \frac{\pi}{2} + k\pi\right) \) con \( k \in \mathbb{Z} \setminus \{0\} \), la tangente attraversa tutti i valori reali, mentre la retta \( y = -x \) è monotona, quindi esiste esattamente un punto di intersezione
Poiché entrambe le funzioni sono dispari (\( \tan(-x) = -\tan(x) \) e \( -(-x) = x \)), le intersezioni sono simmetriche rispetto all'origine
Dal grafico si deduce anche che a sinistra e a destra degli zeri della derivata prima cambia il suo segno, quindi avremmo infiniti massimi e infiniti minimi relativi
Conclusione: L'equazione \( \tan(x) = -x \) ha infinite soluzioni, quindi \( f'(x) = 0 \) in infiniti punti. La funzione \( f(x) = x\sin(x) \) ha infiniti punti stazionari, che sono massimi o minimi relativi..
Derivata seconda:
Calcoliamo la derivata seconda di \( f(x) = x\sin(x) \):
\[ f''(x) = \frac{d}{dx}[\sin(x) + x\cos(x)] = \cos(x) + \cos(x) - x\sin(x) = 2\cos(x) - x\sin(x) \]
I punti di flesso si trovano risolvendo \( f''(x) = 0 \):
\[ 2\cos(x) - x\sin(x) = 0 \]
Analisi dell'equazione:
Caso 1: \( \sin(x) = 0 \)
Se \( \sin(x) = 0 \), allora \( x = k\pi \) con \( k \in \mathbb{Z} \).
In questi punti, l'equazione \( f''(x) = 0 \) diventa:
\[ 2\cos(x) - x \cdot 0 = 0 \quad \Rightarrow \quad \cos(x) = 0 \]
Ma dove \( \sin(x) = 0 \) (cioè \( x = k\pi \)), si ha \( \cos(x) = \pm 1 \neq 0 \). Quindi non esistono soluzioni in questo caso.
Caso 2: \( \sin(x) \neq 0 \)
Possiamo riscrivere l'equazione \( 2\cos(x) - x\sin(x) = 0 \) come:
\[ 2\cos(x) = x\sin(x) \]
Dividendo per \( \sin(x) \) (che è diverso da zero):
\[ \frac{2\cos(x)}{\sin(x)} = x \quad \Rightarrow \quad 2\cot(x) = x \]
Studiamo l'equazione \( \cot(x) = \frac{x}{2} \) mediante un confronto grafico analizzando le intersezioni tra \( y = \cot(x) \) e \( y = \frac{x}{2} \):
Confronto grafico:
Rappresentiamo graficamente nello stesso piano cartesiano le funzioni \( y = \cot(x) \) e \( y = \frac{x}{2} \):
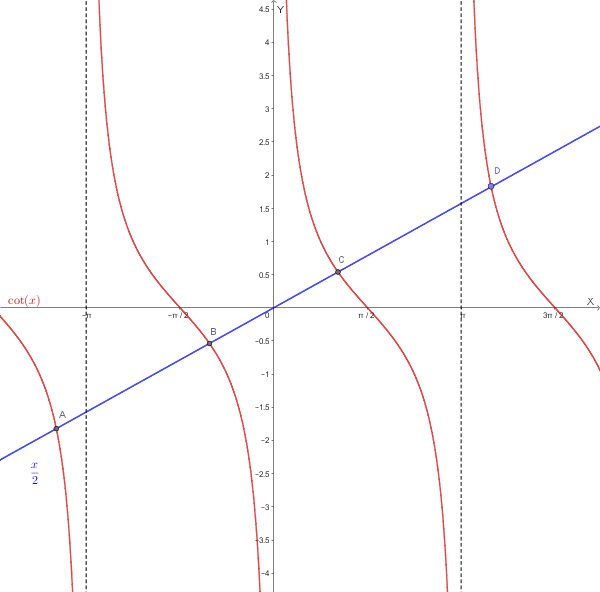
Dal grafico si evince che:
La funzione \( \cot(x) \) è definita negli intervalli \( (k\pi, (k+1)\pi) \) con \( k \in \mathbb{Z} \), dove decresce da \( +\infty \) a \( -\infty \)
La retta \( y = \frac{x}{2} \) ha pendenza \( \frac{1}{2} \) e passa per l'origine
In ogni intervallo \( (k\pi, (k+1)\pi) \) con \( k \neq 0 \), la cotangente attraversa tutti i valori reali, mentre la retta \( y = \frac{x}{2} \) è monotona crescente, quindi esiste esattamente un punto di intersezione
Poiché entrambe le funzioni sono dispari (\( \cot(-x) = -\cot(x) \) e \( \frac{-x}{2} = -\frac{x}{2} \)), le intersezioni sono simmetriche rispetto all'origine
Dal grafico si deduce anche che a sinistra e a destra degli zeri della derivata seconda cambia il suo segno, quindi avremo infiniti flessi
Conclusione: L'equazione \( \cot(x) = \frac{x}{2} \) ha infinite soluzioni, quindi \( f''(x) = 0 \) in infiniti punti. La funzione \( f(x) = x\sin(x) \) ha infiniti punti di flesso.
Caratteristiche della funzione:
Comportamento agli estremi:
Per \( x \to +\infty \) e per \( x \to -\infty \) la funzione oscilla con ampiezza crescente
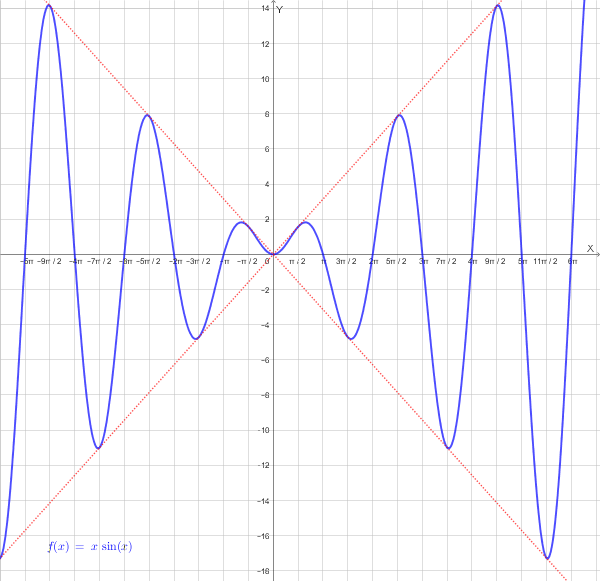
Grafico qualitativo:
Il grafico mostra la funzione \( f(x) = x\sin(x) \) che oscilla con ampiezza crescente, attraversando l'asse x nei multipli di \( \pi \), con infiniti massimi e minimi relativi e infiniti flessi.
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.