



Questo compito è stato assegnato il 27 novembre 1986 a una classe 5ª del Liceo Scientifico.
Argomenti: Calcolo di limiti, Limiti in funzione di un parametro, grafico qualitativo di una funzione, proprietà dei limiti, grafico probabile di una funzione.
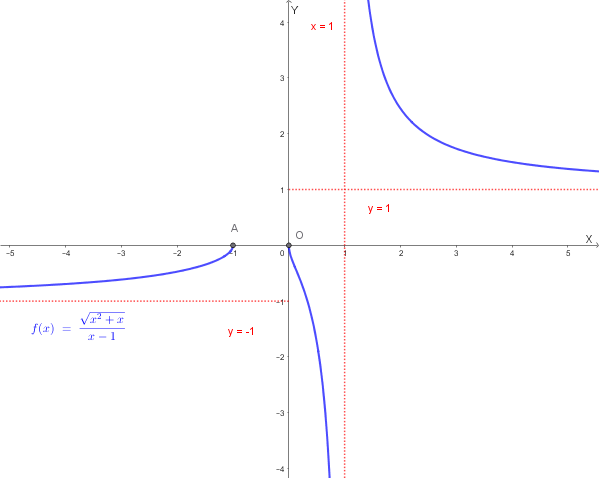
Tracciare un grafico qualitativo della seguente funzione:
\[ y = f(x) = \frac{\sqrt{x^2+x}}{x-1} \]Sono richiesti:
2. Parità e disparità:
Non essendo il dominio simmetrico rispetto all'origine, la funzione non può essere né pari né dispari.
Per verificare la parità o disparità in base alla definizione, calcoliamo \( f(-x) \):
\[ f(-x) = \frac{\sqrt{(-x)^2+(-x)}}{(-x)-1} = \frac{\sqrt{x^2-x}}{-x-1} \]
Poiché \( f(-x) \neq f(x) \) e \( f(-x) \neq -f(x) \), la funzione non è né pari né dispari.
5. Limiti agli estremi del dominio:
\[ \lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} \frac{\sqrt{1+1}}{x-1} = \lim_{x \to 1^-} \frac{\sqrt{2}}{x-1} = -\infty \]
\[ \lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} \frac{\sqrt{1+1}}{x-1} = \lim_{x \to 1^+} \frac{\sqrt{2}}{x-1} = +\infty \]
\[ \lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \frac{\sqrt{x^2+x}}{x-1} = \lim_{x \to -\infty} \frac{|x|\sqrt{1+\frac{1}{x}}}{x-1} = \lim_{x \to -\infty} \frac{-x\sqrt{1+\frac{1}{x}}}{x-1} = \lim_{x \to -\infty} \frac{-x}{x} = -1 \]
\[ \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \frac{\sqrt{x^2+x}}{x-1} = \lim_{x \to +\infty} \frac{x\sqrt{1+\frac{1}{x}}}{x-1} = \lim_{x \to +\infty} \frac{x}{x} = 1 \]
7. Intersezioni con gli asintoti:
Con l'asintoto \( y = -1 \):
\( \frac{\sqrt{x^2+x}}{x-1} = -1 \)
\( \sqrt{x^2+x} = -(x-1) = 1-x \)
Per \( x < 1 \): \( x^2+x = (1-x)^2 = 1-2x+x^2 \)
\( x = 1-2x \implies 3x = 1 \implies x = \frac{1}{3} \)
Tuttavia, \( x = \frac{1}{3} \in [0,1) \), che non appartiene al ramo dove vale l'asintoto \( y = -1 \) (cioè \( x \in (-\infty, -1] \)).
Pertanto, non c'è intersezione con l'asintoto \( y = -1 \).
Con l'asintoto \( y = 1 \):
\( \frac{\sqrt{x^2+x}}{x-1} = 1 \)
\( \sqrt{x^2+x} = x-1 \)
Per \( x > 1 \): \( x^2+x = (x-1)^2 = x^2-2x+1 \)
\( x = -2x+1 \implies 3x = 1 \implies x = \frac{1}{3} \)
Ma \( \frac{1}{3} \not> 1 \), quindi non c'è intersezione con questo asintoto.
Per dimostrare che una funzione non è limitata, dobbiamo mostrare che non esiste un numero reale \( M \) tale che \( |f(x)| \leq M \) per ogni \( x \) nel dominio della funzione.
Dalla definizione di limite, sappiamo che se \( \lim_{x \to 1} f(x) = -\infty \), allora per ogni numero reale \( K < 0 \) esiste un intorno di 1, diciamo \( I(1) \), tale che per ogni \( x \in I(1) \) (con \( x \neq 1 \)), si ha \( f(x) < K \).
Prendiamo un qualsiasi \( M > 0 \). Possiamo scegliere \( K = -M \), che è negativo. Dalla condizione precedente, esiste un intorno \( I(1) \) tale che per \( x \in I(1) \) (con \( x \neq 1 \)) si ha \( f(x) < -M \), cioè \( f(x) < -M < 0 \).
Questo significa che \( |f(x)| = -f(x) > M \) per tali valori di \( x \).
Poiché questo vale per ogni \( M > 0 \), non esiste alcun valore finito \( M \) che possa limitare superiormente \( |f(x)| \). Di conseguenza, la funzione \( f(x) \) non è limitata.
Calcolare i seguenti limiti:
a) \(\lim_{x \to 1} \frac{x^2+|x-1|-1}{x-1}\)
Per risolvere questo limite, dobbiamo considerare il valore assoluto \(|x-1|\). Studiamo i due casi separatamente.
Caso 1: \(x > 1\), quindi \(|x-1| = x-1\)
\[ \lim_{x \to 1^+} \frac{x^2+(x-1)-1}{x-1} = \lim_{x \to 1^+} \frac{x^2+x-2}{x-1} \]
Fattorizziamo il numeratore: \(x^2+x-2 = (x+2)(x-1)\)
\[ = \lim_{x \to 1^+} \frac{(x+2)(x-1)}{x-1} = \lim_{x \to 1^+} (x+2) = 1+2 = 3 \]
Caso 2: \(x < 1\), quindi \(|x-1| = -(x-1) = 1-x\)
\[ \lim_{x \to 1^-} \frac{x^2+(1-x)-1}{x-1} = \lim_{x \to 1^-} \frac{x^2-x}{x-1} = \lim_{x \to 1^-} \frac{x(x-1)}{x-1} \]
\[ = \lim_{x \to 1^-} x = 1 \]
Poiché \(\lim_{x \to 1^+} f(x) = 3 \neq 1 = \lim_{x \to 1^-} f(x)\), il limite non esiste.
b) \(\lim_{x \to \frac{\pi}{6}^+} \left(\frac{1}{2}\right)^{\frac{1}{1-2\sin(x)}}\)
Analizziamo prima il comportamento dell'esponente quando \(x \to \frac{\pi}{6}^+\).
Sappiamo che \(\sin\left(\frac{\pi}{6}\right) = \frac{1}{2}\), quindi \(1-2\sin\left(\frac{\pi}{6}\right) = 1-2 \cdot \frac{1}{2} = 0\).
Per \(x > \frac{\pi}{6}\) e vicino a \(\frac{\pi}{6}\), abbiamo \(\sin(x) > \sin\left(\frac{\pi}{6}\right) = \frac{1}{2}\) (dato che \(\sin(x)\) è crescente in questo intervallo).
Quindi \(2\sin(x) > 1\), il che implica \(1-2\sin(x) < 0\).
Quando \(x \to \frac{\pi}{6}^+\), abbiamo \(1-2\sin(x) \to 0^-\), quindi \(\frac{1}{1-2\sin(x)} \to -\infty\).
Il limite diventa:
\[ \lim_{x \to \frac{\pi}{6}^+} \left(\frac{1}{2}\right)^{\frac{1}{1-2\sin(x)}} \]
Poiché \(0 < \frac{1}{2} < 1\) e l'esponente tende a \(-\infty\), abbiamo:
\[ \left(\frac{1}{2}\right)^{-\infty} = \frac{1}{\left(\frac{1}{2}\right)^{+\infty}} = \frac{1}{0^+} = +\infty \]
Quindi il limite è \(+\infty\).
c) \(\lim_{x \to +\infty} \left(\frac{1+x}{2+x}\right)^{x}\)
Si tratta di una forma indeterminata del tipo \(1^{\infty}\). Per risolverla, trasformiamo la base per riconduirci al limite notevole \(\lim_{t \to +\infty} \left(1+\frac{1}{t}\right)^t = e\).
Riscriviamo la base:
\[ \frac{1+x}{2+x} = \frac{1+x}{1+x+1} = \frac{1+x}{(1+x)+1} = \frac{1}{1+\frac{1}{1+x}} \]
Quindi:
\[ \left(\frac{1+x}{2+x}\right)^{x} = \left(\frac{1}{1+\frac{1}{1+x}}\right)^{x} = \frac{1}{\left(1+\frac{1}{1+x}\right)^{x}} \]
Ora dobbiamo calcolare:
\[ \lim_{x \to +\infty} \left(1+\frac{1}{1+x}\right)^{x} \]
Riscriviamo l'esponente in modo da applicare il limite notevole. Poniamo \(t = 1+x\), quindi per \(x \to +\infty\) abbiamo \(t \to +\infty\) e \(x = t-1\):
\[ \left(1+\frac{1}{1+x}\right)^{x} = \left(1+\frac{1}{t}\right)^{t-1} = \left(1+\frac{1}{t}\right)^{t} \cdot \left(1+\frac{1}{t}\right)^{-1} \]
Per \(t \to +\infty\):
\[ \lim_{t \to +\infty} \left(1+\frac{1}{t}\right)^{t} = e \]
\[ \lim_{t \to +\infty} \left(1+\frac{1}{t}\right)^{-1} = 1 \]
Quindi:
\[ \lim_{x \to +\infty} \left(1+\frac{1}{1+x}\right)^{x} = e \cdot 1 = e \]
Pertanto:
\[ \lim_{x \to +\infty} \left(\frac{1+x}{2+x}\right)^{x} = \frac{1}{e} = e^{-1} \]
Per quale valore del parametro reale \(a\) risulta:
\[ \lim_{x \to 1} \frac{1-x^2}{x^2+ax-1-a} = \frac{1}{3} \]Per determinare il valore del parametro \(a\), analizziamo prima il comportamento del numeratore e del denominatore quando \(x \to 1\).
Numeratore:
\[ \lim_{x \to 1} (1-x^2) = 1-1^2 = 0 \]
Denominatore:
\[ \lim_{x \to 1} (x^2+ax-1-a) = 1^2+a \cdot 1-1-a = 1+a-1-a = 0 \]
Il denominatore si annulla sempre per \(x = 1\), indipendentemente dal valore di \(a\).
Poiché sia il numeratore che il denominatore tendono a zero, abbiamo una forma indeterminata \(\frac{0}{0}\). Scomponiamo numeratore e denominatore:
Fattorizzazione
Fattorizziamo il numeratore:
\[ 1-x^2 = (1-x)(1+x) \]
Per il denominatore, osserviamo che si annulla per \(x = 1\), quindi \((x-1)\) è un fattore:
\[ x^2+ax-1-a = x^2-1+ax-a=(x-1)(x+1)+a(x-1)=(x-1)(x+1+a) \]
Il limite diventa: \[ \lim_{x \to 1} \frac{(1-x)(1+x)}{(x-1)(x+1+a)} = \lim_{x \to 1} \frac{-(x-1)(1+x)}{(x-1)(x+1+a)} \] Semplificando \((x-1)\): \[ = \lim_{x \to 1} \frac{-(1+x)}{x+1+a} = \frac{-(1+1)}{1+1+a} = \frac{-2}{2+a} \]
Condizione:
Affinché il limite sia uguale a \(\frac{1}{3}\), deve valere:
\[ \frac{-2}{2+a} = \frac{1}{3} \]
Risolviamo l'equazione:
\[ -2 \cdot 3 = 1 \cdot (2+a) \]
\[ -6 = 2+a \]
\[ a = -8 \]
Verifica:
Con \(a = -8\), il limite diventa:
\[ \lim_{x \to 1} \frac{1-x^2}{x^2-8x-1+8} = \lim_{x \to 1} \frac{1-x^2}{x^2-8x+7} \]
Fattorizzando: \(x^2-8x+7 = (x-1)(x-7)\)
\[ = \lim_{x \to 1} \frac{(1-x)(1+x)}{(x-1)(x-7)} = \lim_{x \to 1} \frac{-(1+x)}{x-7} = \frac{-2}{1-7} = \frac{-2}{-6} = \frac{1}{3} \] ✓
Risposta: Il valore del parametro è \(\boxed{a = -8}\).
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.