



Questo compito è stato assegnato il giorno 03 Ottobre 1987 a una classe 5ª del Liceo Scientifico.
Argomenti: Funzioni deducibili, dimostrazione della monotonia di una funzione con la definizione, funzione inversa, insiemi numerici
(estremo superiore e inferiore, massimo e minimo, punti di accumulazione).
Data la funzione \[f(x)=\frac{\sin(x)\cos(x)}{\cos(2x)}\] dimostrare che è periodica, trovare il periodo T e rappresentarla graficamente in un periodo a partire da funzioni note.
Passo 1: Semplificazione della funzione
Utilizziamo la formula di duplicazione del seno, \( \sin(2x) = 2\sin(x)\cos(x) \), per semplificare il numeratore:
\[ \sin(x)\cos(x) = \frac{1}{2}\sin(2x) \]
Sostituendo nella funzione originale, otteniamo:
\[ f(x) = \frac{\frac{1}{2}\sin(2x)}{\cos(2x)} = \frac{1}{2}\frac{\sin(2x)}{\cos(2x)} = \frac{1}{2}\tan(2x) \]Passo 2: Dimostrazione della periodicità e calcolo del periodo
Una funzione \(f(x)\) si dice periodica di periodo \(T\) se \(f(x+T) = f(x)\). La funzione tangente \(y = \tan(x)\) ha periodo \(T = \pi\). Una funzione del tipo \(y = \tan(kx)\) ha periodo \(T = \frac{\pi}{|k|}\).
Nel nostro caso, \(f(x) = \frac{1}{2}\tan(2x)\), con \(k = 2\). Pertanto, il periodo è:
\[ T = \frac{\pi}{|2|} = \frac{\pi}{2} \]Dimostriamo che \(f\left(x + \frac{\pi}{2}\right) = f(x)\):
\[ f\left(x + \frac{\pi}{2}\right) = \frac{1}{2}\tan\left(2\left(x + \frac{\pi}{2}\right)\right) = \frac{1}{2}\tan(2x + \pi) \]Poiché la tangente è periodica con periodo \(\pi\), sappiamo che \( \tan(2x + \pi) = \tan(2x) \). Quindi:
\[ f\left(x + \frac{\pi}{2}\right) = \frac{1}{2}\tan(2x) = f(x) \]La funzione è periodica di periodo \(T = \frac{\pi}{2}\).
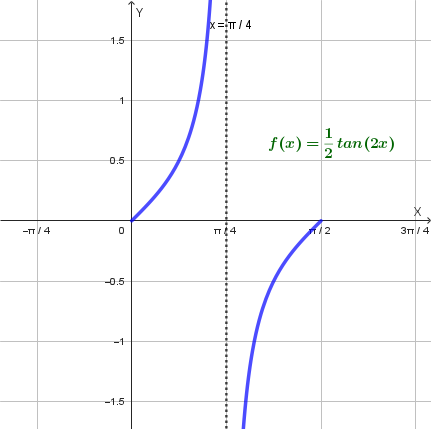
Passo 3: Rappresentazione grafica
Il grafico di \(f(x) = \frac{1}{2}\tan(2x)\) si ottiene dal grafico di base \(y = \tan(x)\) attraverso due trasformazioni:
Il grafico della funzione \(f(x) = \frac{1}{2}\tan(2x)\) è il seguente:
Dimostrare che se \(f(x)\) e \(g(x)\) sono crescenti nell'intervallo \((a; b)\) allora anche la funzione \(h(x)=f(x)+g(x)\) è crescente in tale intervallo. Fornire un esempio grafico di questa proprietà.
Dimostrazione:
Per definizione, una funzione si dice **crescente** in un intervallo se per ogni coppia di punti \(x_1, x_2\) in quell'intervallo, con \(x_1 < x_2\), si ha che \(f(x_1) \le f(x_2)\).
Prendiamo due punti qualsiasi \(x_1, x_2\) nell'intervallo \((a; b)\) tali che \(x_1 < x_2\).
Poiché \(f(x)\) è crescente, per definizione abbiamo:
\[f(x_1) \le f(x_2)\]Allo stesso modo, poiché anche \(g(x)\) è crescente, abbiamo:
\[g(x_1) \le g(x_2)\]Sommando membro a membro le due disuguaglianze, otteniamo:
\[f(x_1) + g(x_1) \le f(x_2) + g(x_2)\]Considerando la funzione \(h(x) = f(x) + g(x)\), possiamo riscrivere l'espressione come:
\[h(x_1) \le h(x_2)\]Questo dimostra che, se prendiamo due punti qualsiasi \(x_1 < x_2\), l'ordinata di \(h(x_1)\) è minore o uguale a quella di \(h(x_2)\). Pertanto, la funzione somma \(h(x)\) è crescente nell'intervallo \((a; b)\).
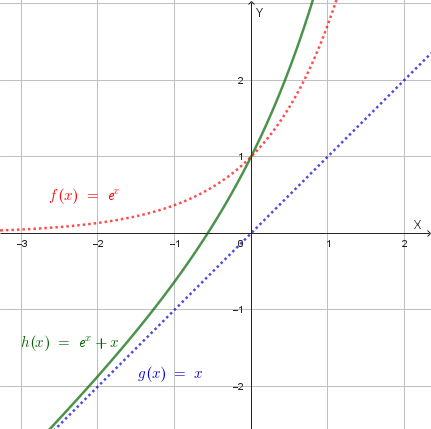
Esempio grafico:
Consideriamo due funzioni crescenti nell'intervallo \((-\infty, +\infty)\):
La loro somma è la funzione \(h(x) = f(x) + g(x) = e^x + x\). Come si può vedere dal grafico, la somma delle due funzioni è anch'essa una funzione crescente.
Data la funzione \(y=f(x)=\arcsin(x-1)\):
a) determinare il dominio
b) dimostrare che è invertibile
c) tracciare il grafico della funzione data
d) risolvere l'equazione \(f(x)=\frac{\pi}{6}\)
e) indicata con \(g(x)\) la funzione inversa, rappresentarla graficamente.
a) Dominio
Il dominio della funzione arcoseno, \(y = \arcsin(z)\), è l'intervallo \([-1, 1]\). Per determinare il dominio della nostra funzione, dobbiamo imporre che l'argomento \(x-1\) sia compreso in tale intervallo:
\[-1 \le x-1 \le 1\]Sommando 1 a tutti i membri della disequazione, otteniamo il dominio della funzione:
\[0 \le x \le 2\]Il dominio è l'intervallo chiuso \([0, 2]\).
b) Invertibilità
Se una funzione è **monotona** (cioè strettamente crescente o strettamente decrescente) nel suo dominio, allora è invertibile. La funzione \(f(x) = \arcsin(x-1)\) è la composizione di due funzioni: una funzione lineare \(g(x) = x-1\), che è strettamente crescente, e la funzione arcoseno \(h(z) = \arcsin(z)\), che è anch'essa strettamente crescente nel suo dominio \([-1, 1]\). La composizione di funzioni strettamente crescenti è una funzione strettamente crescente. Quindi, la funzione data è strettamente crescente e, di conseguenza, invertibile.
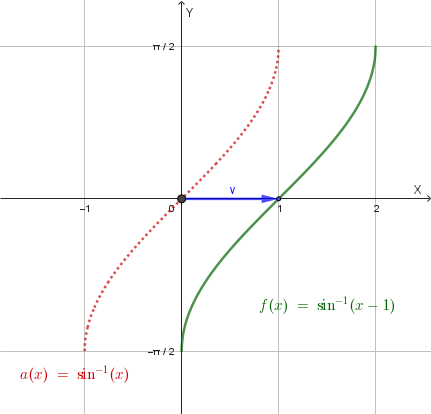
c) Grafico della funzione
Il grafico di \(y = \arcsin(x-1)\) si ottiene per traslazione orizzontale del grafico di \(y = \arcsin(x)\) di una unità verso destra. Il punto centrale \((0, 0)\) del grafico di base si sposta nel punto \((1, 0)\). Il grafico è il seguente:
d) Risoluzione dell'equazione \(f(x) = \frac{\pi}{6}\)
Dobbiamo risolvere l'equazione \( \arcsin(x-1) = \frac{\pi}{6} \). Applicando il seno a entrambi i membri, otteniamo:
\[ \sin(\arcsin(x-1)) = \sin\left(\frac{\pi}{6}\right) \] \[ x-1 = \frac{1}{2} \]Risolvendo per \(x\):
\[ x = 1 + \frac{1}{2} = \frac{3}{2} \]Il valore \(x = \frac{3}{2} = 1.5\) rientra nel dominio \([0, 2]\) della funzione, quindi la soluzione è valida.
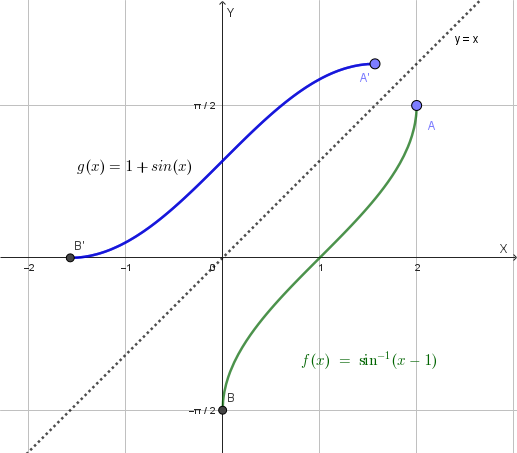
e) Grafico della funzione inversa
Per trovare la funzione inversa, \(y = g(x)\), partiamo dalla funzione data e scambiamo le variabili \(x\) e \(y\):
\[ x = \arcsin(y-1) \]Applichiamo il seno a entrambi i membri per isolare \(y\):
\[ \sin(x) = y-1 \] \[ y = \sin(x) + 1 \]Quindi, la funzione inversa è \(g(x) = \sin(x) + 1\). Il suo dominio è il codominio della funzione di partenza, ovvero l'intervallo \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\).
Il grafico di \(g(x) = \sin(x) + 1\) si ottiene con una traslazione verticale del grafico di \(y = \sin(x)\) di una unità verso l'alto, ristretto all'intervallo \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\), oppure (in base alla proprietà generale del grafico della funzione inversa) mediante una simmetria del grafico della funzione \(y=f(x)=\arcsin(x-1)\) rispetto alla retta \(y=x\).
Si consideri il seguente insieme di numeri reali:
\[E=\left\{x \in \mathbb{R} \mid x=\frac{(-1)^{n+1}(2n-1)}{n}, \text{ con } n \in \mathbb{N}, \text{ ed } n \neq 0\right\}\]
a) Determinare l'estremo inferiore e l'eventuale minimo
b) Determinare l'estremo superiore e l'eventuale massimo
c) Trovare gli eventuali punti di accumulazione.
L'insieme \(E\) è costituito da valori generati dalla formula \( x_n = \frac{(-1)^{n+1}(2n-1)}{n} \). Analizzando la formula, possiamo dividere i termini in due successioni, una per \(n\) pari e una per \(n\) dispari.
Ecco i primi valori della successione:
| n | Formula | Valore \(x_n\) |
|---|---|---|
| 1 | \(\frac{(-1)^{2}(1)}{1}\) | 1 |
| 2 | \(\frac{(-1)^{3}(3)}{2}\) | -1.5 |
| 3 | \(\frac{(-1)^{4}(5)}{3}\) | \(\approx\) 1.66 |
| 4 | \(\frac{(-1)^{5}(7)}{4}\) | -1.75 |
| 5 | \(\frac{(-1)^{6}(9)}{5}\) | 1.8 |
| 6 | \(\frac{(-1)^{7}(11)}{6}\) | \(\approx\) -1.83 |
Analisi per \(n\) dispari:
Se \(n\) è dispari, i termini sono positivi e si avvicinano a 2 da sinistra. La successione è \(x_n = 2 - \frac{1}{n}\).
Analisi per \(n\) pari:
Se \(n\) è pari, i termini sono negativi e si avvicinano a -2 da destra. La successione è \(x_n = -2 + \frac{1}{n}\).
a) Estremo inferiore e minimo:
L'estremo inferiore è **-2**. Non esiste un minimo, poiché la successione si avvicina a -2 ma non lo raggiunge mai.
b) Estremo superiore e massimo:
L'estremo superiore è **2**. Non esiste un massimo, in quanto la successione si avvicina a 2 ma non lo raggiunge mai.
c) Punti di accumulazione:
I punti di accumulazione sono i valori a cui le successioni convergono. Nel nostro caso, l'insieme ha due punti di accumulazione: **-2** e **2**.
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.