



Questo compito è stato assegnato nel mese di Novembre 1988 a una classe 5ª del Liceo Scientifico.
Argomenti: Problema con calcolo di limite, Discussione limite in funzione di un parametro, Grafico qualitativo di una funzione, ordine di un infinitesimo e parte principale, calcolo di limiti.
In una circonferenza di raggio \(R\) è condotta la corda \(AB\) la cui misura è \(R\sqrt{3}\). Sul maggiore dei due archi \(AB\) si prenda un punto \(D\) e sia \(AC\) la bisettrice dell'angolo \(\widehat{BAD}\). Calcolare il seguente limite:
\[\lim_{D \to B} \frac{BD \cdot AC}{BC \cdot AD}\]
Analisi della configurazione geometrica
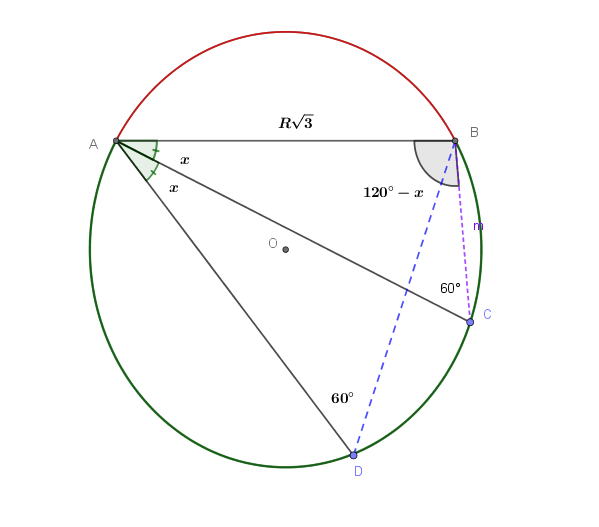
La corda \(AB\) ha lunghezza \(R\sqrt{3}\), che corrisponde al lato del triangolo equilatero inscritto nella circonferenza di raggio \(R\).
Pertanto, gli angoli alla circonferenza che insistono sull'arco minore \(AB\) misurano tutti \(60°\). In particolare:
Impostazione del problema
Sia \(AC\) la bisettrice dell'angolo \(\widehat{BAD}\). Poniamo:
\[\widehat{CAB} = \widehat{DAC} = x\]
Quindi \(\widehat{BAD} = 2x\).
Comportamento al limite
Quando \(D \to B\), l'angolo \(\widehat{BAD} \to 0\), quindi \(x \to 0\).
In questa situazione limite:
Pertanto, nel calcolo del limite, i termini \(AC\) e \(AD\) si semplificano:
\[\lim_{D \to B} \frac{BD \cdot AC}{BC \cdot AD} = \lim_{x \to 0} \frac{BD \cdot AC}{BC \cdot AD} = \lim_{x \to 0} \frac{BD}{BC} \cdot \frac{AC}{AD} = \lim_{x \to 0} \frac{BD}{BC} \cdot 1 = \lim_{x \to 0} \frac{BD}{BC}\]
Calcolo delle corde con il teorema della corda
Utilizziamo il teorema della corda: in una circonferenza di raggio \(R\), la corda che sottende un angolo al centro \(\alpha\) ha lunghezza \(2R\sin\left(\frac{\alpha}{2}\right)\).
Per la corda \(BD\): l'angolo \(\widehat{BAD} = 2x\), quindi:
\[BD = 2R\sin(2x)\]
Per la corda \(BC\): l'angolo \(\widehat{BAC} = x\), quindi:
\[BC = 2R\sin(x)\]
Calcolo del limite
Sostituendo le espressioni trovate:
Quindi:
\[\lim_{x \to 0} \frac{BD}{BC} = \lim_{x \to 0} \frac{2R\sin(2x)}{2R\sin(x)} = \lim_{x \to 0} \frac{\sin(2x)}{\sin(x)} = \lim_{x \to 0} \frac{2\sin(x)\cos(x)}{\sin(x)} = \lim_{x \to 0} 2\cos(x) = 2\]
Risultato finale:
\[\lim_{D \to B} \frac{BD \cdot AC}{BC \cdot AD} = 2\]
Calcolare, al variare del parametro reale \(a>0\), il seguente limite:
\[ \lim_{x \to +\infty} \left(\frac{6ax+1}{3x-2}\right)^x \]
Passo 1: Calcolo del limite della base
Calcoliamo prima il limite della base della potenza:
\[ \lim_{x \to +\infty} \frac{6ax+1}{3x-2} = \lim_{x \to +\infty} \frac{6ax\left(1+\frac{1}{6ax}\right)}{3x\left(1-\frac{2}{3x}\right)} = \frac{6a}{3} = 2a \]
Passo 2: Valutazione del risultato
Passo 3: Analisi del caso \(a = \frac{1}{2}\)
Quando \(a = \frac{1}{2}\), la funzione diventa:
\[ \frac{6 \cdot \frac{1}{2} \cdot x + 1}{3x-2} = \frac{3x+1}{3x-2} \]
Possiamo riscrivere questa espressione come:
\[ \frac{3x+1}{3x-2} = \frac{3x-2+3}{3x-2} = 1 + \frac{3}{3x-2} \]
Quindi il limite diventa:
\[ \lim_{x \to +\infty} \left(1 + \frac{3}{3x-2}\right)^x \]
Passo 4: Trasformazione dell'esponente
Per utilizzare il limite notevole \(\displaystyle \lim_{t \to +\infty} \left(1 + \frac{1}{t}\right)^t = e\), dobbiamo trasformare l'esponente in modo che compaia \(\frac{3x-2}{3}\):
\[ \left(1 + \frac{3}{3x-2}\right)^x = \left(1 + \frac{3}{3x-2}\right)^{\frac{3x-2}{3} \cdot \frac{3x}{3x-2}} \]
Possiamo riscrivere come:
\[ \left[\left(1 + \frac{3}{3x-2}\right)^{\frac{3x-2}{3}}\right]^{\frac{3x}{3x-2}} \]
Passo 5: Sostituzione e calcolo del limite
Poniamo \(t = \frac{3x-2}{3}\). Quando \(x \to +\infty\), anche \(t \to +\infty\).
Calcoliamo separatamente i due limiti:
Limite della base:
\[ \lim_{t \to +\infty} \left(1 + \frac{1}{t}\right)^{t} = e \]
Limite dell'esponente:
\[ \lim_{x \to +\infty} \frac{3x}{3x-2} = \lim_{x \to +\infty} \frac{3x-2+2}{3x-2} = \lim_{x \to +\infty} \left(1 + \frac{2}{3x-2}\right) = 1 \]
Applicando le proprietà dei limiti:
\[ \lim_{x \to +\infty} \left[\left(1 + \frac{3}{3x-2}\right)^{\frac{3x-2}{3}}\right]^{\frac{3x}{3x-2}} = \left[\lim_{t \to +\infty} \left(1 + \frac{1}{t}\right)^{t}\right]^{\lim_{x \to +\infty} \frac{3x}{3x-2}} = e^1 = e \]
Risposta finale:
\[ \lim_{x \to +\infty} \left(\frac{6ax+1}{3x-2}\right)^x = \begin{cases} +\infty & \text{se } a > \frac{1}{2} \\ e & \text{se } a = \frac{1}{2} \\ 0^+ & \text{se } 0 < a < \frac{1}{2} \end{cases} \]
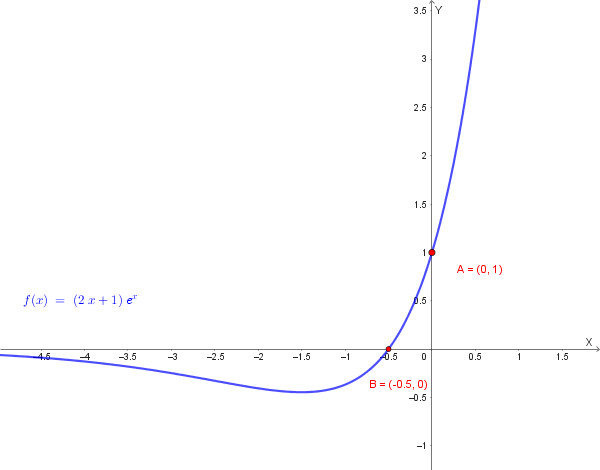
Si consideri la funzione seguente:
\[ y = f(x) = (2x+1) \cdot e^x \]
1. Determinare: Dominio, Intersezioni con gli assi, Parità/Disparità, Segno, Limiti agli estremi del dominio, Asintoti, Eventuali intersezioni con gli asintoti.
2. Indicare la zona del piano in cui si troverà il grafico della funzione.
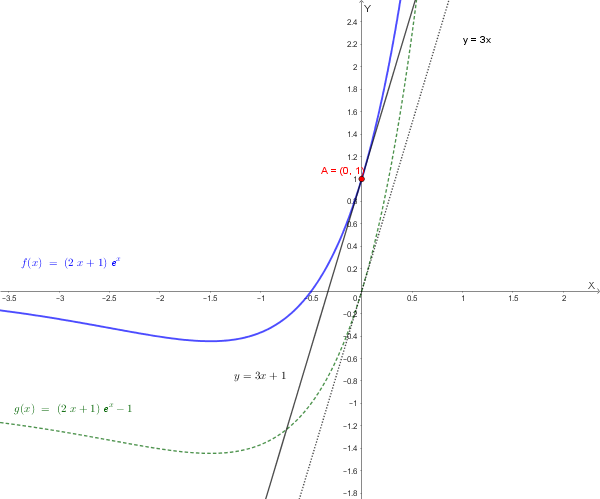
3. Dimostrare che per \(x \to 0\), \(f(x)-1\) è asintotica a \(3x\) e dedurre l'equazione della retta tangente al grafico di \(f\) in \(A=(0,1)\).
4. Tracciare un grafico qualitativo della funzione.
Dominio: La funzione \(f(x) = (2x+1) \cdot e^x\) è definita per ogni \(x \in \mathbb{R}\), quindi il dominio è \(D = \mathbb{R}\).
Intersezioni con gli assi:
Parità/Disparità: Il dominio non è simmetrico rispetto all'origine, quindi la funzione non può essere pari nè dispari. Verifica diretta:
\[ f(-x) = (2(-x)+1) \cdot e^{-x} = (-2x+1) \cdot e^{-x} \neq f(x) \text{ e } \neq -f(x) \]
La funzione non è né pari né dispari.
Segno: Studiamo quando \(f(x) > 0\):
\[ (2x+1) \cdot e^x > 0 \]
Poiché \(e^x > 0\) per ogni \(x\), il segno dipende solo da \(2x+1\):
Limiti agli estremi del dominio:
\[ \lim_{x \to -\infty} (2x+1) \cdot e^x \]
Per \(x \to -\infty\), il termine \((2x+1) \to -\infty\) mentre \(e^x \to 0^+\). Si tratta di una forma indeterminata \((-\infty) \cdot 0\). Riscriviamo il limite come:
\[ \lim_{x \to -\infty} \frac{2x+1}{e^{-x}} \]
Sappiamo che \(e^{-x}\) è un infinito di ordine superiore rispetto a \(x\) per \(x \to -\infty\) (infatti \(e^{-x} \to +\infty\) molto più velocemente di quanto \(2x+1 \to -\infty\)). Quindi il rapporto tende a 0:
\[ \lim_{x \to -\infty} \frac{2x+1}{e^{-x}} = 0^- \]
\[ \lim_{x \to +\infty} (2x+1) \cdot e^x = +\infty \]
Entrambi i fattori tendono a \(+\infty\), quindi anche il prodotto tende a \(+\infty\).
Asintoti:
\[ \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{(2x+1) \cdot e^x}{x} = \lim_{x \to +\infty} \frac{2x+1}{x} \cdot e^x = \lim_{x \to +\infty} \left(2 + \frac{1}{x}\right) \cdot e^x = 2 \cdot (+\infty) = +\infty \]
Poiché il limite è \(+\infty\), non esiste asintoto obliquo per \(x \to +\infty\).
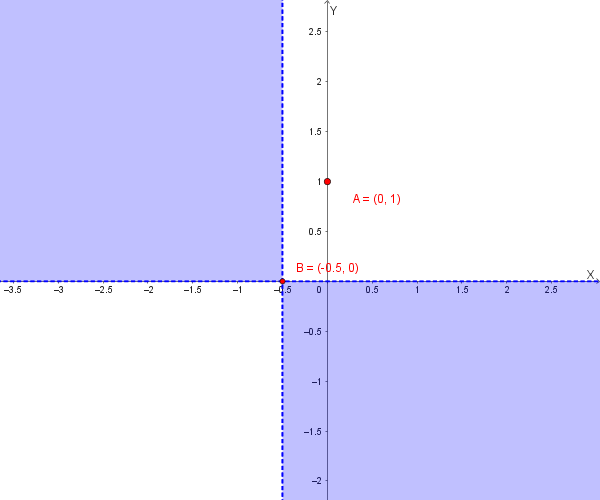
Intersezioni con gli asintoti: L'asintoto è \(y=0\) (asse x). La funzione interseca l'asintoto nel punto \(\left(-\frac{1}{2}, 0\right)\).
Il grafico si trova nelle zone chiare del seguente piano cartesiano:
Dimostriamo che \(f(x) - 1\) è asintotica a \(3x\), cioè:
\[ \lim_{x \to 0} \frac{f(x) - 1}{3x} = 1 \]
Calcoliamo:
\[ \lim_{x \to 0} \frac{(2x+1) \cdot e^x - 1}{3x} \]
Utilizzando il limite notevole \(\displaystyle \lim_{x \to 0} \frac{e^x - 1}{x} = 1\), possiamo scrivere \(e^x \approx 1 + x\) per \(x\) vicino a 0. Quindi:
\[ (2x+1) \cdot e^x \approx (2x+1)(1+x) = 2x + 2x^2 + 1 + x = 1 + 3x + 2x^2 \]
Dunque:
\[ \lim_{x \to 0} \frac{(2x+1) \cdot e^x - 1}{3x} = \lim_{x \to 0} \frac{1 + 3x + 2x^2 - 1}{3x} = \lim_{x \to 0} \frac{3x + 2x^2}{3x} = \lim_{x \to 0} \left(1 + \frac{2x}{3}\right) = 1 \]
Quindi \(f(x) - 1\) è asintotica a \(3x\) per \(x \to 0\).
Retta tangente in \(A=(0,1)\):
Poiché \(f(x)-1\) è asintotica a \(3x\) per \(x \to 0\), la retta tangente nell'origine al grafico di \(f(x)-1\) avrà equazione \(y=3x\).
Il grafico di \(y=f(x)\) si ottiene dal grafico di \(y=f(x)-1\) con una traslazione verticale di vettore \(\vec{v}=(0,1)\).
Quindi la tangente in \(A=(0,1)\) al grafico di \(f(x)\) si ottiene dalla tangente in \(O=(0,0)\) al grafico di \(f(x)-1\) traslandola del vettore \(\vec{v}\).
Perciò l'equazione della retta tangente in \(A\) al grafico di \(f\) è:
\[ y = 3x + 1 \]
Dimostrare che per \(x \to 0^+\):
Dimostrare che \(f(x)=\ln(1+\tan(x))^2\) è asintotica a \(g(x)=e^{2x}-1\) per \(x \to 0^+\)
Due funzioni sono asintotiche se il limite del loro rapporto tende a 1. Calcoliamo:
\[ \lim_{x \to 0^+} \frac{\ln(1+\tan(x))^2}{e^{2x}-1} \]
Semplifichiamo l'espressione al numeratore usando le proprietà dei logaritmi:
\[ \ln(1+\tan(x))^2 = 2\ln(1+\tan(x)) \] (osserviamo che per x \to 0^+ 1+\tan(x)>0
Il limite diventa:
\[ \lim_{x \to 0^+} \frac{2\ln(1+\tan(x))}{e^{2x}-1} \]
Utilizziamo i limiti notevoli. Moltiplichiamo e dividiamo opportunamente:
\[ \lim_{x \to 0^+} \frac{2\ln(1+\tan(x))}{\tan(x)} \cdot \frac{\tan(x)}{x} \cdot \frac{x}{1} \cdot \frac{2x}{e^{2x}-1} \cdot \frac{1}{2x} \]
Riorganizzando:
\[ \lim_{x \to 0^+} 2 \cdot \frac{\ln(1+\tan(x))}{\tan(x)} \cdot \frac{\tan(x)}{x} \cdot \frac{2x}{e^{2x}-1} \cdot \frac{1}{2} \]
Applicando i limiti notevoli:
\[ 2 \cdot 1 \cdot 1 \cdot 1 \cdot \frac{1}{2}= 1 \]
Poiché il limite è uguale 1 le funzioni sono asintotiche.
Dimostrare che \(f(x)=e^{\sin^2(x)}-1\) è infinitesimo di ordine superiore rispetto a \(g(x)=\ln(1+x)+\sin(x)\) per \(x \to 0^+\)
Una funzione \(f(x)\) è infinitesimo di ordine superiore rispetto a \(g(x)\) se:
\[ \lim_{x \to 0^+} \frac{f(x)}{g(x)} = 0 \]
Calcoliamo il limite del rapporto:
\[ \lim_{x \to 0^+} \frac{e^{\sin^2(x)}-1}{\ln(1+x)+\sin(x)} \]
Per il numeratore, utilizziamo il limite notevole \(\displaystyle \lim_{x \to 0} \frac{e^x-1}{x} = 1\):
\[ e^{\sin^2(x)}-1 \sim \sin^2(x) \text{ per } x \to 0 \]
Per il denominatore, utilizziamo i limiti notevoli:
\[ \ln(1+x) \sim x \text{ e } \sin(x) \sim x \text{ per } x \to 0 \]
Quindi:
\[ \ln(1+x)+\sin(x) \sim x + x = 2x \text{ per } x \to 0^+ \]
Il limite diventa:
\[ \lim_{x \to 0^+} \frac{\sin^2(x)}{2x} = \lim_{x \to 0^+} \frac{\sin^2(x)}{x^2} \cdot \frac{x^2}{2x} = 1 \cdot \lim_{x \to 0^+} \frac{x}{2} = 0 \]
Poiché il limite è 0, \(f(x)\) è effettivamente infinitesimo di ordine superiore rispetto a \(g(x)\).
Parte principale e ordine di infinitesimo
Per \(f(x)=(1-\cos(x)) \cdot \ln(\sqrt{1+x})\):
Utilizziamo i limiti notevoli per \(x \to 0\):
Quindi:
\[ f(x) \sim \frac{x^2}{2} \cdot \frac{x}{2} = \frac{x^3}{4} \]
Parte principale: \(\displaystyle \frac{x^3}{4}\)
Ordine di infinitesimo: 3
Per \(g(x)=x \cdot \sin^2(x)\):
Utilizziamo il limite notevole \(\sin(x) \sim x\) per \(x \to 0\):
\[ g(x) = x \cdot \sin^2(x) \sim x \cdot x^2 = x^3 \]
Parte principale: \(x^3\)
Ordine di infinitesimo: 3
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.