



Questo compito è stato assegnato nel mese di Ottobre 1988 a una classe 5ª del Liceo Scientifico.
Argomenti: Dimostrazione monotonia con definizione, grafico di funzione deducibile, simmetrica di una funzione rispetto ad una retta, equazioni simmetria assiale,
funzione inversa, grafico di una funzione inversa, funzione composta, funzione omografica e grafici deducibili con traformazioni geometriche,
calcolo di limiti.
Si consideri la seguente funzione: \(y=f(x)=\sqrt{1-x}\).
Punto 1) Dimostrare, servendosi della definizione, che la funzione è monotòna.
La funzione è \(y=f(x)=\sqrt{1-x}\). Per il dominio, deve essere \(1-x \ge 0\), quindi \(x \le 1\). Il dominio è \((-\infty, 1]\).
Dimostrariamo che la funzione è monotòna decrescente, verificando che che per ogni \(x_1, x_2\) nel dominio, se \(x_1 < x_2\), allora \(f(x_1)> f(x_2)\).
Consideriamo \(x_1 < x_2 \le 1\). Abbiamo:
Quindi, \(f(x_1) > f(x_2)\). Questo dimostra che la funzione è **monotòna strettamente decrescente** nel suo dominio.
Punto 2) Tracciare il grafico della funzione.
Il grafico della funzione \(y=f(x)\) si ottiene dal grafico di \(a(x)=\sqrt{x}\) mediante le seguenti trasformazioni geometriche:
Il grafico della funzione \(y=f(x)\) è mostrato nella seguente figura:
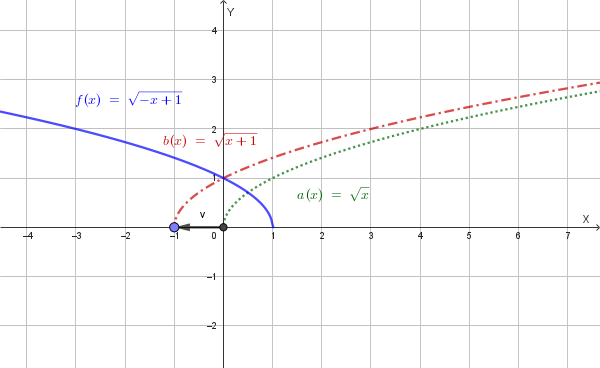
Punto 3) Scrivere l'equazione della simmetrica della funzione f rispetto alla retta y=2.
Per trovare la simmetrica di una funzione \(y=f(x)\) rispetto a una retta orizzontale \(y=k\), usiamo la formula: \(y' = 2k - y\). Nel nostro caso, \(k=2\) e \(y=f(x)=\sqrt{1-x}\). Sostituendo, otteniamo la funzione simmetrica \(g(x)\):
\(y' = 2(2) - \sqrt{1-x} = 4 - \sqrt{1-x}\)
L'equazione della funzione simmetrica è \(g(x) = 4 - \sqrt{1-x}\).
Il grafico della simmetrica di f rispetto alla retta y=2 è quindi il seguente:
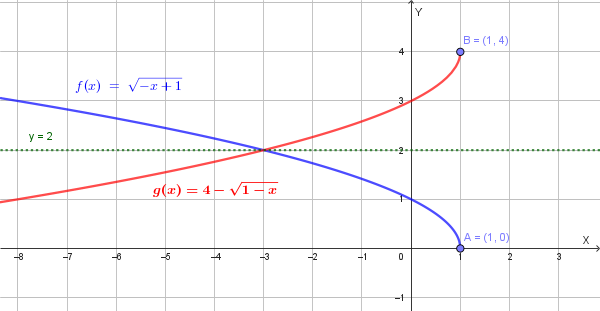
Punto 4) Dire perché la funzione f è invertibile e scrivere l'equazione della funzione inversa g(x).
La funzione \(f(x)=\sqrt{1-x}\) è invertibile perché è **strettamente monotòna** (abbiamo dimostrato al punto 1 che è strettamente decrescente).
Per trovare la funzione inversa, seguiamo questi passaggi:
La funzione inversa è \(g(x) = 1-x^2\). Per quanto riguarda il dominio della funzione inversa, esso corrisponde al codominio della funzione di partenza. La funzione \(f(x)\) ha come codominio \([0, +\infty)\). Di conseguenza, la funzione inversa \(g(x)\) è definita per \(x \ge 0\).
Punto 5) Tracciare il grafico della funzione y=g(x) deducendolo da quello di y=f(x).
Il grafico della funzione inversa \(y=g(x)\) si ottiene facendo una **simmetria assiale** del grafico di \(y=f(x)\) rispetto alla retta \(y=x\).
Il grafico di \(y=g(x)\) è quindi il seguente:
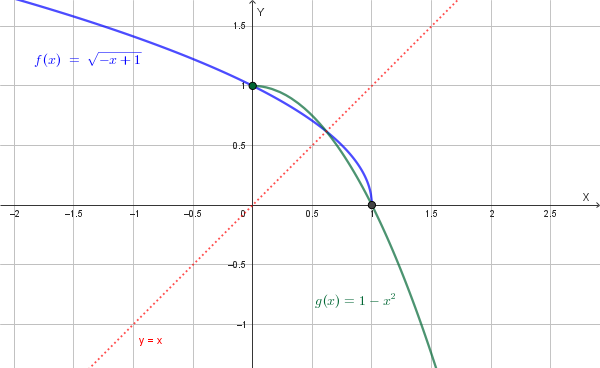
Date le funzioni \(f(x)=\frac{1}{\sqrt{1-x}}\) e \(g(x)=\ln(x)\):
Date le funzioni \(f(x)=\frac{1}{\sqrt{1-x}}\) e \(g(x)=\ln(x)\).
Prima di iniziare, è utile determinare i domini delle due funzioni di partenza:
Punto 1) Trovare l'equazione della funzione composta \(f \circ g\) e indicare il suo dominio.
La funzione composta \(f \circ g\) si ottiene sostituendo \(x\) con \(g(x)\) nella funzione \(f(x)\):
\((f \circ g)(x) = f(g(x)) = \frac{1}{\sqrt{1-g(x)}} = \frac{1}{\sqrt{1-\ln(x)}}\)
Per il dominio della funzione composta, dobbiamo considerare due condizioni:
Risolviamo la seconda condizione:
\(1 > \ln(x) \implies \ln(x) < 1\)
Poiché il logaritmo naturale ha base \(e\), possiamo scrivere:
\(e^{\ln(x)} < e^1 \implies x < e\)
Combinando le due condizioni (\(x > 0\) e \(x < e\)), il dominio della funzione composta \(f \circ g\) è \((0, e)\).
Punto 2) Trovare l'equazione della funzione composta \(g \circ f\) e indicare il suo dominio.
La funzione composta \(g \circ f\) si ottiene sostituendo \(x\) con \(f(x)\) nella funzione \(g(x)\):
\((g \circ f)(x) = g(f(x)) = \ln(f(x)) = \ln\left(\frac{1}{\sqrt{1-x}}\right)\)
Per il dominio della funzione composta, dobbiamo considerare due condizioni:
La condizione \(\frac{1}{\sqrt{1-x}} > 0\) è sempre verificata all'interno del dominio di \(f(x)\), poiché la radice quadrata di un numero positivo è sempre positiva e il numeratore è 1.
Pertanto, il dominio della funzione composta \(g \circ f\) è semplicemente il dominio della funzione interna, ovvero \((-\infty, 1)\).
Punto 3) Qual è il dominio della funzione \(f(x) \cdot g(x)\)?
La funzione prodotto è definita come \(y = f(x) \cdot g(x) = \frac{1}{\sqrt{1-x}} \cdot \ln(x)\). Il dominio di un prodotto di funzioni è l'**intersezione** dei domini delle singole funzioni.
Dominio di \(f(x)\): \((-\infty, 1)\)
Dominio di \(g(x)\): \((0, +\infty)\)
L'intersezione dei due domini è l'insieme di tutti i numeri che appartengono a entrambi i domini. Graficamente, possiamo immaginarli su una linea numerica:
Dominio di f(x): <--------------------------------)
-∞ 1
Dominio di g(x): (-------------------------->
0 +∞
Intersezione: (--------------------)
0 1
L'intersezione è l'intervallo \((0, 1)\).
Il dominio della funzione prodotto \(f(x) \cdot g(x)\) è \((0, 1)\).
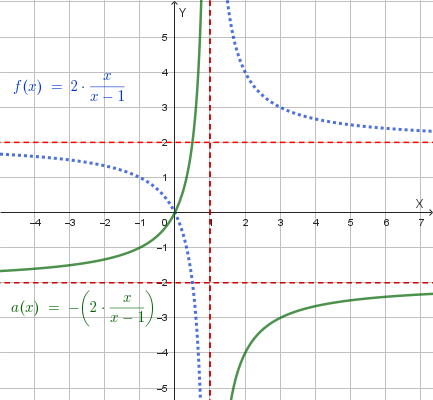
Data la funzione \(y=f(x)=\frac{ax+b}{cx+d}\) dimostrare che quella che soddisfa le seguenti condizioni:
ha equazione \(f(x)=\frac{2x}{x-1}\).
Rappresentare poi le seguenti funzioni:
Per dimostrare l'equazione della funzione \(f(x)\) data, analizziamo le tre condizioni.
Sostituendo \(a=2c\) e \(b=0\) nell'equazione della funzione iniziale, otteniamo \(f(x) = \frac{2cx}{cx-c} = \frac{2x}{x-1}\).
Il grafico della funzione \(f(x)=\frac{2x}{x-1}\) è il seguente:
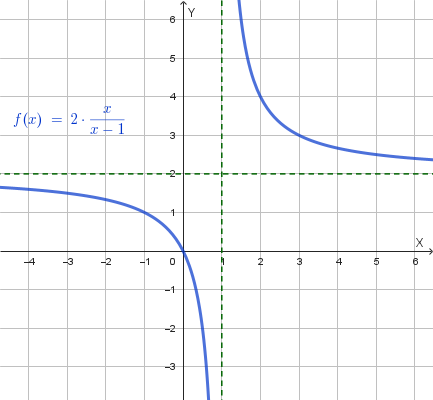
Grafici delle funzioni trasformate:
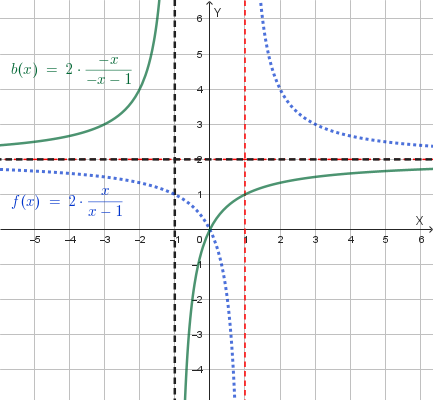
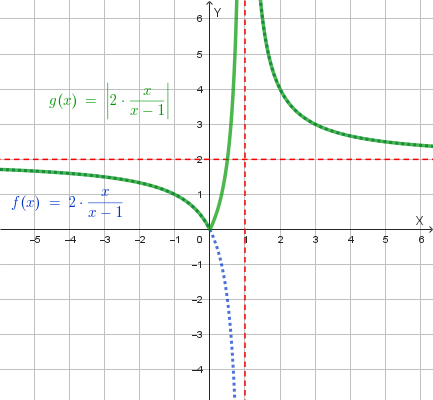
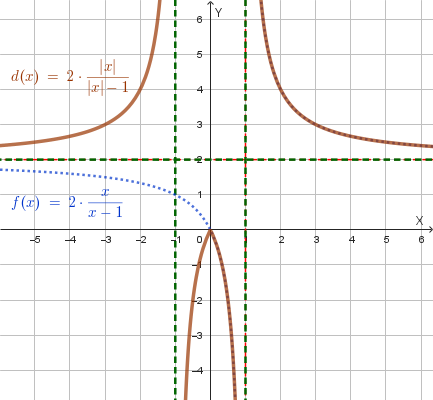
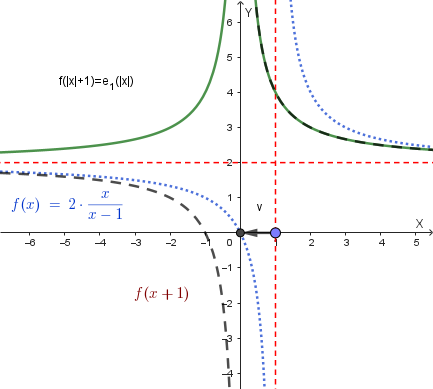
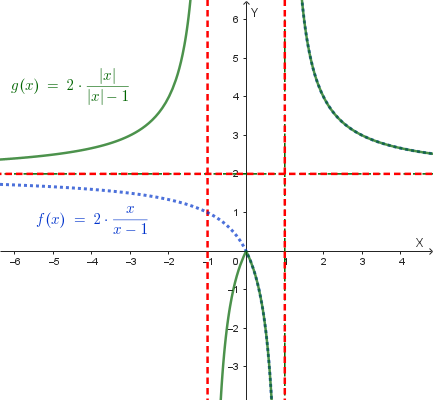
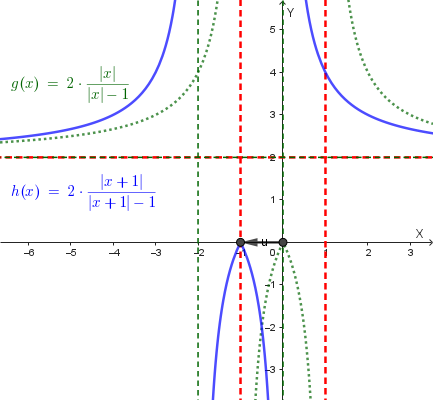
Successivamente, si applica una **traslazione a sinistra di 1 unità** del grafico di \(f(|x|)\) per ottenere il grafico finale di \(y=f(|x+1|)\). Il grafico finale è:
Calcolare i seguenti limiti:
\(\lim_{x \to 0} \frac{e^{2x}-1}{\sin(3x)}\)
Il limite si presenta nella forma indeterminata \( \frac{0}{0} \). Per risolverlo, usiamo i **limiti notevoli** moltiplicando e dividendo per gli argomenti delle funzioni esponenziali e trigonometriche:
\[ \lim_{x \to 0} \frac{e^{2x}-1}{\sin(3x)} = \lim_{x \to 0} \frac{e^{2x}-1}{2x} \cdot \frac{2x}{1} \cdot \frac{1}{\sin(3x)} \]
Ora manipoliamo l'espressione per far comparire i limiti notevoli:
\[ \lim_{x \to 0} \left( \frac{e^{2x}-1}{2x} \right) \cdot \left( \frac{3x}{\sin(3x)} \right)^{-1} \cdot \frac{2x}{3x} = 1 \cdot 1^{-1} \cdot \frac{2}{3} = \frac{2}{3} \]
Il risultato è \( \frac{2}{3} \).
\(\lim_{x \to +\infty} \sin(x) \cdot \ln(1+\frac{1}{x})\)
In questo limite, consideriamo i due fattori separatamente:
Per il **teorema del confronto**, il prodotto di una funzione **limitata** e una funzione che tende a **zero** è sempre uguale a zero.
\[ \lim_{x \to +\infty} \sin(x) \cdot \ln(1+\frac{1}{x}) = 0 \]
\(\lim_{x \to 0} \frac{\ln(\cos(x))}{\sin^2(x)}\)
Il limite è della forma \( \frac{0}{0} \). Per risolverlo, applichiamo un trucco al numeratore e usiamo i limiti notevoli. Aggiungiamo e sottraiamo 1 all'argomento del logaritmo:
\[ \lim_{x \to 0} \frac{\ln(1+(\cos(x)-1))}{\sin^2(x)} \]
Ora usiamo il limite notevole del logaritmo, moltiplicando e dividendo per l'argomento \( \cos(x)-1 \):
Ricordiamo che il limite notevole è: \( \lim_{f(x) \to 0} \frac{\ln(1+f(x))}{f(x)} = 1 \)
\[ \lim_{x \to 0} \frac{\ln(1+(\cos(x)-1))}{\cos(x)-1} \cdot \frac{\cos(x)-1}{\sin^2(x)} \]
Il primo termine tende a 1. Semplifichiamo il secondo termine. Ricordando che \( \cos(x)-1 = - (1-\cos(x)) \) e che \( \sin^2(x) = 1 - \cos^2(x) = (1-\cos(x))(1+\cos(x)) \):
\[ \lim_{x \to 0} 1 \cdot \frac{-(1-\cos(x))}{(1-\cos(x))(1+\cos(x))} = \lim_{x \to 0} \frac{-1}{1+\cos(x)} = \frac{-1}{1+\cos(0)} = \frac{-1}{1+1} = -\frac{1}{2} \]
Il risultato è \( -\frac{1}{2} \).
\(\lim_{x \to +\infty} (3x) \cdot (2^{\frac{1}{x}}-1)\)
Il limite è della forma \( \infty \cdot 0 \). Effettuiamo una sostituzione: poniamo \(y = \frac{1}{x}\). Quando \(x \to +\infty\), allora \(y \to 0\). Il limite diventa:
\[ \lim_{y \to 0} 3\frac{1}{y} \cdot (2^y-1) = \lim_{y \to 0} 3 \cdot \frac{2^y-1}{y} \]
Questa è la forma del limite notevole \( \lim_{x \to 0} \frac{a^x - 1}{x} = \ln(a) \). Quindi:
\[ 3 \cdot \lim_{y \to 0} \frac{2^y-1}{y} = 3 \cdot \ln(2) \]
Il risultato è \( 3 \ln(2) \).
\(\lim_{x \to 0} \frac{\sqrt{1-x}-1}{\tan(\frac{x}{2})}\)
Il limite è della forma \( \frac{0}{0} \). Per risolverlo, useremo due limiti notevoli: quello del binomio e quello della tangente.
Per il numeratore, applichiamo il limite notevole \( \lim_{x \to 0} \frac{(1+x)^k - 1}{x} = k \). L'espressione si può scrivere come \( (1-x)^{\frac{1}{2}}-1 \). Sostituendo \(-x\) con \(x\) e \(k = \frac{1}{2}\):
\[ \frac{\sqrt{1-x}-1}{-x} \to \frac{1}{2} \]
Per il denominatore, applichiamo il limite notevole \( \lim_{x \to 0} \frac{\tan(x)}{x} = 1 \), ponendo \(x\) come \( \frac{x}{2} \):
\[ \frac{\tan(\frac{x}{2})}{\frac{x}{2}} \to 1 \]
Tornando al limite iniziale, manipoliamo l'espressione per far comparire i limiti notevoli:
\[ \lim_{x \to 0} \frac{\sqrt{1-x}-1}{\tan(\frac{x}{2})} = \lim_{x \to 0} \frac{\sqrt{1-x}-1}{-x} \cdot (-x) \cdot \frac{1}{\tan(\frac{x}{2})} \]
\[ = \lim_{x \to 0} \left( \frac{\sqrt{1-x}-1}{-x} \right) \cdot \left( \frac{\frac{x}{2}}{\tan(\frac{x}{2})} \right)^{-1} \cdot \frac{-x}{\frac{x}{2}} \]
\[ = \frac{1}{2} \cdot 1^{-1} \cdot \frac{-1}{\frac{1}{2}} = \frac{1}{2} \cdot (-2) = -1 \]
Il risultato è \( -1 \).
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.