



Questo compito è stato assegnato nel mese di Ottobre 1986 a una classe 5ª del Liceo Scientifico.
Argomenti: funzione composta, grafici deducibili, funzione inversa, grafico di una funzione, tangente in un punto del grafico di una funzione.
Si considerino le funzioni \(f(x)=\frac{1}{\sqrt{2-x}}\) e \(g(x)=2\ln(x)\).
a) Scrivere l'equazione della funzione composta \(F=f\circ g\) e trovare il suo dominio.
b) Scrivere l'equazione della funzione composta \(G=g\circ f\) e trovare il suo dominio.
c) Trovare il dominio della funzione \(f(x)+g(x)\).
d) Calcolare il limite per \(x \to 2^-\) di \(f(x)\cdot g(x)\).
La funzione composta \(F=f\circ g\) si ottiene sostituendo \(g(x)\) al posto di \(x\) nella funzione \(f(x)\).
Quindi \(F(x) = f(g(x)) = f(2\ln(x)) = \frac{1}{\sqrt{2-2\ln(x)}}\).
Per il dominio, dobbiamo porre il denominatore strettamente maggiore di zero:
\(2-2\ln(x)>0 \implies 2 > 2\ln(x) \implies 1 > \ln(x) \implies e^1 > x\).
Inoltre, il dominio della funzione "interna" \(g(x)\) è \(x>0\).
Il dominio di \(F(x)\) è l'intersezione di queste due condizioni: \(x>0 \text{ e } x<e\).
Pertanto, il dominio è \((0, e)\).
La funzione composta \(G=g\circ f\) si ottiene sostituendo \(f(x)\) al posto di \(x\) nella funzione \(g(x)\).
Quindi \(G(x) = g(f(x)) = g\left(\frac{1}{\sqrt{2-x}}\right) = 2\ln\left(\frac{1}{\sqrt{2-x}}\right)\).
Per il dominio, dobbiamo porre l'argomento del logaritmo strettamente maggiore di zero:
\(\frac{1}{\sqrt{2-x}}>0\). Poiché il numeratore è sempre positivo, dobbiamo solo assicurarci che il denominatore sia definito e positivo, cioè \(2-x>0 \implies x<2\).
Inoltre, dobbiamo considerare il dominio della funzione "interna" \(f(x)\), che è \(2-x>0 \implies x<2\).
Il dominio di \(G(x)\) è \(x<2\), cioè \((-\infty, 2)\).
La somma delle funzioni \(f(x)+g(x)\) è data da \(f(x)+g(x) = \frac{1}{\sqrt{2-x}} + 2\ln(x)\).
Il dominio di questa funzione è l'intersezione dei domini di \(f(x)\) e \(g(x)\).
Dominio di \(f(x)\): \(2-x>0 \implies x<2\).
Dominio di \(g(x)\): \(x>0\).
L'intersezione dei due domini è \(x>0 \text{ e } x<2\), quindi il dominio è \((0, 2)\).
Dobbiamo calcolare il limite per \(x \to 2^-\) di \(f(x)\cdot g(x)\).
\(f(x)\cdot g(x) = \frac{1}{\sqrt{2-x}}\cdot 2\ln(x)\).
Calcoliamo i limiti separati:
\[ \lim_{x \to 2^-} \frac{1}{\sqrt{2-x}} = \frac{1}{\sqrt{2-2^-}} = \frac{1}{\sqrt{0^+}} = \frac{1}{0^+} = +\infty \]
\[ \lim_{x \to 2^-} 2\ln(x) = 2\ln(2) \]
Il limite del prodotto è il prodotto dei limiti: \(+\infty \cdot 2\ln(2) = +\infty\).
Data la funzione di equazione \(y=f(x)=\arcsin(2x-1)\):
1. determinare il suo dominio.
2. rappresentare graficamente la funzione \(y=f(x)\), deducendola da una funzione elementare e indicando le trasformazioni geometriche utilizzate.
3. Dimostrare che la funzione \(y=f(x)\) è invertibile utilizzando il suo grafico.
4. Trovare l'equazione della funzione inversa di \(f(x)\), indicandola con \(y=g(x)\) e rappresentarla graficamente sfruttando il legame che c'è fra il grafico di una funzione e quello della sua inversa.
La funzione data è \(y=f(x)=\arcsin(2x-1)\). Il dominio della funzione arcoseno è definito per valori compresi tra -1 e 1. Dobbiamo quindi risolvere la seguente disequazione:
\[ -1 \le 2x-1 \le 1 \]
Aggiungiamo 1 a tutti i membri della disequazione per isolare il termine con la \(x\):
\[ -1+1 \le 2x-1+1 \le 1+1 \]
\[ 0 \le 2x \le 2 \]
Dividiamo tutti i membri per 2:
\[ \frac{0}{2} \le \frac{2x}{2} \le \frac{2}{2} \]
\[ 0 \le x \le 1 \]
Il dominio della funzione è l'intervallo chiuso \([0, 1]\).
Il grafico di \(y=f(x)\) si ottiene dal grafico della funzione elementare \(y=\arcsin(x)\) con i seguenti passaggi:
- \(a(x)=\arcsin(x)\)
- \(b(x)= \arcsin(x-1)\): traslazione di vettore \(\vec{v}=(1,0)\), cioè verso destra di 1.
- \(f(x)=b(2x)=\arcsin(2x-1)\): contrazione orizzontale di fattore 2.
Quindi il grafico di \(f(x)\) è il seguente:
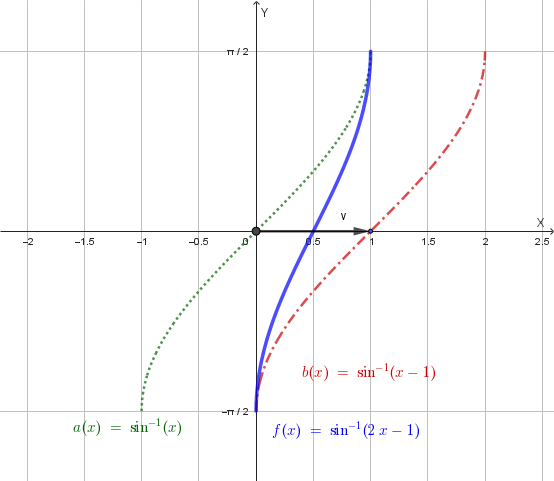
Il grafico della funzione \(f(x)=\arcsin(2x-1)\) mostra che è una funzione monotona strettamente crescente sul suo dominio \([0, 1]\). Poiché è sempre crescente, ogni retta orizzontale interseca il suo grafico in un solo punto. Questa proprietà è nota come Criterio della retta orizzontale e garantisce che la funzione sia invertibile.
Per trovare l'equazione della funzione inversa \(g(x)\), partiamo dall'equazione \(y=\arcsin(2x-1)\). Scambiamo le variabili \(x\) e \(y\):
\[ x = \arcsin(2y-1) \]
Ora, risolviamo rispetto a \(y\). Applichiamo la funzione seno ad entrambi i membri:
\[ \sin(x) = 2y-1 \]
Aggiungiamo 1 ad entrambi i membri:
\[ \sin(x)+1 = 2y \]
Dividiamo per 2 per isolare \(y\):
\[ y = \frac{\sin(x)+1}{2} \]
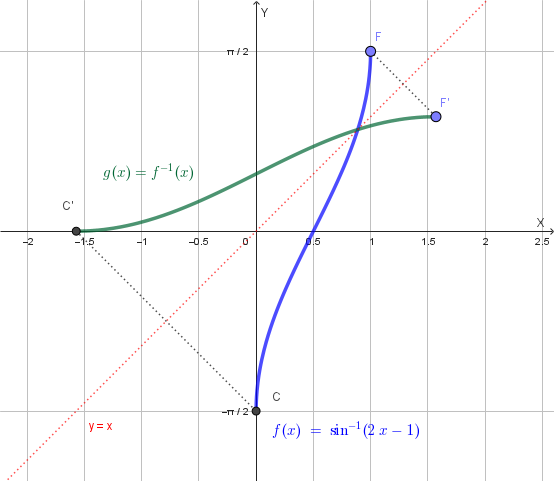
Quindi l'equazione della funzione inversa è \(g(x) = \frac{\sin(x)+1}{2}\). Il dominio di \(g(x)\) corrisponde al codominio (o range) di \(f(x)\), che è \( [-\frac{\pi}{2}, \frac{\pi}{2}] \).
Il grafico di \(g(x)\) si ottiene da quello di \(f(x)\) mediante una simmetria rispetto alla retta \(y=x\).
Data la funzione \(f(x)=\sqrt{4-3x}\):
1. dimostrare, servendosi della definizione, che è monotòna.
2. tracciare il suo grafico deducendolo dal grafico di \(y=\sqrt{x}\), indicando le trasformazioni geometriche utilizzate.
3. scrivere l'equazione della simmetrica di \(f(x)\) rispetto all'asse y.
4. dedurre dal grafico di \(f(x)\) il grafico di \(f(\frac{x}{3}+1)\).
5. considerata la trasformazione \(T\) di equazioni: \(X=x-1\), \(Y=2y-4\), scrivere l'equazione della corrispondente di \(f(x)\) nella \(T\) e rappresentarla graficamente.
Il dominio della funzione \(f(x)=\sqrt{4-3x}\) è definito per \(4-3x \ge 0\), da cui \(x \le \frac{4}{3}\). Per verificare se la funzione è monotona, consideriamo due valori \(x_1\) e \(x_2\) nel dominio, tali che \(x_1 < x_2\). Moltiplicando per -3, si ottiene \(-3x_1 > -3x_2\). Aggiungendo 4, si ha \(4-3x_1 > 4-3x_2\). Poiché la funzione radice quadrata è strettamente crescente, si ha \(\sqrt{4-3x_1} > \sqrt{4-3x_2}\), ovvero \(f(x_1) > f(x_2)\). Questo dimostra che la funzione è strettamente decrescente.
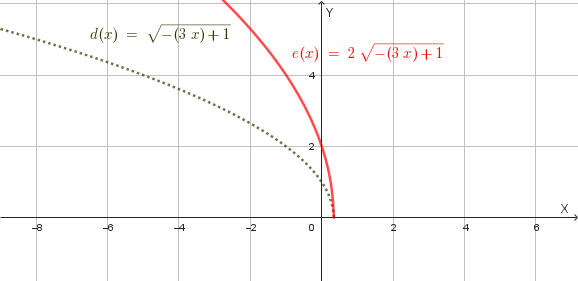
La funzione \(f(x)=\sqrt{4-3x}\) si può ottenere dal grafico della funzione elementare \(a(x)=\sqrt{x}\) mediante le seguenti trasformazioni geometriche:
Il grafico della funzione \(f(x)\) è quindi il seguente:
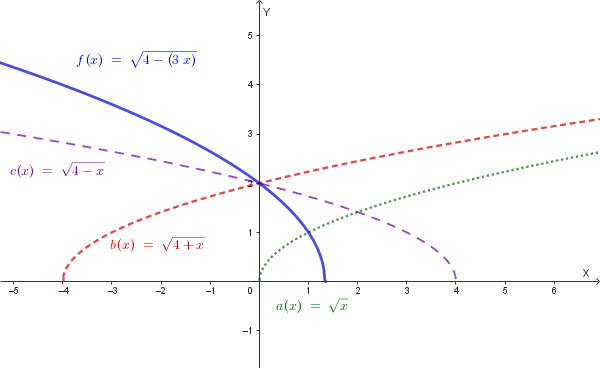
Per trovare la funzione simmetrica rispetto all'asse y, è sufficiente sostituire \(x\) con \(-x\) nell'equazione di \(f(x)\). L'equazione della funzione simmetrica è \(y = \sqrt{4-3(-x)} = \sqrt{4+3x}\).
Il suo grafico è il seguente:
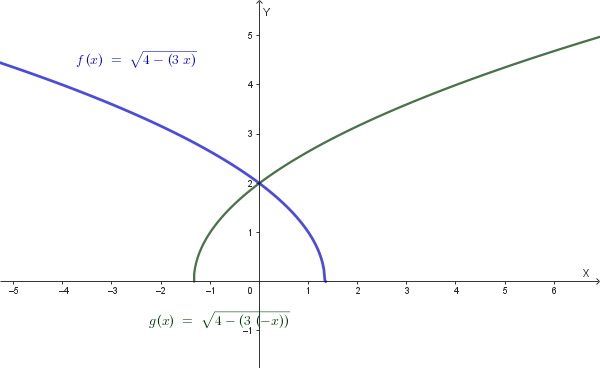
Il grafico di \(f(\frac{x}{3}+1)\) si ottiene dal grafico di \(f(x)\) mediante le seguenti trasformazioni:
Sostituendo \(\frac{x}{3}+1\) a \(x\) nella funzione \(f(x)\), si ottiene \(f(\frac{x}{3}+1) = \sqrt{4-3(\frac{x}{3}+1)} = \sqrt{4-x-3} = \sqrt{1-x}\).
Il grafico di \(g(x) = \sqrt{1-x}\) è il seguente:
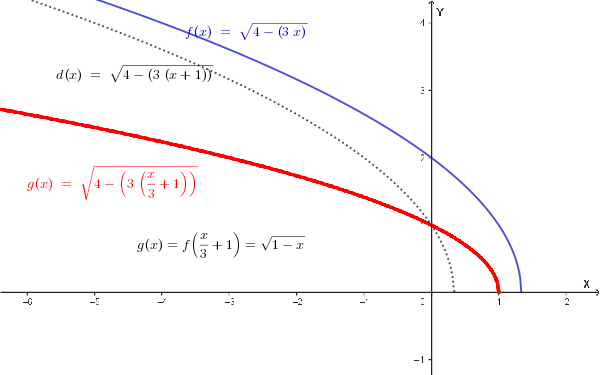
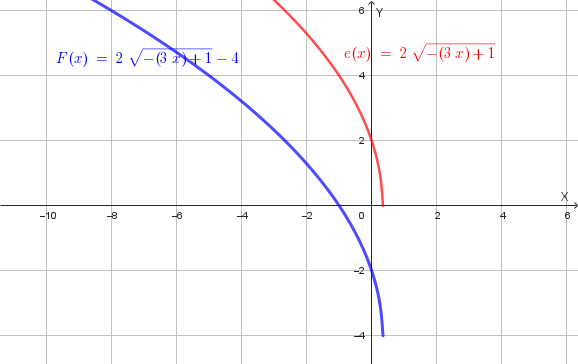
Per trovare l'equazione della trasformata di \(f(x)\) nella trasformazione \(T\), che ha equazioni \(X=x-1\) e \(Y=2y-4\), dobbiamo esprimere \(x\) e \(y\) in funzione di \(X\) e \(Y\): \(x=X+1\) e \(y=\frac{Y+4}{2}\). Sostituiamo queste espressioni nell'equazione di \(f(x)\):
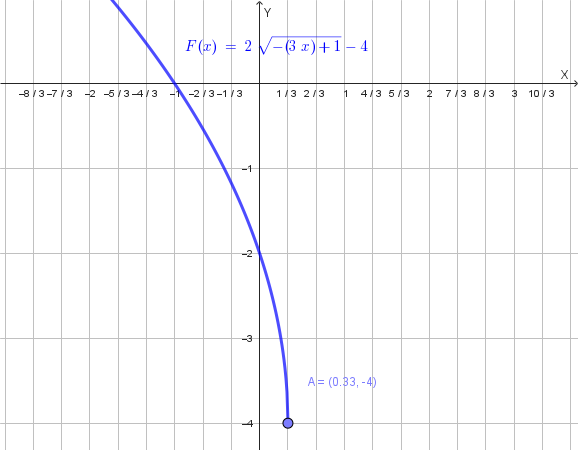
\[ \frac{Y+4}{2} = \sqrt{4-3(X+1)} \] \[ Y+4 = 2\sqrt{4-3X-3} \] \[ Y = 2\sqrt{1-3X}-4 \]L'equazione della funzione corrispondente è \(Y=2\sqrt{1-3X}-4\). Il suo grafico si ottiene applicando le seguenti trasformazioni geometriche, partendo dalla funzione elementare \(a(x)=\sqrt{x}\):
Il grafico finale è il seguente:
È data la funzione di equazione \(y=f(x)=\frac{x^2-3x+2}{x^2-1}\):
1. Si studi la funzione e la si rappresenti graficamente.
2. Verificato che la funzione ha un asintoto orizzontale e uno verticale, si consideri il punto \(A\) della funzione di ascissa \(-3\) e si determini l'equazione della tangente \(t\) al grafico della funzione nel punto \(A\).
3. Detti \(B\) e \(C\) le intersezioni di tale tangente con gli asintoti orizzontale e verticale, e indicato con \(D\) il punto di intersezione degli asintoti, si calcoli l'area del triangolo \(BCD\).
4. Dimostrare che, al variare di \(A\) sul grafico di \(f\), l'area del triangolo \(BCD\) rimane costante.
La funzione data è \(y=f(x)=\frac{x^2-3x+2}{x^2-1}\). Per studiarla, semplifichiamo l'espressione fattorizzando numeratore e denominatore:
Il numeratore può essere scomposto in \((x-1)(x-2)\), mentre il denominatore, essendo una differenza di quadrati, si scompone in \((x-1)(x+1)\). La funzione diventa quindi: \[ y = \frac{(x-1)(x-2)}{(x-1)(x+1)} \]
Possiamo semplificare il termine \((x-1)\), a patto di specificare che la funzione originale non è definita per \(x=1\). Otteniamo l'equazione di una **funzione omografica**: \[ y = \frac{x-2}{x+1} \]
Il dominio della funzione è \(D = \mathbb{R} \setminus \{-1, 1\}\). La funzione ha un'asintoto verticale e uno orizzontale. Il punto in cui la funzione non è definita (\(x=1\)) è un "buco" nel grafico.
Il centro dell'iperbole è l'intersezione degli asintoti, ovvero \(D(-1, 1)\). Il grafico della funzione \(y=f(x)\) è il seguente:
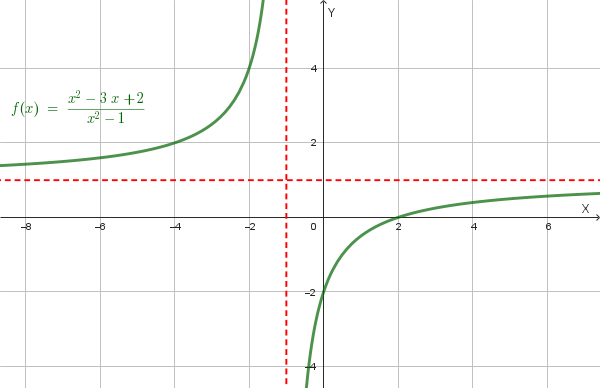
Consideriamo il punto \(A\) di ascissa \(x_A=-3\). La sua ordinata è \(y_A = f(-3) = \frac{-3-2}{-3+1} = \frac{-5}{-2}=\frac{5}{2}\). Il punto è \(A(-3, \frac{5}{2})\).
Per trovare l'equazione della retta tangente, consideriamo una retta generica passante per \(A\): \[ y - y_A = m(x-x_A) \implies y-\frac{5}{2}=m(x+3) \]
Mettiamo a sistema questa equazione con quella dell'iperbole e poniamo la condizione che l'intersezione sia un solo punto. Per fare ciò, il discriminante dell'equazione risolvente deve essere nullo (\(\Delta = 0\)).
Sostituiamo l'espressione di \(y\) della retta nell'equazione dell'iperbole: \[ m(x+3)+\frac{5}{2} = \frac{x-2}{x+1} \]
Moltiplichiamo entrambi i membri per \((x+1)\) e riordiniamo i termini in un'equazione di secondo grado in \(x\): \[ (x+1)\left(m(x+3)+\frac{5}{2}\right) = x-2 \]
\[ (x+1)\left(mx+3m+\frac{5}{2}\right) = x-2 \] \[ mx^2+3mx+\frac{5}{2}x+mx+3m+\frac{5}{2} = x-2 \] \[ mx^2 + \left(4m+\frac{5}{2}-1\right)x + \left(3m+\frac{5}{2}+2\right) = 0 \] \[ mx^2 + \left(4m+\frac{3}{2}\right)x + \left(3m+\frac{9}{2}\right) = 0 \]Ora, poniamo il discriminante \(\Delta = b^2-4ac\) uguale a zero per trovare il valore di \(m\): \[ \Delta = \left(4m+\frac{3}{2}\right)^2 - 4m\left(3m+\frac{9}{2}\right) = 0 \]
\[ 16m^2+2\cdot4m\cdot\frac{3}{2}+\frac{9}{4} - 12m^2-18m=0 \] \[ 16m^2+12m+\frac{9}{4}-12m^2-18m=0 \] \[ 4m^2-6m+\frac{9}{4}=0 \]Moltiplicando per 4 per eliminare la frazione: \[ 16m^2-24m+9=0 \] Questa è un quadrato perfetto, \((4m-3)^2=0\), da cui \(4m-3=0 \implies m=\frac{3}{4}\).
Sostituiamo il valore di \(m\) nell'equazione della retta per trovare l'equazione della tangente \(t\): \[ y-\frac{5}{2}=\frac{3}{4}(x+3) \implies y=\frac{3}{4}x+\frac{9}{4}+\frac{5}{2} \implies y=\frac{3}{4}x+\frac{19}{4} \]
Il grafico della funzione e della tangente è il seguente:
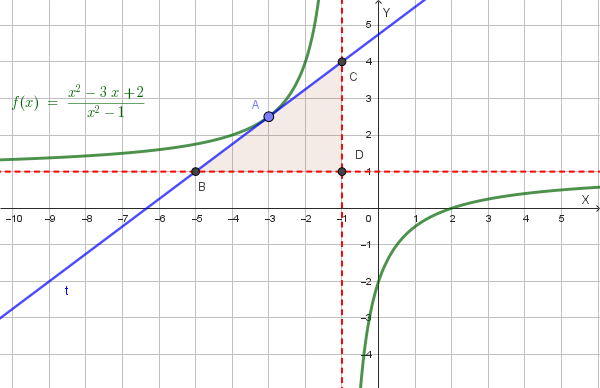
I vertici del triangolo sono le intersezioni della tangente \(t\) con gli asintoti (\(B\) e \(C\)) e il punto di intersezione degli asintoti \(D(-1, 1)\).
Il triangolo \(BCD\) è un triangolo rettangolo con i cateti paralleli agli assi cartesiani. La lunghezza della base è la distanza tra \(B\) e \(D\): \(b = |x_D-x_B| = |-1-(-5)| = 4\). La lunghezza dell'altezza è la distanza tra \(C\) e \(D\): \(h = |y_C-y_D| = |4-1| = 3\).
L'area del triangolo è: \[ \text{Area}_{BCD} = \frac{1}{2} \cdot \text{base} \cdot \text{altezza} = \frac{1}{2} \cdot 4 \cdot 3 = 6 \]
Per dimostrare che l'area non dipende dal punto scelto, consideriamo un punto generico \(A(x_0, f(x_0))\) sull'iperbole. Usando lo stesso metodo del discriminante nullo, si può dimostrare che il coefficiente angolare della tangente in un punto generico \(A\) è \(m=\frac{3}{(x_0+1)^2}\).
Per trovare il coefficiente angolare \(m\), impostiamo l'equazione della retta generica passante per il punto \(A\) e la mettiamo a sistema con l'equazione dell'iperbole. La condizione di tangenza richiede che l'equazione risolvente abbia un'unica soluzione, che si ottiene ponendo il suo discriminante uguale a zero (\(\Delta = 0\)).
La retta generica passante per \(A(x_0, \frac{x_0-2}{x_0+1})\) è: \[ y = m(x-x_0) + \frac{x_0-2}{x_0+1} \]
Uguagliando questa equazione a quella dell'iperbole \(y = \frac{x-2}{x+1}\), otteniamo l'equazione risolvente: \[ m(x-x_0) + \frac{x_0-2}{x_0+1} = \frac{x-2}{x+1} \]
Per semplificare, portiamo i termini con la frazione su un lato e risolviamo l'espressione: \[ m(x-x_0) = \frac{x-2}{x+1} - \frac{x_0-2}{x_0+1} = \frac{(x-2)(x_0+1) - (x_0-2)(x+1)}{(x+1)(x_0+1)} \]
Espandendo e semplificando il numeratore, si ottiene: \[ (xx_0+x-2x_0-2) - (xx_0+x_0-2x-2) = 3x - 3x_0 = 3(x-x_0) \]
Sostituendo il risultato nell'equazione precedente: \[ m(x-x_0) = \frac{3(x-x_0)}{(x+1)(x_0+1)} \]
Questa equazione può essere riscritta come: \[ (x-x_0)\left[ m - \frac{3}{(x+1)(x_0+1)} \right] = 0 \]
Affinché la retta sia tangente all'iperbole, l'unica soluzione possibile deve essere \(x=x_0\). Questo si verifica quando l'espressione nella parentesi quadra si annulla esattamente in \(x=x_0\): \[ m - \frac{3}{(x_0+1)(x_0+1)} = 0 \implies m = \frac{3}{(x_0+1)^2} \]
Questo dimostra che il valore del coefficiente angolare è \(m=\frac{3}{(x_0+1)^2}\).
L'equazione della tangente in \(A\) è \(y-f(x_0)=m(x-x_0)\). Sostituendo le espressioni generali, otteniamo:
Calcoliamo l'area del triangolo \(BCD\) con vertici \(B(2x_0+1, 1)\), \(C(-1, \frac{x_0-5}{x_0+1})\) e \(D(-1, 1)\):
\[ \text{Area}_{BCD} = \frac{1}{2} \cdot |x_D-x_B| \cdot |y_C-y_D| = \frac{1}{2} \cdot |-1-(2x_0+1)| \cdot |\frac{x_0-5}{x_0+1}-1| \] \[ \text{Area}_{BCD} = \frac{1}{2} \cdot |-2(x_0+1)| \cdot |\frac{-6}{x_0+1}| = \frac{1}{2} \cdot 2|x_0+1| \cdot \frac{6}{|x_0+1|} = 6 \]Poiché il risultato è un numero fisso (6) e non dipende da \(x_0\), l'area del triangolo rimane sempre **costante**, indipendentemente dal punto \(A\) scelto sulla funzione.
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.