



Questo compito è stato assegnato il giorno 09 Ottobre 1990 a una classe 5ª del Liceo Scientifico.
Argomenti: Trasformazioni geometriche, Parabola, Dimostrazione della monotonia di una funzione, Funzione inversa, Grafico della funzione inversa, Simmetrica di una funzione rispetto ad un punto, Proprietà degli insiemi di numeri reali (estremo inferiore e superiore, massimo e minimo di un insieme, punti di accumulazione, punti interni, punti esterni, punti di frontiera), Funzione composta.
\[ \begin{cases} X=2x-2 \\ Y=(1/2)y+1 \end{cases} \]
la si rappresenti graficamente.L'equazione generale di una parabola con asse di simmetria verticale è \(y = ax^2 + bx + c\). Per trovare i coefficienti \(a, b, c\), sostituiamo le coordinate dei tre punti A, B e C nell'equazione:
\[ \begin{cases} 0 = a(-1)^2 + b(-1) + c \quad \text{(passaggio per A)} \\ 0 = a(3)^2 + b(3) + c \quad \text{(passaggio per B)} \\ 3 = a(0)^2 + b(0) + c \quad \text{(passaggio per C)} \end{cases} \]
Dalla terza equazione, otteniamo immediatamente \(c=3\). Sostituiamo questo valore nelle prime due equazioni:
\[ \begin{cases} a - b + 3 = 0 \\ 9a + 3b + 3 = 0 \end{cases} \]
Dalla prima equazione ricaviamo \(b = a+3\). Sostituiamo nella seconda:
\[ 9a + 3(a+3) + 3 = 0 \\ 9a + 3a + 9 + 3 = 0 \\ 12a = -12 \implies a = -1 \]
Ora troviamo \(b\):
\[ b = a+3 = -1+3 = 2 \]
I coefficienti sono \(a=-1\), \(b=2\), \(c=3\). L'equazione della parabola \(p\) è quindi:
\[ y = -x^2 + 2x + 3 \]
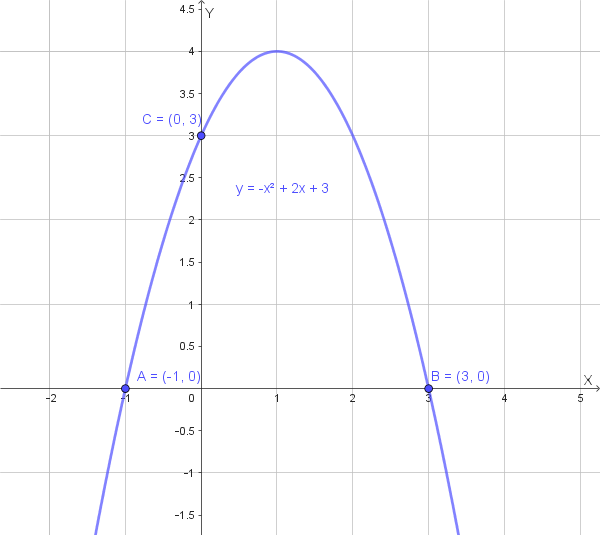
Si tratta di una parabola con asse parallelo all'asse y, passante per i punti dati A, B e C, con vertice V=(1; 4).
Il suo grafico è il seguente:
Le equazioni della trasformazione sono: \( \begin{cases} X=2x-2 \\ Y=(1/2)y+1 \end{cases} \). Per trovare l'equazione di \(p'\), dobbiamo esprimere \(x\) e \(y\) in funzione di \(X\) e \(Y\):
\[ \begin{cases} 2x = X+2 \implies x = \frac{1}{2}X+1 \\ \frac{1}{2}y = Y-1 \implies y = 2Y-2 \end{cases} \]
Sostituiamo queste espressioni nell'equazione della parabola \(p\), \(y = -x^2 + 2x + 3\):
\[ 2Y-2 = -\left(\frac{1}{2}X+1\right)^2 + 2\left(\frac{1}{2}X+1\right) + 3 \]
Sviluppiamo e semplifichiamo:
\[ 2Y-2 = -\left(\frac{1}{4}X^2 + X + 1\right) + X+2+3 \\ 2Y-2 = -\frac{1}{4}X^2 - X - 1 + X+5 \\ 2Y-2 = -\frac{1}{4}X^2 + 4 \\ 2Y = -\frac{1}{4}X^2 + 6 \\ Y = -\frac{1}{8}X^2 + 3 \]
L'equazione della parabola trasformata \(p'\) è \(y = -\frac{1}{8}x^2 + 3\).
Il vertice di \(p\) è \(V = (-\frac{2}{2(-1)}; -\frac{2^2-4(-1)(3)}{4(-1)}) = (1; 4)\). Il vertice di \(p'\) è \(V'=(0; 3)\).
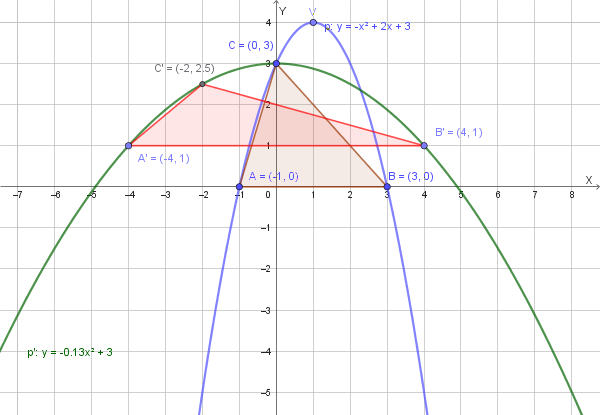
Calcoliamo le coordinate dei punti trasformati A', B' e C' usando le equazioni di T: \( \begin{cases} X=2x-2 \\ Y=(1/2)y+1 \end{cases} \).
Calcoliamo l'area del triangolo ABC. La base AB si trova sull'asse delle ascisse e ha lunghezza \(|3 - (-1)| = 4\). L'altezza relativa a questa base è l'ordinata del punto C, cioè 3. L'area è:
\[ \text{Area}(ABC) = \frac{1}{2} \cdot \text{base} \cdot \text{altezza} = \frac{1}{2} \cdot 4 \cdot 3 = 6 \]
Calcoliamo l'area del triangolo A'B'C'. La base A'B' si trova sulla retta \(y=1\) e ha lunghezza \(|4 - (-4)| = 8\). L'altezza relativa a questa base è la differenza tra l'ordinata di C' e l'ordinata della base, cioè \(2.5 - 1 = 1.5\). L'area è:
\[ \text{Area}(A'B'C') = \frac{1}{2} \cdot \text{base} \cdot \text{altezza} = \frac{1}{2} \cdot 8 \cdot 1.5 = 4 \cdot 1.5 = 6 \]
Poiché le due aree sono uguali, i triangoli sono equivalenti.
La trasformazione \(T\) data è un'**affinità generica**, in quanto le sue equazioni sono del tipo:
\[ \begin{cases} X=ax+by+c \\ Y=a'x+b'y+c' \end{cases} \]
Nel nostro caso, le equazioni sono: \( \begin{cases} X=2x+0y-2 \\ Y=0x+\frac{1}{2}y+1 \end{cases} \).
La matrice dei coefficienti lineari è: \[ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ 0 & \frac{1}{2} \end{pmatrix} \]
Il determinante di questa matrice è: \( \det = (2) \cdot (\frac{1}{2}) - (0) \cdot (0) = 1 \). Poiché il determinante è diverso da zero, la trasformazione è non degenere.
Il **rapporto di affinità**, che corrisponde al rapporto tra le aree di due figure corrispondenti, è uguale alla radice quadrata del valore assoluto del determinante della matrice. Quindi:
\[ \text{Rapporto di affinità} = \sqrt{|\det|} = \sqrt{|1|} = 1 \]
Questo rapporto pari a 1 significa che le figure corrispondenti hanno la stessa area, confermando che i triangoli ABC e A'B'C' sono equivalenti, come già dimostrato nel punto c).
Punti uniti: I punti uniti sono quelli che coincidono con la loro immagine. Dobbiamo risolvere il sistema di equazioni ponendo \(X=x\) e \(Y=y\):
\[ \begin{cases} x = 2x-2 \\ y = \frac{1}{2}y+1 \end{cases} \]
Risolvendo la prima equazione:
\[ x = 2x-2 \implies -x = -2 \implies x=2 \]
Risolvendo la seconda equazione:
\[ y = \frac{1}{2}y+1 \implies \frac{1}{2}y = 1 \implies y=2 \]
Esiste un unico punto unito, di coordinate \((2; 2)\).
Rette unite: Una retta \(y=mx+q\) è unita se la sua immagine è la retta stessa. Sostituiamo \(x = \frac{1}{2}X+1\) e \(y = 2Y-2\) nell'equazione della retta:
\[ 2Y-2 = m\left(\frac{1}{2}X+1\right) + q \\ 2Y-2 = \frac{m}{2}X+m+q \\ 2Y = \frac{m}{2}X+m+q+2 \\ Y = \frac{m}{4}X + \frac{m+q+2}{2} \]
Questa retta deve coincidere con \(Y=mX+q\). Uguagliamo i coefficienti:
\[ \begin{cases} m = \frac{m}{4} \quad \text{(coefficiente angolare)} \\ q = \frac{m+q+2}{2} \quad \text{(intercetta)} \end{cases} \]
Dalla prima equazione: \(m = \frac{m}{4} \implies 4m=m \implies 3m=0 \implies m=0\). L'unica retta unita non verticale deve avere pendenza nulla.
Sostituiamo \(m=0\) nella seconda equazione:
\[ q = \frac{0+q+2}{2} \implies 2q=q+2 \implies q=2 \]
L'unica retta unita (non verticale) è \(y=0x+2\), ovvero la retta orizzontale \(y=2\).
Verifichiamo anche l'esistenza di rette verticali unite, della forma \(x=k\). Sostituiamo \(x = \frac{1}{2}X+1\):
\[ \frac{1}{2}X+1 = k \implies X = 2k-2 \]
Affinché la retta sia unita, dobbiamo avere \(X=k\). Quindi \(k = 2k-2 \implies -k=-2 \implies k=2\). Esiste una retta unita verticale, la retta \(x=2\).
Le rette unite sono \(y=2\) e \(x=2\). Si incrociano nel punto unito \((2;2)\).
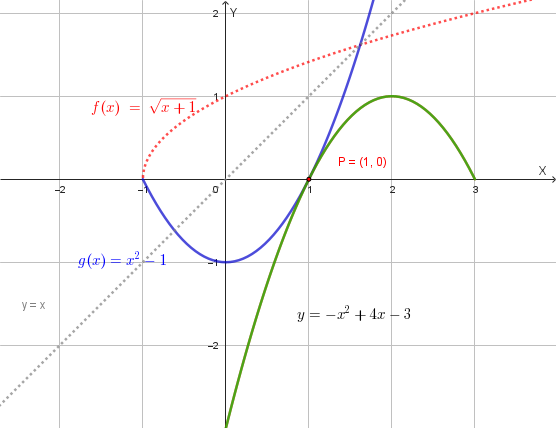
Dimostrare, servendosi della definizione, che la funzione di equazione \(y=f(x)=\sqrt{x+1}\) è monotona; dedurre che è invertibile e, detta \(g(x)\) la funzione inversa, rappresentare quest'ultima insieme alla sua simmetrica rispetto al punto \(P=(1; 0)\).
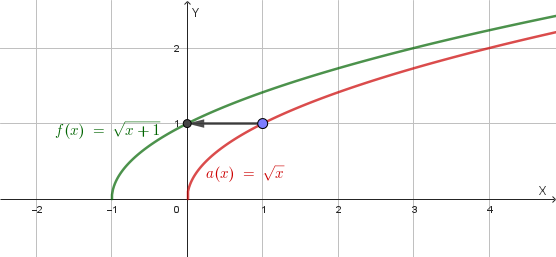
La funzione data è \(f(x)=\sqrt{x+1}\). Il suo dominio è \(x+1 \ge 0 \implies x \ge -1\). L'immagine della funzione è \(y \ge 0\).
Il suo grafico si ottiene da \(y=\sqrt{x}\) con una traslazione orizzontale di vettore \(\vec{v}=(-1; 0)\). Il suo grafico è il seguente:
Per dimostrare che la funzione è monotona, usiamo la definizione. Consideriamo due valori qualsiasi \(x_1\) e \(x_2\) nel dominio della funzione, tali che \(x_1 < x_2\). Dobbiamo dimostrare che \(f(x_1) < f(x_2)\).
Partiamo dalla disuguaglianza \(x_1 < x_2\). Sommiamo 1 a entrambi i membri:
\[ x_1+1 < x_2+1 \]Dato che la radice quadrata è una funzione crescente per valori non negativi, possiamo applicarla a entrambi i membri mantenendo il verso della disuguaglianza:
\[ \sqrt{x_1+1} < \sqrt{x_2+1} \]Questo equivale a \(f(x_1) < f(x_2)\). Poiché abbiamo dimostrato che per ogni \(x_1 < x_2\) si ha \(f(x_1) < f(x_2)\), la funzione è strettamente crescente e quindi monotona.
Poiché la funzione \(f(x)\) è strettamente monotona, è anche iniettiva e quindi invertibile. Per trovare l'equazione della funzione inversa, scambiamo le variabili \(x\) e \(y\) e risolviamo l'equazione per la nuova \(y\):
\[ y = \sqrt{x+1} \]
\[ x = \sqrt{y+1} \]
Eleviamo al quadrato entrambi i membri (ricordando che \(x \ge 0\)):
\[ x^2 = y+1 \]
Isoliamo \(y\):
\[ y = x^2-1 \]
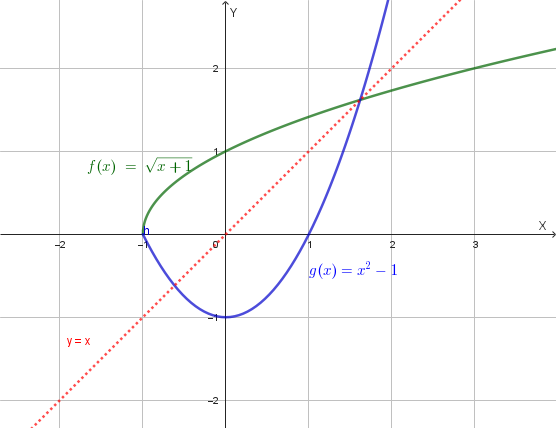
La funzione inversa è \(g(x) = x^2-1\). Il dominio di \(g(x)\) è l'immagine di \(f(x)\), cioè \(x \ge 0\). L'immagine di \(g(x)\) è il dominio di \(f(x)\), cioè \(y \ge -1\).
Grafico di \(g(x)\) insieme a quello di \(f(x)\):
La trasformazione di simmetria rispetto a un punto \(P=(x_P, y_P)\) ha equazioni:
\[ \begin{cases} x' = 2x_P - x \\ y' = 2y_P - y \end{cases} \]
Nel nostro caso, \(P=(1; 0)\), quindi le equazioni sono:
\[ \begin{cases} x' = 2(1) - x \implies x = 2 - x' \\ y' = 2(0) - y \implies y = -y' \end{cases} \]
Sostituiamo queste espressioni nell'equazione di \(g(x)\), che è \(y = x^2-1\):
\[ -y' = (2-x')^2 - 1 \]
Sviluppiamo e risolviamo per \(y'\):
\[ -y' = (4 - 4x' + (x')^2) - 1 \\ -y' = (x')^2 - 4x' + 3 \\ y' = -(x')^2 + 4x' - 3 \]
La funzione simmetrica di \(g(x)\) rispetto a \(P\) è \(h(x) = -x^2+4x-3\).
Di seguito sono rappresentati i grafici delle tre funzioni: \(f(x)=\sqrt{x+1}\) (in rosso), la sua inversa \(g(x)=x^2-1\) (in blu) e la simmetrica di \(g(x)\) rispetto a \(P=(1,0)\) (in verde). La retta \(y=x\) è tracciata in grigio per evidenziare la simmetria tra \(f(x)\) e \(g(x)\).
Dato l'insieme \( E=\left\{x \in \mathbb{R} \mid x=\frac{n^{2}-3 n+2}{n^{2}-1}, \quad n=2,3, \ldots\right\} \), determinare:
Dimostrare che, detto \( a_n \) il generico punto di \( E \), risulta \( a_n < a_{n+1} \) per ogni \( n=2,3, \ldots \).
Il termine generico della successione è \( a_n = \frac{n^2-3n+2}{n^2-1} \). Possiamo semplificare questa espressione scomponendo il numeratore e il denominatore.
Sostituendo queste scomposizioni, otteniamo:
\[ a_n = \frac{(n-1)(n-2)}{(n-1)(n+1)} \]Poiché il dominio della successione è \( n \ge 2 \), \( n-1 \ne 0 \) e possiamo semplificare il termine \( (n-1) \):
\[ a_n = \frac{n-2}{n+1} \]Questa è la forma semplificata del termine generico.
Dobbiamo dimostrare che \( a_n < a_{n+1} \) per ogni \( n=2, 3, \ldots \). Confrontiamo \( a_n \) e \( a_{n+1} \):
\[ a_n = \frac{n-2}{n+1} \] \[ a_{n+1} = \frac{(n+1)-2}{(n+1)+1} = \frac{n-1}{n+2} \]Dobbiamo verificare se \( \frac{n-2}{n+1} < \frac{n-1}{n+2} \). Moltiplichiamo entrambi i membri per \( (n+1)(n+2) \), che è un valore positivo per \( n \ge 2 \), quindi il verso della disuguaglianza non cambia:
\[ (n-2)(n+2) < (n-1)(n+1) \]Usiamo i prodotti notevoli:
\[ n^2-4 < n^2-1 \]Sottraiamo \( n^2 \) da entrambi i membri:
\[ -4 < -1 \]Questa disuguaglianza è vera. Pertanto, la successione \( a_n \) è **strettamente crescente** per \( n \ge 2 \).
Poiché la successione è strettamente crescente, l'estremo inferiore dell'insieme è il suo primo termine. Per l'estremo superiore, osserviamo il comportamento della successione calcolando i primi termini:
I valori sembrano crescere e avvicinarsi a 1. Facciamo l'ipotesi che l'estremo superiore sia 1 e dimostriamolo usando la definizione.
I valori di \( a_n \) possono essere visti come le ordinate dei punti della funzione \( f(x)=\frac{x-2}{x+1} \), che è un'iperbole equilatera traslata, quando la \( x \) assume i valori naturali \( x=2, x=3, x=4, \text{ etc.} \).
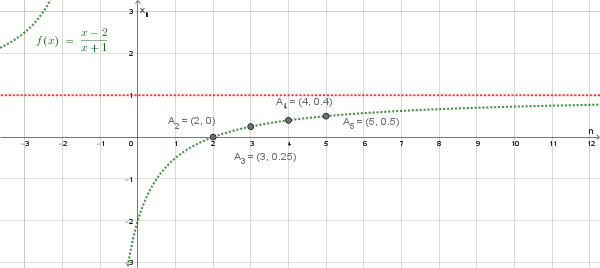
**1. Estremo inferiore (inf) e minimo:** Il valore più piccolo dell'insieme è il primo termine della successione, cioè \( a_2 = 0 \). Quindi, \( \inf E = 0 \). Poiché \( 0 \in E \), **il minimo esiste ed è 0**.
**2. Estremo superiore (sup) e massimo:** Per dimostrare che \( \sup E = 1 \), dobbiamo verificare due condizioni:
\[ \frac{n-2}{n+1} \le 1 \]
Moltiplichiamo entrambi i membri per \( n+1 \), che è un valore positivo:
\[ n-2 \le n+1 \implies -2 \le 1 \]
Questa disuguaglianza è sempre vera, quindi 1 è un maggiorante per l'insieme \( E \).
\[ \frac{n-2}{n+1} > 1-\epsilon \]
Risolviamo questa disuguaglianza per \( n \):
\[ n-2 > (1-\epsilon)(n+1) = n+1-\epsilon n - \epsilon \]
Riorganizziamo i termini per isolare \( n \):
\[ \epsilon n > 1+2-\epsilon = 3 - \epsilon; n > \frac{3-\epsilon}{\epsilon} = \frac{3}{\epsilon}-1 \]
Poiché per ogni \( \epsilon > 0 \) possiamo sempre trovare un numero naturale \( n \) (sufficientemente grande) che soddisfi questa condizione, la seconda condizione è verificata. Quindi, **l'estremo superiore è 1**. Poiché nessun elemento della successione raggiunge il valore 1 (altrimenti avremmo \( n-2 = n+1 \), che è impossibile), **il massimo non esiste**.
**3. Punti di accumulazione:** L'unico punto di accumulazione è il valore a cui la successione si avvicina, ovvero **il punto 1**. Tutti gli altri punti dell'insieme sono isolati.
**4. Punti isolati:** Tutti i punti di \( E \) sono punti isolati.
**5. Punti interni ed esterni e frontiera:** Nessun punto di \( E \) è interno. **L'insieme dei punti interni è vuoto**. La frontiera di \( E \) è l'insieme stesso, unito al suo punto di accumulazione, cioè \( E \cup \{1\} \).
Sono date le funzioni di equazioni:
Determinare le equazioni delle funzioni composte \(F(x)=f(g(x))\) e \(G(x)= g(f(x))\) e rappresentarle graficamente.
Per calcolare la funzione composta \(F(x)=f(g(x))\) dobbiamo analizzare la funzione \(g(x)\) e sostituirla nei rami della funzione \(f(x)\).
In questo caso, \(g(x)=2x\). Dobbiamo capire se il risultato di \(g(x)\) rientra nel primo o nel secondo ramo di \(f(x)\). Dato che \(x \le 0\), la funzione \(g(x)=2x\) avrà sempre un valore \(g(x) \le 0\). Questo significa che dobbiamo usare il primo ramo di \(f(x)\), cioè \(f(x)=x+1\).
Sostituiamo \(g(x)\) al posto di \(x\):
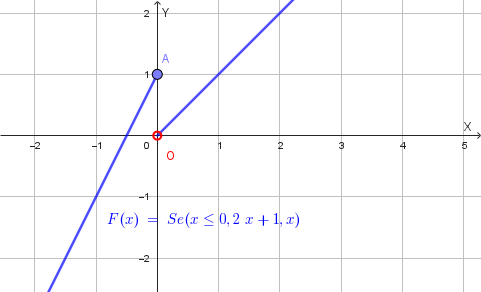
\[F(x) = f(g(x)) = g(x)+1 = 2x+1\]Quindi, per \(x \le 0\), la funzione composta è \(F(x)=2x+1\).
In questo caso, \(g(x)=e^x\). Dobbiamo capire se il risultato di \(g(x)\) rientra nel primo o nel secondo ramo di \(f(x)\). Dato che \(x > 0\), la funzione \(g(x)=e^x\) avrà sempre un valore \(g(x) > 1\). Questo significa che dobbiamo usare il secondo ramo di \(f(x)\), cioè \(f(x)=\ln(x)\).
Sostituiamo \(g(x)\) al posto di \(x\):
\[F(x) = f(g(x)) = \ln(g(x)) = \ln(e^x)\]Ricordando che \(\ln(e^x)=x\), la funzione composta è semplicemente:
\[F(x) = x\]Quindi, per \(x > 0\), la funzione composta è \(F(x)=x\).
Unendo i due casi, l'equazione della funzione composta \(F(x)\) è:
\[F(x)= \begin{cases} 2x+1 & \text{se } x \le 0 \\ x & \text{se } x > 0 \end{cases}\]Questo è il grafico di F(x):
Per calcolare la funzione composta \(G(x)=g(f(x))\) dobbiamo analizzare la funzione \(f(x)\) e sostituirla nei rami della funzione \(g(x)\).
In questo caso, \(f(x)=x+1\). Dobbiamo capire se il risultato di \(f(x)\) rientra nel primo o nel secondo ramo di \(g(x)\).
Il valore di \(f(x)\) è \(x+1\). Se \(x \le 0\), allora \(x+1 \le 1\).
Dobbiamo considerare due sottocasi per il valore di \(x+1\):
Se \(x+1 > 0\), cioè \(x > -1\). In questo caso, il valore di \(f(x)\) è positivo, quindi usiamo il primo ramo di \(g(x)\), cioè \(g(x)=e^x\). Dobbiamo ricordarci che questo vale solo per \(x\) compreso tra \(-1\) e \(0\).
Sostituiamo \(f(x)\) al posto di \(x\):
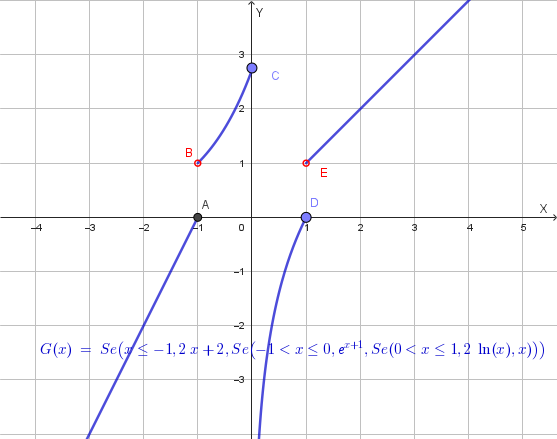
\[G(x) = g(f(x)) = e^{f(x)} = e^{x+1}\]Se \(x+1 \le 0\), cioè \(x \le -1\). In questo caso, il valore di \(f(x)\) è negativo o nullo, quindi usiamo il secondo ramo di \(g(x)\), cioè \(g(x)=2x\).
Sostituiamo \(f(x)\) al posto di \(x\):
\[G(x) = g(f(x)) = 2f(x) = 2(x+1) = 2x+2\]In questo caso, \(f(x)=\ln(x)\). Dato che \(x > 0\), la funzione \(\ln(x)\) può assumere valori sia positivi che negativi. Anche qui, dobbiamo considerare due sottocasi:
Se \(\ln(x) > 0\), cioè \(x > 1\). In questo caso, il valore di \(f(x)\) è positivo, quindi usiamo il primo ramo di \(g(x)\), cioè \(g(x)=e^x\).
Sostituiamo \(f(x)\) al posto di \(x\):
\[G(x) = g(f(x)) = e^{f(x)} = e^{\ln(x)}\]Ricordando che \(e^{\ln(x)}=x\), la funzione composta è semplicemente:
\[G(x) = x\]Se \(\ln(x) \le 0\), cioè \(0 < x \le 1\). In questo caso, il valore di \(f(x)\) è negativo o nullo, quindi usiamo il secondo ramo di \(g(x)\), cioè \(g(x)=2x\).
Sostituiamo \(f(x)\) al posto di \(x\):
\[G(x) = g(f(x)) = 2f(x) = 2\ln(x)\]Unendo tutti i casi, l'equazione della funzione composta \(G(x)\) è:
\[G(x)= \begin{cases} 2x+2 & \text{se } x \le -1 \\ e^{x+1} & \text{se } -1 < x \le 0 \\ 2\ln(x) & \text{se } 0 < x \le 1 \\ x & \text{se } x > 1 \end{cases}\]Questo il grafico di G(x):
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.