



Questo compito è stato assegnato il giorno 18 Dicembre 1990 a una classe 5ª del Liceo Scientifico.
Argomenti: Problema con parabola che conduce ad una funzione, Studio di una funzione razionale fratta, Simmetrica di una funzione rispetto all'asse x e rispetto all'origine degli assi, Area regione delimitata da due parabole,
Area regione delimitata da una parabola e da una retta, Segmento parabolico.
In un sistema di riferimento cartesiano ortogonale \(Oxy\) è data la parabola \(p\) di equazione:
\[ y = \frac{1}{4}x^2 - 1. \]
Detto \(P\) il generico punto della parabola, \(H\) la sua proiezione sull’asse \(x\) e \(V\) il vertice della parabola stessa, trova — in funzione dell’ascissa \(x\) di \(P\) — la funzione di equazione:
\[ y = f(x) = \frac{16\,\overline{PV}^2}{\overline{OH}^3 - \overline{OV}}. \]
Individua le coordinate di \(H\) in corrispondenza delle quali la funzione non esiste.
1️⃣ Studio della parabola:
La parabola ha equazione \( y = \frac{1}{4}x^2 - 1 \).
Il grafico della parabola, insieme ai segmenti richiesti ( \(PV\), \(OH\), \(OV\)), è il seguente:
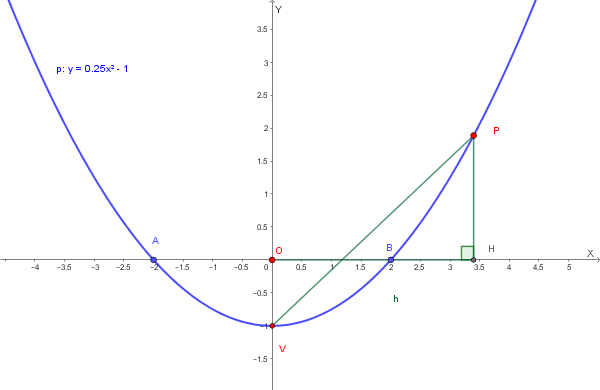
2️⃣ Coordinate dei punti:
3️⃣ Misure dei segmenti:
4️⃣ Costruzione della funzione:
Sostituendo i valori nella relazione data:
\[ y = f(x) = \frac{16\,\overline{PV}^2}{\overline{OH}^3 - \overline{OV}} = \frac{16\,x^2\left(1 + \frac{x^2}{16}\right)}{|x|^3 - 1}. \]
Semplificando si ottiene:
\[ f(x) = \frac{x^4 + 16x^2}{|x|^3 - 1}. \]
5️⃣ Dominio e punti di non esistenza:
La funzione non è definita per i valori di \(x\) tali che il denominatore \(|x|^3 - 1 = 0\), cioè per:
\[ |x| = 1 \Rightarrow x = \pm 1. \]
D(f) = ℝ \ {−1, 1}
Conclusione:
Nell'Esercizio 1 si è ottenuta la funzione
\[ f(x)=\frac{x^4+16x^2}{|x|^3-1}. \]
Studiare qualitativamente la funzione
\[ g(x)=\frac{x^4+16x^2}{x^3-1}, \]
determinando: dominio, intersezioni con gli assi, parità/disparità, segno, limiti alla frontiera del dominio, eventuali asintoti ed eventuali intersezioni con gli asintoti.
1️⃣ Dominio
La funzione è definita per tutti i reali per i quali il denominatore è diverso da zero:
\[ x^3-1 \neq 0 \Longrightarrow x \neq 1. \]
D(g)=\mathbb{R}\setminus\{1\}.
2️⃣ Intersezioni con gli assi
3️⃣ Parità / disparità
Calcoliamo \(g(-x)\):
\[ g(-x)=\frac{(-x)^4+16(-x)^2}{(-x)^3-1}=\frac{x^4+16x^2}{-x^3-1} \neq g(x),\quad g(-x)\neq -g(x). \]
Quindi la funzione non è né pari né dispari.
4️⃣ Segno della funzione
Il numeratore \(x^4+16x^2\) è sempre non negativo e si annulla solo per \(x=0\). Il segno di \(g(x)\) è quindi determinato dal segno del denominatore \(x^3-1\):
5️⃣ Limiti alle frontiere del dominio
\[ g(x) = \frac{x^4+16x^2}{x^3-1} \approx \frac{x^4}{x^3} = x. \]
Per \(x \to +\infty\), il termine dominante è positivo, quindi
\[ \lim_{x \to +\infty} g(x) = +\infty. \]
Per \(x \to -\infty\), il termine dominante è negativo, quindi
\[ \lim_{x \to -\infty} g(x) = -\infty. \]
Non esistono quindi asintoti orizzontali, mentre possono esistere asintoti obliqui (dato che il grado del numeratore supera di 1 il grado del denominatore possiamo dire che ci saranno asintoti obliqui).
6️⃣ Asintoti (calcolo dettagliato dell'asintoto obliquo)
Per trovare un eventuale asintoto obliquo della forma \(y=mx+q\) si usa la regola dei limiti:
Calcolo di \(m\)
\[ \frac{g(x)}{x}=\frac{1}{x}\cdot\frac{x^4+16x^2}{x^3-1}=\frac{x^3+16x}{x^3-1}. \]
Valutando il limite per \(x\to +\infty\) (e analogamente per \(x\to -\infty\), poiché i termini di grado massimo dominano in entrambi i casi):
\[ m=\lim_{x\to\pm\infty}\frac{x^3+16x}{x^3-1}=\frac{1+0}{1-0}=1. \]
Calcolo di \(q\)
Ora calcoliamo
\[ g(x)-mx=\frac{x^4+16x^2}{x^3-1}-x=\frac{x^4+16x^2-x^4+x}{x^3-1}=\frac{16x^2+x}{x^3-1}. \]
\[ q=\lim_{x\to\pm\infty}\frac{16x^2+x}{x^3-1}=0, \] \end{math}
Conclusione
Poiché i limiti danno lo stesso valore per \(x\to+\infty\) e per \(x\to-\infty\), risulta
\[ m=1,\qquad q=0, \]
quindi la retta \( \displaystyle y = x \) è un asintoto obliquo della funzione \(g(x)\) (oltre all'asintoto verticale in \(x=1\) già identificato).
7️⃣ Intersezioni con l'asintoto obliquo \(y=x\)
Risolviamo \(g(x)=x\):
\[ \frac{x^4+16x^2}{x^3-1}=x \Longrightarrow x^4+16x^2 = x^4 - x \Longrightarrow 16x^2 = -x. \]
Da cui:
\[ x(16x+1)=0 \Longrightarrow x=0 \ \text{o}\ x=-\tfrac{1}{16}. \]
Quindi le intersezioni con l'asintoto \(y=x\) sono i punti \((0,0)\) e \(\left(-\tfrac{1}{16}, -\tfrac{1}{16}\right)\) (entrambi validi poiché diversi da \(x=1\)).
8️⃣ Riepilogo qualitativo
Caratteristiche sintetiche del grafico
Questi elementi devono essere visibili nel grafico: due rami separati dall'asintoto verticale in \(x=1\), il ramo sinistro sotto l'asse \(x\) passando per l'origine e tendente a \(-\infty\) verso \(x\to1^-\), il ramo destro positivo che parte da \(+\infty\) appena a destra di \(x=1\) e si allinea alla direzione \(y=x\) per \(x\to+\infty\).
Un grafico probabile della funzione è il seguente:
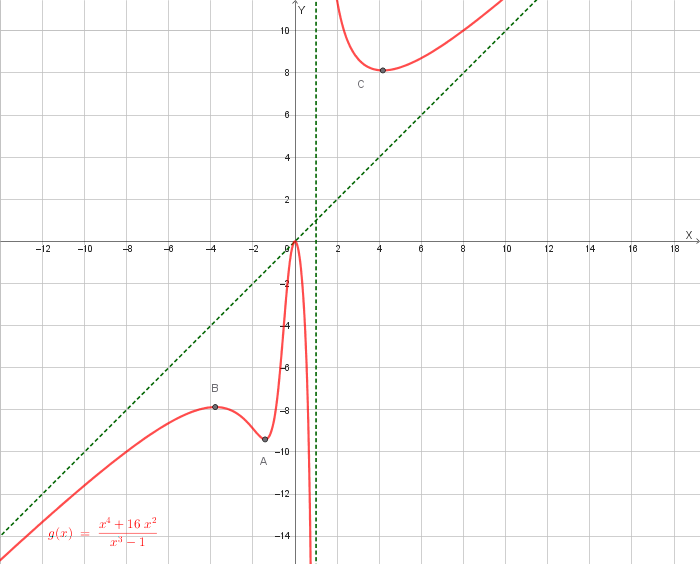
Dopo aver spiegato come si ottiene il grafico di una funzione \( f(|x|) \) a partire dal grafico di \( f(x) \), verifica che la funzione trovata nell’Esercizio 1, \[ f(x) = \frac{x^4 + 16x^2}{(|x|)^3 - 1}, \] coincide con \( g(|x|) \), essendo \( g \) la funzione indicata nell’Esercizio 2: \[ g(x) = \frac{x^4 + 16x^2}{x^3 - 1}. \] Spiega come si ottiene il grafico di \( f(x) \) a partire dal grafico di \( g(x) \) e rappresentalo.
1️⃣ Verifica che \( f(x) = g(|x|) \)
Partiamo dalla funzione definita nell’Esercizio 2: \[ g(x) = \frac{x^4 + 16x^2}{x^3 - 1}. \] Calcoliamo ora \( g(|x|) \): \[ g(|x|) = \frac{(|x|)^4 + 16(|x|)^2}{(|x|)^3 - 1}. \] Poiché \((|x|)^2 = x^2\) e \((|x|)^4 = x^4\), possiamo semplificare: \[ g(|x|) = \frac{x^4 + 16x^2}{(|x|)^3 - 1}. \] Ma questa è proprio la funzione trovata nell’Esercizio 1: \[ f(x) = \frac{x^4 + 16x^2}{(|x|)^3 - 1}. \] Conclusione: \( f(x) = g(|x|) \).
2️⃣ Effetto del valore assoluto sul grafico
Per costruire il grafico di una funzione del tipo \( y = f(|x|) \) a partire da quello di \( y = f(x) \), si procede in due passaggi:
In altre parole, ogni punto del grafico con ascissa positiva viene “riflesso” nel semipiano sinistro con la stessa ordinata.
3️⃣ Applicazione al caso della funzione data
Poiché \( f(x) = g(|x|) \), il ramo di \( f(x) \) per \( x > 0 \) coincide esattamente con il ramo destro del grafico di \( g(x) \), mentre il ramo per \( x < 0 \) è la sua immagine simmetrica rispetto all’asse \( y \).
4️⃣ Conseguenze sul grafico
5️⃣ Rappresentazione grafica
Il grafico di \( f(x) \) si ottiene dunque lasciando inalterato il ramo destro della funzione \( g(x) \) e ribaltandolo rispetto all'asse \(y\). Il risultato è una curva simmetrica con due asintoti verticali in \( x = -1 \) e \( x = 1 \) ed un asintototo obliquo \(y=x\) per \( x \to +\infty \).
Il grafico risultante della funzione è il seguente:
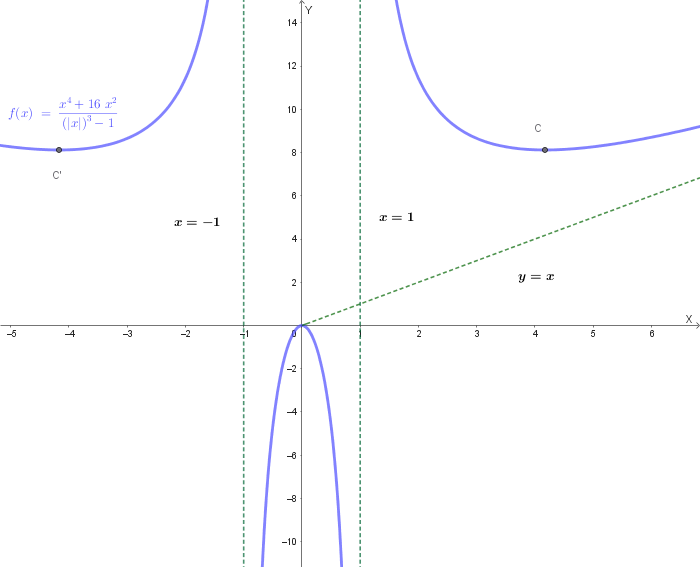
Si scriva l’equazione della curva simmetrica \( p' \) della parabola \( p \) rispetto all’asse delle \(x\) e si spieghi perché \( p \) e \( p' \) sono anche simmetriche rispetto all’origine degli assi.
1️⃣ Equazione della parabola data
La parabola assegnata nell’Esercizio 1 è: \[ p:\; y = \frac{1}{4}x^2 - 1. \]
2️⃣ Simmetria rispetto all’asse delle \(x\)
Per ottenere la curva \( p' \), simmetrica di \( p \) rispetto all’asse delle \(x\), basta cambiare di segno la coordinata \(y\) in ogni punto della curva originale. Ciò equivale a sostituire \( y \) con \(-y\) nell’equazione della parabola:
Moltiplicando per \(-1\), si ottiene: \[ p':\; y = -\frac{1}{4}x^2 + 1. \]
3️⃣ Relazione di simmetria tra \(p\) e \(p'\)
Osserviamo che: \[ p:\; y = \tfrac{1}{4}x^2 - 1, \quad p':\; y = -\tfrac{1}{4}x^2 + 1. \] La seconda equazione si ottiene dalla prima non solo cambiando il segno di \(y\), ma anche invertendo il segno del termine noto. In effetti, se si applica una **simmetria rispetto all’origine** (cioè si sostituisce \(x\) con \(-x\) e \(y\) con \(-y\)), si ha: \[ y = -\tfrac{1}{4}(-x)^2 + 1 = -\tfrac{1}{4}x^2 + 1, \] che è proprio l’equazione di \(p'\).
Conclusione: le due parabole \(p\) e \(p'\) sono:
4️⃣ Rappresentazione grafica
Rappresentiamo graficamente le due curve \(p\) e \(p'\) nello stesso sistema di riferimento:
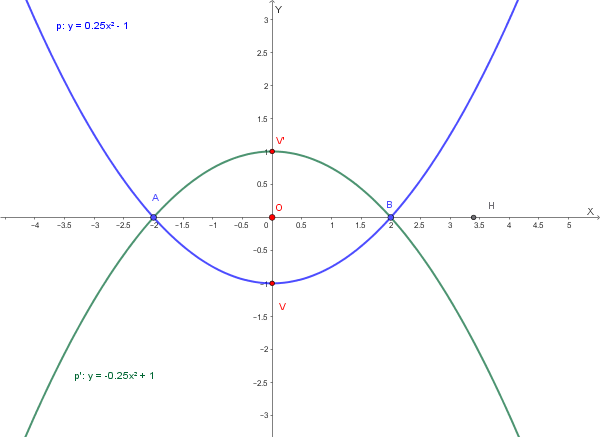
Si calcoli l'area della regione compresa tra le due parabole \(p\) e \(p'\).
1️⃣ Dati e osservazioni preliminari
Riprendiamo le parabole usate nei precedenti esercizi: \[ p:\; y=\tfrac{1}{4}x^2-1,\qquad p':\; y=-\tfrac{1}{4}x^2+1. \] Esse si intersecano con l'asse \(x\) nei punti \(A(-2,0)\) e \(B(2,0)\). Il vertice di \(p'\) è \(V'(0,1)\) e il vertice di \(p\) è \(V(0,-1)\). La retta che taglia entrambe le parabole e individua la corda considerata è l'asse \(x\): \(y=0\).
Figura:
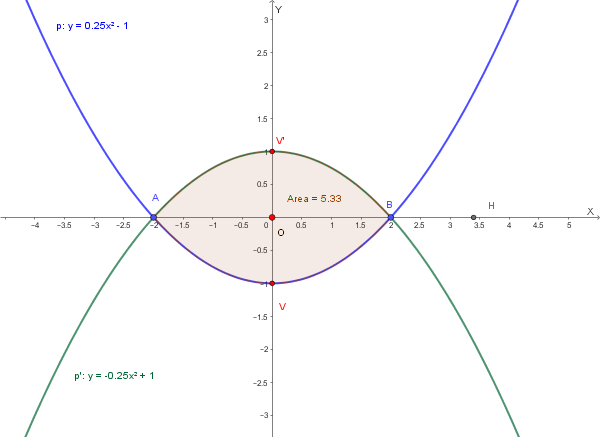
2️⃣ Enunciato del Teorema di Archimede
Se un segmento parabolico è delimitato da una parabola, da una corda \(AB\) e dal vertice corrispondente, l'area del segmento è \[ \text{Area}_{\text{segmento}}=\tfrac{2}{3}\cdot\text{Area}_{\text{rettangolo circoscritto}}, \] dove il rettangolo circoscritto ha per base la corda \(AB\) e per altezza la distanza tra la corda stessa e la tangente alla parabola parallela alla corda (nel nostro caso la tangente, orizzontale, nel vertice).
3️⃣ Costruzione del rettangolo circoscritto per \(p'\)
- La corda \(AB\) è il segmento sull'asse \(x\) tra \(-2\) e \(2\): base \(=4\).
- La tangente alla parabola \(p'\) parallela ad \(AB\) è la tangente orizzontale in corrispondenza del vertice \(V'(0,1)\), cioè la retta \(y=1\).
- La distanza tra la retta \(AB\) ( \(y=0\) ) e la tangente parallela ( \(y=1\) ) è quindi \(h=1\).
\[ \text{Area}_{\text{rettangolo}} = \text{base}\cdot \text{altezza} = 4\cdot 1 = 4. \]
4️⃣ Area del segmento parabolico superiore (tra \(p'\) e la corda \(AB\))
Applicando la formula di Archimede nella forma richiesta:
\[ \text{Area}_{\mathcal{S}'} = \tfrac{2}{3}\cdot \text{Area}_{\text{rettangolo}} = \tfrac{2}{3}\cdot 4 = \tfrac{8}{3}. \]
5️⃣ Area totale tra le due parabole
La regione cercata è costituita da due segmenti parabolici congruenti (quello superiore relativo a \(p'\) e quello inferiore relativo a \(p\)), dunque:
\[ \text{Area}_{\text{totale}} = 2\cdot \text{Area}_{\mathcal{S}'} = 2\cdot \tfrac{8}{3} = \tfrac{16}{3}. \]
Risultato finale:
\[ \boxed{\text{Area totale}=\dfrac{16}{3}} \]

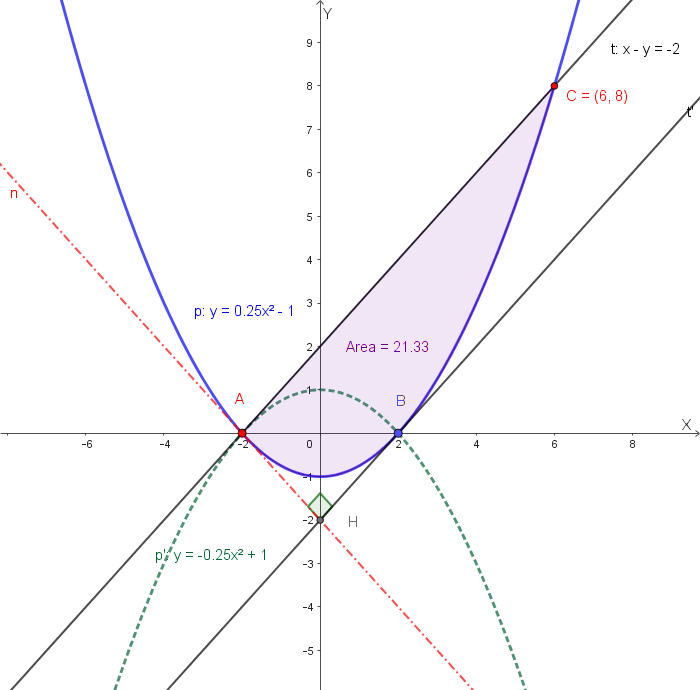
Si calcoli l'area della regione compresa fra la retta tangente a \(p'\) in \(A(-2,0)\) e la parabola \(p\).
1️⃣ Calcolo della tangente \(t\) a \(p'\) nel punto \(A(-2,0)\)
La parabola superiore è \(p': y=-\tfrac{1}{4}x^2+1\).
La derivata è \(y'=-\tfrac{1}{2}x\).
In \(x_A=-2\) risulta \(y'_A=-\tfrac{1}{2}\cdot(-2)=1\).
Quindi la tangente in \(A\) ha coefficiente angolare \(m=1\) e passa per \(A(-2,0)\):
\[ t:\; y-0 = 1(x+2) \quad\Rightarrow\quad y = x+2. \]
N.B. Il valore del coefficiente angolare della retta tangente in \(A\) si può anche ottenere facendo sistema tra la parabola ed il fascio di rette di centro \(A\), e ponendo il discriminante dell'equazione risolvente uguale a zero.
2️⃣ Calcolo della tangente \(t'\) a \(p\) parallela a \(t\) (necessaria per calcolare l'area del rettangolo circoscritto al segmento parabolico individuato dalla retta \(t\) e dalla parabola \(p\))
La parabola inferiore è \(p:\; y=\tfrac{1}{4}x^2-1\).
Derivando: \(y'=\tfrac{1}{2}x\).
Cerchiamo il punto di \(p\) in cui la tangente abbia la stessa pendenza \(m=1\):
\[
\tfrac{1}{2}x=1 \Rightarrow x=2.
\]
In \(x=2\), \(y=\tfrac{1}{4}\cdot4-1=0\), quindi il punto di tangenza è \(B(2,0)\).
La tangente cercata è
\[ t':\; y-0=1(x-2) \Rightarrow y=x-2. \]
N.B. Siccome le due parabole sono simmetriche rispetto all'origine degli assi, e \(B\) è il simmetrico di \(A\) rispetto all'origine, la tangente \(t'\) è la simmetrica di \(t\) ripetto all'origine, quindi è la retta che passa per \(B\) con coefficiente angolare \(1\).
Facendo i calcoli si ottiene:
\[ t:\; y-0=1(x-2) \Rightarrow y=x-2. \]
3️⃣ Distanza fra le due rette parallele \(t\) e \(t'\)
Le rette hanno equazioni \(t: y = x + 2\) e \(t': y = x - 2\).
Poiché sono parallele, la loro distanza è costante; possiamo calcolarla come distanza del punto \(A(-2,0)\) da \(t'\).
Scriviamo \(t'\) in forma implicita: \(x - y - 2 = 0\).
Applicando la formula della distanza di un punto \(P(x_0, y_0)\) da una retta \(ax + by + c = 0\):
\[ d = \frac{|a x_0 + b y_0 + c|}{\sqrt{a^2 + b^2}}. \]
Sostituendo \(a = 1\), \(b = -1\), \(c = -2\) e \(A(-2,0)\):
\[ AH = d(A,t') = \frac{|1\cdot(-2) + (-1)\cdot0 - 2|}{\sqrt{1^2 + (-1)^2}} = \frac{|-4|}{\sqrt{2}} = \frac{4}{\sqrt{2}} = 2\sqrt{2}. \]
Quindi la distanza tra le due rette parallele \(t\) e \(t'\) è \(AH = 2\sqrt{2}\).
4️⃣ Intersezione \(C\) fra la parabola \(p\) e la tangente \(t\)
Risolviamo il sistema: \[ \begin{cases} y = \tfrac{1}{4}x^2 - 1 \\ y = x + 2 \end{cases} \Rightarrow \tfrac{1}{4}x^2 - 1 = x + 2. \] Moltiplichiamo per 4: \[ x^2 - 4x - 12 = 0 \Rightarrow (x-6)(x+2)=0. \] Uno dei punti d’intersezione è proprio \(A(-2,0)\); l’altro è \(C(6,8)\).
5️⃣ Distanza \(AC\)
\[ AC = \sqrt{(6 - (-2))^2 + (8 - 0)^2} = \sqrt{8^2 + 8^2} = 8\sqrt{2}. \]
6️⃣ Applicazione del Teorema di Archimede
Consideriamo il rettangolo circoscritto avente lati \(AC\) e \(AH\). Quindi l'area del rettangolo è
\[ \text{Area}_{\text{rettangolo}} = AC\cdot AH = (8\sqrt{2})\cdot(2\sqrt{2}) = 8\cdot 2 \cdot (\sqrt{2}\sqrt{2}) = 16\cdot 2 = 32. \]
Per il Teorema di Archimede: Area(segmento parabolico) = \(\tfrac{2}{3}\) (dell'area del rettangolo circoscritto),
\[ \text{Area} = \tfrac{2}{3}\cdot 32 = \tfrac{64}{3}. \]
Risultato finale:
\[ \boxed{\text{Area della regione fra la tangente a }p'\text{ in }A\text{ e la parabola }p \;=\; \dfrac{64}{3}} \]
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.