



Questo compito è stato assegnato il giorno 12 Dicembre 1991 a una classe 5ª del Liceo Scientifico.
Argomenti: Problema con un limite, Limiti notevoli, Problema sui luoghi geometrici, Studio di funzione logaritmica.
Data una semicirconferenza di diametro AC = 2 e centro O, traccia la semiretta uscente da A, perpendicolare ad AC e giacente rispetto ad AC dalla stessa parte della semicirconferenza.
Detto M un punto generico su tale semiretta (distinto da A), traccia da esso l'ulteriore tangente MB alla semicirconferenza. Detta K l'ulteriore intersezione della semicirconferenza con la retta OM:
a) determina l'area \(y\) del quadrilatero ACBK in funzione dell'angolo \(\widehat{BAC} = x\);
b) Determina il valore di \(y\) quando \(x\) tende a \(\pi/4\) e spiega geometricamente il risultato ottenuto.
c) Dopo aver determinato i limiti geometrici dell'incognita, determina il valore dell'angolo \(x\) in modo che l'area del quadrilatero \(ACBK\) valga \(\frac{3\sqrt{3}}{4}\).
Figura rappresentativa del problema:
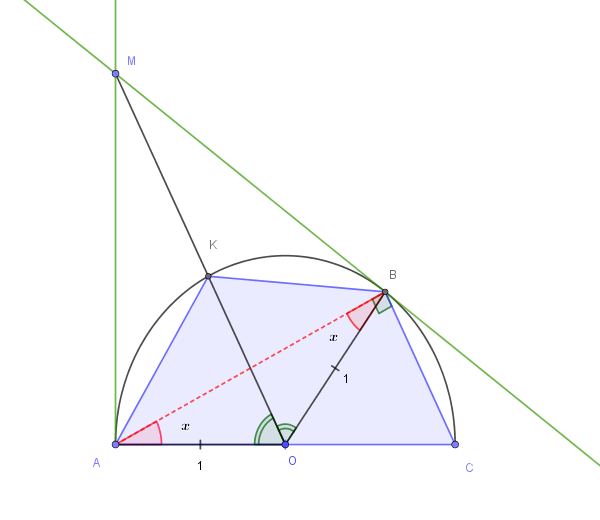
Prima di calcolare l'area, definiamo i limiti geometrici dell'angolo \(x = \widehat{BAC}\), ricordando che \(M\) è un punto della semiretta uscente da \(A\) distinto da \(A\):
In sintesi, l'angolo varia nell'intervallo geometrico \(\mathbf{x \in (0, \pi/2)}\).
Suddividiamo quindi l'area \(y\) nella somma delle aree dei triangoli \(\triangle AOK\), \(\triangle BOK\) e \(\triangle BOC\).
Il raggio della semicirconferenza è \(\mathbf{r = \overline{OA} = \overline{OB} = \overline{OK} = \overline{OC} = 1}\).
Calcoliamo il valore della funzione quando \(x = \pi/4\):
\[ y = f(x) = \cos(x) \,(1 + \sin(x)) \] \[ f\!\left(\frac{\pi}{4}\right) = \cos\frac{\pi}{4} \left(1 + \sin\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} \left(1 + \frac{\sqrt{2}}{2}\right) \approx 1.207 \]Significato geometrico: quando \(x = \pi/4\), il segmento \(AM\) è uguale al raggio della semicirconferenza. In questa configurazione, la tangente \(MB\) risulta parallela al diametro \(AC\), e il lato \(BC\) coincide con il lato del quadrato inscritto nella circonferenza di raggio \( 1 \). L’area \(y \approx 1.207\) rappresenta quindi l'area del quadrilatero \(ACBK\) quando \(x = \pi/4\).
Vogliamo trovare \(x \in (0, \tfrac{\pi}{2})\) tale che l'area del quadrilatero \(ACBK\) sia:
\[ y = f(x) = \cos(x) \,(1 + \sin(x)) = \frac{3\sqrt{3}}{4}. \]Sviluppo:
\[ \cos(x) + \cos(x)\sin(x) = \frac{3\sqrt{3}}{4} \]Sostituzione: Pongo \(t = \sin(x)\), con \(x \in (0, \frac{\pi}{2})\) quindi \(t \in (0, 1)\).
Dato che \(\cos(x) = \sqrt{1-t^2}\) (positivo in \((0, \frac{\pi}{2})\)), sostituisco:
\[ \sqrt{1-t^2} + t\sqrt{1-t^2} = \frac{3\sqrt{3}}{4} \] \[ \sqrt{1-t^2}(1 + t) = \frac{3\sqrt{3}}{4} \]Elevo al quadrato:
\[ (1-t^2)(1+t)^2 = \frac{27}{16} \]Sviluppo:
\[ (1-t)(1+t)(1+t)^2 = (1-t)(1+t)^3 \]Espandendo \((1+t)^3 = 1 + 3t + 3t^2 + t^3\):
\[ (1-t)(1 + 3t + 3t^2 + t^3) = \frac{27}{16} \] \[ 1 + 3t + 3t^2 + t^3 - t - 3t^2 - 3t^3 - t^4 = \frac{27}{16} \] \[ 1 + 2t - 2t^3 - t^4 = \frac{27}{16} \]Moltiplico per 16:
\[ 16 + 32t - 32t^3 - 16t^4 = 27 \] \[ 16t^4 + 32t^3 - 32t + 11 = 0 \]Ricerca di una radice: Devo trovare una soluzione nell'intervallo \((0, 1)\). Provo con valori semplici.
Per \(t = \frac{1}{2}\):
\[ 16 \cdot \frac{1}{16} + 32 \cdot \frac{1}{8} - 32 \cdot \frac{1}{2} + 11 = 1 + 4 - 16 + 11 = 0 \quad \checkmark \]Quindi \(t = \frac{1}{2}\) è una radice.
Prima fattorizzazione: Dividendo per \((2t-1)\) ottengo:
\[ 16t^4 + 32t^3 - 32t + 11 = (2t-1)(8t^3 + 20t^2 + 10t - 11) \]Ricerca di una radice del polinomio cubico: Devo verificare se \(8t^3 + 20t^2 + 10t - 11 = 0\) ha soluzioni in \((0, 1)\).
Provo con \(t = \frac{1}{2}\):
\[ 8 \cdot \frac{1}{8} + 20 \cdot \frac{1}{4} + 10 \cdot \frac{1}{2} - 11 = 1 + 5 + 5 - 11 = 0 \quad \checkmark \]Quindi anche \(t = \frac{1}{2}\) è radice del polinomio cubico.
Seconda fattorizzazione: Dividendo nuovamente per \((2t-1)\):
\[ 8t^3 + 20t^2 + 10t - 11 = (2t-1)(4t^2 + 12t + 11) \]Quindi:
\[ (2t-1)^2(4t^2 + 12t + 11) = 0 \]Analisi delle soluzioni:
Discriminante: \(\Delta = 144 - 4(4)(11) = 144 - 176 = -32 < 0\)
Nessuna soluzione reale.
Conclusione:
L'unica soluzione è \(t = \frac{1}{2}\), quindi:
\[ \sin(x) = \frac{1}{2} \]Con \(x \in (0, \frac{\pi}{2})\):
\[ \boxed{x = \frac{\pi}{6}} \]Trovare l'equazione del luogo dei punti medi delle corde staccate dalle rette del fascio di equazione \(y = mx\) sulla circonferenza di equazione:
\[x^2 + y^2 - 8x = 0\]
La circonferenza data ha centro \(C = (4, 0)\) e raggio \(R = 4\) (distanza di \(C\) dall'origine, che è un punto della circonferenza).
Rappresentiamo la circonferenza data insieme ad una generica retta del fascio \(y = mx\) ed indichiamo con \(A\) l'ulteriore intersezione (l'altra è \(O\)) della retta con la circonferenza.
Rappresentazione grafica della circonferenza e del punto medio \(M\) di \(OA\):
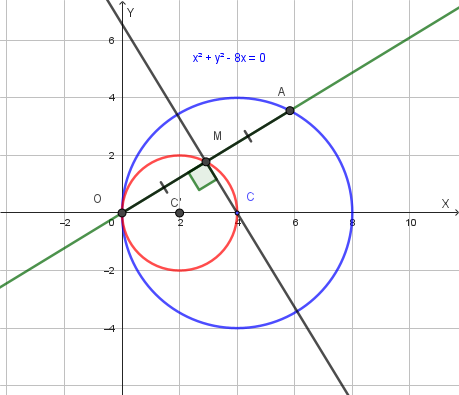
Metodo 1: Coordinate del punto medio
Troviamo le coordinate del punto medio \(M\) della corda \(OA\).
Sostituendo \(y = mx\) nell'equazione della circonferenza:
\[x^2 + (mx)^2 - 8x = 0\] \[x^2(1 + m^2) - 8x = 0\] \[x(x(1 + m^2) - 8) = 0\]Le soluzioni sono \(x = 0\) (punto \(O\)) e \(x = \frac{8}{1 + m^2}\) (punto \(A\)).
Le coordinate di \(A\) sono:
\[A = \left(\frac{8}{1 + m^2}, \frac{8m}{1 + m^2}\right)\]Il punto medio \(M\) di \(OA\) ha coordinate:
\[M = \left(\frac{4}{1 + m^2}, \frac{4m}{1 + m^2}\right)\]Equazioni parametriche del luogo:
\[\begin{cases} x = \frac{4}{1 + m^2}\\ y = \frac{4m}{1 + m^2} \end{cases}\]Eliminazione del parametro \(m\):
Dalla prima equazione: \(1 + m^2 = \frac{4}{x}\), da cui \(m^2 = \frac{4}{x} - 1 = \frac{4 - x}{x}\)
Dalla seconda equazione: \(m = \frac{y(1 + m^2)}{4} = \frac{y}{4} \cdot \frac{4}{x} = \frac{y}{x}\)
Quindi: \(m^2 = \frac{y^2}{x^2}\)
Uguagliando le due espressioni di \(m^2\):
\[\frac{y^2}{x^2} = \frac{4 - x}{x}\] \[y^2 = x(4 - x)\] \[y^2 = 4x - x^2\] \[\boxed{x^2 + y^2 - 4x = 0}\]Soluzione alternativa sintetica:
Per una nota proprietà della circonferenza, \(CM\) è perpendicolare alla corda \(OA\). Il generico angolo \(\widehat{OMC}\) è quindi retto, pertanto \(M\) varia sulla circonferenza di diametro \(OC\), perché descrive il luogo dei punti che vedono il segmento \(OC\) sotto un angolo retto.
La circonferenza di diametro \(OC\) ha centro \(C' = (2, 0)\) e raggio \(R' = 2\), quindi ha equazione:
\[(x - 2)^2 + (y - 0)^2 = 4\]da cui:
\[\boxed{x^2 + y^2 - 4x = 0}\]Soluzione alternativa con l'omotetia:
Osserviamo che il punto \(M\) è il punto medio della corda \(OA\), dove \(A\) è un punto della circonferenza data. Questo significa che \(M\) divide il segmento \(OA\) nel rapporto \(1:1\), ovvero:
\[\overrightarrow{OM} = \frac{1}{2}\overrightarrow{OA}\]Quindi il luogo descritto da \(M\) è la figura corrispondente della circonferenza data nell'omotetia di centro \(O\) e rapporto di omotetia \(k = \frac{1}{2}\).
Nell'omotetia di centro \(O = (0, 0)\) e rapporto \(k = \frac{1}{2}\):
Pertanto, il luogo dei punti medi è la circonferenza di centro \(C' = (2, 0)\) e raggio \(R' = 2\), con equazione:
\[(x - 2)^2 + y^2 = 4\]da cui:
\[\boxed{x^2 + y^2 - 4x = 0}\]Calcola i seguenti limiti:
a) \(\displaystyle\lim_{x \to 0} \frac{x^2}{1 - \cos(3x)}\)
b) \(\displaystyle\lim_{x \to +\infty} \left(\sqrt{x^2 + 4x} - \sqrt{x^2 - 3}\right)\)
c) \(\displaystyle\lim_{x \to +\infty} \left(\frac{x-1}{x+3}\right)^{x+2}\)
d) \(\displaystyle\lim_{x \to 0} \frac{\ln(\cos(x))}{\arcsin(\sin(x^2))}\)
e) \(\displaystyle\lim_{x \to 0} \frac{\sqrt{1+\sin(x)}-1}{e^x-1}\)
Utilizzando il limite notevole
Sappiamo che \(\displaystyle\lim_{t \to 0} \frac{1 - \cos(t)}{t^2} = \frac{1}{2}\)
Riscriviamo il limite:
\[ \lim_{x \to 0} \frac{x^2}{1 - \cos(3x)} = \lim_{x \to 0} \frac{x^2}{(3x)^2} \cdot \frac{(3x)^2}{1 - \cos(3x)} \] \[ = \lim_{x \to 0} \frac{x^2}{9x^2} \cdot \frac{(3x)^2}{1 - \cos(3x)} = \frac{1}{9} \cdot \lim_{x \to 0} \frac{(3x)^2}{1 - \cos(3x)} \]Ponendo \(t = 3x\), quando \(x \to 0\) si ha \(t \to 0\), quindi:
\[ \lim_{x \to 0} \frac{(3x)^2}{1 - \cos(3x)} = \lim_{t \to 0} \frac{t^2}{1 - \cos(t)} = \frac{1}{\lim_{t \to 0} \frac{1 - \cos(t)}{t^2}} = \frac{1}{\frac{1}{2}} = 2 \]Pertanto:
\[ \lim_{x \to 0} \frac{x^2}{1 - \cos(3x)} = \frac{1}{9} \cdot 2 = \boxed{\frac{2}{9}} \]Forma indeterminata: \(\infty - \infty\)
Razionalizzazione: Moltiplichiamo e dividiamo per il coniugato:
\[ \lim_{x \to +\infty} \left(\sqrt{x^2 + 4x} - \sqrt{x^2 - 3}\right) \cdot \frac{\sqrt{x^2 + 4x} + \sqrt{x^2 - 3}}{\sqrt{x^2 + 4x} + \sqrt{x^2 - 3}} \] \[ = \lim_{x \to +\infty} \frac{(x^2 + 4x) - (x^2 - 3)}{\sqrt{x^2 + 4x} + \sqrt{x^2 - 3}} \] \[ = \lim_{x \to +\infty} \frac{4x + 3}{\sqrt{x^2 + 4x} + \sqrt{x^2 - 3}} \]Raccogliamo \(x\) al numeratore e \(x\) sotto le radici al denominatore:
\[ = \lim_{x \to +\infty} \frac{x(4 + \frac{3}{x})}{x\sqrt{1 + \frac{4}{x}} + x\sqrt{1 - \frac{3}{x^2}}} \] \[ = \lim_{x \to +\infty} \frac{x(4 + \frac{3}{x})}{x\left(\sqrt{1 + \frac{4}{x}} + \sqrt{1 - \frac{3}{x^2}}\right)} \] \[ = \lim_{x \to +\infty} \frac{4 + \frac{3}{x}}{\sqrt{1 + \frac{4}{x}} + \sqrt{1 - \frac{3}{x^2}}} \]Calcoliamo il limite:
\[ = \frac{4 + 0}{\sqrt{1 + 0} + \sqrt{1 - 0}} = \frac{4}{1 + 1} = \frac{4}{2} = \boxed{2} \]Forma indeterminata: \(1^\infty\)
Riscriviamo la base:
\[ \frac{x-1}{x+3} = \frac{x+3-4}{x+3} = 1 - \frac{4}{x+3} \]Il limite diventa:
\[ \lim_{x \to +\infty} \left(1 - \frac{4}{x+3}\right)^{x+2} \]Utilizziamo il limite notevole: \(\displaystyle\lim_{t \to 0} (1 + t)^{\frac{1}{t}} = e\)
Poniamo \(t = -\frac{4}{x+3}\), quindi quando \(x \to +\infty\) si ha \(t \to 0\) e \(x+3 = -\frac{4}{t}\):
\[ \lim_{x \to +\infty} \left(1 - \frac{4}{x+3}\right)^{x+2} = \lim_{x \to +\infty} \left(1 + t\right)^{x+2} \]Riscriviamo l'esponente:
\[ x+2 = (x+3) - 1 = -\frac{4}{t} - 1 \]Quindi:
\[ \lim_{t \to 0} (1 + t)^{-\frac{4}{t} - 1} = \lim_{t \to 0} (1 + t)^{-\frac{4}{t}} \cdot (1 + t)^{-1} \] \[ = \lim_{t \to 0} \left[(1 + t)^{\frac{1}{t}}\right]^{-4} \cdot \lim_{t \to 0} (1 + t)^{-1} \] \[ = e^{-4} \cdot 1 = \boxed{e^{-4} = \frac{1}{e^4}} \]Forma indeterminata: \(\frac{0}{0}\)
Semplifichiamo usando i limiti notevoli:
Numeratore:
\[ \ln(\cos(x)) = \ln(1 + (\cos(x) - 1)) \]Usando il limite notevole \(\ln(1 + t) \sim t\) per \(t \to 0\):
\[ \ln(\cos(x)) \sim \cos(x) - 1 \quad \text{per } x \to 0 \]Denominatore:
Usando i limiti notevoli \(\arcsin(t) \sim t\) e \(\sin(t) \sim t\) per \(t \to 0\):
\[ \arcsin(\sin(x^2)) \sim \sin(x^2) \sim x^2 \quad \text{per } x \to 0 \]Il limite si riconduce a:
\[ \lim_{x \to 0} \frac{\ln(\cos(x))}{\arcsin(\sin(x^2))} = \lim_{x \to 0} \frac{\cos(x) - 1}{x^2} \]Sappiamo che \(\displaystyle\lim_{x \to 0} \frac{\cos(x) - 1}{x^2} = -\frac{1}{2}\)
Forma indeterminata: \(\frac{0}{0}\)
Semplifichiamo usando i limiti notevoli:
Numeratore:
Riscriviamo \(\sqrt{1+\sin(x)} = (1+\sin(x))^{1/2}\) e usiamo il limite notevole:
\[ \lim_{t \to 0} \frac{(1+t)^k - 1}{t} = k \]Ponendo \(t = \sin(x)\) e \(k = \frac{1}{2}\):
\[ \sqrt{1+\sin(x)}-1 = (1+\sin(x))^{1/2} - 1 \sim \frac{1}{2}\sin(x) \quad \text{per } x \to 0 \]Denominatore:
Usando il limite notevole \(e^x - 1 \sim x\) per \(x \to 0\):
\[ e^x - 1 \sim x \]Il limite si riconduce a:
\[ \lim_{x \to 0} \frac{\sqrt{1+\sin(x)}-1}{e^x-1} = \lim_{x \to 0} \frac{\frac{1}{2}\sin(x)}{x} = \frac{1}{2} \lim_{x \to 0} \frac{\sin(x)}{x} \]Usando il limite notevole \(\displaystyle\lim_{x \to 0} \frac{\sin(x)}{x} = 1\):
\[ = \frac{1}{2} \cdot 1 = \boxed{\frac{1}{2}} \]Data la seguente funzione:
\[y = f(x) = \log_2\left(\frac{2x-1}{x+2}\right)\]
a) Trova il dominio e stabilisci se in base ad esso è possibile escludere la parità o disparità della funzione.
b) Servendoti della definizione, stabilisci se la funzione è pari o dispari.
c) Trova il segno della funzione e eventuali intersezioni con gli assi cartesiani.
d) Rappresenta le zone del piano in cui si troverà il grafico della funzione.
e) Calcola i limiti della funzione agli estremi del dominio.
f) Calcola la derivata prima della funzione, stabilisci dove è crescente, dove è decrescente e indica eventuali massimi e minimi relativi.
g) Senza studiare la derivata seconda indica il grafico più probabile della funzione.
Condizione di esistenza del logaritmo:
Il logaritmo esiste se e solo se l'argomento è positivo:
\[\frac{2x-1}{x+2} > 0\]Studio del segno della frazione:
Tabella dei segni:
| x | −∞ | −2 | 1/2 | +∞ | |||
| 2x−1 | − | − | 0 | + | |||
| x+2 | − | 0 | + | + | |||
| (2x−1)/(x+2) | + | ∄ | − | ∄ | + |
Dominio:
\[\boxed{D: x \in (-\infty, -2) \cup \left(\frac{1}{2}, +\infty\right)}\]Simmetria del dominio:
Il dominio NON è simmetrico rispetto all'origine (se \(x \in D\) non è detto che \(-x \in D\)). Ad esempio, \(x = 1 \in D\) ma \(-1 \notin D\) perché \(-1 \in (-2, \frac{1}{2})\).
Conclusione: Poiché il dominio non è simmetrico rispetto all'origine, la funzione non può essere né pari né dispari.
Studio del segno:
\(f(x) > 0\) quando \(\log_2\left(\frac{2x-1}{x+2}\right) > 0\)
Ciò accade quando:
\[\frac{2x-1}{x+2} > 1\] \[\frac{2x-1}{x+2} - 1 > 0\] \[\frac{2x-1-(x+2)}{x+2} > 0\] \[\frac{x-3}{x+2} > 0\]Punti critici:
Tabella dei segni di \(\frac{x-3}{x+2}\):
| x | −∞ | −2 | 3 | +∞ | |||
| x−3 | − | − | 0 | + | |||
| x+2 | − | 0 | + | + | |||
| (x−3)/(x+2) | + | ∄ | − | 0 | + |
Ricordando il dominio \(D: (-\infty, -2) \cup \left(\frac{1}{2}, +\infty\right)\):
Tabella del segno di \(f(x)\) nel dominio:
| x | −∞ | −2 | ✘ | 1/2 | 3 | +∞ | |||
| f(x) | + | ∄ | ∄ | ∄ | − | 0 | + |
Conclusione sul segno:
Intersezioni con gli assi:
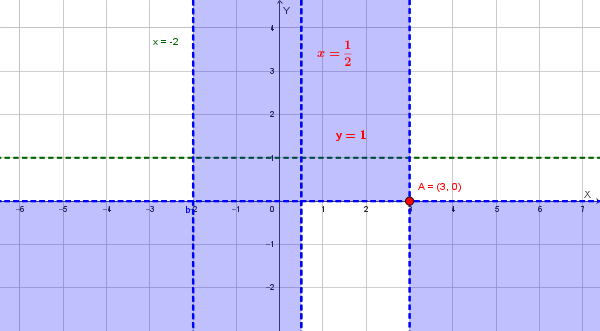
Dal dominio e dallo studio del segno possiamo individuare le zone del piano in cui si trova il grafico:
Il grafico della funzione si trova nelle zone chiare del seguente grafico:
Limite per \(x \to -2^-\):
\[\lim_{x \to -2^-} \log_2\left(\frac{2x-1}{x+2}\right)\]Numeratore: \(2(-2)-1 = -5 < 0\)
Denominatore: \(x+2 \to 0^-\)
Quindi: \(\frac{2x-1}{x+2} \to +\infty\)
\[\boxed{\lim_{x \to -2^-} f(x) = +\infty}\]Asintoto verticale: \(x = -2\)
Limite per \(x \to \left(\frac{1}{2}\right)^+\):
\[\lim_{x \to \left(\frac{1}{2}\right)^+} \log_2\left(\frac{2x-1}{x+2}\right)\]Numeratore: \(2 \cdot \frac{1}{2} - 1 = 0^+\)
Denominatore: \(\frac{1}{2} + 2 = \frac{5}{2} > 0\)
Quindi: \(\frac{2x-1}{x+2} \to 0^+\)
\[\boxed{\lim_{x \to \left(\frac{1}{2}\right)^+} f(x) = -\infty}\]Asintoto verticale: \(x = \frac{1}{2}\)
Limite per \(x \to -\infty\):
\[\lim_{x \to -\infty} \log_2\left(\frac{2x-1}{x+2}\right) = \log_2\left(\lim_{x \to -\infty}\frac{2x-1}{x+2}\right)\] \[= \log_2\left(\lim_{x \to -\infty}\frac{2-\frac{1}{x}}{1+\frac{2}{x}}\right) = \log_2(2) = \boxed{1}\]Asintoto orizzontale: \(y = 1\)
Limite per \(x \to +\infty\):
\[\lim_{x \to +\infty} \log_2\left(\frac{2x-1}{x+2}\right) = \log_2(2) = \boxed{1}\]Asintoto orizzontale: \(y = 1\)
Calcolo della derivata:
\[f(x) = \log_2\left(\frac{2x-1}{x+2}\right) = \frac{\ln\left(\frac{2x-1}{x+2}\right)}{\ln 2}\] \[f'(x) = \frac{1}{\ln 2} \cdot \frac{x+2}{2x-1} \cdot \frac{d}{dx}\left(\frac{2x-1}{x+2}\right)\]Derivata del quoziente:
\[\frac{d}{dx}\left(\frac{2x-1}{x+2}\right) = \frac{2(x+2) - (2x-1) \cdot 1}{(x+2)^2} = \frac{2x+4-2x+1}{(x+2)^2} = \frac{5}{(x+2)^2}\]Quindi:
\[f'(x) = \frac{1}{\ln 2} \cdot \frac{x+2}{2x-1} \cdot \frac{5}{(x+2)^2} = \frac{5}{(2x-1)(x+2) \ln 2}\]Studio del segno di \(f'(x)\):
Nel dominio \(D: (-\infty, -2) \cup \left(\frac{1}{2}, +\infty\right)\):
Conclusione:
Lo studio effettuato ci permette di indicare il grafico più probabile della funzione:
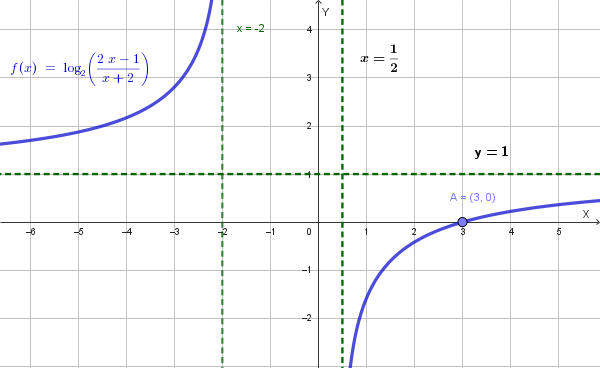
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.