Compito in Classe di Matematica

Soluzione Esercizio 1

Passo 1: Individuare la formula

Osserviamo la somma dei primi termini:

• Per \(n = 1\): \(\frac{1}{2} = \frac{1}{2}\)
• Per \(n = 2\): \(\frac{1}{2} + \frac{1}{4} = \frac{2+1}{4} = \frac{3}{4}\)
• Per \(n = 3\): \(\frac{1}{2} + \frac{1}{4} + \frac{1}{8} = \frac{4+2+1}{8} = \frac{7}{8}\)

Ipotizziamo che la formula sia: \[S_n = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \ldots + \frac{1}{2^n} = 1 - \frac{1}{2^n}\]

Passo 2: Dimostrazione per induzione

Base dell'induzione (n = 1):

Per \(n = 1\): \(S_1 = \frac{1}{2}\)

Formula: \(1 - \frac{1}{2^1} = 1 - \frac{1}{2} = \frac{1}{2}\) ✓

Ipotesi induttiva:

Supponiamo che per un certo \(n \geq 1\) valga: \(S_n = 1 - \frac{1}{2^n}\)

Passo induttivo (n → n+1):

Dobbiamo dimostrare che \(S_{n+1} = 1 - \frac{1}{2^{n+1}}\)

Abbiamo:

\[S_{n+1} = S_n + \frac{1}{2^{n+1}}\]

Usando l'ipotesi induttiva:

\[S_{n+1} = \left(1 - \frac{1}{2^n}\right) + \frac{1}{2^{n+1}} = 1 - \frac{1}{2^n} + \frac{1}{2^{n+1}}\] \[= 1 - \frac{2}{2^{n+1}} + \frac{1}{2^{n+1}} = 1 - \frac{2-1}{2^{n+1}} = 1 - \frac{1}{2^{n+1}}\]

Conclusione:

Per il principio di induzione matematica, la formula \(\boxed{S_n = 1 - \frac{1}{2^n}}\) è valida per ogni \(n \geq 1\).

Soluzione Esercizio 2

Equazione da risolvere:

\[\frac{1-\cos(2x)}{1+\cos(2x)} = \frac{\tan(x)}{2\cos(x)}\]

Passo 1: Condizioni di esistenza

Per l'esistenza dell'equazione dobbiamo avere:

• \(1 + \cos(2x) \neq 0 \Rightarrow \cos(2x) \neq -1 \Rightarrow 2x \neq \pi + 2k\pi \Rightarrow x \neq \frac{\pi}{2} + k\pi\)
• \(\cos(x) \neq 0\) (per l'esistenza di \(\tan(x)\) e per il denominatore) \(\Rightarrow x \neq \frac{\pi}{2} + k\pi\)

Quindi le condizioni di esistenza sono: \(x \neq \frac{\pi}{2} + k\pi\) con \(k \in \mathbb{Z}\)

Passo 2: Semplificare il membro sinistro

Utilizziamo le formule di duplicazione:

• \(\cos(2x) = \cos^2(x) - \sin^2(x) = 2\cos^2(x) - 1 = 1 - 2\sin^2(x)\)

Usando \(\cos(2x) = 1 - 2\sin^2(x)\):

\[1 - \cos(2x) = 1 - (1 - 2\sin^2(x)) = 2\sin^2(x)\]

Usando \(\cos(2x) = 2\cos^2(x) - 1\):

\[1 + \cos(2x) = 1 + (2\cos^2(x) - 1) = 2\cos^2(x)\]

Quindi il membro sinistro diventa:

\[\frac{1-\cos(2x)}{1+\cos(2x)} = \frac{2\sin^2(x)}{2\cos^2(x)} = \frac{\sin^2(x)}{\cos^2(x)} = \tan^2(x)\]

Passo 3: Semplificare il membro destro

\[\frac{\tan(x)}{2\cos(x)} = \frac{\frac{\sin(x)}{\cos(x)}}{2\cos(x)} = \frac{\sin(x)}{2\cos^2(x)}\]

Passo 4: Risolvere l'equazione semplificata

L'equazione diventa:

\[\tan^2(x) = \frac{\sin(x)}{2\cos^2(x)}\] \[\frac{\sin^2(x)}{\cos^2(x)} = \frac{\sin(x)}{2\cos^2(x)}\]

Moltiplicando entrambi i membri per \(\cos^2(x)\) (valido per le condizioni di esistenza):

\[\sin^2(x) = \frac{\sin(x)}{2}\]

Moltiplicando per 2:

\[2\sin^2(x) = \sin(x)\] \[2\sin^2(x) - \sin(x) = 0\] \[\sin(x)(2\sin(x) - 1) = 0\]

Passo 5: Trovare le soluzioni

Abbiamo due casi:

1. \(\sin(x) = 0 \Rightarrow x = k\pi\) con \(k \in \mathbb{Z}\)
2. \(2\sin(x) - 1 = 0 \Rightarrow \sin(x) = \frac{1}{2} \Rightarrow x = \frac{\pi}{6} + 2k\pi\) o \(x = \frac{5\pi}{6} + 2k\pi\) con \(k \in \mathbb{Z}\)

Passo 6: Verifica con le condizioni di esistenza

Tutte le soluzioni trovate soddisfano le condizioni di esistenza \(x \neq \frac{\pi}{2} + k\pi\).

Soluzione finale:

\[\boxed{x = k\pi \text{ oppure } x = \frac{\pi}{6} + 2k\pi \text{ oppure } x = \frac{5\pi}{6} + 2k\pi, \quad k \in \mathbb{Z}}\]

Soluzione Esercizio 3

Analisi del problema:

Il quadrato ABCD ha area 4, quindi lato \(l = 2\). La diagonale AC ha lunghezza \(\overline{AC} = l\sqrt{2} = 2\sqrt{2}\).

Calcolo delle lunghezze dei segmenti:

1° segmento (\(\overline{BE}\)):

E è il piede della perpendicolare da B alla diagonale AC. Poiché E è il punto medio di AC, abbiamo:

\(\overline{BE} = \frac{\overline{AC}}{2} = \frac{2\sqrt{2}}{2} = \sqrt{2}\)

Oppure: \(\overline{BE} = \frac{\overline{BC}}{\sqrt{2}} = \frac{2}{\sqrt{2}} = \sqrt{2}\)

2° segmento (\(\overline{EF}\)):

F è il piede della perpendicolare da E al lato AB.

\(\overline{EF} = \frac{\overline{BE}}{\sqrt{2}} = \frac{\sqrt{2}}{\sqrt{2}} = 1\)

3° segmento (\(\overline{FG}\)):

G è il piede della perpendicolare da F alla diagonale AC.

\(\overline{FG} = \frac{\overline{EF}}{\sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)

4° segmento (\(\overline{GH}\)):

H è il piede della perpendicolare da G al lato AB.

\(\overline{GH} = \frac{\overline{FG}}{\sqrt{2}} = \frac{\sqrt{2}/2}{\sqrt{2}} = \frac{1}{2}\)

Schema generale:

Osserviamo che ogni segmento è \(\frac{1}{\sqrt{2}}\) volte il precedente:

• \(a_1 = \overline{BE} = \sqrt{2}\)
• \(a_2 = \overline{EF} = \frac{\sqrt{2}}{\sqrt{2}} = 1\)
• \(a_3 = \overline{FG} = \frac{\sqrt{2}}{2}\)
• \(a_4 = \overline{GH} = \frac{\sqrt{2}}{4}\)

In generale: \(a_n = \sqrt{2} \cdot \left(\frac{1}{\sqrt{2}}\right)^{n-1} = \sqrt{2} \cdot \left(\frac{\sqrt{2}}{2}\right)^{n-1}\)

a) Somma dei primi n segmenti:

Abbiamo una progressione geometrica con primo termine \(a_1 = \sqrt{2}\) e ragione \(q = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\):

\[S_n = a_1 \cdot \frac{1-q^n}{1-q} = \sqrt{2} \cdot \frac{1-\left(\frac{\sqrt{2}}{2}\right)^n}{1-\frac{\sqrt{2}}{2}}\] \[S_n = \sqrt{2} \cdot \frac{1-\left(\frac{\sqrt{2}}{2}\right)^n}{\frac{2-\sqrt{2}}{2}} = \frac{2\sqrt{2}}{2-\sqrt{2}} \left(1-\left(\frac{\sqrt{2}}{2}\right)^n\right)\]

Razionalizzando il denominatore:

\[S_n = \frac{2\sqrt{2}(2+\sqrt{2})}{(2-\sqrt{2})(2+\sqrt{2})} \left(1-\left(\frac{\sqrt{2}}{2}\right)^n\right) = \frac{2\sqrt{2}(2+\sqrt{2})}{4-2} \left(1-\left(\frac{\sqrt{2}}{2}\right)^n\right)\] \[S_n = \sqrt{2}(2+\sqrt{2}) \left(1-\left(\frac{\sqrt{2}}{2}\right)^n\right) = (2\sqrt{2}+2) \left(1-\left(\frac{\sqrt{2}}{2}\right)^n\right)\]

b) Limite per n → ∞:

Poiché \(q = \frac{\sqrt{2}}{2} < 1\), la progressione geometrica, per \(n\) che tende all'infinito, tende a:

\[\lim_{n \to \infty} S_n = \frac{a_1}{1-q} = \frac{\sqrt{2}}{1-\frac{\sqrt{2}}{2}} = \frac{\sqrt{2}}{\frac{2-\sqrt{2}}{2}} = \frac{2\sqrt{2}}{2-\sqrt{2}}\]

Razionalizzando il denominatore:

\[\frac{2\sqrt{2}}{2-\sqrt{2}} \cdot \frac{2+\sqrt{2}}{2+\sqrt{2}} = \frac{2\sqrt{2}(2+\sqrt{2})}{4-2} = \frac{2\sqrt{2}(2+\sqrt{2})}{2} = \sqrt{2}(2+\sqrt{2}) = 2\sqrt{2}+2 = 2(\sqrt{2}+1)\]

Soluzioni finali:

a) \(\boxed{S_n = (2\sqrt{2}+2) \left(1-\left(\frac{\sqrt{2}}{2}\right)^n\right)}\)

b) \(\boxed{\lim_{n \to \infty} S_n = 2(\sqrt{2}+1)}\)

Soluzione Esercizio 4

Obiettivo: Trasformare \(f(x) = \sqrt{2}\sin(x) - \sqrt{2}\cos(x)\) nella forma \(A\sin(x + \alpha)\)

Passo 1: Raccogliere il fattore comune

\[f(x) = \sqrt{2}\sin(x) - \sqrt{2}\cos(x) = \sqrt{2}(\sin(x) - \cos(x))\]

Passo 2:

Utilizziamo la formula: \(a\sin(x) + b\cos(x) = \sqrt{a^2+b^2}\sin(x + \alpha)\) dove \(\tan(\alpha) = \frac{b}{a}\)

Nel nostro caso: \(a = 1\), \(b = -1\)

• \(\sqrt{a^2+b^2} = \sqrt{1^2+(-1)^2} = \sqrt{2}\)
• \(\tan(\alpha) = \frac{-1}{1} = -1 \Rightarrow \alpha = -\frac{\pi}{4}\)

Quindi: \(\sin(x) - \cos(x) = \sqrt{2}\sin\left(x - \frac{\pi}{4}\right)\)

Passo 3: Formula finale

\[f(x) = \sqrt{2} \cdot \sqrt{2}\sin\left(x - \frac{\pi}{4}\right) = 2\sin\left(x - \frac{\pi}{4}\right)\]

Costruzione del grafico per trasformazioni:

Partendo da \(y = \sin(x)\):

1. Traslazione orizzontale: \(y = \sin\left(x - \frac{\pi}{4}\right)\)
   Il grafico si sposta di \(\frac{\pi}{4}\) verso destra
   
2. Dilatazione verticale: \(y = 2\sin\left(x - \frac{\pi}{4}\right)\)
   Il grafico si dilata verticalmente con fattore 2 (ampiezza = 2)
   

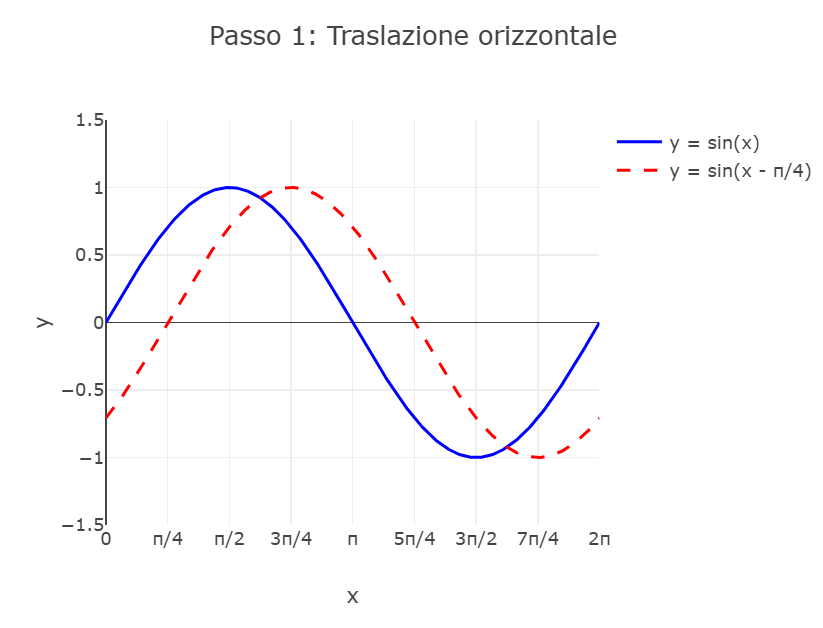
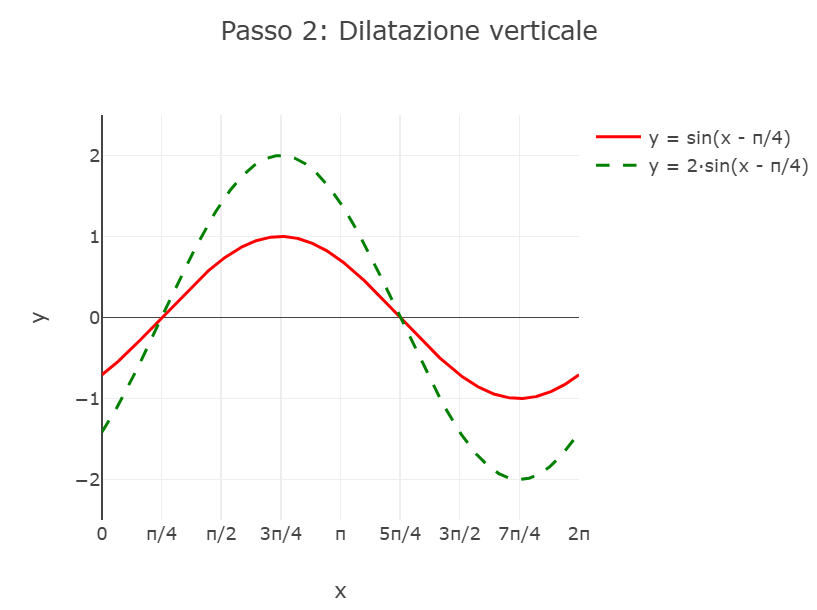
Caratteristiche del grafico finale:

• Ampiezza: \(A = 2\)
• Periodo: \(T = 2\pi\)
• Fase: \(\frac{\pi}{4}\) (spostamento a destra)

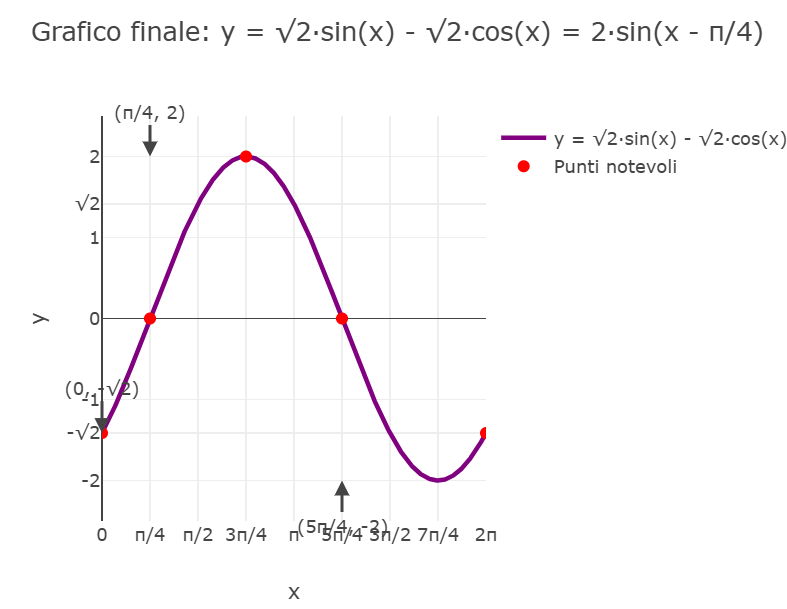
Punti notevoli nell'intervallo \([0, 2\pi]\):

• \(x = 0\): \(y = 2\sin\left(-\frac{\pi}{4}\right) = 2 \cdot \left(-\frac{\sqrt{2}}{2}\right) = -\sqrt{2}\)
• \(x = \frac{\pi}{4}\): \(y = 2\sin(0) = 0\)
• \(x = \frac{3\pi}{4}\): \(y = 2\sin\left(\frac{\pi}{2}\right) = 2\) (massimo)
• \(x = \frac{5\pi}{4}\): \(y = 2\sin(\pi) = 0\)
• \(x = \frac{7\pi}{4}\): \(y = 2\sin\left(\frac{3\pi}{2}\right) = -2\) (minimo)
• \(x = 2\pi\): \(y = 2\sin\left(\frac{7\pi}{4}\right) = 2 \cdot \left(-\frac{\sqrt{2}}{2}\right) = -\sqrt{2}\)

Conclusione:

Il grafico di \(f(x) = \sqrt{2}\sin(x) - \sqrt{2}\cos(x) = 2\sin\left(x - \frac{\pi}{4}\right)\) è una sinusoide con:

• Ampiezza 2 (oscillazione tra -2 e +2)
• Spostamento di fase di \(\frac{\pi}{4}\) verso destra rispetto a \(\sin(x)\)
• Stesso periodo di \(\sin(x)\), cioè \(2\pi\)