



Questo compito è stato assegnato nel mese di Ottobre del 1993 ad una classe 5ª del Liceo Scientifico.
Argomenti: Calcolo di limiti, Limiti in funzione di un parametro, grafico qualitativo di una funzione, proprietà dei limiti, grafico probabile di una funzione, problema con limiti.
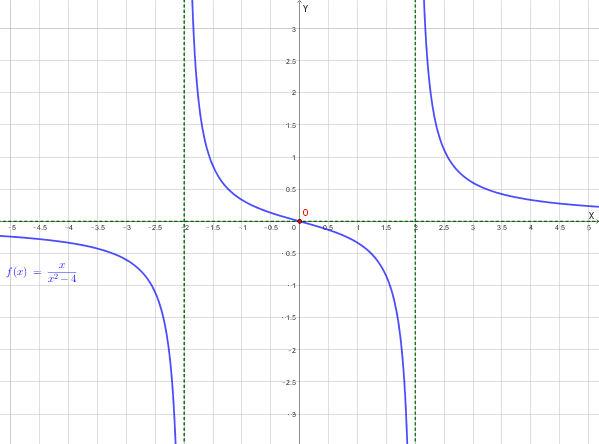
Tracciare un grafico qualitativo della seguente funzione:
\[ y = f(x) = \frac{x}{x^2-4} \]Sono richiesti:
1. Dominio:
Per determinare il dominio dobbiamo considerare che il denominatore deve essere diverso da zero:
\( x^2 - 4 \neq 0 \)
\( x^2 \neq 4 \)
\( x \neq \pm 2 \)
Dominio: \( D = \mathbb{R} \setminus \{-2, 2\} = (-\infty, -2) \cup (-2, 2) \cup (2, +\infty) \)
2. Parità e disparità:
Il dominio è simmetrico rispetto all'origine. Calcoliamo \( f(-x) \):
\[ f(-x) = \frac{-x}{(-x)^2-4} = \frac{-x}{x^2-4} = -\frac{x}{x^2-4} = -f(x) \]
Poiché \( f(-x) = -f(x) \), la funzione è dispari. Il grafico è quindi simmetrico rispetto all'origine.
3. Intersezioni con gli assi cartesiani:
4. Segno della funzione:
\[ f(x) = \frac{x}{x^2-4} = \frac{x}{(x-2)(x+2)} \]
Studiamo il segno dei fattori:
Studio del segno:
- Per \( x \in (-\infty, -2) \): \( \frac{(-)}{(-)(-)} = \frac{(-)}{(+)} < 0 \) → \( f(x) < 0 \)
- Per \( x \in (-2, 0) \): \( \frac{(-)}{(-)(+)} = \frac{(-)}{(-)} > 0 \) → \( f(x) > 0 \)
- Per \( x = 0 \): \( f(x) = 0 \)
- Per \( x \in (0, 2) \): \( \frac{(+)}{(-)(+)} = \frac{(+)}{(-)} < 0 \) → \( f(x) < 0 \)
- Per \( x \in (2, +\infty) \): \( \frac{(+)}{(+)(+)} = \frac{(+)}{(+)} > 0 \) → \( f(x) > 0 \)
Il grafico della funzione si trova nelle regioni chiare:

5. Limiti agli estremi del dominio:
Limiti per \( x \to -2 \):
\[ \lim_{x \to -2^-} f(x) = \lim_{x \to -2^-} \frac{x}{(x-2)(x+2)} = \frac{-2}{(-4) \cdot 0^-} = \frac{-2}{0^+} = -\infty \]
\[ \lim_{x \to -2^+} f(x) = \lim_{x \to -2^+} \frac{x}{(x-2)(x+2)} = \frac{-2}{(-4) \cdot 0^+} = \frac{-2}{0^-} = +\infty \]
Limiti per \( x \to 2 \):
\[ \lim_{x \to 2^-} f(x) = \lim_{x \to 2^-} \frac{x}{(x-2)(x+2)} = \frac{2}{0^- \cdot 4} = \frac{2}{0^-} = -\infty \]
\[ \lim_{x \to 2^+} f(x) = \lim_{x \to 2^+} \frac{x}{(x-2)(x+2)} = \frac{2}{0^+ \cdot 4} = \frac{2}{0^+} = +\infty \]
Limiti all'infinito:
\[ \lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \frac{x}{x^2-4} = \lim_{x \to -\infty} \frac{x}{x^2} = \lim_{x \to -\infty} \frac{1}{x} = 0 \]
\[ \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \frac{x}{x^2-4} = \lim_{x \to +\infty} \frac{1}{x} = 0 \]
6. Asintoti:
7. Intersezioni con gli asintoti:
Con l'asintoto orizzontale \( y = 0 \):
\( \frac{x}{x^2-4} = 0 \)
\( x = 0 \)
Intersezione nel punto \( (0, 0) \)
La funzione attraversa l'asintoto orizzontale nell'origine.
8. Grafico qualitativo:
Riassumendo le informazioni trovate:
Il grafico presenta tre rami separati:
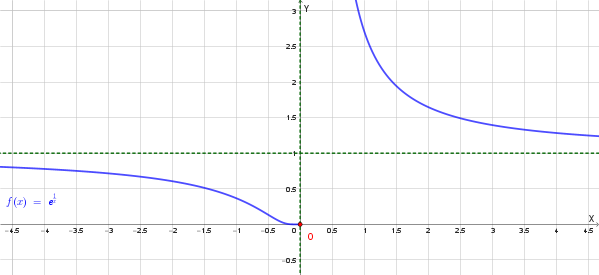
È data la seguente funzione:
\[ y = f(x) = e^{\frac{1}{x}} \]
a) Dominio, intersezioni, simmetrie e segno
Dominio:
La funzione \( f(x) = e^{\frac{1}{x}} \) è definita per tutti i valori di \( x \) tali che \( \frac{1}{x} \) esista, ovvero:
\( x \neq 0 \)
Dominio: \( D = \mathbb{R} \setminus \{0\} = (-\infty, 0) \cup (0, +\infty) \)
Intersezioni con gli assi:
Simmetrie:
Il dominio è simmetrico rispetto all'origine. Calcoliamo \( f(-x) \):
\[ f(-x) = e^{\frac{1}{-x}} = e^{-\frac{1}{x}} = \frac{1}{e^{\frac{1}{x}}} = \frac{1}{f(x)} \]
Poiché \( f(-x) \neq f(x) \) e \( f(-x) \neq -f(x) \), la funzione non è né pari né dispari.
Segno della funzione:
Poiché \( e^{\frac{1}{x}} > 0 \) per ogni \( x \in D \), la funzione è sempre positiva in tutto il suo dominio.
b) Regioni del piano in cui si trova il grafico
Poiché la funzione è sempre positiva (\( f(x) > 0 \)), il grafico si trova interamente nella regione del piano con \( y > 0 \) (sopra l'asse x).
Più precisamente:

c) Asintoto orizzontale \( y = 1 \)
Dobbiamo dimostrare che \( \lim_{x \to -\infty} f(x) = 1 \) e \( \lim_{x \to +\infty} f(x) = 1 \).
Per \( x \to +\infty \):
Quando \( x \to +\infty \), abbiamo \( \frac{1}{x} \to 0^+ \), quindi:
\[ \lim_{x \to +\infty} e^{\frac{1}{x}} = e^0 = 1 \]
Per \( x \to -\infty \):
Quando \( x \to -\infty \), abbiamo \( \frac{1}{x} \to 0^- \), quindi:
\[ \lim_{x \to -\infty} e^{\frac{1}{x}} = e^0 = 1 \]
Pertanto, \( y = 1 \) è asintoto orizzontale bilaterale per la funzione.
d) Limiti per \( x \to 0 \) con la definizione
Limite per \( x \to 0^+ \):
Dobbiamo dimostrare che \( \lim_{x \to 0^+} e^{\frac{1}{x}} = +\infty \).
Definizione: Per ogni \( M > 0 \), esiste \( \delta > 0 \) tale che se \( 0 < x < \delta \), allora \( f(x) > M \).
Dimostrazione:
Vogliamo che \( e^{\frac{1}{x}} > M \).
Applicando il logaritmo naturale (funzione crescente):
\[ \frac{1}{x} > \ln M \]
Poiché \( x > 0 \), moltiplicando per \( x \) (positivo) otteniamo:
\[ 1 > x \ln M \]
\[ x < \frac{1}{\ln M} \]
Se \( M > 1 \), allora \( \ln M > 0 \) e possiamo scegliere \( \delta = \frac{1}{\ln M} \).
Quindi, per ogni \( M > 1 \), se \( 0 < x < \delta = \frac{1}{\ln M} \), allora \( f(x) > M \).
Limite per \( x \to 0^- \):
Dobbiamo dimostrare che \( \lim_{x \to 0^-} e^{\frac{1}{x}} = 0 \).
Definizione: Per ogni \( \varepsilon > 0 \), esiste \( \delta > 0 \) tale che se \( -\delta < x < 0 \), allora \( |f(x) - 0| < \varepsilon \), cioè \( f(x) < \varepsilon \).
Dimostrazione:
Vogliamo che \( e^{\frac{1}{x}} < \varepsilon \).
Applicando il logaritmo naturale:
\[ \frac{1}{x} < \ln \varepsilon \]
Poiché \( 0 < \varepsilon < 1 \), abbiamo \( \ln \varepsilon < 0 \).
Per \( x < 0 \), moltiplicando per \( x \) (negativo) si inverte la disuguaglianza:
\[ 1 > x \ln \varepsilon \]
\[ x > \frac{1}{\ln \varepsilon} \]
Possiamo scegliere \( \delta = -\frac{1}{\ln \varepsilon} > 0 \) (poiché \( \ln \varepsilon < 0 \)).
Quindi, per ogni \( \varepsilon \in (0, 1) \), se \( -\delta < x < 0 \), allora \( f(x) < \varepsilon \).
e) Monotonia della funzione
Dobbiamo dimostrare che la funzione è decrescente in tutto il suo dominio.
Definizione: Una funzione è decrescente in un intervallo se per ogni \( x_1, x_2 \) nell'intervallo con \( x_1 < x_2 \), si ha \( f(x_1) > f(x_2) \).
Dimostrazione:
Consideriamo due casi:
Caso 1: \( x_1, x_2 > 0 \) con \( x_1 < x_2 \)
Poiché \( x_1 < x_2 \), abbiamo \( \frac{1}{x_1} > \frac{1}{x_2} \) (la funzione \( \frac{1}{x} \) è decrescente per \( x > 0 \)).
Poiché la funzione esponenziale è crescente:
\[ e^{\frac{1}{x_1}} > e^{\frac{1}{x_2}} \]
Quindi \( f(x_1) > f(x_2) \).
Caso 2: \( x_1, x_2 < 0 \) con \( x_1 < x_2 \)
Poiché \( x_1 < x_2 < 0 \), abbiamo \( \frac{1}{x_1} > \frac{1}{x_2} \) (la funzione \( \frac{1}{x} \) è decrescente anche per \( x < 0 \)).
Di nuovo, per la crescenza dell'esponenziale:
\[ e^{\frac{1}{x_1}} > e^{\frac{1}{x_2}} \]
Quindi \( f(x_1) > f(x_2) \).
Conclusione: La funzione \( f(x) = e^{\frac{1}{x}} \) è decrescente in ciascuno degli intervalli \( (-\infty, 0) \) e \( (0, +\infty) \) che costituiscono il suo dominio.
f) Asintoti della funzione
g) Grafico probabile
Riassumendo le informazioni:
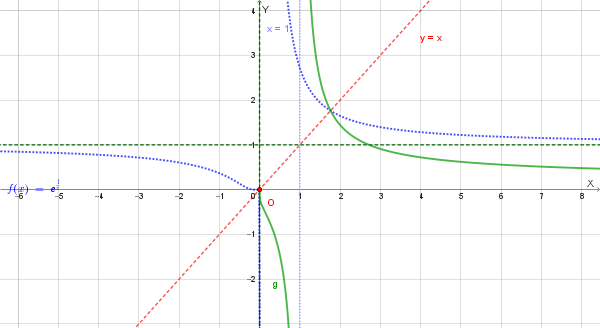
h) Funzione inversa
Invertibilità:
La funzione \( f(x) = e^{\frac{1}{x}} \) è strettamente decrescente in ciascun ramo del suo dominio, quindi è iniettiva. Inoltre, essendo continua e assumendo tutti i valori positivi, è anche suriettiva su \( (0, +\infty) \) in ciascun ramo. Pertanto, la funzione è invertibile.
Determinazione della funzione inversa:
Partiamo dall'equazione \( y = e^{\frac{1}{x}} \) e risolviamo rispetto a \( x \):
\[ y = e^{\frac{1}{x}} \]
Applicando il logaritmo naturale:
\[ \ln y = \frac{1}{x} \]
Quindi:
\[ x = \frac{1}{\ln y} \]
Scambiando \( x \) e \( y \), otteniamo la funzione inversa:
\[ y = g(x) = \frac{1}{\ln x} \]
con dominio \( x > 0 \) e \( x \neq 1 \), cioè \( D_g = (0, 1) \cup (1, +\infty) \).
Grafico della funzione inversa:
Il grafico di \( g(x) = \frac{1}{\ln x} \) si ottiene per simmetria rispetto alla bisettrice del primo e terzo quadrante (\( y = x \)) a partire dal grafico di \( f(x) \).
Proprietà di \( g(x) \):
Calcolare i seguenti limiti:
a) \(\displaystyle\lim_{x \to 1^+} \frac{x^2-7x+6}{x-1}\)
Calcoliamo prima il valore del numeratore per \(x = 1\):
\(1^2 - 7(1) + 6 = 1 - 7 + 6 = 0\)
Poiché sia il numeratore che il denominatore si annullano per \(x = 1\), abbiamo una forma indeterminata \(\frac{0}{0}\). Fattorizziamo il numeratore:
\(x^2 - 7x + 6 = (x-1)(x-6)\)
Il limite diventa:
\[ \lim_{x \to 1^+} \frac{(x-1)(x-6)}{x-1} = \lim_{x \to 1^+} (x-6) = 1-6 = -5 \]
Risposta: \(-5\)
b) \(\displaystyle\lim_{x \to +\infty} \frac{2x^2+x-1}{3x^2+1}\)
Si tratta di un limite di funzione razionale con numeratore e denominatore dello stesso grado (entrambi di secondo grado).
Dividiamo numeratore e denominatore per \(x^2\):
\[ \lim_{x \to +\infty} \frac{2x^2+x-1}{3x^2+1} = \lim_{x \to +\infty} \frac{2+\frac{1}{x}-\frac{1}{x^2}}{3+\frac{1}{x^2}} \]
Per \(x \to +\infty\), i termini \(\frac{1}{x}\), \(\frac{1}{x^2}\) tendono a zero:
\[ = \frac{2+0-0}{3+0} = \frac{2}{3} \]
Risposta: \(\frac{2}{3}\)
c) \(\displaystyle\lim_{x \to -\infty} \frac{x^3-1}{2x^2+3}\)
Il grado del numeratore (3) è maggiore del grado del denominatore (2), quindi il limite sarà infinito.
Dividiamo numeratore e denominatore per \(x^2\):
\[ \lim_{x \to -\infty} \frac{x^3-1}{2x^2+3} = \lim_{x \to -\infty} \frac{x-\frac{1}{x^2}}{2+\frac{3}{x^2}} \]
Per \(x \to -\infty\):
Quindi: \[ \lim_{x \to -\infty} \frac{x-\frac{1}{x^2}}{2+\frac{3}{x^2}} = \frac{-\infty}{2} = -\infty \] Risposta: \(-\infty\)
d) \(\displaystyle\lim_{x \to +\infty} \frac{x^2+x+1}{2x^3+5}\)
Il grado del numeratore (2) è minore del grado del denominatore (3), quindi il limite è zero.
Dividiamo numeratore e denominatore per \(x^3\):
\[ \lim_{x \to +\infty} \frac{x^2+x+1}{2x^3+5} = \lim_{x \to +\infty} \frac{\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x^3}}{2+\frac{5}{x^3}} \]
Per \(x \to +\infty\), tutti i termini con potenze negative di \(x\) tendono a zero:
\[ = \frac{0+0+0}{2+0} = \frac{0}{2} = 0 \]
Risposta: \(0\)
e) \(\displaystyle\lim_{x \to 2} \frac{x^3-x^2-x-2}{x^2-8}\)
Calcoliamo i valori per \(x = 2\):
Numeratore: \(2^3 - 2^2 - 2 - 2 = 8 - 4 - 2 - 2 = 0\)
Denominatore: \(2^2 - 8 = 4 - 8 = -4 \neq 0\)
Poiché solo il numeratore si annulla, il limite è:
\[ \lim_{x \to 2} \frac{x^3-x^2-x-2}{x^2-8} = \frac{0}{-4} = 0 \]
Risposta: \(0\)
f) \(\displaystyle\lim_{x \to -\infty} \frac{\sqrt{4x^2+1}-\sqrt{x^2-1}}{|x|+1}\)
Per \(x \to -\infty\), abbiamo \(x < 0\), quindi \(|x| = -x\).
Inoltre, per \(x < 0\):
\[ \sqrt{x^2} = |x| = -x \]
Riscriviamo le radici estraendo \(x^2\):
\[ \sqrt{4x^2+1} = |x|\sqrt{4+\frac{1}{x^2}} = -x\sqrt{4+\frac{1}{x^2}} \]
\[ \sqrt{x^2-1} = |x|\sqrt{1-\frac{1}{x^2}} = -x\sqrt{1-\frac{1}{x^2}} \]
Il limite diventa:
\[ \lim_{x \to -\infty} \frac{-x\sqrt{4+\frac{1}{x^2}} - (-x)\sqrt{1-\frac{1}{x^2}}}{-x+1} = \lim_{x \to -\infty} \frac{-x\left(\sqrt{4+\frac{1}{x^2}} - \sqrt{1-\frac{1}{x^2}}\right)}{-x+1} \]
Dividiamo numeratore e denominatore per \(-x\):
\[ = \lim_{x \to -\infty} \frac{\sqrt{4+\frac{1}{x^2}} - \sqrt{1-\frac{1}{x^2}}}{1-\frac{1}{x}} \]
Per \(x \to -\infty\):
\[ = \frac{\sqrt{4+0} - \sqrt{1-0}}{1-0} = \frac{2-1}{1} = 1 \]
Risposta: \(1\)
g) \(\displaystyle\lim_{x \to 0^-} e^{\frac{x^2-x}{x^3+x}}\)
Semplifichiamo prima l'esponente:
\[ \frac{x^2-x}{x^3+x} = \frac{x(x-1)}{x(x^2+1)} = \frac{x-1}{x^2+1} \]
Calcoliamo il limite dell'esponente per \(x \to 0^-\):
\[ \lim_{x \to 0^-} \frac{x-1}{x^2+1} = \frac{0-1}{0+1} = \frac{-1}{1} = -1 \]
Poiché la funzione esponenziale è continua:
\[ \lim_{x \to 0^-} e^{\frac{x^2-x}{x^3+x}} = e^{-1} = \frac{1}{e} \]
Risposta: \(\frac{1}{e}\)
h) \(\displaystyle\lim_{x \to 0^+} \ln\left(1+\frac{1}{\sin(x)}\right)\)
Per \(x \to 0^+\), abbiamo \(\sin(x) \to 0^+\) (poiché \(\sin(x) > 0\) per \(x\) piccolo e positivo).
Quindi:
\[ \frac{1}{\sin(x)} \to +\infty \]
\[ 1 + \frac{1}{\sin(x)} \to +\infty \]
Poiché il logaritmo naturale tende a \(+\infty\) quando l'argomento tende a \(+\infty\):
\[ \lim_{x \to 0^+} \ln\left(1+\frac{1}{\sin(x)}\right) = +\infty \]
Risposta: \(+\infty\)
i) \(\displaystyle\lim_{x \to +\infty} \left(\sqrt{3x-1}-a\sqrt{x}\right)\) al variare di \(a \in \mathbb{R}\)
Riscriviamo estraendo \(\sqrt{x}\):
\[ \sqrt{3x-1} - a\sqrt{x} = \sqrt{x}\left(\sqrt{3-\frac{1}{x}} - a\right) \]
Per \(x \to +\infty\):
\[ \sqrt{3-\frac{1}{x}} \to \sqrt{3} \]
Quindi:
\[ \lim_{x \to +\infty} \sqrt{x}\left(\sqrt{3-\frac{1}{x}} - a\right) = \lim_{x \to +\infty} \sqrt{x} \cdot (\sqrt{3} - a) \]
Analisi al variare di \(a\):
Per il caso \(a = \sqrt{3}\), analizziamo meglio razionalizzando:
\[ \sqrt{3x-1} - \sqrt{3}\sqrt{x} = \frac{(\sqrt{3x-1})^2 - (\sqrt{3}\sqrt{x})^2}{\sqrt{3x-1} + \sqrt{3}\sqrt{x}} = \frac{3x-1-3x}{\sqrt{3x-1} + \sqrt{3}\sqrt{x}} = \frac{-1}{\sqrt{3x-1} + \sqrt{3}\sqrt{x}} \]
Per \(x \to +\infty\), il denominatore tende a \(+\infty\), quindi il limite è \(0\).
Risposta:
\[
\lim_{x \to +\infty} \left(\sqrt{3x-1}-a\sqrt{x}\right) =
\begin{cases}
+\infty & \text{se } a < \sqrt{3} \\
0 & \text{se } a = \sqrt{3} \\
-\infty & \text{se } a > \sqrt{3}
\end{cases}
\]
l) \(\displaystyle\lim_{x \to -\infty} 2^{\frac{ax^2+x+1}{3x^2-1}}\) al variare di \(a \in \mathbb{R}\)
Calcoliamo prima il limite dell'esponente dividendo numeratore e denominatore per \(x^2\):
\[ \lim_{x \to -\infty} \frac{ax^2+x+1}{3x^2-1} = \lim_{x \to -\infty} \frac{a+\frac{1}{x}+\frac{1}{x^2}}{3-\frac{1}{x^2}} \]
Per \(x \to -\infty\):
\[ = \frac{a+0+0}{3-0} = \frac{a}{3} \]
Quindi:
\[ \lim_{x \to -\infty} 2^{\frac{ax^2+x+1}{3x^2-1}} = 2^{\frac{a}{3}} \]
Risposta: Il limite è \(2^{\frac{a}{3}}\) per ogni \(a \in \mathbb{R}\).
Casi particolari:
La semiretta AR divide l'angolo \(\widehat{MAN} < \frac{\pi}{2}\) in due angoli \(\widehat{NAR}\) e \(\widehat{MAR}\) tali che \(\widehat{NAR} = 2\widehat{MAR}\).
Condurre per il punto P della semiretta AR, tale che sia \(AP = 1\), una retta che incontri la semiretta AM in B e la semiretta AN in C e tale che sia \(\widehat{PBA} = \widehat{NAR}\).
Determinare le aree \(A_1\) e \(A_2\) dei triangoli PAB e PAC e calcolare il limite del rapporto fra \(A_1\) e \(A_2\) quando l'angolo \(\widehat{MAR}\) tende a 0.
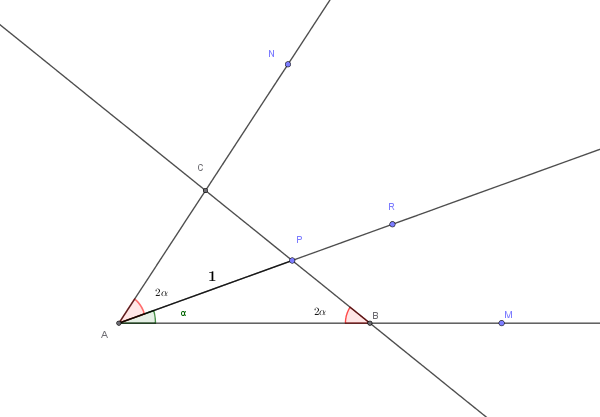
Impostazione del problema
Poniamo \(\widehat{MAR} = \alpha\), quindi \(\widehat{NAR} = 2\alpha\) e di conseguenza:
\[ \widehat{MAN} = \widehat{MAR} + \widehat{NAR} = \alpha + 2\alpha = 3\alpha \]
La condizione \(\widehat{MAN} < \frac{\pi}{2}\) implica che \(3\alpha < \frac{\pi}{2}\), ovvero \(\alpha < \frac{\pi}{6}\).
Dato che \(AP = 1\) e \(\widehat{PBA} = \widehat{NAR} = 2\alpha\), studiamo la configurazione geometrica.
Analisi del triangolo PAB
Nel triangolo PAB abbiamo:
Applicando il teorema dei seni nel triangolo PAB con \(AP = 1\): \[ \frac{AP}{\sin(\widehat{PBA})} = \frac{PB}{\sin(\widehat{PAB})} = \frac{AB}{\sin(\widehat{APB})} \] \[ \frac{1}{\sin(2\alpha)} = \frac{PB}{\sin(\alpha)} = \frac{AB}{\sin(\pi - 3\alpha)} \] Da cui: \[ PB = \frac{\sin(\alpha)}{\sin(2\alpha)} = \frac{\sin(\alpha)}{2\sin(\alpha)\cos(\alpha)} = \frac{1}{2\cos(\alpha)} \] \[ AB = \frac{\sin(3\alpha)}{\sin(2\alpha)} \]
Area del triangolo PAB
L'area si calcola con la formula:
\[ A_1 = \frac{1}{2} \cdot AP \cdot PB \cdot \sin(\widehat{APB}) = \frac{1}{2} \cdot 1 \cdot \frac{1}{2\cos(\alpha)} \cdot \sin(3\alpha) \]
\[ A_1 = \frac{\sin(3\alpha)}{4\cos(\alpha)} \]
Analisi del triangolo ABC
Nel triangolo ABC abbiamo:
Poiché P appartiene al segmento BC, il triangolo PAC è formato da A, P e C.
Analisi del triangolo PAC
Nel triangolo PAC abbiamo:
Applicando il teorema dei seni nel triangolo PAC: \[ \frac{AP}{\sin(\widehat{PCA})} = \frac{PC}{\sin(\widehat{PAC})} \] \[ \frac{1}{\sin(\pi - 5\alpha)} = \frac{PC}{\sin(2\alpha)} \] \[ PC = \frac{\sin(2\alpha)}{\sin(5\alpha)} \]
Area del triangolo PAC
\[ A_2 = \frac{1}{2} \cdot AP \cdot PC \cdot \sin(\widehat{APC}) = \frac{1}{2} \cdot 1 \cdot \frac{\sin(2\alpha)}{\sin(5\alpha)} \cdot \sin(3\alpha) \]
\[ A_2 = \frac{\sin(2\alpha) \cdot \sin(3\alpha)}{2\sin(5\alpha)} \]
Rapporto delle aree
\[ \frac{A_1}{A_2} = \frac{\frac{\sin(3\alpha)}{4\cos(\alpha)}}{\frac{\sin(2\alpha) \cdot \sin(3\alpha)}{2\sin(5\alpha)}} = \frac{\sin(3\alpha)}{4\cos(\alpha)} \cdot \frac{2\sin(5\alpha)}{\sin(2\alpha) \cdot \sin(3\alpha)} \]
\[ = \frac{2\sin(5\alpha)}{4\cos(\alpha) \cdot \sin(2\alpha)} = \frac{\sin(5\alpha)}{2\cos(\alpha) \cdot \sin(2\alpha)} \]
Calcolo del limite
Dobbiamo calcolare:
\[ \lim_{\alpha \to 0} \frac{\sin(5\alpha)}{2\cos(\alpha) \cdot \sin(2\alpha)} \]
Usando il limite notevole \(\lim_{x \to 0} \frac{\sin(x)}{x} = 1\), riscriviamo:
\[ \lim_{\alpha \to 0} \frac{\sin(5\alpha)}{2\cos(\alpha) \cdot \sin(2\alpha)} = \lim_{\alpha \to 0} \frac{5\alpha \cdot \frac{\sin(5\alpha)}{5\alpha}}{2\cos(\alpha) \cdot 2\alpha \cdot \frac{\sin(2\alpha)}{2\alpha}} \]
\[ = \lim_{\alpha \to 0} \frac{5\alpha}{2\cos(\alpha) \cdot 2\alpha} \cdot \frac{\frac{\sin(5\alpha)}{5\alpha}}{\frac{\sin(2\alpha)}{2\alpha}} \]
\[ = \lim_{\alpha \to 0} \frac{5}{4\cos(\alpha)} \cdot \frac{1}{1} = \frac{5}{4 \cdot 1} = \frac{5}{4} \]
Risposta:
Le aree dei triangoli sono:
\[ A_1 = \frac{\sin(3\alpha)}{4\cos(\alpha)} \]
\[ A_2 = \frac{\sin(2\alpha) \cdot \sin(3\alpha)}{2\sin(5\alpha)} \]
Il limite del rapporto quando \(\alpha \to 0\) è:
\[ \boxed{\lim_{\alpha \to 0} \frac{A_1}{A_2} = \frac{5}{4}} \]
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.