



Questo compito è stato assegnato il giorno 17 Novembre 1994 a una classe 5ª del Liceo Scientifico.
Argomenti: Dimostrazione limiti con la definizione, Calcolo di limiti, Problema di trigonometria con calcolo di limite.
Servendosi della definizione dimostrare che:
a) \(\lim_{x \to 1^+} \frac{x^2-7x+6}{x-1} = -5\)
b) \(\lim_{x \to 0} \frac{2x-5}{x^2} = -\infty\)
Prima semplifichiamo l'espressione:
Fattorizziamo il numeratore: \(x^2-7x+6 = (x-1)(x-6)\)
Quindi: \(\frac{x^2-7x+6}{x-1} = \frac{(x-1)(x-6)}{x-1} = x-6\) per \(x \neq 1\)
Dimostrazione con la definizione:
Dobbiamo dimostrare che per ogni \(\varepsilon > 0\), esiste \(\delta > 0\) tale che:
se \(1 < x < 1 + \delta\), allora \(|(x-6) - (-5)| < \varepsilon\)
Semplifichiamo: \(|(x-6) - (-5)| = |x-6+5| = |x-1|\)
Vogliamo quindi: se \(1 < x < 1 + \delta\), allora \(|x-1| < \varepsilon\)
Poiché \(x > 1\), abbiamo \(|x-1| = x-1\)
La condizione diventa: se \(1 < x < 1 + \delta\), allora \(x-1 < \varepsilon\)
Questo è soddisfatto scegliendo \(\delta = \varepsilon\)
Conclusione: Per ogni \(\varepsilon > 0\), posto \(\delta = \varepsilon\), si ha che per \(1 < x < 1 + \delta\): \(|(x-6) - (-5)| = |x-1| = x-1 < \delta = \varepsilon\)
Dimostrazione con la definizione di limite infinito:
Dobbiamo dimostrare che per ogni \(M > 0\) esiste un intorno \(I\) di 0 tale che, per ogni \(x \in I\) (al più 0 escluso) risulta:
\(\frac{2x-5}{x^2} < -M\)
Risoluzione della disequazione:
La disequazione \(\frac{2x-5}{x^2} < -M\) equivale a:
\(\frac{2x-5}{x^2} + M < 0\)
\(\frac{2x-5+Mx^2}{x^2} < 0\)
Poiché \(x^2 > 0\) per \(x \neq 0\), la disequazione è equivalente a:
\(2x-5+Mx^2 < 0\)
\(Mx^2 + 2x - 5 < 0\)
<Risoluzione della disequazione di secondo grado:
Consideriamo l'equazione \(Mx^2 + 2x - 5 = 0\)
Discriminante: \(\Delta = 4 + 4 \cdot 5M = 4 + 20M > 0\) (sempre positivo)
Le soluzioni sono:
\(x_{1,2} = \frac{-2 \pm \sqrt{4 + 20M}}{2M} = \frac{-1 \pm \sqrt{1 + 5M}}{M}\)
Quindi:
\(x_1 = \frac{-1 - \sqrt{1 + 5M}}{M} < 0\)
\(x_2 = \frac{-1 + \sqrt{1 + 5M}}{M} > 0\)
Poiché il coefficiente di \(x^2\) è positivo (\(M > 0\)) la disequazione \(Mx^2 + 2x - 5 < 0\) è soddisfatta per:
\(x_1 < x < x_2\)
Ovvero: \(\frac{-1 - \sqrt{1 + 5M}}{M} < x < \frac{-1 + \sqrt{1 + 5M}}{M}\)
Conclusione:
L'intervallo \(\left(\frac{-1 - \sqrt{1 + 5M}}{M}, \frac{-1 + \sqrt{1 + 5M}}{M}\right)\) contiene 0 ed è quindi un intorno di 0, come volevamo dimostrare.
Calcolare i seguenti limiti:
a) \(\lim_{x \to 2} \frac{3-\sqrt{5x-1}}{4-x^2}\)
b) \(\lim_{x \to +\infty} \left(\sqrt{x^2+x}-\sqrt{x}\right)\)
c) \(\lim_{x \to 1} \frac{x^2+|x-1|-1}{x-1}\)
Verifichiamo la forma indeterminata:
Per \(x \to 2\): numeratore \(\to 3-\sqrt{9} = 3-3 = 0\)
Per \(x \to 2\): denominatore \(\to 4-4 = 0\)
Abbiamo la forma indeterminata \(\frac{0}{0}\)
Razionalizziamo il numeratore:
Moltiplichiamo per \(\frac{3+\sqrt{5x-1}}{3+\sqrt{5x-1}}\):
\(\frac{3-\sqrt{5x-1}}{4-x^2} \cdot \frac{3+\sqrt{5x-1}}{3+\sqrt{5x-1}} = \frac{9-(5x-1)}{(4-x^2)(3+\sqrt{5x-1})} = \frac{10-5x}{(4-x^2)(3+\sqrt{5x-1})}\)
Fattorizziamo:
\(10-5x = -5(x-2)\) e \(4-x^2 = -(x^2-4) = -(x-2)(x+2)\)
Quindi: \(\frac{-5(x-2)}{-(x-2)(x+2)(3+\sqrt{5x-1})} = \frac{5}{(x+2)(3+\sqrt{5x-1})}\)
Calcolo del limite:
\(\lim_{x \to 2} \frac{5}{(x+2)(3+\sqrt{5x-1})} = \frac{5}{(2+2)(3+\sqrt{9})} = \frac{5}{4 \cdot 6} = \frac{5}{24}\)
Forma indeterminata \(\infty - \infty\):
Razionalizziamo moltiplicando per \(\frac{\sqrt{x^2+x}+\sqrt{x}}{\sqrt{x^2+x}+\sqrt{x}}\):
\(\frac{(\sqrt{x^2+x})^2 - (\sqrt{x})^2}{\sqrt{x^2+x}+\sqrt{x}} = \frac{x^2+x-x}{\sqrt{x^2+x}+\sqrt{x}} = \frac{x^2}{\sqrt{x^2+x}+\sqrt{x}}\)
Semplificazione per \(x > 0\):
Dividiamo numeratore e denominatore per \(x\):
\(\frac{x^2}{\sqrt{x^2+x}+\sqrt{x}} = \frac{x}{\frac{\sqrt{x^2+x}+\sqrt{x}}{x}} = \frac{x}{\frac{\sqrt{x^2+x}}{x}+\frac{\sqrt{x}}{x}}\)
Per \(x > 0\): \(\frac{\sqrt{x^2+x}}{x} = \sqrt{\frac{x^2+x}{x^2}} = \sqrt{1+\frac{1}{x}}\) e \(\frac{\sqrt{x}}{x} = \frac{1}{\sqrt{x}}\)
Calcolo del limite:
Per \(x \to +\infty\): \(\sqrt{1+\frac{1}{x}} \to 1\) e \(\frac{1}{\sqrt{x}} \to 0\)
Quindi: \(\lim_{x \to +\infty} \frac{x}{1+0} = \lim_{x \to +\infty} x = +\infty\)
Studio del valore assoluto:
Dobbiamo distinguere i casi in base al segno di \(x-1\):
Caso 1: \(x > 1\) (limite destro)
Per \(x > 1\): \(|x-1| = x-1\)
\(\frac{x^2+(x-1)-1}{x-1} = \frac{x^2+x-2}{x-1}\)
Fattorizziamo: \(x^2+x-2 = (x-1)(x+2)\)
Quindi: \(\frac{(x-1)(x+2)}{x-1} = x+2\)
\(\lim_{x \to 1^+} (x+2) = 1+2 = 3\)
Caso 2: \(x < 1\) (limite sinistro)
Per \(x < 1\): \(|x-1| = -(x-1) = 1-x\)
\(\frac{x^2+(1-x)-1}{x-1} = \frac{x^2-x}{x-1} = \frac{x(x-1)}{x-1} = x\)
\(\lim_{x \to 1^-} x = 1\)
Conclusione:
Poiché \(\lim_{x \to 1^+} = 3 \neq 1 = \lim_{x \to 1^-}\), il limite non esiste.
Risolvere i seguenti limiti:
a) \(\lim_{x \to \infty} \frac{\sqrt{x^2+x}}{x-1}\)
b) \(\lim_{x \to \left(\frac{\pi}{6}\right)^+} \left(\frac{1}{2}\right)^{\frac{1}{1-2\sin(x)}}\)
Analisi del comportamento:
Per \(x \to \infty\): numeratore \(\to +\infty\) e denominatore \(\to +\infty\)
Abbiamo la forma indeterminata \(\frac{\infty}{\infty}\)
Semplificazione del numeratore:
Per \(x > 0\): \(\sqrt{x^2+x} = \sqrt{x^2(1+\frac{1}{x})} = x\sqrt{1+\frac{1}{x}}\)
Il limite diventa:
\(\lim_{x \to \infty} \frac{x\sqrt{1+\frac{1}{x}}}{x-1}\)
Dividiamo numeratore e denominatore per \(x\):
\(\lim_{x \to \infty} \frac{\sqrt{1+\frac{1}{x}}}{1-\frac{1}{x}}\)
Calcolo del limite:
Per \(x \to \infty\): \(\sqrt{1+\frac{1}{x}} \to \sqrt{1+0} = 1\) e \(1-\frac{1}{x} \to 1-0 = 1\)
Quindi: \(\lim_{x \to \infty} \frac{\sqrt{x^2+x}}{x-1} = \frac{1}{1} = 1\)
Analisi del comportamento dell'esponente:
Per \(x \to \left(\frac{\pi}{6}\right)^+\): \(\sin(x) \to \sin\left(\frac{\pi}{6}\right)^+ = (\frac{1}{2})^+\)
Quindi: \(1-2\sin(x) \to 1-2 \cdot \left(\frac{1}{2}\right)^+ = 0^-\) (da sinistra)
Eventuale forma indeterminata:
Abbiamo la forma \(\left(\frac{1}{2}\right)^{-\infty}\)
Poiché \(0 < \frac{1}{2} < 1\), quando l'esponente tende a \(-\infty\), la base elevata a potenza negativa molto grande tende a \(+\infty\)
Conclusione:
\(\lim_{x \to \left(\frac{\pi}{6}\right)^+} \left(\frac{1}{2}\right)^{\frac{1}{1-2\sin(x)}} = +\infty\)
In una circonferenza di raggio \(R\) è condotta una corda \(AB\) di misura \(R\sqrt{3}\). Sul maggiore dei due archi \(AB\) si prenda un punto \(D\) e sia \(AC\) la bisettrice dell'angolo \(BAD\).
Indicata con \(x\) la misura dell'angolo \(BAC\), calcolare:
\(\lim_{D \to B} \frac{\overline{BD} \cdot \overline{AC}}{\overline{BC} \cdot \overline{AD}}\)
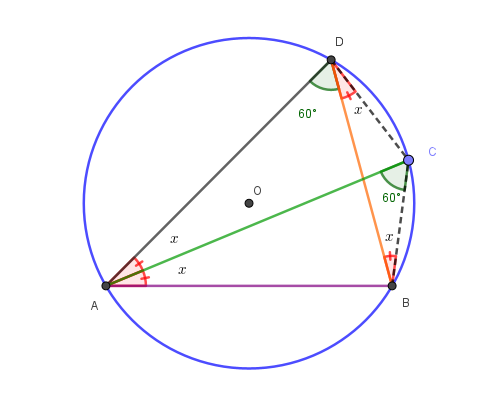
Analisi della configurazione geometrica:
Per una nota proprietà geometrica, \(AB\) è il lato del triangolo equilatero inscritto nella circonferenza, quindi l'angolo \(A\hat{D}B = 60°\).
Allo stesso risultato si può arrivare applicando il teorema della corda: \(AB = 2R\sin(A\hat{D}B)\), da cui:
\(R\sqrt{3} = 2R\sin(A\hat{D}B)\)
\(\sin(A\hat{D}B) = \frac{\sqrt{3}}{2}\), quindi \(A\hat{D}B = 60°\)
Proprietà degli angoli alla circonferenza:
• L'angolo \(A\hat{C}B = 60°\) perché insiste sullo stesso arco \(AB\) su cui insiste \(A\hat{D}B\).
• L'angolo \(B\hat{D}C = x\) perché insiste sullo stesso arco \(BC\) su cui insiste l'angolo \(B\hat{A}C\).
• L'angolo \(D\hat{B}C = x\) perché insiste sullo stesso arco \(CD\) su cui insiste l'angolo \(D\hat{A}C\).
Comportamento al limite:
Osserviamo che se \(D \to B\) \(2x \to 0\), allora \(x \to 0\) e inoltre:
• \(AC \to AB\)
• \(AD \to AB\)
Quindi nel limite richiesto possiamo semplificare \(AC\) con \(AD\) ed il limite diventa:
\(\lim_{x \to 0} \frac{BD}{BC}\)
Applicazione del Teorema della corda:
Cerchiamo \(BD\) e \(BC\):
• \(BD = 2R\sin(2x)\)
• \(BC = 2R\sin(x)\)
Calcolo del limite:
Il limite diventa quindi:
\(\lim_{x \to 0} \frac{2R\sin(2x)}{2R\sin(x)} = \lim_{x \to 0} \frac{\sin(2x)}{\sin(x)}\)
Usando la formula \(\sin(2x) = 2\sin(x)\cos(x)\):
\(\lim_{x \to 0} \frac{2\sin(x)\cos(x)}{\sin(x)} = \lim_{x \to 0} 2\cos(x) = 2\cos(0) = 2\)
Conclusione:
\(\lim_{D \to B} \frac{\overline{BD} \cdot \overline{AC}}{\overline{BC} \cdot \overline{AD}} = 2\)
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.