



Questo compito è stato assegnato il 18 Dicembre 2003 a una classe 5ª del Liceo Scientifico.
Argomenti: Funzione razionale fratta con parametri, studio di funzione razionale fratta,
Angolo sotto cui si tagliano due curve, Cubica dipendente da un parametro, Angolo fra due rette, Soluzione approssimata di un'equazione di terzo grado, Parabola per tre punti, Area segmento parabolico, Teorema di Archimede.
a) Determinare \(a\) e \(b\) in modo che la funzione di equazione
\[ y = f(x) = \frac{ax + b}{x^2} \]
passi per il punto \(A = (1, 3)\) e abbia ivi per tangente la retta \(r\) di equazione \(4x + y - 7 = 0\).
b) Fai uno studio dettagliato della funzione ottenuta e rappresentala graficamente nel piano cartesiano.
La funzione da considerare è \(f(x) = \frac{ax + b}{x^2}\).
Abbiamo due condizioni da imporre:
1. Condizione di Passaggio: \(f(1) = 3\)
\[ f(1) = \frac{a(1) + b}{1^2} = a + b \]
Quindi:
\[ a + b = 3 \quad \text{...(Eq. I)} \]
2. Condizione di Tangenza: \(f'(1) = m_r\)
Prima calcoliamo il coefficiente angolare \(m_r\) della retta \(r: 4x + y - 7 = 0\):
\[ y = -4x + 7 \quad \Rightarrow \quad m_r = -4 \]
Ora calcoliamo la derivata prima \(f'(x)\) (regola del quoziente):
\[ f'(x) = \frac{a \cdot x^2 - (ax + b) \cdot 2x}{(x^2)^2} = \frac{ax^2 - 2ax^2 - 2bx}{x^4} = \frac{-ax^2 - 2bx}{x^4} \]
Semplificando per \(x\) (poiché il punto è \(x=1 \neq 0\)):
\[ f'(x) = \frac{-ax - 2b}{x^3} \]
Imponiamo la condizione \(f'(1) = -4\):
\[ f'(1) = \frac{-a(1) - 2b}{1^3} = -a - 2b \]
Quindi:
\[ -a - 2b = -4 \quad \text{...(Eq. II)} \]
Sistema di equazioni:
Risolviamo il sistema formato da (I) e (II):
\[ \begin{cases} a + b = 3 & \text{(I)} \\ -a - 2b = -4 & \text{(II)} \end{cases} \]
Sommando le due equazioni membro a membro:
\[ (a + b) + (-a - 2b) = 3 + (-4) \quad \Rightarrow \quad -b = -1 \quad \Rightarrow \quad b = 1 \]
Sostituendo \(b=1\) nella (I):
\[ a + 1 = 3 \quad \Rightarrow \quad a = 2 \]
Risposta: I parametri sono \(a = 2\) e \(b = 1\).
1. Dominio
Il denominatore deve essere non nullo: \(x^2 \neq 0 \implies x \neq 0\).
\[ D = \mathbb{R} - \{0\} \]
2. Intersezioni e Segno
3. Limiti e Asintoti
\[ \lim_{x \to 0^\pm} f(x) = \lim_{x \to 0^\pm} \frac{2x + 1}{x^2} = \frac{1}{0^+} = +\infty \]
La retta \(x=0\) (asse y) è un **asintoto verticale**.
\[ \lim_{x \to \pm\infty} f(x) = \lim_{x \to \pm\infty} \frac{2x}{x^2} = \lim_{x \to \pm\infty} \frac{2}{x} = 0 \]
La retta \(y=0\) (asse x) è un **asintoto orizzontale**. Quindi non ci sono asintoti obliqui.
4. Derivata prima (Monotonia)
Abbiamo già calcolato \(f'(x) = \frac{-2x - 2}{x^3} = \frac{-2(x+1)}{x^3}\).
Punti critici: \(f'(x) = 0 \implies -2(x+1) = 0 \implies x = -1\).
Studio del segno di \(f'(x)\):
| Intervallo | \(-2(x+1)\) | \(x^3\) | \(f'(x)\) | \(f(x)\) |
|---|---|---|---|---|
| \(x < -1\) | + | - | - | Decrescente \(\searrow\) |
| \(-1 < x < 0\) | - | - | + | Crescente \(\nearrow\) |
| \(x > 0\) | - | + | - | Decrescente \(\searrow\) |
In \(x = -1\), la funzione passa da decrescente a crescente, quindi è un **Minimo Relativo**.
Valore del minimo: \(f(-1) = \frac{2(-1) + 1}{(-1)^2} = \frac{-1}{1} = -1\).
Minimo: \(M_{rel}(-1, -1)\)
5. Derivata seconda (Concavità e Flessi)
Calcoliamo la derivata seconda (partendo da \(f'(x) = -2x^{-2} - 2x^{-3}\)):
\[ f''(x) = 4x^{-3} + 6x^{-4} = \frac{4}{x^3} + \frac{6}{x^4} = \frac{4x + 6}{x^4} = \frac{2(2x + 3)}{x^4} \]
Punti di flesso: \(f''(x) = 0 \implies 2x + 3 = 0 \implies x = -\frac{3}{2}\) (\(-1,5\)).
Studio del segno di \(f''(x)\) (dipende dal segno di \(2x+3\) poiché \(x^4 > 0\)):
In \(x = -\frac{3}{2}\), la funzione presenta un **Punto di Flesso**.
Valore del flesso: \(f\left(-\frac{3}{2}\right) = \frac{2(-\frac{3}{2}) + 1}{(-\frac{3}{2})^2} = \frac{-3 + 1}{\frac{9}{4}} = \frac{-2}{\frac{9}{4}} = -\frac{8}{9} \approx -0,89\).
Flesso: \(F\left(-\frac{3}{2}, -\frac{8}{9}\right)\)
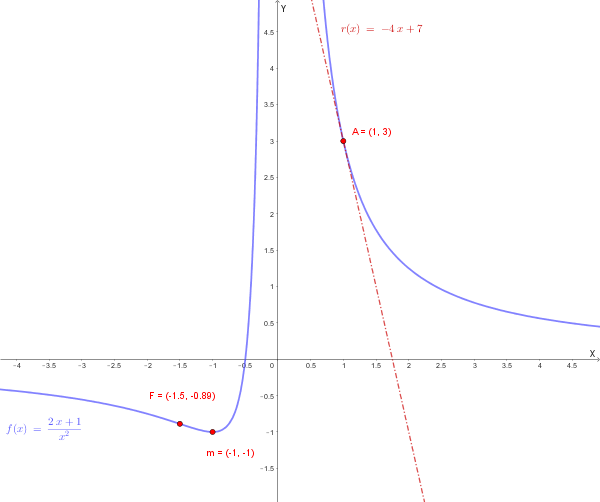
Il grafico mostrerà una funzione che è positiva per \(x > -1/2\) e negativa per \(x < -1/2\). Ha un asintoto verticale in \(x=0\) e orizzontale in \(y=0\). Presenta un minimo relativo, che anche assoluto, in \(m=(-1, -1)\) e un punto di flesso a sinistra del minimo in \(F=(-1,5; -0,89)\).
Il grafico della funzione è il seguente:
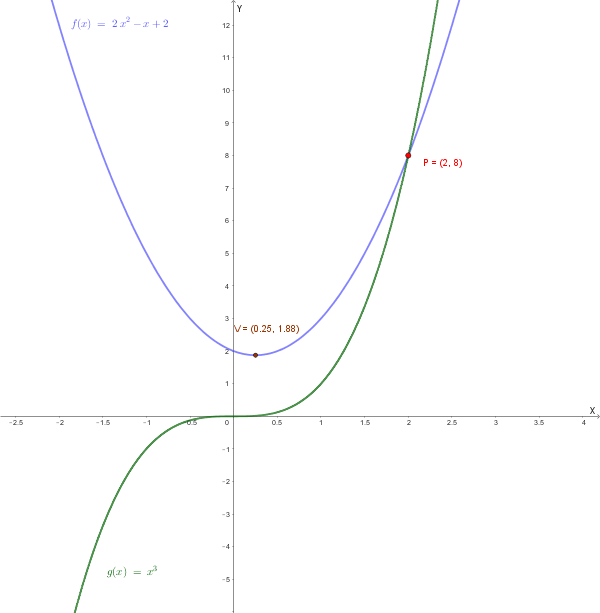
Dopo aver rappresentato graficamente nello stesso piano cartesiano le funzioni di equazioni \(f(x)=2x^2-x+2\) e \(g(x)=x^3\), trova l'angolo sotto cui si tagliano i due grafici.
Analizziamo le due funzioni da rappresentare:
Rappresentiamo le due curve nello stesso piano cartesiano:
Troviamo i punti in cui si intersecano risolvendo \(f(x) = g(x)\):
\[ 2x^2 - x + 2 = x^3 \] \[ x^3 - 2x^2 + x - 2 = 0 \]
Raccogliamo a fattore parziale:
\[ x^2(x - 2) + 1(x - 2) = 0 \] \[ (x^2 + 1)(x - 2) = 0 \]
L'unico fattore che si annulla per valori reali è \(x - 2 = 0\), quindi \(x_0 = 2\).
La coordinata \(y\) è \(y_0 = g(2) = 2^3 = 8\).
Il punto di intersezione è \(P(2, 8)\).
Calcoliamo le derivate prime delle due funzioni per trovare i coefficienti angolari delle tangenti nel punto \(P(2, 8)\).
Per \(f(x)\):
\[ f'(x) = 4x - 1 \] \[ m_f = f'(2) = 4(2) - 1 = 7 \]
Per \(g(x)\):
\[ g'(x) = 3x^2 \] \[ m_g = g'(2) = 3(2)^2 = 12 \]
Indicato co \(\alpha\) il minore tra i due angoli formati dalle rette tangenti, lo si calcola con la formula:
\[ \tan(\alpha) = \left| \frac{m_g - m_f}{1 + m_f m_g} \right| \]
Sostituendo \(m_f = 7\) e \(m_g = 12\):
\[ \tan(\alpha) = \left| \frac{12 - 7}{1 + (7)(12)} \right| = \left| \frac{5}{1 + 84} \right| = \frac{5}{85} = \frac{1}{17} \]
L'angolo \(\alpha\) è:
\[ \alpha = \arctan\left(\frac{1}{17}\right) \]
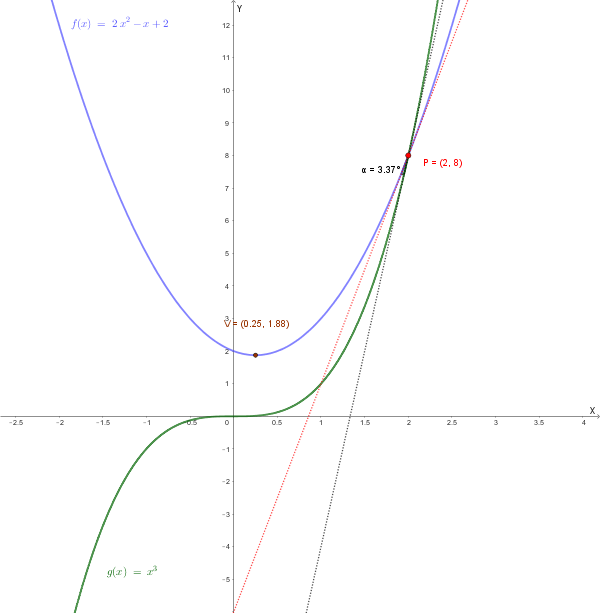
Risposta: L'angolo (il minore) sotto cui si tagliano i due grafici è \(\alpha = \arctan\left(\frac{1}{17}\right) \approx 3,37^\circ\).
Il grafico mostra le due funzioni, \(f(x)\) (parabola) e \(g(x)\) (cubica), che si toccano solo nel punto \(P(2, 8)\). L'angolo formato dalle tangenti in P, che è l'angolo sotto cui si tagliano i due grafici in P, è molto piccolo.
a) Determina il valore del, parametro reale \(a\) in modo che la curva di equazione \(y=f(x)=ax^3-x+4\) abbia nel punto \(T\) di ascissa \(x_T=1\) la tangente \(t\) che formi con la bisettrice \(r\) del secondo e quarto quadrante del piano cartesio \(Oxy\) un angolo \(\alpha\) di ampiezza \(45^\circ\).
b) Studia in modo esauriente la funzione ottenuta e rappresentala graficamente. È richiesto esplicitamente un valore approssimato a meno di un decimo dell'ascissa del punto di intersezione del grafico della funzione con l'asse delle \(x\).
c) Indicato con \(B\) il punto di intersezione fra le rette \(r\) e \(t\), trova l'equazione della parabola \(p\) passante per \(O\), \(B\) e \(T\).
d) Calcola infine l'area del segmento parabolico individuato dalla parabola \(p\) e dalla retta \(t\).
La bisettrice \(r\) ha equazione \(y = -x\), quindi \(m_r = -1\).
La derivata prima è \(f'(x) = 3ax^2 - 1\). Il coefficiente angolare della tangente \(t\) in \(x_T=1\) è \(m_t = 3a(1)^2 - 1 = 3a - 1\).
L'angolo \(\alpha = 45^\circ\) formato tra \(t\) e \(r\) soddisfa \(\tan(\alpha)=1\):
\[ 1 = \left| \frac{m_t - m_r}{1 + m_t m_r} \right| = \left| \frac{(3a - 1) - (-1)}{1 + (3a - 1)(-1)} \right| = \left| \frac{3a}{2 - 3a} \right| \]
Risolviamo l'equazione con il valore assoluto \(1 = \left| \frac{3a}{2 - 3a} \right|\), che si sdoppia in due casi:
\[ 3a = 2 - 3a \] \[ 6a = 2 \] \[ a = \frac{2}{6} = \frac{1}{3} \]
\[ 3a = -(2 - 3a) \] \[ 3a = -2 + 3a \] \[ 0 = -2 \]
Questo caso è impossibile, quindi l'unica soluzione accettabile è quella trovata nel primo caso.
**Risposta a):** L'unico valore del parametro che soddisfa la condizione è \(a = \frac{1}{3}\).
1. Dominio: \(D = \mathbb{R}\).
2. Intersezioni e Segno:
3. Limiti e Asintoti: \(\lim_{x \to \pm\infty} f(x) = \pm\infty\). Non ci sono asintoti.
4. Derivata prima (Monotonia):
\[ f'(x) = x^2 - 1 \]
5. Zero della funzione (Approssimazione)
Lo studio dei limiti e della monotonia della funzione ci permette di dire che la funzione ha un solo zero, che è negativo, poiché il massimo relativo in \(x=-1\) è \(f(-1) \approx 4,67 > 0\) e per \(x \to -\infty\) la funzione tende a \(-\infty\).
Per trovare un'approssimazione a meno di un decimo procediamo ad una tabulazione:
| \(x\) | \(f(x) = \frac{1}{3}x^3 - x + 4\) | Segno |
|---|---|---|
| \(0\) | \(4\) | \(+\) |
| \(-1\) | \(14/3 \approx 4,67\) | \(+\) |
| \(-2\) | \(10/3 \approx 3,33\) | \(+\) |
| \(-3\) | \(-2\) | \(-\) |
Dal cambio di segno tra \(f(-2)\) e \(f(-3)\), deduciamo che la radice richiesta si trova fra \(-3\) e \(-2\).
Affinando la ricerca a meno di un decimo:
| \(x\) | \(f(x)\) (approssimato) | Segno |
|---|---|---|
| \(-2,9\) | \(-1,23\) | \(-\) |
| \(-2,8\) | \(-0,52\) | \(-\) |
| \(-2,7\) | \(0,14\) | \(+\) |
Poiché \(f(-2,8) < 0\) e \(f(-2,7) > 0\), la radice richiesta è compresa tra \(-2,8\) e \(-2,7\).
**Valore approssimato (a meno di un decimo):**
6. Derivata seconda (Concavità e Flessi):
\[ f''(x) = 2x \]
Grafico della funzione:
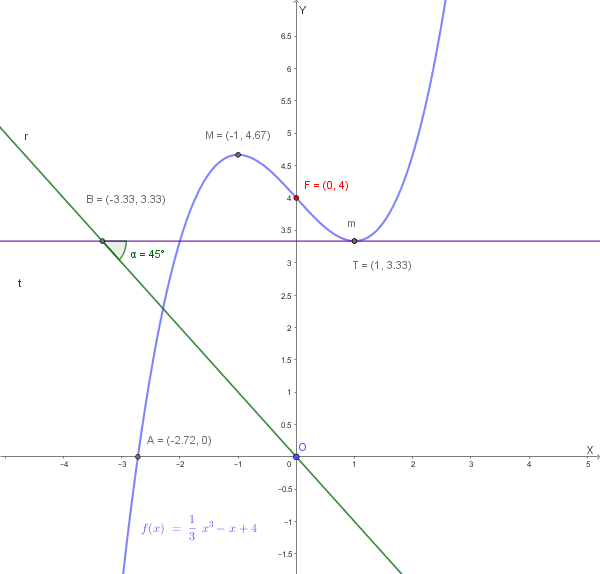
Il punto di tangenza è \(T(1, f(1)) = T(1, 10/3)\).
1. Retta Tangente \(t\):
Il coefficiente angolare è \(m_t = f'(1) = 1^2 - 1 = 0\). L'equazione della retta orizzontale \(t\) è:
\[ t: y = \frac{10}{3} \]
2. Punto \(B\) (Intersezione tra \(t\) e \(r\)):
Intersezione tra \(t: y = 10/3\) e la bisettrice \(r: y = -x\): \(x = -10/3\).
Il punto di intersezione è \(B(-10/3, 10/3)\).
3. Equazione della Parabola \(p\):
La parabola \(p: y = Ax^2 + Bx + C\) passa per \(O(0, 0)\), \(B(-10/3, 10/3)\) e \(T(1, 10/3)\).
Risolvendo il sistema si ottiene \(A = 1\) e \(B = 7/3\).
**Risposta c):** L'equazione della parabola \(p\) è \(y = x^2 + \frac{7}{3}x\).
Il segmento parabolico è individuato dalla parabola \(p: y = x^2 + \frac{7}{3}x\) e dalla retta \(t: y = \frac{10}{3}\).
1. Studio della parabola \(p\)
Equazione: \(y = x^2 + \frac{7}{3}x\). È una parabola con asse verticale e vertice \(V_p\).
2. Segmento parabolico e rettangolo circoscritto
La retta \(t\) ha equazione \(y = \frac{10}{3}\). I punti di intersezione della parabola \(p\) con la retta \(t\) sono \(B(-10/3, 10/3)\) e \(T(1, 10/3)\).
\[ \text{Base} = |x_T - x_B| = \left| 1 - \left(-\frac{10}{3}\right) \right| = \left| 1 + \frac{10}{3} \right| = \frac{13}{3} \]
\[ \text{Altezza} = y_t - y_{V_p} = \frac{10}{3} - \left(-\frac{49}{36}\right) = \frac{120}{36} + \frac{49}{36} = \frac{169}{36} \]
Secondo il Teorema di Archimede, l'area del segmento parabolico è i \(\frac{2}{3}\) dell'area del rettangolo circoscritto.
\[ \text{Area del Rettangolo} = \text{Base} \times \text{Altezza} = \frac{13}{3} \times \frac{169}{36} = \frac{2197}{108} \]
\[ \text{Area del Segmento Parabolico} = \frac{2}{3} \times \text{Area del Rettangolo} = \frac{2}{3} \times \frac{2197}{108} = \frac{2197}{162} \]
**Risposta d):** L'area del segmento parabolico è \(\text{Area} = \frac{2197}{162}\).
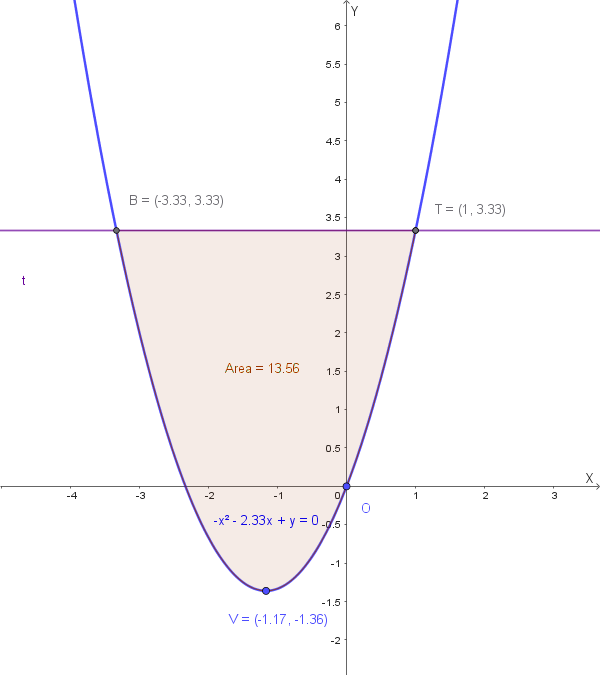
Il grafico della parabola con il segmento parabolico evidenziato è il seguente:
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.