



Questo compito è stato assegnato il giorno 11 Ottobre 2007 a una classe 5ª del Liceo Scientifico.
Argomenti: Proprietà degli insiemi di numeri reali. Dominio di una funzione, grafico di una funzione definita per casi, Funzione inversa, Funzione composta.
Dato l'insieme di numeri reali \(E = \{x \in \mathbb{R} \mid x = \ln(e \cdot n + 1) - \ln(n), \, n \in \mathbb{N}_0\}\), dimostrare, servendosi della definizione, che \(E\) ammette \(1\) come estremo inferiore.
Dato: \(E = \{x \in \mathbb{R} \mid x = \ln(e \cdot n + 1) - \ln(n), \, n \in \mathbb{N}_0\}\)
Da dimostrare: \(\inf(E) = 1\)
Passo 1: Semplificare l'espressione generale degli elementi di E
Per \(n \in \mathbb{N}_0 = \{1, 2, 3, \ldots\}\) (escludo lo 0 perché \(\ln(0)\) non è definito):
\[x_n = \ln(e \cdot n + 1) - \ln(n) = \ln\left(\frac{e \cdot n + 1}{n}\right) = \ln\left(e + \frac{1}{n}\right)\]Passo 2: Calcolare alcuni valori per comprendere il comportamento di E
Passo 3: Dimostrare che 1 è estremo inferiore usando la definizione
Definizione: Un numero reale \(m\) è estremo inferiore di un insieme \(A\) se:
Verifica della condizione 1: \(1\) è minorante di \(E\)
Dobbiamo dimostrare che \(\forall n \in \mathbb{N}_0: x_n \geq 1\)
\[x_n = \ln\left(e + \frac{1}{n}\right) \geq \ln(e) = 1\]Questo è vero perché \(e + \frac{1}{n} > e\) per ogni \(n \geq 1\) e la funzione \(\ln\) è strettamente crescente.
Verifica della condizione 2: \(1\) è il massimo dei minoranti
Dobbiamo dimostrare che per ogni \(\varepsilon > 0\) esiste \(x \in E\) tale che \(x <1 + \varepsilon\).
Dato \(\varepsilon > 0\), vogliamo trovare \(n\) tale che:
\[\ln\left(e + \frac{1}{n}\right) <1 + \varepsilon\] \[e + \frac{1}{n} < e^{1 + \varepsilon} = e \cdot e^{\varepsilon}\] \[\frac{1}{n} < e \cdot e^{\varepsilon} - e = e(e^{\varepsilon} - 1)\] \[n > \frac{1}{e(e^{\varepsilon} - 1)}\]Poiché \(e^{\varepsilon} - 1 > 0\) per ogni \(\varepsilon > 0\), il numero \(\frac{1}{e(e^{\varepsilon} - 1)}\) è ben definito e positivo. Scegliendo un intero \(n\) sufficientemente grande (maggiore di questo valore), otteniamo \(x_n < 1 + \varepsilon\).
Conclusione:
Avendo verificato entrambe le condizioni della definizione, concludiamo che:
\[\boxed{\inf(E) = 1}\]Sono date le seguenti funzioni:
\[f(x) = \begin{cases} x + 1 & \text{se } x \geq 1 \\ 1 - x & \text{se } x < 1 \end{cases}\]
\[g(x) = \sqrt{x}\]
Trovare le funzioni composte \(f \circ g\) e \(g \circ f\) e rappresentarle graficamente.
Date:
\[f(x) = \begin{cases} x + 1 & \text{se } x \geq 1 \\ 1 - x & \text{se } x < 1 \end{cases}\]
\[g(x) = \sqrt{x}, \quad \text{con dominio } D_g = [0, +\infty)\]
Parte 1: Funzione composta \(f \circ g\)
La funzione composta \((f \circ g)(x) = f(g(x)) = f(\sqrt{x})\) è definita per \(x \in D_g = [0, +\infty)\).
Per determinare \(f(\sqrt{x})\), dobbiamo verificare quando \(\sqrt{x} \geq 1\) e quando \(\sqrt{x} < 1\):
Quindi:
\[(f \circ g)(x) = \begin{cases} 1 - \sqrt{x} & \text{se } 0 \leq x < 1 \\ \sqrt{x} + 1 & \text{se } x \geq 1 \end{cases}\]
con dominio \(D_{f \circ g} = [0, +\infty)\).
Parte 2: Funzione composta \(g \circ f\)
La funzione composta \((g \circ f)(x) = g(f(x)) = \sqrt{f(x)}\) è definita quando \(f(x) \geq 0\).
Studio del segno di \(f(x)\):
Quindi \(f(x) \geq 0\) per ogni \(x \in \mathbb{R}\), e il dominio di \(g \circ f\) è \(D_{g \circ f} = \mathbb{R}\).
Calcoliamo \(g(f(x))\):
Quindi:
\[(g \circ f)(x) = \begin{cases} \sqrt{1 - x} & \text{se } x < 1 \\ \sqrt{x + 1} & \text{se } x \geq 1 \end{cases}\]
con dominio \(D_{g \circ f} = \mathbb{R}\).
Parte 3: Rappresentazione grafica
Grafico di \(f \circ g\):
Grafico di \(a(x) = f \circ g\):
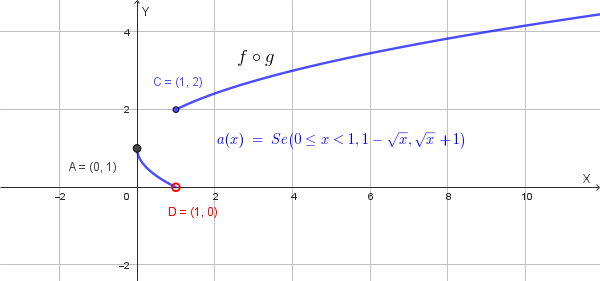
Grafico di \(g \circ f\):
Punti notevoli:
Per \(f \circ g\):
Per \(g \circ f\):
Grafico di \(b(x) = g \circ f\):
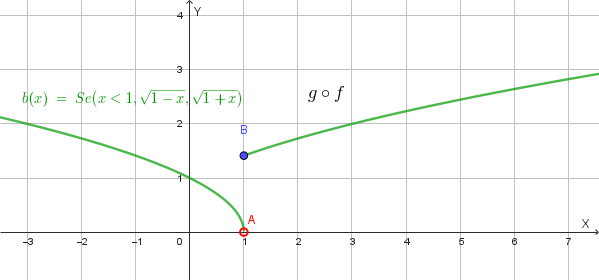
Conclusione:
\[\boxed{(f \circ g)(x) = \begin{cases} 1 - \sqrt{x} & \text{se } 0 \leq x < 1 \\ \sqrt{x} + 1 & \text{se } x \geq 1 \end{cases}}\]
\[\boxed{(g \circ f)(x) = \begin{cases} \sqrt{1 - x} & \text{se } x < 1 \\ \sqrt{x + 1} & \text{se } x \geq 1 \end{cases}}\]
Si consideri la funzione di equazione \(f(x) = \frac{1}{2^{x-1}}\).
a) Tracciare il grafico della funzione e determinare il dominio e l'immagine della funzione.
b) Spiegare perché la funzione è invertibile.
c) Trovare l'equazione della funzione inversa \(x = f^{-1}(y) = g(y)\).
d) Rappresentare graficamente la funzione \(y = g(x)\).
a) Grafico, dominio e immagine della funzione \(f(x) = \frac{1}{2^{x-1}}\)
Riscriviamo la funzione: \(f(x) = \frac{1}{2^{x-1}} = \left(\frac{1}{2}\right)^{x-1}\)
Dominio: \(D_f = \mathbb{R}\) (tutti i numeri reali, poiché l'esponenziale è definita ovunque)
Immagine: \(Im_f = (0, +\infty)\) (la funzione è sempre positiva)
Caratteristiche del grafico:
Il grafico della funzione si ottiene da quello di \(a(x) = \left(\frac{1}{2}\right)^x\) mediante una traslazione verso destra di 1. Questo è il grafico:
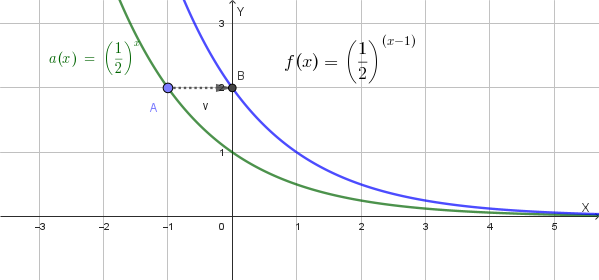
b) Perché la funzione è invertibile
La funzione \(f(x) = \frac{1}{2^{x-1}}\) è invertibile perché è strettamente decrescente, quindi è biunivoca.
c) Funzione inversa \(x = f^{-1}(y) = g(y)\)
Per trovare la funzione inversa, partiamo da \(y = \frac{1}{2^{x-1}}\) e ricaviamo \(x\):
\(y = \frac{1}{2^{x-1}}\)
\(2^{x-1} = \frac{1}{y}\)
Applicando il logaritmo in base 2:
\(x - 1 = \log_2\left(\frac{1}{y}\right) = \log_2(y^{-1}) = -\log_2(y)\)
\(x = 1 - \log_2(y)\)
Quindi: \(\boxed{g(y) = 1 - \log_2(y)}\) con dominio \(y \in (0, +\infty)\)
In forma più comune: \(g(x) = 1 - \log_2(x)\) per \(x > 0\)
d) Grafico della funzione inversa \(y = g(x) = 1 - \log_2(x)\)
Caratteristiche del grafico di \(g(x) = 1 - \log_2(x)\):
Mostriamo il grafico di \(y = g(x)\) insieme al grafico di \(y = f(x)\) e della retta \(y = x\):
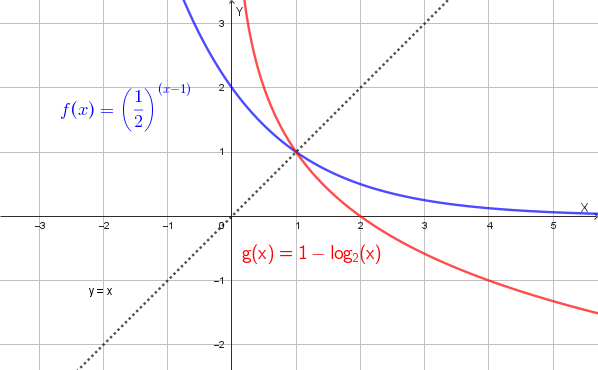
Trovare il dominio della seguente funzione:
\(y = f(x) = \sqrt{1-x^2} + e^{\frac{1}{x}} - \ln(1-x)\)
Per trovare il dominio di \(f(x) = \sqrt{1-x^2} + e^{\frac{1}{x}} - \ln(1-x)\), dobbiamo analizzare separatamente le condizioni di esistenza di ogni termine:
1) Termine \(\sqrt{1-x^2}\):
La radice quadrata è definita solo quando l'argomento è non negativo:
\(1-x^2 \geq 0\)
\(-x^2 \geq -1\)
\(x^2 \leq 1\)
\(-1 \leq x \leq 1\)
Condizione: \(x \in [-1, 1]\)
2) Termine \(e^{\frac{1}{x}}\):
L'esponenziale è sempre definita, ma la frazione \(\frac{1}{x}\) richiede:
\(x \neq 0\)
Condizione: \(x \in \mathbb{R} \setminus \{0\}\)
3) Termine \(-\ln(1-x)\):
Il logaritmo naturale è definito solo quando l'argomento è strettamente positivo:
\(1-x > 0\)
\(-x > -1\)
\(x < 1\)
Condizione: \(x \in (-\infty, 1)\)
Intersezione delle condizioni:
Risolviamo il sistema:
\[\begin{cases} 1-x^2 \geq 0 \\ x \neq 0 \\ 1-x > 0 \end{cases}\]
Risoluzione del sistema:
Prima disequazione: \(1-x^2 \geq 0 \Rightarrow x^2 \leq 1 \Rightarrow -1 \leq x \leq 1\)
Seconda condizione: \(x \neq 0\)
Terza disequazione: \(1-x > 0 \Rightarrow x < 1\)
Schema grafico delle soluzioni:
L'intersezione del sistema ci dà:
\(D_f = [-1, 1] \cap (\mathbb{R} \setminus \{0\}) \cap (-\infty, 1) = [-1, 0) \cup (0, 1)\)
Dominio finale:
\(\boxed{D_f = [-1, 0) \cup (0, 1)}\)
Osservazioni:
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.