Compito in Classe di Matematica

Soluzione Esercizio 1

Per determinare le proprietà richieste dell'insieme \(E\), dobbiamo prima analizzare la funzione che genera i suoi elementi:

\[ x_n = \frac{n^2+3n+2}{n^2+2n} \]

dove \(n \in \mathbb{N}_0\). Dato che \(n^2+2n = n(n+2)\) si annullerebbe per \(n=0\), considereremo \(n \in \{1, 2, 3, \dots\}\) per la validità della frazione.

Possiamo semplificare l'espressione di \(x_n\):

\[ x_n = \frac{(n+1)(n+2)}{n(n+2)} \]

Per \(n \ne -2\) (e quindi per \(n \in \mathbb{N}, n \ge 1\)), possiamo semplificare il termine \((n+2)\):

\[ x_n = \frac{n+1}{n} \]

Ora, possiamo riscrivere \(x_n\) in una forma più utile per l'analisi:

\[ x_n = 1 + \frac{1}{n} \]

Analizziamo l'andamento di \(x_n\) per \(n \in \{1, 2, 3, \dots\}\):

• Per \(n=1\), \(x_1 = 1 + \frac{1}{1} = 2\).
• Per \(n=2\), \(x_2 = 1 + \frac{1}{2} = 1.5\).
• Per \(n=3\), \(x_3 = 1 + \frac{1}{3} \approx 1.33\).

All'aumentare di \(n\), il termine \(\frac{1}{n}\) diminuisce e si avvicina a 0. Di conseguenza, \(x_n\) diminuisce e si avvicina a 1.

L'insieme \(E\) è quindi:

\[ E = \left\{2, 1.5, 1.333\dots, 1.25, 1.2, \dots\right\} \]

o più precisamente, \(E = \left\{1+\frac{1}{n} \mid n \in \mathbb{N}, n \ge 1\right\}\).

1. Estremo superiore (sup E): Ricordiamo che l'estremo superiore di un insieme \(E\) è il più piccolo dei maggioranti di \(E\). Il più piccolo maggiorante è \(M\) tale che tutti gli elementi di \(E\) sono minori o uguali a \(M\), e per ogni \(\epsilon > 0\), esiste almeno un elemento \(x \in E\) tale che \(x > M - \epsilon\). Nel nostro caso, il valore più grande che la funzione assume è quando \(n\) è il più piccolo possibile, cioè \(n=1\).

   \[ \text{sup } E = x_1 = 2 \]

2. Massimo (max E): Poiché il valore \(2\) è effettivamente raggiunto dall'insieme (per \(n=1\)), allora \(2\) è il massimo di \(E\).

   \[ \text{max } E = 2 \]

3. Estremo inferiore (inf E): Ricordiamo che l'estremo inferiore di un insieme \(E\) è il più grande dei minoranti di \(E\). Il più grande minorante è \(m\) tale che tutti gli elementi di \(E\) sono maggiori o uguali a \(m\), e per ogni \(\epsilon > 0\), esiste almeno un elemento \(x \in E\) tale che \(x < m + \epsilon\). Nel nostro caso, quando \(n \to \infty\), \(x_n \to 1\). Nessun elemento di \(E\) sarà mai uguale a 1, ma si avvicinerà arbitrariamente ad esso.

   \[ \text{inf } E = 1 \]

4. Minimo (min E): Poiché il valore \(1\) non è mai raggiunto dall'insieme \(E\) (infatti \(\frac{n+1}{n} = 1 \implies n+1=n \implies 1=0\), che è impossibile), l'insieme non ha minimo.

5. Punti di accumulazione: Ricordiamo che un punto \(c\) (che può appartenere o no all'insieme) è di accumulazione per un insieme \(E\) se in ogni intorno di \(c\) (escluso eventualmente \(c\) stesso) cade almeno un elemento di \(E\), e di conseguenza ne cadono infiniti. Nel nostro caso, l'unico valore che soddisfa questa proprietà è \(c=1\). Quindi:

   \[ \text{Punti di accumulazione di } E = \{1\} \]

6. Punti isolati: Ogni elemento dell'insieme \(E\) (cioè ogni \(x_n\)) è un punto isolato, perché per ogni \(x_n\) possiamo trovare un intorno che non contiene altri punti di \(E\) se non \(x_n\) stesso. L'insieme \(E\) è costituito da punti distinti che si avvicinano a 1. Tutti i punti \(x_n = 1+\frac{1}{n}\) per \(n \in \mathbb{N}, n \ge 1\) sono punti isolati di \(E\).

   \[ \text{Punti isolati di } E = E = \left\{1+\frac{1}{n} \mid n \in \mathbb{N}, n \ge 1\right\} \]

7. Punti interni: L'insieme \(E\) è un insieme di punti discreti (una successione). Un punto è interno se esiste un intorno del punto che è interamente contenuto nell'insieme. Non è possibile trovare un intorno di nessun punto \(x_n \in E\) che contenga solo punti di \(E\). Pertanto, l'insieme dei punti interni di \(E\) è l'insieme vuoto (\(\emptyset\)).

   \[ \text{Int}(E) = \emptyset \]

8. Punti esterni: Un punto è esterno all'insieme \(E\) se esiste un intorno del punto che non interseca \(E\). Tutti i numeri reali che non sono in \(E\) e che non sono il punto di accumulazione \(1\) sono punti esterni.

   \[ \text{Est}(E) = \mathbb{R} \setminus (E \cup \{1\}) \]

9. Frontiera di E : La frontiera di un insieme è l'insieme dei punti che non sono né interni né esterni. In questo caso, la frontiera di \(E\) è l'unione dei punti di accumulazione e dei punti isolati di \(E\). Essa può essere indicata anche con la **chiusura dell'insieme E**, \(\overline{E}\).

   \[ \overline{E} = E \cup \{1\} = \left\{1+\frac{1}{n} \mid n \in \mathbb{N}, n \ge 1\right\} \cup \{1\} \]

Soluzione Esercizio 2

Per l'insieme dato:

\[ E=\left\{x \in \mathbb{R} \mid x=\frac{2n+1}{n}, n \in \mathbb{N}_0\right\} \]

Come abbiamo discusso per l'esercizio precedente, per \(n \in \mathbb{N}_0\), se consideriamo che il denominatore non può essere zero, allora \(n \ge 1\). Se l'insieme include \(n=0\), la frazione non è definita. Pertanto, assumeremo \(n \in \{1, 2, 3, \dots\}\).

Possiamo riscrivere l'espressione di \(x_n\):

\[ x_n = \frac{2n+1}{n} = \frac{2n}{n} + \frac{1}{n} = 2 + \frac{1}{n} \]

Ora analizziamo l'andamento di \(x_n\) per \(n \in \{1, 2, 3, \dots\}\):

• Per \(n=1\), \(x_1 = 2 + \frac{1}{1} = 3\).
• Per \(n=2\), \(x_2 = 2 + \frac{1}{2} = 2.5\).
• Per \(n=3\), \(x_3 = 2 + \frac{1}{3} \approx 2.33\).

All'aumentare di \(n\), il termine \(\frac{1}{n}\) diminuisce e si avvicina a \(0\). Di conseguenza, \(x_n\) diminuisce e si avvicina a \(2\).

1. Dimostrazione che \(2\) è l'estremo inferiore:

   Per dimostrare che \(2\) è l'estremo inferiore di \(E\), dobbiamo mostrare due cose:

   • \(2\) è un minorante per \(E\): Dobbiamo dimostrare che per ogni elemento \(x_n \in E\), si ha \(x_n \ge 2\).
     Sappiamo che \(x_n = 2 + \frac{1}{n}\). Poiché \(n \in \mathbb{N}, n \ge 1\), il termine \(\frac{1}{n}\) è sempre maggiore di \(0\) (cioè \(\frac{1}{n} > 0\)).
     Quindi, \(2 + \frac{1}{n} > 2\). Questo implica che \(x_n > 2\) per ogni \(n \ge 1\).
     Dato che ogni elemento di \(E\) è strettamente maggiore di \(2\), allora \(2\) è sicuramente un minorante per \(E\).

   • \(2\) è il più grande dei minoranti (o per ogni \(\epsilon > 0\), esiste un elemento di \(E\) minore di \(2 + \epsilon\)): Dobbiamo dimostrare che non esiste un minorante più grande di \(2\). Questo si fa mostrando che, per ogni numero \(\epsilon > 0\), esiste un elemento \(x_n \in E\) tale che \(x_n < 2 + \epsilon\).
     Vogliamo trovare un \(n\) tale che:

     \[ 2 + \frac{1}{n} < 2 + \epsilon \]

     Sottraendo \(2\) da entrambi i lati otteniamo:

     \[ \frac{1}{n} < \epsilon \]

     Prendendo il reciproco di entrambi i lati (e invertendo il segno della disuguaglianza, dato che entrambi i lati sono positivi):

     \[ n > \frac{1}{\epsilon} \]

     Poiché \(\epsilon > 0\), \(\frac{1}{\epsilon}\) è un numero reale positivo. Esisterà sempre un numero naturale \(n\) maggiore di \(\frac{1}{\epsilon}\).
     Questo significa che, non importa quanto piccolo sia \(\epsilon\) (purché positivo), possiamo sempre trovare un \(n\) sufficientemente grande tale che \(x_n = 2 + \frac{1}{n}\) sia più vicino a \(2\) di \(\epsilon\).
     Per esempio, se \(\epsilon = 0.1\), possiamo scegliere \(n > 1/0.1 = 10\), quindi \(n=11\) (per cui \(x_{11} = 2 + 1/11 \approx 2.09\), che è minore di \(2.1\)).
     Pertanto, \(2\) è il più grande dei minoranti, e quindi l'estremo inferiore di \(E\).

     \[ \text{inf } E = 2 \]

2. \(2\) è un punto di accumulazione per \(E\)?

   Ricordiamo che un punto \(c\) è di accumulazione per un insieme \(E\) se ogni intorno di \(c\) (escluso eventualmente \(c\) stesso) contiene almeno un elemento di \(E\), e di conseguenza ne contiene infiniti.

   Nel nostro caso, abbiamo visto che \(x_n = 2 + \frac{1}{n}\) e che, all'aumentare di \(n\), \(x_n\) si avvicina sempre di più a \(2\).

   Per ogni intorno di \(2\), non importa quanto piccolo, ci saranno sempre elementi della forma \(2 + \frac{1}{n}\) che cadono in quell'intorno. Per dimostrarlo, consideriamo un intorno generico di \(2\), sia esso \((2-\delta, 2+\delta)\) con \(\delta > 0\). Vogliamo mostrare che esiste sempre un elemento \(x_n \in E\) tale che \(x_n \in (2-\delta, 2+\delta)\) e \(x_n \ne 2\).

   Questo si traduce nel risolvere il seguente sistema di disuguaglianze per \(x_n = 2 + \frac{1}{n}\):

   \[ 2 - \delta < 2 + \frac{1}{n} < 2 + \delta \]

   Analizziamo le due disuguaglianze separatamente:

   • Prima disuguaglianza: \(2 - \delta < 2 + \frac{1}{n}\)
     Sottraendo \(2\) da entrambi i lati otteniamo: \[ -\delta < \frac{1}{n} \]

     Poiché \(n \in \mathbb{N}, n \ge 1\), \(\frac{1}{n}\) è sempre positivo. Dato che \(\delta > 0\), \(-\delta\) è sempre negativo. Una quantità positiva è sempre maggiore di una negativa, quindi questa disuguaglianza è sempre vera per ogni \(n \ge 1\).

   • Seconda disuguaglianza: \(2 + \frac{1}{n} < 2 + \delta\)
     Sottraendo \(2\) da entrambi i lati otteniamo: \[ \frac{1}{n} < \delta \]

     Prendendo il reciproco di entrambi i lati (e invertendo il segno della disuguaglianza, dato che entrambi i lati sono positivi):

     \[ n > \frac{1}{\delta} \]

   Quindi, per qualsiasi \(\delta > 0\) (cioè per qualsiasi intorno di \(2\)), possiamo sempre trovare un numero naturale \(n\) (sufficientemente grande, cioè \(n > 1/\delta\)) tale che l'elemento \(x_n = 2 + \frac{1}{n}\) cada nell'intorno \((2-\delta, 2+\delta)\). Inoltre, poiché \(n \ge 1\), sappiamo che \(x_n = 2 + \frac{1}{n} > 2\), il che significa che \(x_n\) è sempre diverso da \(2\).

   Poiché per ogni \(\delta > 0\) esiste un numero infinito di valori di \(n\) maggiori di \(1/\delta\) (ad esempio, indicando con \(\lfloor 1/\delta \rfloor\) la **parte intera** di \(1/\delta\), i valori di \(n\) potrebbero essere \(\lfloor 1/\delta \rfloor + 1, \lfloor 1/\delta \rfloor + 2, \dots\)), significa che ogni intorno di \(2\) contiene infiniti elementi di \(E\) (tutti diversi da \(2\)).

   Quindi, sì, \(2\) è un punto di accumulazione per \(E\).

   \[ \text{Punti di accumulazione di } E = \{2\} \]

Soluzione Esercizio 3

Per determinare il dominio (o insieme di definizione) della funzione di equazione:

\[ y=f(x)=\frac{\sqrt{x-2}}{\ln(x^2-4x+3)} \]

dobbiamo considerare le condizioni di esistenza di tutte le operazioni presenti nella funzione:

1. Condizione per la radice quadrata: L'argomento della radice quadrata deve essere maggiore o uguale a zero.

   \[ x-2 \ge 0 \implies x \ge 2 \]

2. Condizione per il logaritmo naturale: L'argomento del logaritmo deve essere strettamente maggiore di zero.

   \[ x^2-4x+3 > 0 \]

   Per risolvere questa disequazione di secondo grado, troviamo prima le radici dell'equazione \(x^2-4x+3=0\). Usiamo la formula risolutiva:

   \[ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \frac{4 \pm \sqrt{(-4)^2 - 4(1)(3)}}{2(1)} = \frac{4 \pm \sqrt{16 - 12}}{2} = \frac{4 \pm 2}{2} \]

   Le due radici sono:

   \[ x_1 = \frac{4-2}{2} = \frac{2}{2} = 1 \]

   \[ x_2 = \frac{4+2}{2} = \frac{6}{2} = 3 \]

   Quindi la disequazione \(x^2-4x+3 > 0\) è soddisfatta per i valori esterni alle radici:

   \[ x < 1 \quad \text{o} \quad x > 3 \]

3. Condizione per il denominatore: Il denominatore della frazione non può essere uguale a zero.

   \[ \ln(x^2-4x+3) \ne 0 \]

   Affinché un logaritmo sia zero, il suo argomento deve essere uguale a 1. Quindi:

   \[ x^2-4x+3 \ne 1 \]

   \[ x^2-4x+2 \ne 0 \]

   Risolviamo l'equazione \(x^2-4x+2=0\) per trovare i valori che devono essere esclusi:

   \[ x = \frac{4 \pm \sqrt{(-4)^2 - 4(1)(2)}}{2(1)} = \frac{4 \pm \sqrt{16 - 8}}{2} = \frac{4 \pm 2\sqrt{2}}{2} \]

   I valori da escludere sono:

   \[ x_3 = 2 - \sqrt{2} \approx 2 - 1.414 = 0.586 \]

   \[ x_4 = 2 + \sqrt{2} \approx 2 + 1.414 = 3.414 \]

Ora dobbiamo combinare tutte queste condizioni. Per farlo, possiamo visualizzarle su una linea dei numeri reali:

• Condizione 1: \(x \ge 2\)

  \[ [2, +\infty) \]

• Condizione 2: \(x < 1\) o \(x > 3\)

  \[ (-\infty, 1) \cup (3, +\infty) \]

• Condizione 3 (valori da escludere): \(x \ne 2 - \sqrt{2}\) e \(x \ne 2 + \sqrt{2}\)
  Nota che \(2 - \sqrt{2} \approx 0.586\) e \(2 + \sqrt{2} \approx 3.414\).

Intersecando la Condizione 1 (\(x \ge 2\)) con la Condizione 2 (\(x < 1\) o \(x > 3\)), otteniamo:

• I valori \(x < 1\) sono incompatibili con \(x \ge 2\).
• I valori \(x > 3\) sono compatibili con \(x \ge 2\).

Quindi, l'intersezione delle prime due condizioni è \(x > 3\).

\[ (x \ge 2) \cap (x < 1 \text{ o } x > 3) \implies x > 3 \]

Infine, dobbiamo escludere i valori ottenuti dalla Condizione 3: \(x = 2 - \sqrt{2}\) e \(x = 2 + \sqrt{2}\).

• \(2 - \sqrt{2} \approx 0.586\) non rientra nell'intervallo \(x > 3\), quindi è già escluso.
• \(2 + \sqrt{2} \approx 3.414\) rientra nell'intervallo \(x > 3\). Dobbiamo quindi escluderlo.

L'insieme di definizione finale (dominio) è quindi:

\[ D = \{x \in \mathbb{R} \mid x > 3 \text{ e } x \ne 2 + \sqrt{2}\} \]

Equivalente a:

\[ D = (3, 2 + \sqrt{2}) \cup (2 + \sqrt{2}, +\infty) \]

Soluzione Esercizio 4

Per rappresentare graficamente la funzione \(y=f(x)=x-[x]+1\) nell'intervallo \(-2 \le x \le 2\), dobbiamo capire come si comporta la parte intera di \(x\), indicata con \([x]\). Ricorda che \([x]\) è il più grande intero che non supera \(x\). Questo significa che il valore di \([x]\) cambia ogni volta che \(x\) attraversa un numero intero.

Analizziamo la funzione per intervalli di numeri interi, all'interno dell'intervallo dato \([-2, 2]\).

1. Per \(-2 \le x < -1\):
   In questo intervallo, la parte intera di \(x\) è \([x] = -2\).
   Quindi, la funzione diventa:

   \[ y = x - (-2) + 1 = x + 2 + 1 = x + 3 \]

2. Per \(-1 \le x < 0\):
   In questo intervallo, la parte intera di \(x\) è \([x] = -1\).
   Quindi, la funzione diventa:

   \[ y = x - (-1) + 1 = x + 1 + 1 = x + 2 \]

3. Per \(0 \le x < 1\):
   In questo intervallo, la parte intera di \(x\) è \([x] = 0\).
   Quindi, la funzione diventa:

   \[ y = x - 0 + 1 = x + 1 \]

4. Per \(1 \le x < 2\):
   In questo intervallo, la parte intera di \(x\) è \([x] = 1\).
   Quindi, la funzione diventa:

   \[ y = x - 1 + 1 = x \]

5. Per \(x = 2\):
   Nel punto finale dell'intervallo, \(x=2\), la parte intera di \(x\) è \([x] = 2\).
   Quindi, la funzione diventa:

   \[ y = 2 - 2 + 1 = 1 \]

Riassumendo, la funzione \(y=f(x)\) può essere definita per casi come segue:

\[ f(x) = \begin{cases} x+3 & \text{se } -2 \le x < -1 \\ x+2 & \text{se } -1 \le x < 0 \\ x+1 & \text{se } 0 \le x < 1 \\ x & \text{se } 1 \le x < 2 \\ 1 & \text{se } x = 2 \end{cases} \]

Ogni "pezzo" della funzione è una retta con pendenza 1, che inizia da un punto pieno e finisce con un "buco" (un punto escluso), ad eccezione dell'ultimo intervallo che termina esattamente in \(x=2\).

Quindi il grafico della funzione è:

Soluzione Esercizio 5

Per dimostrare che \(2^{2n+1}+3^{2n+1}\) è divisibile per \(5\) per ogni numero naturale \(n\), useremo due metodi: prima la via diretta e poi l'induzione matematica.

Via Diretta (utilizzando la scomposizione)

Per la dimostrazione diretta, utilizzeremo la formula di scomposizione della somma di due potenze dispari:

Se \(a\) e \(b\) sono numeri e \(k\) è un numero intero positivo dispari, allora \(a^k + b^k\) è sempre divisibile per \((a+b)\).

In altre parole, \(a^k + b^k = (a+b)(a^{k-1} - a^{k-2}b + a^{k-3}b^2 - \dots - ab^{k-2} + b^{k-1})\).

Nel nostro caso, abbiamo l'espressione \(2^{2n+1}+3^{2n+1}\).

Possiamo identificare:

• \(a = 2\)
• \(b = 3\)
• L'esponente \(k = 2n+1\). Poiché \(n\) è un numero naturale (quindi \(n \ge 0\)), l'esponente \(2n+1\) sarà sempre un dispari (\(1, 3, 5, \dots\)).

Applicando la formula di scomposizione, sappiamo che \(2^{2n+1}+3^{2n+1}\) è divisibile per \((a+b)\).

Calcoliamo \(a+b\):

\[ a+b = 2+3 = 5 \]

Questo significa che \(2^{2n+1}+3^{2n+1}\) è sempre divisibile per \(5\).

Quindi, abbiamo dimostrato che \(2^{2n+1}+3^{2n+1}\) è divisibile per 5 per ogni numero naturale \(n\).

Per Induzione Matematica

La dimostrazione per induzione si articola in tre passi:

1. Passo Base: Verificare che la proprietà sia vera per il più piccolo valore di \(n\) (solitamente \(n=0\) o \(n=1\), a seconda della definizione di "numero naturale"). Assumiamo \(n \in \mathbb{N}_0 = \{0, 1, 2, \dots\}\).

   Per \(n=0\):

   \[ 2^{2(0)+1} + 3^{2(0)+1} = 2^1 + 3^1 = 2 + 3 = 5 \]

   Poiché \(5\) è divisibile per \(5\), il passo base è verificato.

2. Passo Induttivo (Ipotesi Induttiva): Assumere che la proprietà sia vera per un generico numero naturale \(n\). Cioè, supponiamo che \(2^{2n+1}+3^{2n+1}\) sia divisibile per \(5\).

   Questo significa che \(2^{2n+1}+3^{2n+1} = 5m\) per qualche intero \(m\).

3. Passo Induttivo (Tesi Induttiva): Dimostrare che la proprietà è vera per \(n+1\). Cioè, dobbiamo dimostrare che \(2^{2(n+1)+1}+3^{2(n+1)+1}\) è divisibile per \(5\).

   Consideriamo l'espressione per \(n+1\):

   \[ 2^{2(n+1)+1}+3^{2(n+1)+1} = 2^{2n+2+1} + 3^{2n+2+1} \]

   \[ = 2^{2n+3} + 3^{2n+3} \]

   \[ = 2^{2n+1} \cdot 2^2 + 3^{2n+1} \cdot 3^2 \]

   \[ = 2^{2n+1} \cdot 4 + 3^{2n+1} \cdot 9 \]

   Ora, cerchiamo di usare l'ipotesi induttiva (\(2^{2n+1}+3^{2n+1} = 5m\)). Possiamo scrivere \(2^{2n+1} = 5m - 3^{2n+1}\). Sostituiamo questo nell'espressione:

   \[ 4(5m - 3^{2n+1}) + 9 \cdot 3^{2n+1} \]

   \[ = 20m - 4 \cdot 3^{2n+1} + 9 \cdot 3^{2n+1} \]

   \[ = 20m + (9 - 4) \cdot 3^{2n+1} \]

   \[ = 20m + 5 \cdot 3^{2n+1} \]

   Raccogliamo il \(5\):

   \[ = 5(4m + 3^{2n+1}) \]

   Poiché \(4m + 3^{2n+1}\) è un numero intero, l'intera espressione è un multiplo di \(5\).

   Questo dimostra che \(2^{2(n+1)+1}+3^{2(n+1)+1}\) è divisibile per \(5\).

Per il principio di induzione matematica, la proprietà è vera per ogni numero naturale \(n\).

Soluzione Esercizio 6

a) Dominio e grafico di \(y=f(x)=\frac{1}{e^{1-x}}\)

Il dominio è tutto \( \mathbb{R} \), poiché il denominatore esiste sempre e non si annulla mai.

Possiamo riscrivere la funzione \(f(x)\) in una forma più semplice:

\[ f(x) = \frac{1}{e^{1-x}} \]

Ricordando che \(\frac{1}{e^a} = e^{-a}\), possiamo scrivere:

\[ f(x) = e^{-(1-x)} = e^{-1+x} = e^{x-1} \]

La funzione \(y=e^{x-1}\) si ottiene dal grafico di \(y=e^x\) tramite una traslazione orizzontale.

• Se l'esponente è \(x-c\) (con \(c > 0\)), la traslazione è di \(c\) unità verso destra.
• Se l'esponente è \(x+c\) (con \(c > 0\)), la traslazione è di \(c\) unità verso sinistra.

Nel nostro caso, l'esponente è \(x-1\), il che significa che il grafico di \(f(x)\) si ottiene dal grafico di \(y=e^x\) mediante una traslazione orizzontale di 1 unità verso destra.

Il grafico di \(f\) è quindi il seguente:

---

b) Funzione Invertibile e Inversa

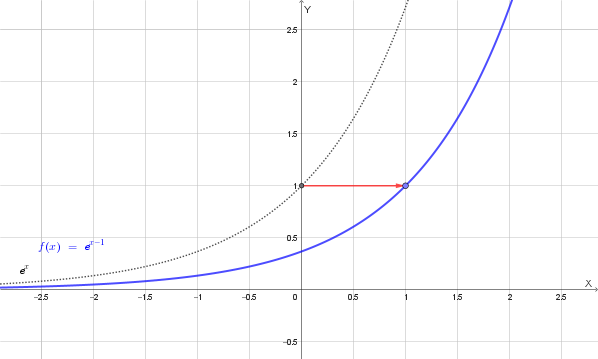
Una funzione è invertibile se è una funzione biunivoca (o biiettiva), il che significa che è sia iniettiva che suriettiva.

Dal grafico deduciamo che la funzione è strettamente crescente in tutto il suo dominio, quindi è invertibile.

Per trovare l'equazione della funzione inversa \(y=g(x)\), seguiamo questi passaggi:

1. Scrivi l'equazione della funzione come \(y = e^{x-1}\).

2. Scambia \(x\) con \(y\): \(x = e^{y-1}\).

3. Risolvi per \(y\). Per isolare \(y\), applichiamo il logaritmo naturale (ln) a entrambi i lati dell'equazione:

   \[ \ln(x) = \ln(e^{y-1}) \]

   Per la proprietà dei logaritmi \(\ln(e^A) = A\):

   \[ \ln(x) = y-1 \]

   \[ y = \ln(x) + 1 \]

Quindi, l'equazione della funzione inversa è \(g(x) = \ln(x) + 1\).

Il grafico della funzione inversa \(y=g(x)\) si ottiene riflettendo il grafico della funzione originale \(y=f(x)\) rispetto alla retta \(y=x\).

---

c) Funzioni Composte \(f \circ h\) e \(h \circ f\)

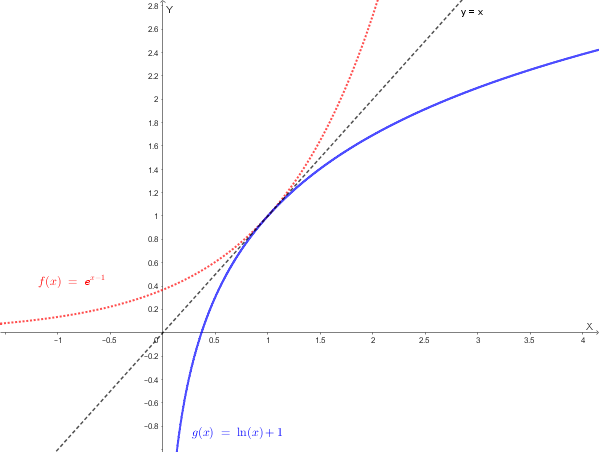
Data la funzione \(h(x) = \sqrt{x}\), il cui dominio è \(D_h = [0, +\infty)\).

1. Funzione composta \(f \circ h\):
   Si definisce \( (f \circ h)(x) = f(h(x)) \).
   Dobbiamo sostituire \(h(x)\) al posto di \(x\) nella funzione \(f(x) = e^{x-1}\).

   \[ (f \circ h)(x) = f(\sqrt{x}) = e^{\sqrt{x}-1} \]

   Per il dominio di \(f \circ h\):

   • L'argomento di \(h(x)\) deve essere nel dominio di \(h\), quindi \(x \ge 0\).
   • L'immagine di \(h(x)\) deve essere nel dominio di \(f\). Il dominio di \(f\) è \(\mathbb{R}\), e \(\sqrt{x}\) è sempre un numero reale se \(x \ge 0\). Non ci sono ulteriori restrizioni.

   Pertanto, il dominio di \(f \circ h\) è \([0, +\infty)\).

   \[ (f \circ h)(x) = e^{\sqrt{x}-1} \quad \text{con } D_{f \circ h} = [0, +\infty) \]

2. Funzione composta \(h \circ f\):
   Si definisce \( (h \circ f)(x) = h(f(x)) \).
   Dobbiamo sostituire \(f(x)\) al posto di \(x\) nella funzione \(h(x) = \sqrt{x}\).

   \[ (h \circ f)(x) = h(e^{x-1}) = \sqrt{e^{x-1}} \]

   Per il dominio di \(h \circ f\):

   • L'argomento di \(f(x)\) deve essere nel dominio di \(f\), quindi \(x \in \mathbb{R}\).
   • L'immagine di \(f(x)\) deve essere nel dominio di \(h\). Il dominio di \(h\) è \([0, +\infty)\), quindi dobbiamo avere \(f(x) \ge 0\). Sappiamo che \(f(x) = e^{x-1}\) è sempre strettamente positiva (\(e^{x-1} > 0\)) per ogni \(x \in \mathbb{R}\). Poiché è sempre maggiore di zero, è sempre maggiore o uguale a zero. Non ci sono quindi ulteriori restrizioni.

   Pertanto, il dominio di \(h \circ f\) è \(\mathbb{R}\).

   \[ (h \circ f)(x) = \sqrt{e^{x-1}} \quad \text{con } D_{h \circ f} = \mathbb{R} \]