



Questo compito è stato assegnato il giorno 05 Ottobre 2010 a una classe 5ª del Liceo Scientifico.
Argomenti: Proprietà degli insiemi di numeri reali (estremo inferiore e superiore, massimo e minimo di un insieme, punti di accumulazione, punti interni, punti esterni, punti di frontiera), Dominio di una funzione, Principio di induzione, Funzione inversa, Funzione composta.
Dato l'insieme di numeri reali:
\[ E=\left\{x \in \mathbb{R} \mid x=\frac{n+2}{n+1}, n \in \mathbb{N}\right\} \]
Determinare l'estremo inferiore, l'estremo superiore, eventuali massimo e minimo, eventuali punti di accumulazione, eventuali punti isolati, i punti interni, i punti esterni e la frontiera di E.
Per determinare le proprietà richieste dell'insieme \(E\), dobbiamo prima analizzare la funzione che genera i suoi elementi:
\[ x_n = \frac{n+2}{n+1} \]
dove \(n\) appartiene all'insieme dei numeri naturali \(\mathbb{N}\), che include lo zero. Quindi \(n \in \{0, 1, 2, 3, \dots\}\).
Analizziamo l'andamento di \(x_n\) per i primi valori di \(n\):
Possiamo riscrivere \(x_n\) in una forma più utile per l'analisi del limite:
\[ x_n = \frac{n+1+1}{n+1} = 1 + \frac{1}{n+1} \]
All'aumentare di \(n\), il termine \(\frac{1}{n+1}\) diminuisce e si avvicina a 0. Di conseguenza, il valore di \(x_n\) diminuisce e si avvicina a 1. L'insieme \(E\) è quindi composto da punti che si accumulano attorno a 1.
L'insieme \(E\) è l'insieme dei valori che la funzione assume per \(n \in \mathbb{N}\) (inclusi i numeri naturali), ovvero: \(E = \left\{2, \frac{3}{2}, \frac{4}{3}, \frac{5}{4}, \dots\right\}\).
Estremo superiore (sup E): Il valore più grande che la funzione assume si ha per il più piccolo valore di \(n\), cioè \(n=0\).
\[ \text{sup } E = x_0 = 2 \]
Massimo (max E): Poiché il valore \(2\) è effettivamente un elemento dell'insieme \(E\) (per \(n=0\)), allora \(2\) è il **massimo** di \(E\).
\[ \text{max } E = 2 \]
Estremo inferiore (inf E): Quando \(n \to \infty\), il valore di \(x_n\) tende a 1. Questo significa che 1 è il più grande dei minoranti dell'insieme \(E\).
\[ \text{inf } E = 1 \]
Minimo (min E): Poiché la funzione \(x_n = 1 + \frac{1}{n+1}\) non è mai uguale a 1, l'insieme **non ha minimo**. Il valore 1 è un punto di accumulazione ma non appartiene all'insieme.
Punti di accumulazione: L'unico valore a cui si "accumulano" gli elementi dell'insieme è 1. Qualunque intorno di 1 conterrà infiniti elementi di \(E\).
\[ \text{Punti di accumulazione di } E = \{1\} \]
Punti isolati: Un punto è isolato se esiste un intorno che non contiene altri punti dell'insieme. Tutti gli elementi dell'insieme \(E\) sono **punti isolati**, perché sono valori discreti che si avvicinano a 1 senza toccarlo.
\[ \text{Punti isolati di } E = E = \left\{1+\frac{1}{n+1} \mid n \in \mathbb{N}\right\} \]
Punti interni: Un punto è interno se esiste un intorno che è interamente contenuto nell'insieme. Poiché \(E\) è un insieme di punti discreti, non esistono intorni che contengano solo punti di \(E\). Pertanto, **l'insieme dei punti interni di \(E\) è vuoto** (\(\emptyset\)).
\[ \text{Int}(E) = \emptyset \]
Punti esterni: Un punto è esterno se ha un intorno che non interseca \(E\). Tutti i numeri reali che non sono né in \(E\) né il punto di accumulazione \(1\) sono punti esterni.
\[ \text{Est}(E) = \mathbb{R} \setminus (E \cup \{1\}) \]
Frontiera di E: La frontiera di un insieme è l'insieme dei punti che non sono né interni né esterni. In questo caso, la frontiera di \(E\) è l'unione dei punti di accumulazione e dei punti isolati di \(E\). Essa coincide con la **chiusura dell'insieme E**, \(\overline{E}\).
\[ \overline{E} = E \cup \{1\} = \left\{1+\frac{1}{n+1} \mid n \in \mathbb{N}\right\} \cup \{1\} \]
I valori di \( x_n \) possono essere visti come le ordinate dei punti della funzione \(f(x)=\frac{x+2}{x+1}\), che è un'iperbole equilatera traslata, quando la x assume i valori naturali \(x=0, x=1, x=2, x=3, \text{ etc.}\).
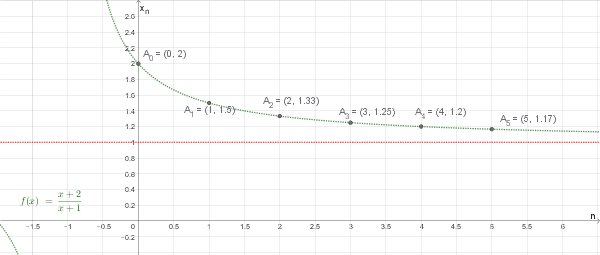
Osservando il grafico si vede bene che i punti \(x_n\) sono isolati, che \(2\) è il massimo (e quindi anche l'estremo superiore), che i valori tendono ad \(1\), che è l'estremo inferiore (ma non minimo) ed anche punto di accumulazione.
Trovare l'insieme di definizione (o dominio) della funzione di equazione: \[ y=f(x)=\frac{\sqrt{x-3}}{\ln(x^2+4x-5)} \]
Per trovare il dominio della funzione \( y=f(x)=\frac{\sqrt{x-3}}{\ln(x^2+4x-5)} \), dobbiamo imporre le condizioni di esistenza per ogni sua componente, tenendo conto che il denominatore non può essere zero.
Le condizioni sono le seguenti:
Condizione sulla radice quadrata: Il radicando deve essere maggiore o uguale a zero.
\[ x-3 \ge 0 \implies x \ge 3 \]
Condizione sul logaritmo naturale: L'argomento del logaritmo deve essere strettamente maggiore di zero.
\[ x^2+4x-5 > 0 \]
Per risolvere questa disequazione, cerchiamo le radici dell'equazione \(x^2+4x-5=0\). Utilizzando la formula risolutiva:
\[ x = \frac{-4 \pm \sqrt{4^2 - 4(1)(-5)}}{2} = \frac{-4 \pm \sqrt{16+20}}{2} = \frac{-4 \pm \sqrt{36}}{2} = \frac{-4 \pm 6}{2} \]
Le due radici sono \(x_1=\frac{-4-6}{2}=-5\) e \(x_2=\frac{-4+6}{2}=1\). Poiché il coefficiente di \(x^2\) è positivo (\(a>0\)), la disequazione è verificata per valori esterni alle radici.
\[ x < -5 \lor x > 1 \]
Condizione sul denominatore: Il denominatore della frazione non può essere zero.
\[ \ln(x^2+4x-5) \ne 0 \]
Questa condizione è vera quando l'argomento del logaritmo è diverso da 1.
\[ x^2+4x-5 \ne 1 \implies x^2+4x-6 \ne 0 \]
Troviamo le radici di \(x^2+4x-6=0\):
\[ x = \frac{-4 \pm \sqrt{4^2 - 4(1)(-6)}}{2} = \frac{-4 \pm \sqrt{16+24}}{2} = \frac{-4 \pm \sqrt{40}}{2} = \frac{-4 \pm 2\sqrt{10}}{2} = -2 \pm \sqrt{10} \]
Quindi, i valori da escludere sono \(x \ne -2 - \sqrt{10}\) e \(x \ne -2 + \sqrt{10}\). Notiamo che \(-2 - \sqrt{10} \approx -5.16\) e \(-2 + \sqrt{10} \approx 1.16\).
Ora dobbiamo combinare tutte le condizioni con un sistema, usando un grafico per visualizzare le intersezioni:
Dall'analisi delle tre condizioni, vediamo che l'unica regione in cui sono tutte verificate contemporaneamente è \(x \ge 3\). L'intervallo \((-\infty, -5)\) viene escluso dalla prima condizione (\(x \ge 3\)). Il valore \(x=-2-\sqrt{10}\) non rientra nell'intervallo finale. Il valore \(x=-2+\sqrt{10} \approx 1.16\) non rientra nell'intervallo \(x \ge 3\), quindi l'unica esclusione rilevante è per \(x \ge 3\).
Il valore \(x=-2+\sqrt{10} \approx 1.16\) si trova tra 1 e 3, ma l'intervallo \([3, +\infty)\) è l'unica parte che ci interessa. Quindi, la condizione \(x \ne -2+\sqrt{10}\) non incide sulla soluzione finale.
L'insieme di definizione (dominio) della funzione è pertanto:
\[ D = [3, +\infty) \]
Dimostrare prima per via diretta e poi per induzione che \(5^{2n}-3^{2n}\) è un numero pari per ogni numero naturale \(n\).
Vogliamo dimostrare che l'espressione \(5^{2n}-3^{2n}\) è un numero pari per ogni numero naturale \(n\).
L'espressione può essere riscritta come \((5^2)^n - (3^2)^n\), che è uguale a \(25^n - 9^n\).
Possiamo applicare la formula di scomposizione della differenza di potenze \(a^n-b^n = (a-b)(a^{n-1} + a^{n-2}b + \dots + b^{n-1})\).
Nel nostro caso, abbiamo \(a=25\) e \(b=9\). Quindi:
\[ 25^n - 9^n = (25-9)(25^{n-1} + 25^{n-2} \cdot 9 + \dots + 9^{n-1}) \]
Semplificando il primo fattore, otteniamo:
\[ 25^n - 9^n = 16 \cdot (25^{n-1} + 25^{n-2} \cdot 9 + \dots + 9^{n-1}) \]
Poiché uno dei fattori è \(16\), che è un numero pari, l'intera espressione è un multiplo di 16 e quindi è un numero pari. La dimostrazione è completa.
Vogliamo dimostrare che \(P(n): 5^{2n}-3^{2n}\) è un numero pari per ogni \(n \in \mathbb{N}\).
Per \(n=0\), l'espressione diventa:
\[ 5^{2 \cdot 0} - 3^{2 \cdot 0} = 5^0 - 3^0 = 1-1 = 0 \]
Il numero \(0\) è un numero pari, quindi il passo base è verificato.
Assumiamo che \(P(n)\) sia vera, cioè che \(5^{2n}-3^{2n}\) sia un numero pari per un certo \(n \in \mathbb{N}\). Questo significa che \(5^{2n}-3^{2n} = 2m\) per qualche intero \(m\).
Da questa ipotesi, possiamo ricavare un'espressione per \(5^{2n}\):
\[ 5^{2n} = 3^{2n} + 2m \]
Ora dobbiamo dimostrare che anche \(P(n+1)\) è vera, cioè che \(5^{2(n+1)}-3^{2(n+1)}\) è un numero pari.
Partiamo dall'espressione per \(P(n+1)\):
\[ 5^{2(n+1)}-3^{2(n+1)} = 5^{2n+2}-3^{2n+2} = 5^{2n} \cdot 5^2 - 3^{2n} \cdot 3^2 = 25 \cdot 5^{2n} - 9 \cdot 3^{2n} \]
Sostituiamo \(5^{2n}\) con l'espressione ricavata dall'ipotesi induttiva (\(3^{2n} + 2m\)):
\[ = 25 \cdot (3^{2n} + 2m) - 9 \cdot 3^{2n} \]
Sviluppiamo l'espressione:
\[ = 25 \cdot 3^{2n} + 50m - 9 \cdot 3^{2n} \]
Raggruppiamo i termini con \(3^{2n}\):
\[ = (25-9) \cdot 3^{2n} + 50m \]
\[ = 16 \cdot 3^{2n} + 50m \]
Mettiamo in evidenza il fattore 2:
\[ = 2(8 \cdot 3^{2n} + 25m) \]
Poiché l'espressione è un multiplo di 2, è un numero pari. La dimostrazione è completa.
La funzione data è \(y=f(x)=e^{x+1}\).
Dominio: L'esponente \(x+1\) non ha restrizioni, in quanto è un polinomio. La funzione esponenziale \(e^z\) è definita per tutti i valori reali di \(z\). Pertanto, il dominio di \(f(x)\) è l'intero insieme dei numeri reali.
\[ D_f = \mathbb{R} \]
Grafico: Il grafico di \(y=e^{x+1}\) si ottiene dal grafico della funzione base \(y=e^x\) tramite una traslazione orizzontale di 1 unità verso sinistra.
Ecco il grafico della funzione:
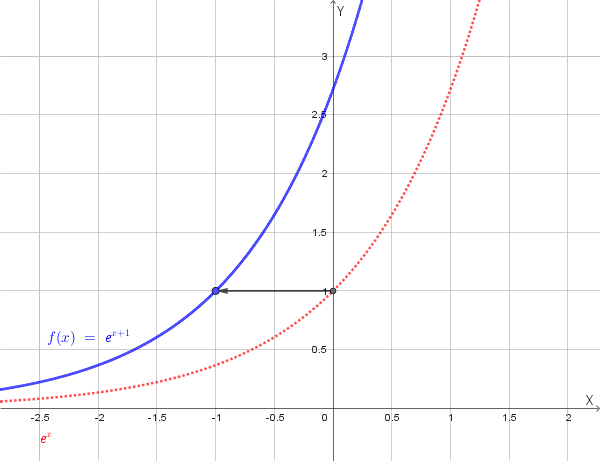
Invertibilità: La funzione è invertibile perché è strettamente crescente su tutto il suo dominio. Questo la rende una funzione biunivoca (ad ogni valore di \(x\) corrisponde un solo valore di \(y\) e viceversa) e quindi invertibile.
Funzione inversa: Per trovare l'equazione della funzione inversa, seguiamo questi passaggi:
Scrivi l'equazione della funzione: \(y = e^{x+1}\).
Scambia \(x\) con \(y\): \(x = e^{y+1}\).
Risolvi per \(y\). Applichiamo il logaritmo naturale (ln) a entrambi i lati dell'equazione:
\[ \ln(x) = \ln(e^{y+1}) \]
Usando la proprietà dei logaritmi \(\ln(e^A) = A\):
\[ \ln(x) = y+1 \]
\[ y = \ln(x) - 1 \]
La funzione inversa è \(f^{-1}(x) = \ln(x) - 1\). Il suo dominio è \((0, +\infty)\).
Grafico dell'inversa: Il grafico di \(f^{-1}(x)\) si ottiene riflettendo il grafico di \(f(x)\) rispetto alla retta \(y=x\).
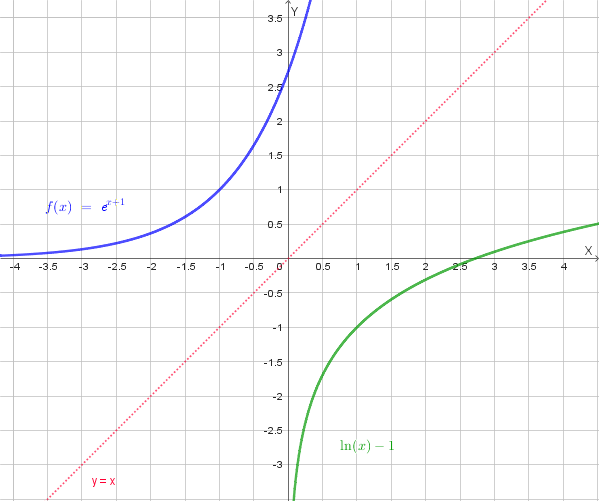
Data la funzione \(g(x) = \frac{1}{x}\), con dominio \(D_g = \mathbb{R} \setminus \{0\}\).
Funzione composta \(f \circ g\):
Si definisce \( (f \circ g)(x) = f(g(x)) \). Dobbiamo sostituire \(g(x)\) al posto di \(x\) nella funzione \(f(x) = e^{x+1}\).
\[ (f \circ g)(x) = f\left(\frac{1}{x}\right) = e^{\frac{1}{x}+1} \]
Dominio: Il dominio di \(f \circ g\) è l'insieme dei valori di \(x\) che sono nel dominio di \(g\) e per cui \(g(x)\) è nel dominio di \(f\).
Pertanto, il dominio di \(f \circ g\) è \( \mathbb{R} \setminus \{0\} \).
\[ (f \circ g)(x) = e^{\frac{1}{x}+1} \quad \text{con } D_{f \circ g} = \mathbb{R} \setminus \{0\} \]
Funzione composta \(g \circ f\):
Si definisce \( (g \circ f)(x) = g(f(x)) \). Dobbiamo sostituire \(f(x)\) al posto di \(x\) nella funzione \(g(x) = \frac{1}{x}\).
\[ (g \circ f)(x) = g(e^{x+1}) = \frac{1}{e^{x+1}} \]
Dominio: Il dominio di \(g \circ f\) è l'insieme dei valori di \(x\) che sono nel dominio di \(f\) e per cui \(f(x)\) è nel dominio di \(g\).
Pertanto, non ci sono restrizioni e il dominio di \(g \circ f\) è \(\mathbb{R}\).
\[ (g \circ f)(x) = \frac{1}{e^{x+1}} \quad \text{con } D_{g \circ f} = \mathbb{R} \]
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.