Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
Per un ripasso sulla teoria degli Asintoti di una funzione visita la seguente pagina pubblicata sul "vecchio" sito di Matefilia>


Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
Per un ripasso sulla teoria degli Asintoti di una funzione visita la seguente pagina pubblicata sul "vecchio" sito di Matefilia>
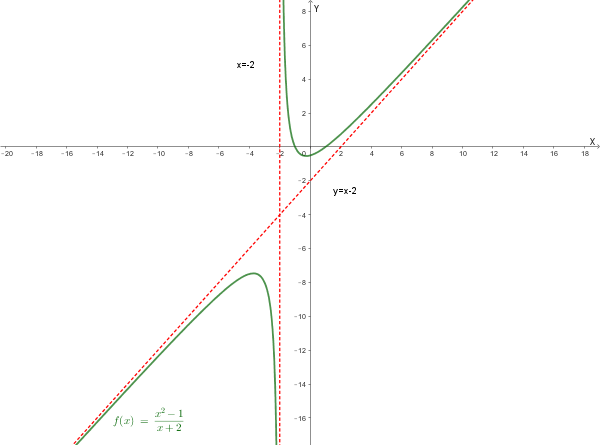
Dopo aver trovato il **dominio** della seguente funzione \[ f(x) = \frac{x^2 - 1}{x + 2} \] ricerca gli eventuali **asintoti** (verticali, orizzontali e obliqui).
Soluzione quesito 1:
Per trovare il dominio della funzione (che è una funzione razionale fratta), dobbiamo porre il denominatore diverso da zero.
\[ x + 2 \ne 0 \implies x \ne -2 \]Quindi il dominio della funzione è \(D = (-\infty, -2) \cup (-2, +\infty)\).
Gli asintoti verticali possono esistere nei punti esclusi dal dominio, in questo caso in \(x = -2\). Calcoliamo il limite per \(x \to -2\):
\[ \lim_{x \to -2} \frac{x^2 - 1}{x + 2} = \frac{(-2)^2 - 1}{(-2) + 2} = \frac{4 - 1}{0} = \frac{3}{0} \]Poiché il numeratore tende a \(3\) e il denominatore tende a \(0\), il limite sarà \(\infty\). Calcoliamo i limiti laterali per determinarne il segno:
\[ \lim_{x \to -2^-} \frac{x^2 - 1}{x + 2} = \frac{3}{0^-} = -\infty \] \[ \lim_{x \to -2^+} \frac{x^2 - 1}{x + 2} = \frac{3}{0^+} = +\infty \]La retta di equazione **\(x = -2\)** è un **asintoto verticale**.
Gli asintoti orizzontali si cercano calcolando il limite della funzione per \(x \to \pm\infty\):
\[ \lim_{x \to \pm\infty} \frac{x^2 - 1}{x + 2} = \lim_{x \to \pm\infty} \frac{x^2}{x} = \lim_{x \to \pm\infty} x = \pm\infty \]Poiché il limite è infinito, **non ci sono asintoti orizzontali**.
Poiché il grado del numeratore (2) supera di uno il grado del denominatore (1) e non ci sono asintoti orizzontali, cerchiamo un asintoto obliquo di equazione \(y = mx + q\).
Calcolo di \(m\):
\[ m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \frac{x^2 - 1}{x(x + 2)} = \lim_{x \to \pm\infty} \frac{x^2 - 1}{x^2 + 2x} = \lim_{x \to \pm\infty} \frac{x^2}{x^2} = 1 \]Quindi **\(m = 1\)**.
Calcolo di \(q\):
\[ q = \lim_{x \to \pm\infty} [f(x) - mx] = \lim_{x \to \pm\infty} \left[ \frac{x^2 - 1}{x + 2} - 1 \cdot x \right] = \lim_{x \to \pm\infty} \left[ \frac{x^2 - 1 - x(x + 2)}{x + 2} \right] \] \[ q = \lim_{x \to \pm\infty} \left[ \frac{x^2 - 1 - x^2 - 2x}{x + 2} \right] = \lim_{x \to \pm\infty} \frac{-2x - 1}{x + 2} = \lim_{x \to \pm\infty} \frac{-2x}{x} = -2 \]Quindi **\(q = -2\)**.
La retta di equazione **\(y = x - 2\)** è un **asintoto obliquo** (valido sia per \(x \to +\infty\) che per \(x \to -\infty\)).
Mostriamo, anche se non richiesto, il grafico della funzione:
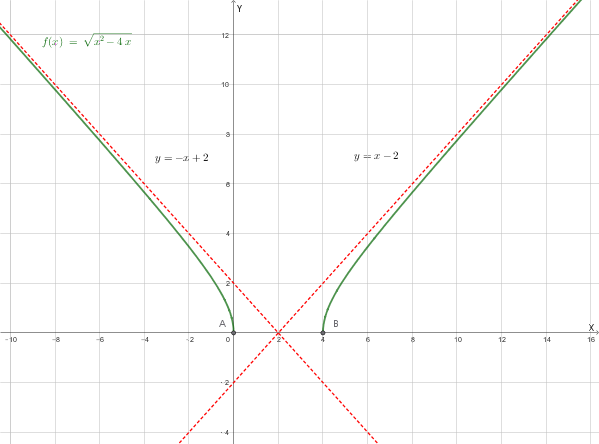
Dopo aver trovato il **dominio** della seguente funzione irrazionale \[ f(x) = \sqrt{x^2 - 4x} \] ricerca gli eventuali **asintoti** (verticali, orizzontali e obliqui).
Soluzione quesito 2:
Per trovare il dominio della funzione (che è una funzione irrazionale con radice di indice pari), dobbiamo imporre che l'argomento della radice sia maggiore o uguale a zero.
\[ x^2 - 4x \ge 0 \]Risolvendo l'equazione associata \(x^2 - 4x = 0 \implies x(x - 4) = 0\), le radici sono \(x = 0\) e \(x = 4\). Poiché la parabola ha concavità verso l'alto, la disequazione è soddisfatta per valori esterni alle radici.
Quindi il dominio della funzione è \(D = (-\infty, 0] \cup [4, +\infty)\).
**Non ci sono asintoti verticali** perché la funzione è continua nel suo dominio
Gli asintoti orizzontali si cercano calcolando il limite della funzione per \(x \to \pm\infty\):
\[ \lim_{x \to \pm\infty} \sqrt{x^2 - 4x} = \lim_{x \to \pm\infty} \sqrt{x^2} = \lim_{x \to \pm\infty} |x| = +\infty \]Poiché il limite è infinito, **non ci sono asintoti orizzontali**. Cerchiamo gli asintoti obliqui.
Cerchiamo l'asintoto obliquo \(y = mx + q\) separatamente per \(x \to +\infty\) e per \(x \to -\infty\).
Caso 1: \(x \to +\infty\) (dove \(|x| = x\))
Calcolo di \(m_1\):
\[ m_1 = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{\sqrt{x^2 - 4x}}{x} = \lim_{x \to +\infty} \frac{\sqrt{x^2(1 - 4/x)}}{x} = \lim_{x \to +\infty} \frac{x \sqrt{1 - 4/x}}{x} = 1 \]Quindi **\(m_1 = 1\)**.
Calcolo di \(q_1\):
\[ q_1 = \lim_{x \to +\infty} [f(x) - m_1 x] = \lim_{x \to +\infty} \left[ \sqrt{x^2 - 4x} - x \right] \]La forma indeterminata \(\infty - \infty\) si risolve moltiplicando e dividendo per il fattore razionalizzante:
\[ q_1 = \lim_{x \to +\infty} \frac{(\sqrt{x^2 - 4x} - x)(\sqrt{x^2 - 4x} + x)}{\sqrt{x^2 - 4x} + x} = \lim_{x \to +\infty} \frac{(x^2 - 4x) - x^2}{\sqrt{x^2 - 4x} + x} \] \[ q_1 = \lim_{x \to +\infty} \frac{-4x}{\sqrt{x^2(1 - 4/x)} + x} = \lim_{x \to +\infty} \frac{-4x}{x\sqrt{1 - 4/x} + x} = \lim_{x \to +\infty} \frac{-4x}{x(\sqrt{1 - 4/x} + 1)} \] \[ q_1 = \lim_{x \to +\infty} \frac{-4}{\sqrt{1 - 4/x} + 1} = \frac{-4}{\sqrt{1 - 0} + 1} = \frac{-4}{2} = -2 \]Quindi **\(q_1 = -2\)**. L'asintoto obliquo per \(x \to +\infty\) è **\(y = x - 2\)**.
Caso 2: \(x \to -\infty\) (dove \(|x| = -x\)
Calcolo di \(m_2\):
\[ m_2 = \lim_{x \to -\infty} \frac{f(x)}{x} = \lim_{x \to -\infty} \frac{\sqrt{x^2 - 4x}}{x} = \lim_{x \to -\infty} \frac{\sqrt{x^2(1 - 4/x)}}{x} = \lim_{x \to -\infty} \frac{|x| \sqrt{1 - 4/x}}{x} \]Poiché \(x \to -\infty\), \(|x| = -x\):
\[ m_2 = \lim_{x \to -\infty} \frac{-x \sqrt{1 - 4/x}}{x} = \lim_{x \to -\infty} - \sqrt{1 - 4/x} = -1 \]Quindi **\(m_2 = -1\)**.
Calcolo di \(q_2\):
\[ q_2 = \lim_{x \to -\infty} [f(x) - m_2 x] = \lim_{x \to -\infty} \left[ \sqrt{x^2 - 4x} - (-1)x \right] = \lim_{x \to -\infty} \left[ \sqrt{x^2 - 4x} + x \right] \]La forma indeterminata \(\infty - \infty\) si risolve moltiplicando e dividendo per il fattore razionalizzante:
\[ q_2 = \lim_{x \to -\infty} \frac{(\sqrt{x^2 - 4x} + x)(\sqrt{x^2 - 4x} - x)}{\sqrt{x^2 - 4x} - x} = \lim_{x \to -\infty} \frac{(x^2 - 4x) - x^2}{\sqrt{x^2 - 4x} - x} \] \[ q_2 = \lim_{x \to -\infty} \frac{-4x}{\sqrt{x^2(1 - 4/x)} - x} = \lim_{x \to -\infty} \frac{-4x}{|x|\sqrt{1 - 4/x} - x} \]Poiché \(x \to -\infty\), \(|x| = -x\):
\[ q_2 = \lim_{x \to -\infty} \frac{-4x}{-x\sqrt{1 - 4/x} - x} = \lim_{x \to -\infty} \frac{-4x}{-x(\sqrt{1 - 4/x} + 1)} = \lim_{x \to -\infty} \frac{4}{\sqrt{1 - 4/x} + 1} \] \[ q_2 = \frac{4}{\sqrt{1 - 0} + 1} = \frac{4}{2} = 2 \]Quindi **\(q_2 = 2\)**. L'asintoto obliquo per \(x \to -\infty\) è **\(y = -x + 2\)**.
In conclusione, la funzione ha due asintoti obliqui distinti: **\(y = x - 2\) per \(x \to +\infty\)** e **\(y = -x + 2\) per \(x \to -\infty\)**.
Mostriamo, anche se non richiesto, il grafico della funzione:
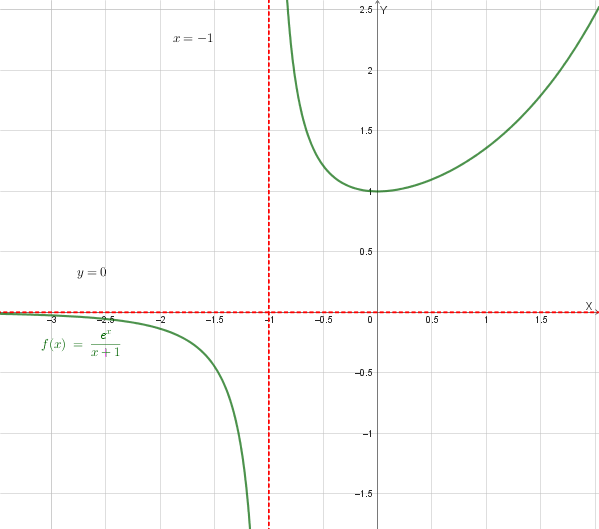
Dopo aver trovato il **dominio** della seguente funzione \[ f(x) = \frac{e^x}{x+1} \] ricerca gli eventuali **asintoti** (verticali, orizzontali e obliqui).
Soluzione quesito 3:
Per trovare il dominio della funzione, dobbiamo imporre che il denominatore sia diverso da zero.
\[ x + 1 \ne 0 \implies x \ne -1 \]Quindi il dominio della funzione è \(D = (-\infty, -1) \cup (-1, +\infty)\).
Gli asintoti verticali possono esistere nei punti esclusi dal dominio, in questo caso in \(x = -1\). Calcoliamo il limite per \(x \to -1\):
\[ \lim_{x \to -1} \frac{e^x}{x + 1} = \frac{e^{-1}}{-1 + 1} = \frac{1/e}{0} \]Poiché il numeratore tende a un valore positivo (\(1/e \approx 0.368\)) e il denominatore tende a \(0\), il limite sarà \(\infty\). Calcoliamo i limiti laterali:
\[ \lim_{x \to -1^-} \frac{e^x}{x + 1} = \frac{1/e}{0^-} = -\infty \] \[ \lim_{x \to -1^+} \frac{e^x}{x + 1} = \frac{1/e}{0^+} = +\infty \]La retta di equazione **\(x = -1\)** è un **asintoto verticale**.
Gli asintoti orizzontali si cercano calcolando il limite della funzione per \(x \to \pm\infty\).
Caso 1: \(x \to -\infty\)
\[ \lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \frac{e^x}{x + 1} = \frac{e^{-\infty}}{-\infty + 1} = \frac{0}{-\infty} = 0 \]La retta di equazione **\(y = 0\)** è un **asintoto orizzontale** per \(x \to -\infty\).
Caso 2: \(x \to +\infty\)
\[ \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \frac{e^x}{x + 1} = \frac{\infty}{\infty} \]Siccome \(e^x\) è infinito di ordine superiore rispetto a (\(x+1\)):
\[ \lim_{x \to +\infty} \frac{e^x}{x + 1} = +\infty \]Poiché il limite è infinito, **non ci sono asintoti orizzontali** per \(x \to +\infty\).
Cerchiamo l'eventuale asintoto obliquo \(y = mx + q\) per \(x \to +\infty\).
Calcolo di \(m\):
\[ m = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{e^x}{x(x + 1)} = \lim_{x \to +\infty} \frac{e^x}{x^2 + x} \]Siccome \(e^x\) è infinito di ordine superiore rispetto a (\(x^2+x\)):
\[ m = \lim_{x \to +\infty} \frac{e^x}{x^2 + x} = +\infty \]Poiché \(m\) non è finito, la funzione **non ha asintoti obliqui**.
In sintesi, la funzione ha un **asintoto verticale** \(x = -1\) e un **asintoto orizzontale** \(y = 0\) solo per \(x \to -\infty\).
Mostriamo, anche se non richiesto, il grafico della funzione:
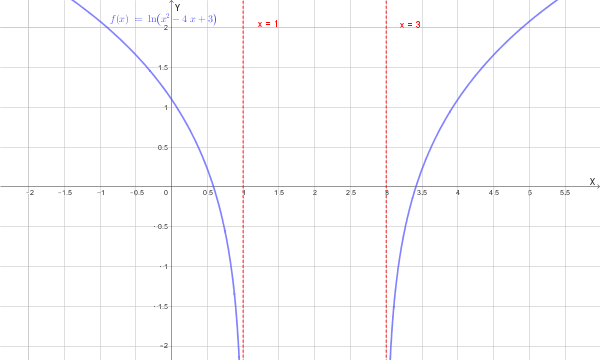
Dopo aver trovato il **dominio** della seguente funzione \[ f(x) = \ln(x^2 - 4x + 3) \] ricerca gli eventuali **asintoti** (verticali, orizzontali e obliqui).
Soluzione quesito 4:
Per trovare il **dominio** della funzione logaritmica, l'argomento deve essere strettamente positivo:
\[ x^2 - 4x + 3 > 0 \]Risolviamo l'equazione associata \(x^2 - 4x + 3 = 0\), le cui radici sono \(x_1 = 1\) e \(x_2 = 3\).
La disequazione è soddisfatta per valori esterni alle radici.
Il **dominio** della funzione è \(D = (-\infty, 1) \cup (3, +\infty)\).
Asintoti Verticali
Gli asintoti verticali vanno cercati nei punti esclusi dal dominio, ovvero \(x = 1\) e \(x = 3\). Calcoliamo i limiti laterali in questi punti. Poiché in entrambi i casi l'argomento del logaritmo tende a \(0^+\), il limite sarà \(-\infty\).
\[ \lim_{x \to 1^-} \ln(x^2 - 4x + 3) = \lim_{t \to 0^+} \ln(t) = -\infty \] \[ \lim_{x \to 3^+} \ln(x^2 - 4x + 3) = \lim_{t \to 0^+} \ln(t) = -\infty \]Le rette di equazione **\(x = 1\)** e **\(x = 3\)** sono **asintoti verticali**.
Asintoti Orizzontali
Si cercano calcolando il limite per \(x \to \pm\infty\):
\[ \lim_{x \to \pm\infty} f(x) = \lim_{x \to \pm\infty} \ln(x^2 - 4x + 3) \]Poiché per \(x \to \pm\infty\) l'argomento del logaritmo, \(x^2 - 4x + 3\), tende a \(+\infty\):
\[ \lim_{x \to \pm\infty} f(x) = \ln(+\infty) = +\infty \]Poiché il limite è infinito, **non esistono asintoti orizzontali**.
Asintoti Obliqui
L'asintoto obliquo \(y = mx + q\) si cerca per \(x \to \pm\infty\).
Calcoliamo il coefficiente angolare \(m\):
\[ m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \frac{\ln(x^2 - 4x + 3)}{x} \]Si tratta di una forma indeterminata \(\frac{\infty}{\infty}\). Siccome \(x\) è infinito di ordine superiore rispetto a \(ln(x^2 - 4x + 3) \) si ha \(m=0\).
Poiché \(m=0\), **non esistono asintoti obliqui**.
Mostriamo, anche se non richiesto, il grafico della funzione:
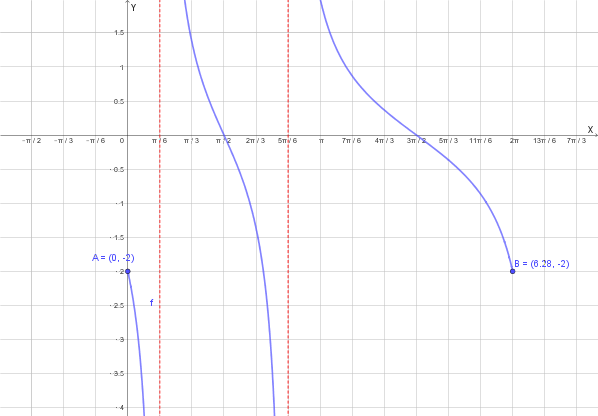
Dopo aver trovato il **dominio** della seguente funzione **nell'intervallo \([0, 2\pi]\)** \[ f(x) = \frac{\cos(x)}{\sin(x) - \frac{1}{2}} \] ricerca gli eventuali **asintoti** .
Soluzione quesito 5:
Il dominio della funzione è dato dalla condizione che il denominatore non sia nullo:
\[ \sin(x) - \frac{1}{2} \ne 0 \implies \sin(x) \ne \frac{1}{2} \]Nell'intervallo \([0, 2\pi]\), il seno è uguale a \(\frac{1}{2}\) per due valori:
\[ x = \frac{\pi}{6} \quad \text{e} \quad x = \frac{5\pi}{6} \]Il **dominio** \(D\) è l'intervallo chiuso dato, con l'esclusione di questi due punti:
\[ D = \left[0, \frac{\pi}{6}\right) \cup \left(\frac{\pi}{6}, \frac{5\pi}{6}\right) \cup \left(\frac{5\pi}{6}, 2\pi\right] \]Gli asintoti verticali si cercano nei punti di discontinuità, che in questo caso sono \(x = \frac{\pi}{6}\) e \(x = \frac{5\pi}{6}\). Calcoliamo i limiti laterali in questi punti.
1. Asintoto in \(x = \frac{\pi}{6}\)
Il numeratore in \(x = \frac{\pi}{6}\) è \(\cos(\frac{\pi}{6}) = \frac{\sqrt{3}}{2} > 0\). Il denominatore tende a \(0\).
La retta di equazione **\(x = \frac{\pi}{6}\)** è un **asintoto verticale**.
2. Asintoto in \(x = \frac{5\pi}{6}\)
Il numeratore in \(x = \frac{5\pi}{6}\) è \(\cos(\frac{5\pi}{6}) = -\frac{\sqrt{3}}{2} < 0\). Il denominatore tende a \(0\).
La retta di equazione **\(x = \frac{5\pi}{6}\)** è un **asintoto verticale**.
Asintoti Orizzontali e Obliqui
Poiché la funzione è studiata in un intervallo chiuso e limitato \([0, 2\pi]\), non ha senso calcolare limiti per \(x \to \pm\infty\). Di conseguenza, **non esistono asintoti orizzontali né obliqui** nell'intervallo di studio.
Mostriamo, anche se non richiesto, il grafico della funzione:
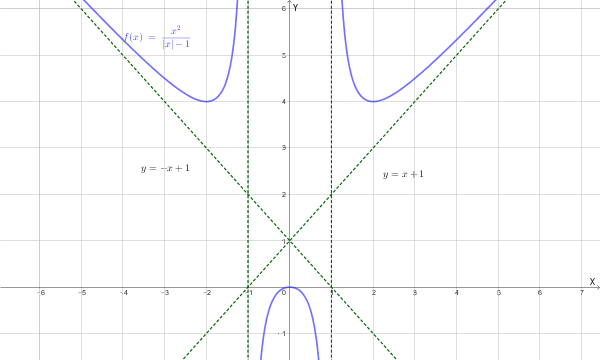
Dopo aver trovato il **dominio** della seguente funzione \[ f(x) = \frac{x^2}{|x|-1} \] ricerca gli eventuali **asintoti** (verticali, orizzontali e obliqui).
Soluzione quesito 6:
Per trovare il **dominio** della funzione, dobbiamo porre il denominatore diverso da zero:
\[ |x|-1 \ne 0 \implies |x| \ne 1 \]Questa condizione è soddisfatta per \(x \ne 1\) e \(x \ne -1\). Il **dominio** è pertanto:
\[ D = \mathbb{R} \setminus \{-1, 1\} = (-\infty, -1) \cup (-1, 1) \cup (1, +\infty) \]Per la ricerca degli asintoti, riscriviamo la funzione a tratti eliminando il valore assoluto:
\[ f(x) = \begin{cases} \frac{x^2}{x-1} & \text{se } x > 0 \quad (x \ne 1) \\ \frac{x^2}{-x-1} = -\frac{x^2}{x+1} & \text{se } x < 0 \quad (x \ne -1) \end{cases} \]Asintoti Verticali
Gli asintoti verticali vanno cercati nei punti esclusi dal dominio, \(x = 1\) e \(x = -1\).
La retta **\(x = 1\)** è un **asintoto verticale**.
La retta **\(x = -1\)** è un **asintoto verticale**.
Asintoti Orizzontali
Si cercano per \(x \to \pm\infty\). Poiché il grado del numeratore (\(2\)) è maggiore del grado del denominatore (\(1\)) in entrambi i rami, il limite sarà \(\infty\). **Non esistono asintoti orizzontali**.
Asintoti Obliqui
Osserviamo che il sia per x < 0 che per x>0 la funzione è una funzione razionale fratta in cui il grado del numeratore supera di 1 il grado del denominatiore. Quindi, per una nota proprietà, ci sarà asintoto obliquo sia per \(x \to -\infty\) sia per \(x \to +\infty\)
Ricerca deglia sintoti per \(x \to +\infty\) e \(x \to -\infty\):
1. Per \(x \to +\infty\) (Funzione: \(f(x) = \frac{x^2}{x-1}\))
La retta **\(y = x + 1\)** è un **asintoto obliquo** per \(x \to +\infty\).
2. Per \(x \to -\infty\) (Funzione: \(f(x) = -\frac{x^2}{x+1}\))
La retta **\(y = -x + 1\)** è un **asintoto obliquo** per \(x \to -\infty\).
Mostriamo, anche se non richiesto, il grafico della funzione:
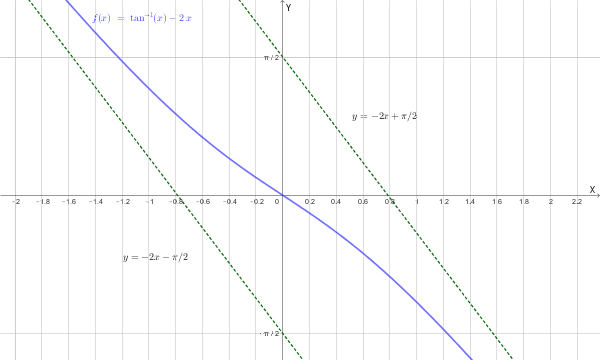
Dopo aver trovato il **dominio** della seguente funzione \[ f(x) = \arctan(x) - 2x \] ricerca gli eventuali **asintoti** (verticali, orizzontali e obliqui).
Soluzione quesito 7:
La funzione arcotangente, \(\arctan(x)\), è definita per ogni numero reale, e la funzione \(2x\) (un polinomio) è anch'essa definita per ogni numero reale. La funzione \(f(x)\), essendo la differenza di due funzioni definite su \(\mathbb{R}\), è definita ovunque.
Il **dominio** è l'insieme di tutti i numeri reali: \(D = \mathbb{R}\).
Asintoti Verticali
Poiché il dominio è \(D = \mathbb{R}\) e la funzione è continua su tutto l'asse reale (diferenza di funzioni continue) **non esistono asintoti verticali**.
Asintoti Orizzontali
Si cercano calcolando i limiti per \(x \to \pm\infty\):
Poiché i limiti tendono a \(\pm\infty\), **non esistono asintoti orizzontali**.
Asintoti Obliqui
L'asintoto obliquo \(y = mx + q\) si cerca per \(x \to \pm\infty\).
1. Coefficiente angolare \(m\)
\[ m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \frac{\arctan(x) - 2x}{x} = \lim_{x \to \pm\infty} \left( \frac{\arctan(x)}{x} - 2 \right) \]Poiché l'arcotangente è limitata (\(-\frac{\pi}{2} < \arctan(x) < \frac{\pi}{2}\)), il termine \(\frac{\arctan(x)}{x}\) tende a \(0\) per \(x \to \pm\infty\).
\[ m = 0 - 2 = -2 \]2. Intercetta \(q\)
\[ q = \lim_{x \to \pm\infty} [f(x) - mx] = \lim_{x \to \pm\infty} [(\arctan(x) - 2x) - (-2)x] \] \[ q = \lim_{x \to \pm\infty} [\arctan(x) - 2x + 2x] = \lim_{x \to \pm\infty} \arctan(x) \]Calcoliamo i limiti separatamente:
La funzione ammette due asintoti obliqui distinti, uno per \(x \to +\infty\) e uno per \(x \to -\infty\).
Mostriamo, anche se non richiesto, il grafico della funzione:
Determina i parametri \(a\) e \(b\) in modo che la funzione
\[
f(x) = \frac{ax^3 + bx^2 + 4}{x^2 - 4}
\]
abbia per asintoto obliquo la retta \(y = 2x - 1\).
In corrispondenza dei valori di \(a\) e \(b\) trovati, ricerca gli eventuali altri asintoti (verticali e orizzontali).
Soluzione quesito 8:
L'asintoto obliquo richiesto è \(y = 2x - 1\), quindi dobbiamo imporre che il coefficiente angolare sia \(m = 2\) e l'intercetta sia \(q = -1\).
1. Coefficiente angolare (\(m\))
Il coefficiente angolare \(m\) è dato dal limite del rapporto \(f(x)/x\):
\[ m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \frac{ax^3 + bx^2 + 4}{x(x^2 - 4)} = \lim_{x \to \pm\infty} \frac{ax^3}{x^3} = a \]Imponendo \(m = 2\), si ottiene: \(\mathbf{a = 2}\).
2. Intercetta (\(q\))
Sostituendo \(a=2\) e \(m=2\) nella formula per \(q\):
\[ q = \lim_{x \to \pm\infty} [f(x) - 2x] = \lim_{x \to \pm\infty} \left[ \frac{2x^3 + bx^2 + 4}{x^2 - 4} - 2x \right] \]Eseguiamo la sottrazione algebrica:
\[ q = \lim_{x \to \pm\infty} \frac{(2x^3 + bx^2 + 4) - 2x(x^2 - 4)}{x^2 - 4} = \lim_{x \to \pm\infty} \frac{2x^3 + bx^2 + 4 - 2x^3 + 8x}{x^2 - 4} \] \[ q = \lim_{x \to \pm\infty} \frac{bx^2 + 8x + 4}{x^2 - 4} \]Poiché il grado del numeratore e del denominatore è uguale (entrambi 2), il limite è dato dal rapporto dei coefficienti dei termini di grado massimo:
\[ q = \frac{b}{1} = b \]Imponendo \(q = -1\), si ottiene: \(\mathbf{b = -1}\).
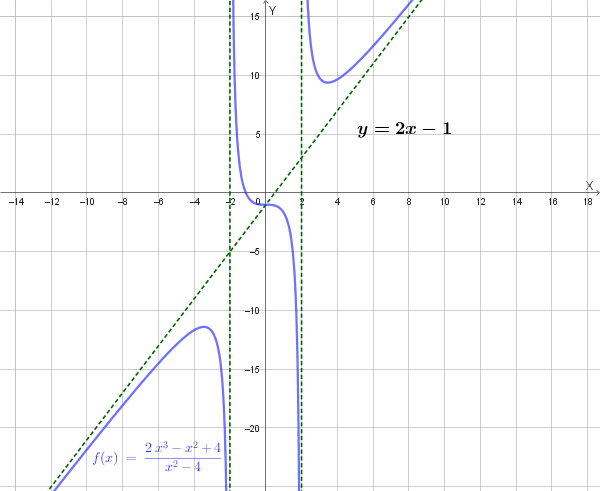
La funzione con i parametri trovati è: \[ f(x) = \frac{2x^3 - x^2 + 4}{x^2 - 4} \]
Asintoti Verticali
Gli asintoti verticali si cercano nei punti che annullano il denominatore: \(x^2 - 4 = 0 \implies x = \pm 2\). Verifichiamo il valore del numeratore \(N(x) = 2x^3 - x^2 + 4\) in questi punti.
Poiché il numeratore non si annulla, la retta **\(x = 2\)** è un **asintoto verticale**.
Poiché il numeratore non si annulla, la retta **\(x = -2\)** è un **asintoto verticale**.
Asintoti Orizzontali
Si cercano calcolando il limite per \(x \to \pm\infty\). Poiché il grado del numeratore è maggiore del grado del denominatore (\(3 > 2\)), il limite è \(\infty\).
\[ \lim_{x \to \pm\infty} f(x) = \pm\infty \]Quindi, **non esistono asintoti orizzontali**.
Mostriamo, anche se non richiesto, il grafico della funzione:
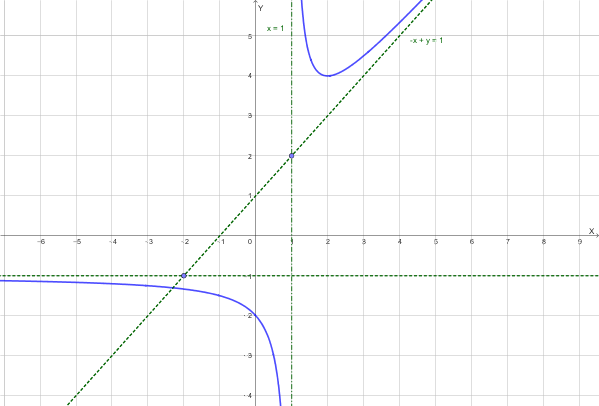
Trova l'equazione di una funzione \(f(x)\) che abbia i seguenti asintoti:
Dopo aver indicato la funzione, verifica che abbia effettivamente gli asintoti richiesti.
Soluzione quesito 9:
Per soddisfare tutte le condizioni, la funzione viene definita a tratti per gestire i diversi limiti asintotici a \(\pm\infty\) attorno all'asintoto verticale in \(x=1\):
\[ \mathbf{f(x) = \begin{cases} \frac{x}{x - 1} - 2 & \text{se } x < 1 \\ (x+1)+\frac{1}{x - 1} & \text{se } x > 1 \end{cases}} \]1. Asintoto Verticale (\(x = 1\))
La retta \(\mathbf{x = 1}\) è un **asintoto verticale**.
2. Asintoto Orizzontale a sinistra (\(y = -1\) per \(x \to -\infty\))
Usiamo la prima espressione:
\[ \lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \left( \frac{x}{x - 1} - 2 \right) \]Poiché \(\frac{x}{x - 1} = 1 + \frac{1}{x - 1}\) e per \(x \to -\infty\) il termine \(\frac{1}{x - 1}\) è negativo, si ha che \(\frac{x}{x-1}\) tende a \(1^-\) (cioè è minore di 1).
\[ = (1^-) - 2 = -1^- \]La retta \(\mathbf{y = -1}\) è l'**asintoto orizzontale a sinistra**.
3. Asintoto Obliquo a destra (\(y = x + 1\) per \(x \to +\infty\))
In base ad una proprietà dimostrata nella pagina sugli asintoti citata nel sottotitolo, essendo la funzione nella forma \( f(x)=mx+q+g(x) \) con \( g(x) \) infinitesimo per \(x \to +\infty\), la retta \(y=x+1 \) è asintoto per \(x \to +\infty\).
Facciamo una dimostrazione diretta.
Usando \(f(x) = (x+1)+\frac{1}{x - 1}\) per \(x \to +\infty\), si trova:
La retta \(\mathbf{y = x + 1}\) è l'**asintoto obliquo a destra**.
Il grafico presenta tre rami principali definiti dai suoi asintoti:
Dimostra che se una funzione può essere espressa nella forma
\[
f(x) = mx + q + g(x)
\]
con \(g(x)\) infinitesimo per \(x \to \pm\infty\) (ovvero \(\lim_{x \to \pm\infty} g(x) = 0\)), allora la retta \(y = mx + q\) è **asintoto obliquo** (o orizzontale) per la funzione \(f(x)\).
Fornisci un esempio e verifica quanto dimostrato in generale.
Soluzione quesito 10:
Per definizione, la retta \(y = mx + q\) è un asintoto per una curva se la distanza di un generico punto P della curva dalla retta tende a zero quando P si allontana indefinitamente sulla curva.
Osserviamo la seguente figura:
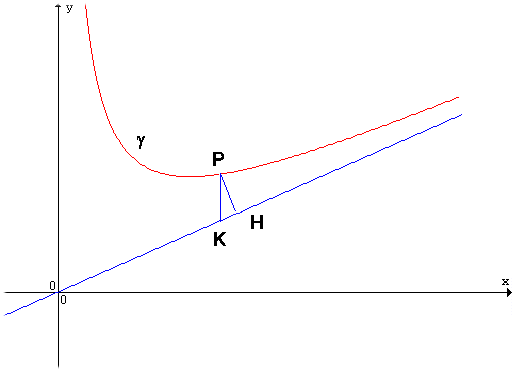
Per definizione di asintoto, la retta r è asintoto per la funzione se PH tende a 0. Verifichiamo che PK tende a zero per \(x \to \pm\infty\):
\[ \lim_{x \to \pm\infty} [f(x) - (mx + q)] = 0 \]Sostituendo l'espressione data \(f(x) = mx + q + g(x)\) nella condizione limite:
\[ \lim_{x \to \pm\infty} [f(x) - (mx + q)] = \lim_{x \to \pm\infty} [(mx + q + g(x)) - (mx + q)] = \lim_{x \to \pm\infty} g(x) \]Per ipotesi, \(\lim_{x \to \pm\infty} g(x) = 0\). Quindi: \(\lim_{x \to \pm\infty} [f(x) - (mx + q)] = 0\).
Ciò vuol dire che PK tende a 0. Ma se tende a 0 PK, tende a 0 anche PH, essendo PH < PK, perciò:
**\(y = mx + q\) è asintoto**.
Osserviamo la seguente figura:
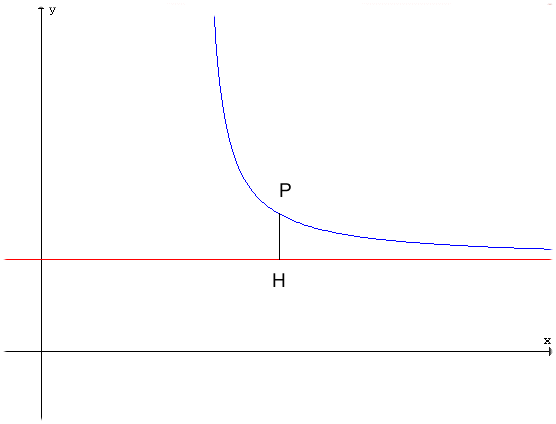
Per definizione di asintoto, la retta r è asintoto per la funzione se PH tende a 0 per \(x \to \pm\infty\):
Verifichiamo che PH tende a zero per \(x \to \pm\infty\)
Risulta:
PH=(f(x) - (mx + q))Abbiamo:
\[ \lim_{x \to \pm\infty} [f(x) - (mx + q)] =\lim_{x \to \pm\infty} g(x)= 0 \]Questo dimostra che se \(m=0\), la retta \(\mathbf{y = q}\) è l'asintoto orizzontale.
Se \(m=0\), la retta asintotica è \(y = q\). La funzione diventa \(f(x) = q + g(x)\).
Calcoliamo il limite della funzione per \(x \to \pm\infty\):
Poiché \(q\) è una costante e \(\lim_{x \to \pm\infty} g(x) = 0\) per ipotesi, otteniamo:
\[ \lim_{x \to \pm\infty} f(x) = q + 0 = q \]Questo dimostra che se \(m=0\), la retta \(\mathbf{y = q}\) è l'asintoto orizzontale.
Se \(m \ne 0\), la retta è \(y = mx + q\). Per dimostrare che è un asintoto obliquo, dobbiamo verificare che le condizioni di esistenza (incluso il fatto che la funzione tenda a \(\infty\)) siano soddisfatte:
a) La funzione tende a \(\infty\):
\[ \lim_{x \to \pm\infty} f(x) = \lim_{x \to \pm\infty} [mx + q + g(x)] = \pm\infty + q + 0 = \pm\infty \]b) Il coefficiente angolare è \(m\):
Calcoliamo il limite del rapporto \(\frac{f(x)}{x}\):
\[ \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \frac{mx + q + g(x)}{x} = \lim_{x \to \pm\infty} \left( m + \frac{q}{x} + \frac{g(x)}{x} \right) \]Poiché \(\lim_{x \to \pm\infty} \frac{q}{x} = 0\) e \(\lim_{x \to \pm\infty} \frac{g(x)}{x} = 0\) (essendo \(g(x)\) infinitesima, lo è ancora di più se divisa per \(x\)), si ottiene:
\[ \lim_{x \to \pm\infty} \frac{f(x)}{x} = m + 0 + 0 = m \]c) Il limite della differenza è \( q\):
Il limite della differenza tra \( f(x)-mx \) è: \[ \lim_{x \to \pm\infty} [f(x) - mx] =\lim_{x \to \pm\infty} [q+g(x)]=q+0= q \]
Questo conferma che la retta \(\mathbf{y = mx + q}\) è asintoto obliquo per \(f(x)\).
Consideriamo la funzione \(f(x)\) e verifichiamo la condizione \(f(x) = mx + q + g(x)\).
Consideriamo la funzione \(f(x) = 2 + \frac{1}{x}\) per \(x \to \pm\infty\).
In questo caso, la funzione è già nella forma \(f(x) = mx + q + g(x)\) con:
Verifichiamo che \(g(x)\) sia infinitesimo per \(x \to \pm\infty\):
\[ \lim_{x \to \pm\infty} g(x) = \lim_{x \to \pm\infty} \frac{1}{x} = 0 \]La dimostrazione garantisce che la retta \(\mathbf{y = 2}\) è l'asintoto. Verifichiamo direttamente l'asintoto orizzontale:
\[ \lim_{x \to \pm\infty} f(x) = \lim_{x \to \pm\infty} \left( 2 + \frac{1}{x} \right) = 2 + 0 = 2 \]Poiché il limite è \(2\), la retta \(\mathbf{y = 2}\) è l'asintoto orizzontale per la funzione.
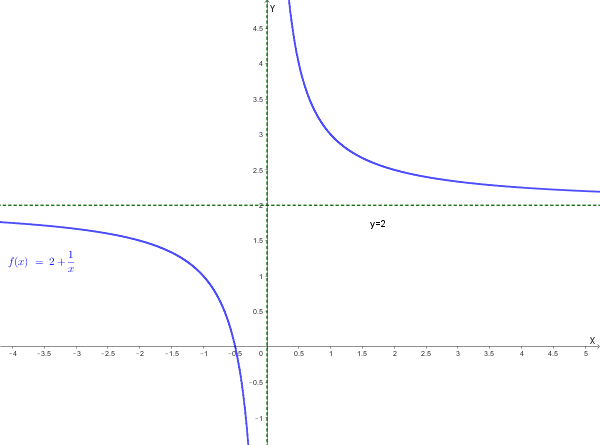
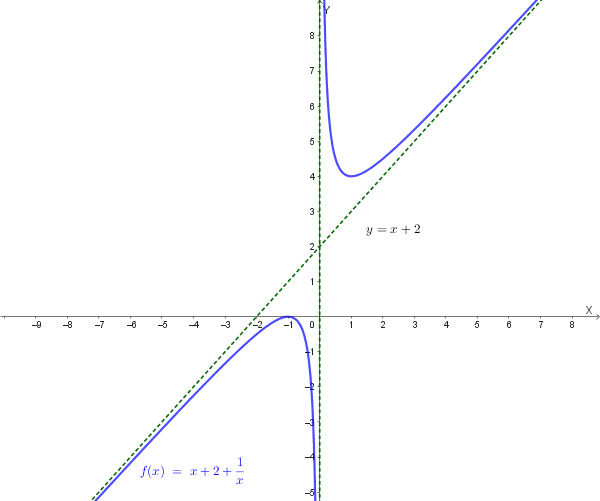
Consideriamo la funzione \(f(x) = x + 2 + \frac{1}{x}\) per \(x \to \pm\infty\).
La funzione è già nella forma \(f(x) = mx + q + g(x)\) con \(m = 1\), \(q = 2\) e \(g(x) = \frac{1}{x}\). Verifichiamo che \(g(x)\) sia infinitesimo: \(\lim_{x \to \pm\infty} \frac{1}{x} = 0\).
Per la dimostrazione, verifichiamo che \(y=x+2\) sia l'asintoto obliquo calcolando \(m\) e \(q\) con la definizione classica:
1. Coefficiente angolare \(m\):
\[ m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \frac{x + 2 + \frac{1}{x}}{x} = \lim_{x \to \pm\infty} \left( 1 + \frac{2}{x} + \frac{1}{x^2} \right) \] \[ m = 1 + 0 + 0 = 1 \]Il coefficiente angolare è \(\mathbf{m = 1}\).
2. Intercetta \(q\):
\[ q = \lim_{x \to \pm\infty} [f(x) - mx] = \lim_{x \to \pm\infty} \left[ \left( x + 2 + \frac{1}{x} \right) - 1x \right] \] \[ q = \lim_{x \to \pm\infty} \left( 2 + \frac{1}{x} \right) = 2 + 0 = 2 \]L'intercetta è \(\mathbf{q = 2}\).
Poiché \(m=1\) e \(q=2\), la retta \(\mathbf{y = x + 2}\) è l'asintoto obliquo per la funzione. La forma \(f(x) = mx + q + g(x)\) è, in pratica, la forma che si ottiene quando si eseguono queste verifiche.
Questo conferma che la scomposizione di una funzione nella forma \(f(x) = mx + q + g(x)\) è un metodo efficace per trovare i suoi asintoti non verticali.