GLI ASINTOTI DI UNA FUNZIONE
![]()
Definizione
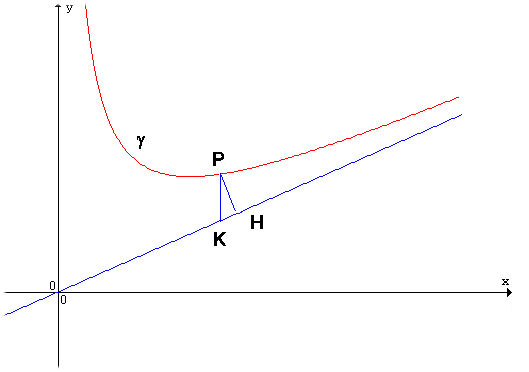
Si dice che la curva g (eventualmente grafico di una funzione di equazione y=f(x)) ammette la retta r come asintoto se la distanza del generico punto P della curva dalla retta r tende a zero quando P si allontana indefinitamente su g.
Riferiamoci ora alle funzioni di equazione y=f(x)
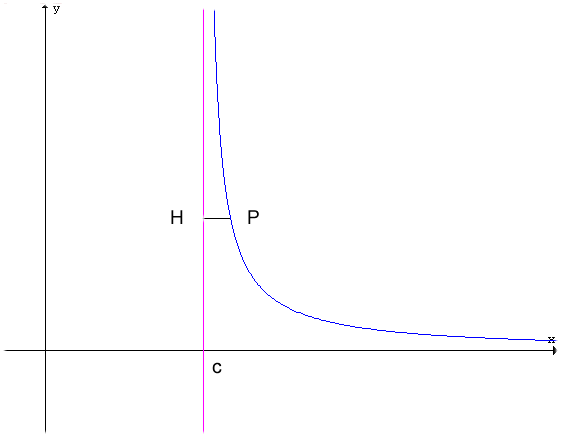
Se ![]() allora la retta di
equazione x=c è asintoto (verticale) della funzione.
allora la retta di
equazione x=c è asintoto (verticale) della funzione.
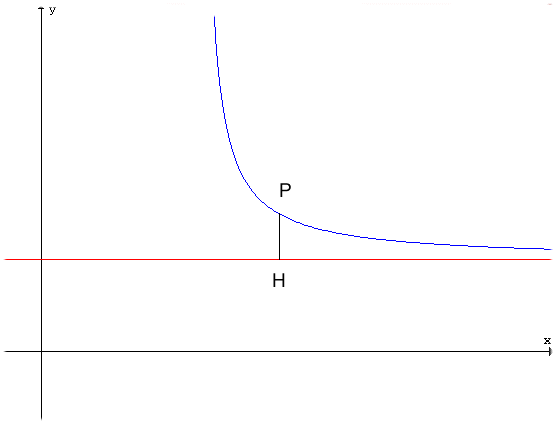
Se ![]() allora la retta di
equazione y = l è asintoto (orizzontale) della funzione.
allora la retta di
equazione y = l è asintoto (orizzontale) della funzione.
N.B. Il grafico di una funzione può intersecare un asintoto orizzontale anche infinite volte mentre può intersecare un asintoto verticale al massimo una volta.
Affinchè la funzione di equazione y=f(x) abbia l'asintoto obliquo di equazione y=mx+q E' NECESSARIO ( MA NON SUFFICIENTE) che
![]()
N.B Il grafico di una funzione può intersecare (anche infinite volte) un asintoto obliquo.
Veniamo ora ad un teorema fondamentale per la ricerca degli asintoti obliqui.
La retta r di equazione y=mx+q è asintoto per la funzione di equazione y=f(x) SE E SOLO SE:
con g(x) infinitesimo per ![]() .
.
Dimostrazione
A)
Hp: vale la (*)
Th: la retta r:y=mx+q è asintoto.
Con riferimento alla prima figura:
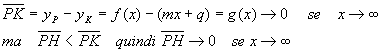
e pertanto r è asintoto per definizione.
B)
Hp: la retta r:y=mx+q è asintoto
Th: vale la (*)
Se r è asintoto ![]() . Ma
. Ma
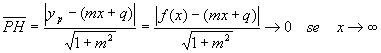
quindi
![]()
E questo vuol dire che
f(x)-(mx+q)=g(x), con g(x) infinitesimo all'infinito; segue facilmente la tesi.
Di uso frequente è il seguente
Teorema 2
La funzione di equazione y=f(x) ammette la retta r di equazione y=mx+q come asintoto SE E SOLO SE valgono le due seguenti proprietà:
Dimostrazione
A)
Hp: r è asintoto
Th: valgono 1) e 2).
Se y=mx+q è asintoto per f(x) dal teorema 1 segue che
f(x)=mx+q+g(x) (*)
con g(x) infinitesimo per ![]() .
.
Risulta:
![]()
ed è quindi verificata la proprietà 1). Si ha poi:
f(x)-mx=q+g(x) che, essendo g(x) infinitesimo, tende a q per ![]() ed è quindi verificata anche la proprietà 2).
ed è quindi verificata anche la proprietà 2).
B)
Hp: valgono 1) e 2)
Th: r è asintoto.
Dalla 2) segue che:
f(x)-mx-q tende a zero se ![]() quindi
quindi
f(x)-mx-q=g(x) con g(x) infinitesimo per ![]() ; si ha pertanto:
; si ha pertanto:
f(x)=mx+q+g(x) e per il teorema 1 si ha la tesi.
Esempi
1) Trovare gli asintoti della funzione di equazione ![]()
2) Trovare gli asintoti della funzione di equazione y=e-x ( x ex + 1 )
La funzione può essere espressa nella forma
![]()
da cui si vede facilmente che non ci sono asintoti verticali.
Per gli asintoti obliqui notiamo che 1/ex è infinitesimo per ![]() , quindi in tal caso si ha
l'asintoto di equazione y=x (per il teorema 1); per
, quindi in tal caso si ha
l'asintoto di equazione y=x (per il teorema 1); per ![]() invece 1/ex tende a +
infinito, pertanto in tal caso la funzione non ammette asintoto obliquo, nè asintoto
orizzontale.
invece 1/ex tende a +
infinito, pertanto in tal caso la funzione non ammette asintoto obliquo, nè asintoto
orizzontale.
3) Trovare gli asintoti della funzione di equazione ![]()
Risulta:
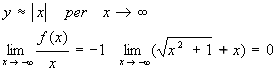
Quindi per ![]() abbiamo l'asintoto di
equazione y=-x
abbiamo l'asintoto di
equazione y=-x
Analogamente si ha:
![]()
Quindi per ![]() abbiamo l'asintoto di
equazione y=x.
abbiamo l'asintoto di
equazione y=x.
IL CASO DELLE FUNZIONI RAZIONALI FRATTE
Una funzione razionale fratta (quoziente di due polinomi interi in x) ammette asintoto obliquo SE E SOLO SE il grado del numeratore supera di 1 il grado del denominatore; l'equazione dell'asintoto è y= Q (x), dove Q (x) è il quoziente della divisione del numeratore per il denominatore.
Poniamo
![]()
Possiamo esprimere la frazione nella forma
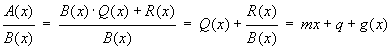
dove Q ed R sono rispettivamente il quoziente ed il resto della divisione di A per B;
in base alle ipotesi Q è di primo grado (1=grado di A - grado di B) ed R è di grado
inferiore a quello di B, quindi g (x) è un infinitesimo per ![]() .
.
La tesi segue quindi dal teorema 1
Esempio
![]()
Dividendo il numeratore per il denominatore si ottiene come quoziente Q (x) =x e come resto R (x) =5x+2.
Quindi si ha l'asintoto di equazione y=x, sia al -infinito che al +infinito.
Osserviamo che la funzione può essere espressa nella forma
![]()