Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.


Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
Trova l'equazione della parabola con vertice nell'origine \(V(0,0)\) e fuoco nel punto \(F(0, 1)\). Successivamente:
Soluzione quesito 1:
La parabola ha vertice in \(V(0,0)\) e fuoco in \(F(0,1)\). L'asse di simmetria è l'asse \(y\), e l'equazione canonica è della forma \(y = ax^2\).
Le coordinate del fuoco sono \(F(0, \frac{1}{4a})\). Eguagliando le coordinate del fuoco, troviamo il valore di \(a\):
\[ \frac{1}{4a} = 1 \Rightarrow a = \frac{1}{4} \]L'equazione della parabola è quindi \(y = \frac{1}{4}x^2\).
Il grafico della parabola \(y = \frac{1}{4}x^2\) ha il vertice nell'origine \(V(0,0)\) e si apre verso l'alto. Puoi tracciarlo usando alcuni punti chiave, come \((2, 1)\) e \((-2, 1)\).
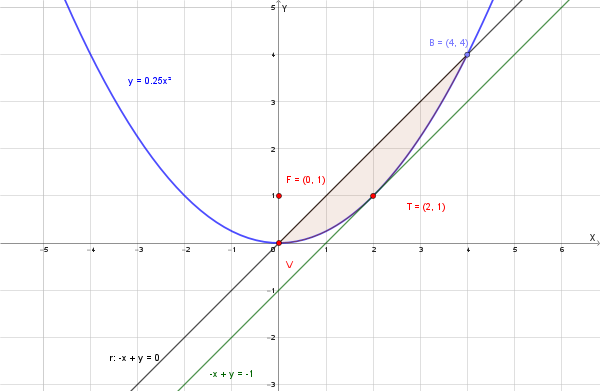
Per trovare l'equazione della tangente \(t\) nel punto \(T\) di ascissa \(x_T = 2\), calcoliamo l'ordinata di \(T\) sulla parabola:
\[ y_T = \frac{1}{4}(2)^2 = 1 \]Il punto di tangenza è \(T(2, 1)\). L'equazione di una retta generica passante per \(T\) è \(y - 1 = m(x - 2)\).
Mettiamo a sistema l'equazione della retta e quella della parabola e imponiamo che il discriminante \(\Delta\) sia uguale a zero per trovare \(m\):
\[ \frac{1}{4}x^2 = m(x - 2) + 1 \Rightarrow \frac{1}{4}x^2 - mx + 2m - 1 = 0 \] \[ \Delta = (-m)^2 - 4\left(\frac{1}{4}\right)(2m - 1) = m^2 - 2m + 1 = (m-1)^2 = 0 \]Da cui otteniamo \(m=1\).
Sostituendo \(m=1\) nell'equazione della retta, troviamo la tangente \(t\):
\[ y - 1 = 1(x - 2) \Rightarrow y = x - 1 \]La base del segmento è una retta parallela a \(t\), quindi con pendenza \(m=1\), che passa per il punto \(A\) di ascissa \(x_A=4\). Troviamo l'ordinata di \(A\): \(y_A = \frac{1}{4}(4)^2 = 4\). Il punto è \(A(4, 4)\).
L'equazione della retta secante passante per \(A\) è \(y - 4 = 1(x - 4) \Rightarrow y = x\). L'altro punto di intersezione con la parabola è l'origine, \(B(0,0)\). La base del segmento parabolico è la corda \(AB\).
Per calcolare l'area del segmento parabolico, applichiamo il **Teorema di Archimede** calcolando l'area del rettangolo circoscritto, che è delimitato dalla retta tangente \(t\) e dalla retta secante \(AB\).
Base del rettangolo (lunghezza della corda AB):
La lunghezza della corda \(AB\) si calcola usando la formula della distanza tra due punti \(A(4,4)\) e \(B(0,0)\):
\[ \text{base} = \sqrt{(4-0)^2 + (4-0)^2} = \sqrt{16 + 16} = \sqrt{32} = 4\sqrt{2} \]Altezza del rettangolo (distanza tra la retta secante e la tangente):
L'altezza è la distanza tra la retta secante \(AB\) (\(y=x \Rightarrow x-y=0\)) e la retta tangente \(t\) (\(y=x-1 \Rightarrow x-y-1=0\)). Poiché le rette sono parallele, possiamo calcolare la distanza tra esse prendendo un punto qualsiasi su una delle due rette (ad esempio il punto di tangenza \(T(2,1)\) sulla retta \(t\)) e calcolandone la distanza dalla retta \(AB\).
\[ \text{altezza} = \frac{|Ax_T + By_T + C|}{\sqrt{A^2 + B^2}} = \frac{|1(2) - 1(1) + 0|}{\sqrt{1^2 + (-1)^2}} = \frac{|1|}{\sqrt{2}} = \frac{1}{\sqrt{2}} \]Area del rettangolo circoscritto:
\[ \text{Area}_{\text{rettangolo}} = \text{base} \times \text{altezza} = 4\sqrt{2} \times \frac{1}{\sqrt{2}} = 4 \]Area del segmento parabolico:
Per il Teorema di Archimede, l'area del segmento parabolico è pari a \(\frac{2}{3}\) dell'area del rettangolo circoscritto:
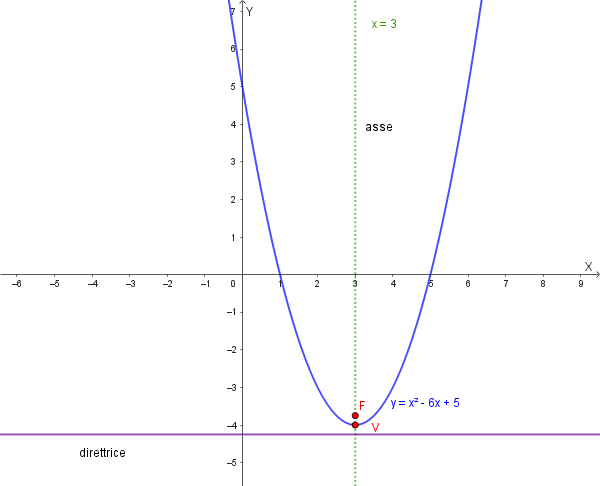
\[ \text{Area}_{\text{segmento}} = \frac{2}{3} \cdot \text{Area}_{\text{rettangolo}} = \frac{2}{3} \cdot 4 = \frac{8}{3} \]Data la parabola di equazione \(y = x^2 - 6x + 5\), trova le coordinate del vertice e del fuoco, le equazioni dell'asse di simmetria e della direttrice, e rappresenta graficamente la parabola.
Soluzione quesito 2:
La parabola ha equazione \(y = x^2 - 6x + 5\), che è della forma \(y = ax^2 + bx + c\), con \(a=1\), \(b=-6\) e \(c=5\).
L'ascissa del vertice si calcola con la formula \(x_V = -\frac{b}{2a}\):
\[ x_V = -\frac{-6}{2(1)} = \frac{6}{2} = 3 \]L'equazione dell'asse di simmetria è \(x = x_V\), quindi l'asse di simmetria è \(x = 3\).
Per trovare l'ordinata del vertice \(y_V\), sostituiamo il valore di \(x_V\) nell'equazione della parabola:
\[ y_V = (3)^2 - 6(3) + 5 = 9 - 18 + 5 = -4 \]Il vertice della parabola è quindi \(V(3, -4)\).
La coordinata \(x\) del fuoco è la stessa del vertice, quindi \(x_F = x_V = 3\). La coordinata \(y\) del fuoco si calcola con la formula \(y_F = y_V + \frac{1}{4a}\):
\[ y_F = -4 + \frac{1}{4(1)} = -4 + \frac{1}{4} = -\frac{16}{4} + \frac{1}{4} = -\frac{15}{4} \]Le coordinate del fuoco sono \(F(3, -\frac{15}{4})\).
L'equazione della direttrice si calcola con la formula \(y = y_V - \frac{1}{4a}\):
\[ y = -4 - \frac{1}{4(1)} = -4 - \frac{1}{4} = -\frac{16}{4} - \frac{1}{4} = -\frac{17}{4} \]L'equazione della direttrice è \(y = -\frac{17}{4}\).
Per tracciare il grafico della parabola, notiamo che si apre verso l'alto (poiché \(a=1 > 0\)), ha il vertice in \(V(3, -4)\) e l'asse di simmetria in \(x=3\). Inoltre, possiamo trovare i punti di intersezione con gli assi cartesiani:
Scrivi l'equazione della circonferenza con centro nel punto \(C(2, -1)\) e raggio \(r = 4\). Successivamente:
Soluzione quesito 3:
L'equazione canonica di una circonferenza con centro \(C(x_C, y_C)\) e raggio \(r\) è \((x - x_C)^2 + (y - y_C)^2 = r^2\).
Sostituendo le coordinate del centro \(C(2, -1)\) e il raggio \(r=4\):
\[ (x - 2)^2 + (y - (-1))^2 = 4^2 \Rightarrow (x - 2)^2 + (y + 1)^2 = 16 \]Espandendo, l'equazione in forma generale è: \(x^2 + y^2 - 4x + 2y - 11 = 0\).
---La circonferenza ha centro in \(C(2, -1)\) e raggio \(r=4\). Per disegnarla, si può tracciare un cerchio con centro nel punto \((2, -1)\) e raggio di 4 unità.
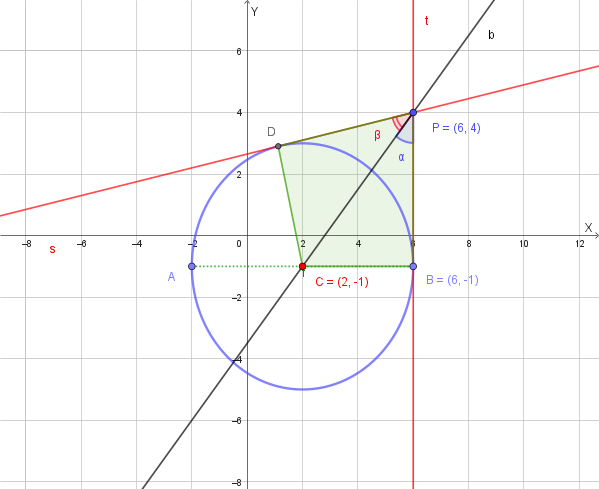
Per trovare le tangenti da un punto esterno \(P(6,4)\), usiamo il metodo del discriminante. L'equazione di una generica retta passante per \(P\) è \(y - 4 = m(x - 6)\), che può essere scritta come \(y = mx - 6m + 4\).
Mettiamo a sistema la retta e la circonferenza:
\[ (x - 2)^2 + ((mx - 6m + 4) + 1)^2 = 16 \] \[ (x - 2)^2 + (mx - 6m + 5)^2 = 16 \]Svolgendo i calcoli e raccogliendo i termini in \(x^2\), \(x\) e il termine noto, si ottiene un'equazione di secondo grado in \(x\). Imponendo il discriminante \(\Delta = 0\) si trova la pendenza \(m\).
Un'alternativa più semplice è utilizzare la distanza dal centro \(C(2, -1)\) alla retta, che deve essere uguale al raggio \(r=4\). La retta è \(mx - y + (4 - 6m) = 0\).
\[ \frac{|m(2) - (-1) + (4 - 6m)|}{\sqrt{m^2 + (-1)^2}} = 4 \] \[ |2m + 1 + 4 - 6m| = 4\sqrt{m^2 + 1} \] \[ |-4m + 5| = 4\sqrt{m^2 + 1} \]Elevando al quadrato entrambi i membri:
\[ (-4m+5)^2 = 16(m^2+1) \Rightarrow 16m^2 - 40m + 25 = 16m^2 + 16 \] \[ -40m = 16 - 25 \Rightarrow -40m = -9 \Rightarrow m = \frac{9}{40} \]Abbiamo trovato una soluzione, \(m = \frac{9}{40}\). Sostituendo questo valore nell'equazione della retta: \(y - 4 = \frac{9}{40}(x - 6) \Rightarrow y = \frac{9}{40}x - \frac{54}{40} + 4 \Rightarrow y = \frac{9}{40}x + \frac{106}{40}\), che si semplifica in \(y = \frac{9}{40}x + \frac{53}{20}\).
La seconda tangente è una retta verticale, poiché il coefficiente angolare non è definito. La retta verticale passante per \(P(6,4)\) è \(x = 6\). La distanza di questa retta dal centro \(C(2,-1)\) è \(|6-2| = 4\), che è esattamente il raggio. Quindi, anche \(x=6\) è una retta tangente.
Le equazioni delle due tangenti sono: \(y = \frac{9}{40}x + \frac{53}{20}\) e \(x = 6\).
---Il quadrilatero \(BCDP\) è un deltoide (aquilone) formato da due triangoli rettangoli congruenti, \(\triangle PCD\) e \(\triangle PCB\). L'area del quadrilatero è il doppio dell'area di uno di questi triangoli. Poiché la retta \(x=6\) è tangente alla circonferenza, il punto di tangenza \(D\) ha coordinate \((6, -1)\). I cateti del triangolo rettangolo \(\triangle PCD\) sono il raggio \(CD\) e il segmento di tangente \(PD\). Le loro lunghezze possono essere calcolate direttamente.
L'area del triangolo \(\triangle PCD\) si calcola come la metà del prodotto dei cateti:
\[ \text{Area}_{\triangle PCD} = \frac{1}{2} \cdot \text{base} \cdot \text{altezza} = \frac{1}{2} \cdot CD \cdot PD = \frac{1}{2} \cdot 4 \cdot 5 = 10 \]L'area totale del quadrilatero \(BCDP\) è il doppio di questa area:
\[ \text{Area}_{BCDP} = 2 \cdot \text{Area}_{\triangle PCD} = 2 \cdot 10 = 20 \] ---Verifica con Geometria Elementare:
I triangoli \(\triangle PBC\) e \(\triangle PDC\) sono entrambi triangoli rettangoli. Entrambi condividono l'ipotenusa \(PC\), e i cateti \(BC\) e \(CD\) sono congruenti in quanto raggi della stessa circonferenza. Per il criterio di congruenza dei triangoli rettangoli (cateto-ipotenusa), i due triangoli sono congruenti.
Poiché i triangoli sono congruenti, anche i loro angoli corrispondenti sono uguali. In particolare, l'angolo \(\angle BPC\) è uguale all'angolo \(\angle DPC\). Questo dimostra che la retta \(PC\) è la bisettrice dell'angolo \(\angle BPD\).
Verifica con Geometria Analitica:
La retta bisettrice di un angolo è il luogo dei punti equidistanti dai due lati dell'angolo. I lati dell'angolo \(\angle BPD\) sono le due rette tangenti che abbiamo trovato: \(r_1: x - 6 = 0\) e \(r_2: y = \frac{9}{40}x + \frac{106}{40}\), che in forma implicita è \(9x - 40y + 106 = 0\).
L'equazione della retta bisettrice è data da:
\[ \frac{|x - 6|}{\sqrt{1^2 + 0^2}} = \frac{|9x - 40y + 106|}{\sqrt{9^2 + (-40)^2}} \] \[ |x - 6| = \frac{|9x - 40y + 106|}{\sqrt{81 + 1600}} = \frac{|9x - 40y + 106|}{41} \]Da questa equazione, si ottengono le due rette bisettrici, risolvendo per i due possibili segni:
Bisettrice 1:
\[ 41(x - 6) = 9x - 40y + 106 \] \[ 41x - 246 = 9x - 40y + 106 \] \[ 32x + 40y - 352 = 0 \]Bisettrice 2:
\[ 41(x - 6) = -(9x - 40y + 106) \] \[ 41x - 246 = -9x + 40y - 106 \] \[ 50x - 40y - 140 = 0 \Rightarrow 5x - 4y - 14 = 0 \]La seconda bisettrice passa per P e C, quindi la bisettrice richiesta è \(5x - 4y - 14 = 0\).
---L'angolo \(\alpha = \angle BPC\) fa parte del triangolo rettangolo \(\triangle PBC\), con l'angolo retto in \(B\). I lati del triangolo sono:
Possiamo calcolare le funzioni trigonometriche direttamente da questi valori:
\[ \sin(\alpha) = \frac{\text{cateto opposto}}{\text{ipotenusa}} = \frac{BC}{PC} = \frac{4}{\sqrt{41}} \] \[ \cos(\alpha) = \frac{\text{cateto adiacente}}{\text{ipotenusa}} = \frac{PB}{PC} = \frac{5}{\sqrt{41}} \] \[ \tan(\alpha) = \frac{\text{cateto opposto}}{\text{cateto adiacente}} = \frac{BC}{PB} = \frac{4}{5} \]Data la circonferenza di equazione \(x^2 + y^2 + 8x - 2y - 8 = 0\), trova le coordinate del centro e il raggio.
Si consideri la corda AB con A=(-7,-3) e B=(-1,-3). Si calcoli l'area del più piccolo dei segmenti circolari delimitato dalla circonferenza e dalla corda AB.
Soluzione quesito 4:
L'equazione data è \(x^2 + y^2 + 8x - 2y - 8 = 0\), che è della forma \(x^2 + y^2 + ax + by + c = 0\), con \(a=8\), \(b=-2\) e \(c=-8\).
Le coordinate del centro si trovano usando le formule \(x_C = -\frac{a}{2}\) e \(y_C = -\frac{b}{2}\):
\[ x_C = -\frac{8}{2} = -4 \] \[ y_C = -\frac{-2}{2} = 1 \]Il centro della circonferenza è \(C(-4, 1)\).
Il raggio si calcola con la formula \(r = \sqrt{\left(-\frac{a}{2}\right)^2 + \left(-\frac{b}{2}\right)^2 - c}\):
\[ r = \sqrt{(-4)^2 + (1)^2 - (-8)} = \sqrt{16 + 1 + 8} = \sqrt{25} = 5 \]Il raggio della circonferenza è \(r=5\).
Ecco una rappresentazione grafica che illustra la circonferenza, il centro, il raggio e la corda AB:
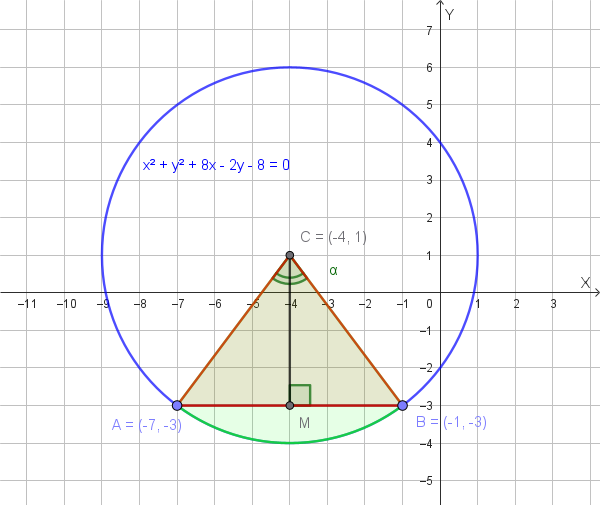
L'area del segmento circolare è data dalla differenza tra l'area del settore circolare \(CAB\) e l'area del triangolo \(ABC\).
Il triangolo \(ABC\) ha vertici \(A(-7,-3)\), \(B(-1,-3)\) e \(C(-4,1)\). Poiché la corda \(AB\) è orizzontale (i punti hanno la stessa ordinata), possiamo calcolare facilmente la sua base e la sua altezza.
L'area del triangolo \(ABC\) è:
\[ \text{Area}_{\triangle ABC} = \frac{1}{2} \cdot \text{base} \cdot \text{altezza} = \frac{1}{2} \cdot 6 \cdot 4 = 12 \]L'area del settore circolare si calcola con la formula \(\text{Area}_{\text{settore}} = \frac{1}{2} r^2 \alpha\), dove \(\alpha\) è l'angolo al centro in radianti. Per trovare l'angolo \(\alpha = \angle ACB\), consideriamo il triangolo rettangolo formato dal centro \(C\), un estremo della corda (ad esempio \(B\)) e il punto medio della corda \(M(-4, -3)\). In questo triangolo rettangolo, i cateti sono \(CM=4\) e \(BM=3\), e l'ipotenusa è il raggio \(r=5\).
Possiamo calcolare il coseno dell'angolo \(\angle BCM\):
\[ \cos(\angle BCM) = \frac{\text{cateto adiacente}}{\text{ipotenusa}} = \frac{CM}{CB} = \frac{4}{5} \]L'angolo al centro \(\alpha\) è il doppio dell'angolo \(\angle BCM\), quindi possiamo usare la formula di duplicazione del coseno \(\cos(\alpha) = 2\cos^2(\angle BCM) - 1\):
\[ \cos(\alpha) = 2\left(\frac{4}{5}\right)^2 - 1 = 2\left(\frac{16}{25}\right) - 1 = \frac{32}{25} - 1 = \frac{32 - 25}{25} = \frac{7}{25} \]Da cui l'angolo \(\alpha = \arccos\left(\frac{7}{25}\right)\). Ora possiamo calcolare l'area del settore:
\[ \text{Area}_{\text{settore}} = \frac{1}{2} r^2 \alpha = \frac{1}{2} (5)^2 \arccos\left(\frac{7}{25}\right) = \frac{25}{2} \arccos\left(\frac{7}{25}\right) \]L'area approssimata del settore è \(12.5 \times 1.287\) radianti \(\approx 16.09\).
L'area del segmento circolare è la differenza tra l'area del settore e l'area del triangolo:
\[ \text{Area}_{\text{segmento}} = \text{Area}_{\text{settore}} - \text{Area}_{\triangle ABC} \] \[ \text{Area}_{\text{segmento}} = \frac{25}{2} \arccos\left(\frac{7}{25}\right) - 12 \]Il valore approssimato dell'area è \(16.09 - 12 = 4.09\).
Trova l'equazione di un'ellisse con centro nell'origine, fuochi sull'asse \(x\), un semiasse maggiore di lunghezza \(a=5\) e un semiasse minore di lunghezza \(b=3\).
Soluzione quesito 5:
L'equazione canonica di un'ellisse con centro nell'origine e fuochi sull'asse \(x\) è: \[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \] Ci vengono fornite le lunghezze dei semiassi: \(a=5\) (semiasse maggiore sull'asse \(x\)) e \(b=3\) (semiasse minore sull'asse \(y\)). Sostituiamo questi valori nell'equazione: \[ \frac{x^2}{5^2} + \frac{y^2}{3^2} = 1 \] \[ \frac{x^2}{25} + \frac{y^2}{9} = 1 \] Questa è l'equazione dell'ellisse richiesta.
---Per trovare le coordinate dei fuochi \(F_1\) e \(F_2\), dobbiamo calcolare la semidistanza focale \(c\) utilizzando la relazione \(c^2 = a^2 - b^2\): \[ c^2 = 5^2 - 3^2 = 25 - 9 = 16 \] \[ c = \sqrt{16} = 4 \] Poiché i fuochi sono sull'asse \(x\), le loro coordinate sono \(F_1(-4, 0)\) e \(F_2(4, 0)\). I vertici dell'ellisse sono i punti di intersezione con gli assi cartesiani. Dato che \(a=5\) e \(b=3\), i vertici sono:
L'eccentricità \(e\) si calcola con la formula \(e = \frac{c}{a}\): \[ e = \frac{4}{5} = 0.8 \] Poiché \(0 < e < 1\), si conferma che la conica è un'ellisse.
---Per prima cosa, troviamo l'ordinata del punto \(T\) con ascissa \(x_T = 3\) e ordinata positiva. Sostituiamo \(x=3\) nell'equazione dell'ellisse: \[ \frac{3^2}{25} + \frac{y^2}{9} = 1 \] \[ \frac{9}{25} + \frac{y^2}{9} = 1 \Rightarrow \frac{y^2}{9} = 1 - \frac{9}{25} = \frac{16}{25} \] \[ y^2 = \frac{16}{25} \cdot 9 = \frac{144}{25} \Rightarrow y = \pm \frac{12}{5} \] Poiché l'ordinata è positiva, il punto di tangenza è \(T\left(3, \frac{12}{5}\right)\). Per trovare l'equazione della tangente in un punto dell'ellisse, usiamo la formula di sdoppiamento: \[ \frac{x \cdot x_0}{a^2} + \frac{y \cdot y_0}{b^2} = 1 \] Sostituiamo le coordinate di \(T(x_0, y_0) = \left(3, \frac{12}{5}\right)\), \(a^2=25\) e \(b^2=9\): \[ \frac{x \cdot 3}{25} + \frac{y \cdot \frac{12}{5}}{9} = 1 \] \[ \frac{3x}{25} + \frac{12y}{45} = 1 \] Semplifichiamo il secondo termine e moltiplichiamo tutto per il minimo comune multiplo (225) per eliminare i denominatori: \[ \frac{3x}{25} + \frac{4y}{15} = 1 \] \[ 9 \cdot 3x + 15 \cdot 4y = 225 \] \[ 27x + 60y = 225 \] Dividiamo tutti i termini per 3 per semplificare: \[ 9x + 20y = 75 \] L'equazione della tangente è \(9x + 20y - 75 = 0\).
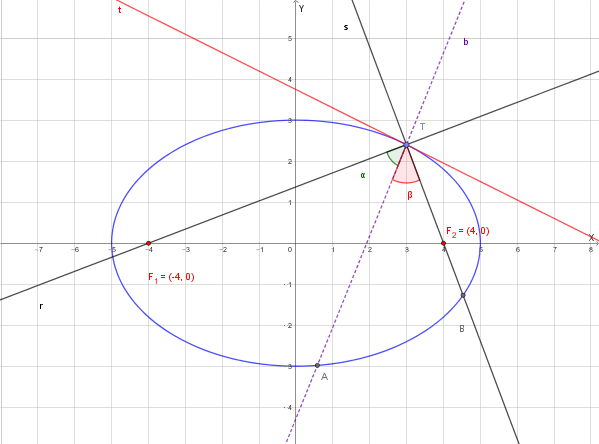
---La **proprietà ottica dell'ellisse** afferma che la retta tangente in un punto qualsiasi dell'ellisse è la **bisettrice dell'angolo esterno** formato dalle rette che congiungono quel punto con i due fuochi. In altre parole, la tangente biseca l'angolo supplementare all'angolo \(\angle F_1TF_2\).
Questa proprietà ha un'importante conseguenza fisica: un raggio luminoso che parte da uno dei fuochi si riflette sulla superficie dell'ellisse e passa per l'altro fuoco.
Per dimostrare questa proprietà per il nostro caso, dobbiamo verificare che gli angoli formati dalla tangente con i segmenti \(TF_1\) e \(TF_2\) sono uguali. L'approccio più semplice è usare la formula della bisettrice.
Abbiamo le equazioni delle rette che congiungono il punto \(T\left(3, \frac{12}{5}\right)\) con i fuochi \(F_1(-4, 0)\) e \(F_2(4, 0)\):
Per trovare le equazioni delle bisettrici, usiamo la formula: \[ \frac{|12x - 35y + 48|}{\sqrt{12^2 + (-35)^2}} = \frac{|12x + 5y - 48|}{\sqrt{12^2 + 5^2}} \] Semplifichiamo i denominatori: \[ \sqrt{144 + 1225} = \sqrt{1369} = 37 \] \[ \sqrt{144 + 25} = \sqrt{169} = 13 \] L'equazione diventa: \[ \frac{|12x - 35y + 48|}{37} = \frac{|12x + 5y - 48|}{13} \] Questa equazione si sdoppia in due casi, uno con il segno positivo (+) e uno con il segno negativo (-):
Caso 1: Segno Positivo (+) \[ 13(12x - 35y + 48) = 37(12x + 5y - 48) \] \[ 156x - 455y + 624 = 444x + 185y - 1776 \] Spostiamo tutti i termini a sinistra e semplifichiamo: \[ (156x - 444x) + (-455y - 185y) + (624 + 1776) = 0 \] \[ -288x - 640y + 2400 = 0 \] Dividiamo per \(-32\) per semplificare l'equazione: \[ 9x + 20y - 75 = 0 \] Questa bisettrice coincide con la tangente t: quindi la proprietà è dimostrata.
Data l'equazione dell'ellisse \(\frac{(x-1)^2}{16} + \frac{y^2}{25} = 1\), rispondi alle seguenti domande:
Soluzione quesito 6:
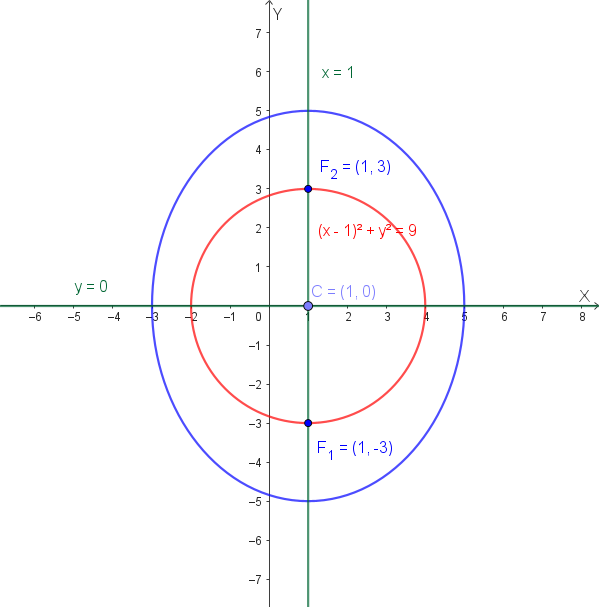
L'equazione è \(\frac{(x-1)^2}{16} + \frac{y^2}{25} = 1\). Questa è un'ellisse traslata con centro non più nell'origine, ma in \(C(1, 0)\). Poiché il denominatore di \(y^2\) è maggiore del denominatore di \((x-1)^2\) (\(25 > 16\)), l'asse maggiore è verticale e parallelo all'asse \(y\).
I semiassi hanno lunghezza \(a=4\) (orizzontale) e \(b=5\) (verticale).
---Per rappresentare graficamente l'ellisse, abbiamo bisogno di trovare il suo centro, i vertici e i fuochi.
Per i fuochi, calcoliamo la semidistanza focale \(c\) con la relazione \(c^2 = b^2 - a^2\): \[ c^2 = 25 - 16 = 9 \] \[ c = \sqrt{9} = 3 \] I fuochi si trovano sull'asse maggiore, quindi le loro coordinate sono \(F_1(1, 0-3) = (1, -3)\) e \(F_2(1, 0+3) = (1, 3)\).
Vogliamo trasformare l'ellisse \(\frac{(x-1)^2}{16} + \frac{y^2}{25} = 1\) in una circonferenza con lo stesso centro \(C(1, 0)\) e raggio \(R=3\). L'equazione di questa circonferenza è \((X-1)^2 + Y^2 = 9\), che può essere scritta come \(\frac{(X-1)^2}{9} + \frac{Y^2}{9} = 1\).
Per trovare le equazioni della trasformazione, confrontiamo i termini delle due equazioni. \[ \frac{(x-1)^2}{16} = \frac{(X-1)^2}{9} \quad \Rightarrow \quad \frac{x-1}{4} = \frac{X-1}{3} \] \[ 3(x-1) = 4(X-1) \quad \Rightarrow \quad 3x - 3 = 4X - 4 \quad \Rightarrow \quad 4X = 3x + 1 \quad \Rightarrow \quad X = \frac{3}{4}x + \frac{1}{4} \] In questo caso, il centro dell'ellisse trasformata non è più \(C(1,0)\) ma è stato spostato. Rifacciamo i calcoli con maggiore attenzione, confrontando i termini in modo da mantenere il centro. \[ \frac{(x-1)^2}{16} = \frac{(X-1)^2}{9} \quad \Rightarrow \quad \frac{x-1}{4} = \frac{X-1}{3} \] \[ \frac{y^2}{25} = \frac{Y^2}{9} \quad \Rightarrow \quad \frac{y}{5} = \frac{Y}{3} \] Dalle due uguaglianze, possiamo ricavare le equazioni della trasformazione, che sono affinità con i seguenti coefficienti: \[ \frac{x-1}{4} = \frac{X-1}{3} \quad \Rightarrow \quad X-1 = \frac{3}{4}(x-1) \quad \Rightarrow \quad X = \frac{3}{4}x - \frac{3}{4} + 1 \quad \Rightarrow \quad X = \frac{3}{4}x + \frac{1}{4} \] \[ \frac{y}{5} = \frac{Y}{3} \quad \Rightarrow \quad Y = \frac{3}{5}y \] La trasformazione richiesta è quindi l'affinità di equazioni: \[ \begin{cases} X = \frac{3}{4}x + \frac{1}{4} \\ Y = \frac{3}{5}y \end{cases} \]
---Il rapporto tra l'area di una figura geometrica e l'area della sua immagine dopo una trasformazione affine è costante. Questo rapporto è uguale al valore assoluto del determinante della matrice associata alla trasformazione. In una trasformazione del tipo \(\begin{cases} X = k_x x + c_x \\ Y = k_y y + c_y \end{cases}\), il determinante è semplicemente il prodotto dei fattori di scala, ovvero \(|k_x \cdot k_y|\). Nel nostro caso, i fattori di scala sono \(k_x = \frac{3}{4}\) e \(k_y = \frac{3}{5}\).
Il rapporto tra le aree è: \[ k = \left| \frac{3}{4} \cdot \frac{3}{5} \right| = \frac{9}{20} \] L'area della figura trasformata (la circonferenza) è \(A_{circ} = \pi R^2\), dove \(R=3\). \[ A_{circ} = \pi \cdot 3^2 = 9\pi \] Poiché il rapporto delle aree è \(\frac{A_{circ}}{A_{ellisse}} = k\), possiamo trovare l'area dell'ellisse: \[ A_{ellisse} = \frac{A_{circ}}{k} = \frac{9\pi}{\frac{9}{20}} = 9\pi \cdot \frac{20}{9} = 20\pi \] L'area dell'ellisse è \(20\pi\) unità quadrate. Questo risultato coincide con la formula standard dell'area di un'ellisse, \(A = \pi a b\), dove \(a=4\) e \(b=5\), quindi \(A = \pi \cdot 4 \cdot 5 = 20\pi\).
Trova l'equazione dell'iperbole con centro nell'origine, fuochi sull'asse \(x\), e avente vertici in \((\pm 4, 0)\) e fuochi in \((\pm 5, 0)\).
Soluzione quesito 7:
L'equazione canonica di un'iperbole con centro nell'origine e fuochi sull'asse \(x\) è della forma: \[ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \] I vertici sono in \((\pm a, 0)\), quindi \(a=4\). I fuochi sono in \((\pm c, 0)\), quindi \(c=5\).
Per trovare il valore di \(b\), usiamo la relazione \(c^2 = a^2 + b^2\):
\[ 5^2 = 4^2 + b^2 \] \[ 25 = 16 + b^2 \] \[ b^2 = 25 - 16 = 9 \Rightarrow b = 3 \]Sostituiamo i valori di \(a^2\) e \(b^2\) nell'equazione dell'iperbole:
\[ \frac{x^2}{4^2} - \frac{y^2}{3^2} = 1 \] \[ \frac{x^2}{16} - \frac{y^2}{9} = 1 \] ---L'eccentricità \(e\) di un'iperbole con fuochi sull'asse \(x\) si calcola con la formula \(e = \frac{c}{a}\).
Abbiamo già i valori di \(c=5\) e \(a=4\), quindi: \[ e = \frac{c}{a} = \frac{5}{4} = 1.25 \] Poiché \(e > 1\), si conferma che la conica è un'iperbole.
---Per disegnare l'iperbole, abbiamo bisogno di alcuni elementi chiave:
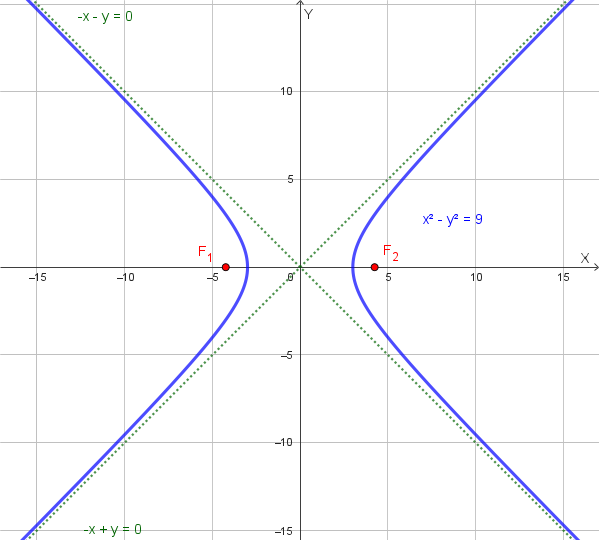
Vogliamo trasformare l'iperbole \(\frac{x^2}{16} - \frac{y^2}{9} = 1\) nell'iperbole equilatera \(X^2 - Y^2 = 9\). L'equazione di quest'ultima può essere riscritta come \(\frac{X^2}{9} - \frac{Y^2}{9} = 1\).
Per trovare le equazioni della trasformazione, confrontiamo i termini delle due equazioni. Sia \((x, y)\) un punto sull'iperbole di partenza e \((X, Y)\) il suo corrispondente sulla nuova iperbole. \[ \frac{x^2}{16} = \frac{X^2}{9} \quad \Rightarrow \quad \frac{x}{4} = \frac{X}{3} \quad \Rightarrow \quad X = \frac{3}{4}x \] \[ \frac{y^2}{9} = \frac{Y^2}{9} \quad \Rightarrow \quad \frac{y}{3} = \frac{Y}{3} \quad \Rightarrow \quad Y = y \] La trasformazione geometrica richiesta è quindi una **dilatazione orizzontale** e ha equazioni: \[ \begin{cases} X = \frac{3}{4}x \\ Y = y \end{cases} \] L'iperbole equilatera \(X^2 - Y^2 = 9\) ha vertici in \((\pm 3, 0)\) e asintoti con equazioni \(Y = \pm X\). Il suo grafico è quello dell'iperbole di partenza che viene "contratta" orizzontalmente.

L'equazione dell'iperbole di partenza è \(\frac{x^2}{16} - \frac{y^2}{9} = 1\). Possiamo usare l'identità trigonometrica \(\frac{1}{\cos^2(t)} - \tan^2(t) = 1\), che è equivalente a \(\sec^2(t) - \tan^2(t) = 1\). Confrontando le due equazioni, possiamo impostare: \[ \frac{x^2}{16} = \frac{1}{\cos^2(t)} \quad \Rightarrow \quad \frac{x}{4} = \frac{1}{\cos(t)} \quad \Rightarrow \quad x = \frac{4}{\cos(t)} \] \[ \frac{y^2}{9} = \tan^2(t) \quad \Rightarrow \quad \frac{y}{3} = \tan(t) \quad \Rightarrow \quad y = 3\tan(t) \] Le equazioni parametriche dell'iperbole sono: \[ \begin{cases} x = \frac{4}{\cos(t)} \\ y = 3\tan(t) \end{cases} \] dove \(t\) è un parametro. Queste equazioni rappresentano i due rami dell'iperbole al variare di \(t\). Poiché \(\frac{1}{\cos(t)}\) è definita per tutti i valori di \(t\) tranne quando \(\cos(t) = 0\), le equazioni non sono definite per \(t = \frac{\pi}{2} + k\pi\), dove \(k\) è un numero intero. Questa parametrizzazione è un modo efficace per descrivere i punti sull'iperbole senza usare un'equazione cartesiana.
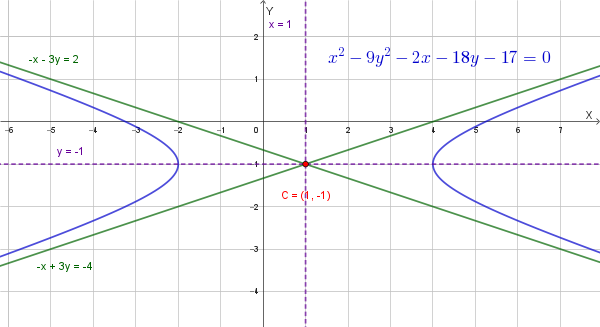
Data l'iperbole di equazione \(x^2 - 9y^2 - 2x - 18y - 17 = 0\), trova le equazioni dei suoi asintoti e rappresentala graficamente.
Soluzione quesito 8:
L'equazione data non è nella sua forma canonica, ma è un'iperbole traslata. Per trovare i suoi asintoti e rappresentarla, dobbiamo prima riscriverla in forma canonica utilizzando il **metodo del completamento del quadrato**.
Raggruppiamo i termini con \(x\) e quelli con \(y\): \[ (x^2 - 2x) - (9y^2 + 18y) - 17 = 0 \] Raccogliamo il coefficiente di \(y^2\): \[ (x^2 - 2x) - 9(y^2 + 2y) - 17 = 0 \] Aggiungiamo e sottraiamo i termini necessari per formare i quadrati di binomio. Per il termine \(x\), il "mezzo" del coefficiente è \(\frac{-2}{2} = -1\), e il suo quadrato è \(1\). Per il termine \(y\), il "mezzo" del coefficiente è \(\frac{2}{2} = 1\), e il suo quadrato è \(1\). \[ (x^2 - 2x + 1) - 1 - 9(y^2 + 2y + 1) + 9 - 17 = 0 \] Semplifichiamo e riscriviamo l'equazione in forma canonica: \[ (x - 1)^2 - 9(y + 1)^2 - 9 = 0 \] \[ (x - 1)^2 - 9(y + 1)^2 = 9 \] Dividiamo per 9 per ottenere la forma standard: \[ \frac{(x - 1)^2}{9} - \frac{9(y + 1)^2}{9} = \frac{9}{9} \] \[ \frac{(x - 1)^2}{9} - (y + 1)^2 = 1 \] Questa è l'equazione dell'iperbole in forma canonica. Da essa ricaviamo il centro \(C(1, -1)\), \(a^2=9 \Rightarrow a=3\) e \(b^2=1 \Rightarrow b=1\).
---Gli asintoti passano per il centro \(C(1, -1)\) e hanno pendenza \(m = \pm \frac{b}{a}\). \[ m = \pm \frac{1}{3} \] Usiamo la formula della retta passante per un punto \((x_0, y_0)\) con una data pendenza \(m\): \(y - y_0 = m(x - x_0)\).
Asintoto 1 (pendenza positiva): \[ y - (-1) = \frac{1}{3}(x - 1) \] \[ y + 1 = \frac{1}{3}x - \frac{1}{3} \] \[ y = \frac{1}{3}x - \frac{4}{3} \]
Asintoto 2 (pendenza negativa): \[ y - (-1) = -\frac{1}{3}(x - 1) \] \[ y + 1 = -\frac{1}{3}x + \frac{1}{3} \] \[ y = -\frac{1}{3}x - \frac{2}{3} \] Le equazioni degli asintoti sono \(y = \frac{1}{3}x - \frac{4}{3}\) e \(y = -\frac{1}{3}x - \frac{2}{3}\).
---Per disegnare l'iperbole, iniziamo tracciando il suo centro \(C(1, -1)\). I vertici si trovano sull'asse orizzontale (poiché \(x^2\) è il termine positivo) a una distanza \(a=3\) dal centro.
Poi disegniamo gli asintoti che passano per il centro. L'iperbole passa per i vertici e si avvicina sempre di più agli asintoti man mano che ci si allontana dal centro.
Data la funzione \(y = \frac{3x+1}{x-2}\):
Soluzione quesito 9:
La funzione data è una funzione omografica, che rappresenta un'iperbole equilatera con asintoti paralleli agli assi cartesiani. Per studiarla, troviamo gli asintoti che ne definiscono il centro e la posizione.
L'asintoto verticale si trova annullando il denominatore della frazione: \[ x-2=0 \quad \Rightarrow \quad x=2 \] L'equazione dell'asintoto verticale è \(x=2\).
L'asintoto orizzontale è: \[ y = \frac{3}{1} = 3 \]
Il centro dell'iperbole è l'intersezione degli asintoti, ovvero \(C(2,3)\). Per rappresentare graficamente l'iperbole, possiamo tracciare gli asintoti e poi calcolare alcuni punti per avere un'idea della forma delle due "branche". Ad esempio, per \(x=0\), \(y = \frac{1}{-2} = -0.5\); per \(x=1\), \(y = \frac{4}{-1} = -4\).
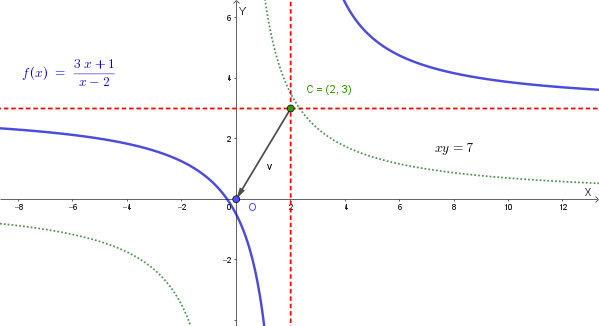
Per ricondurre l'iperbole traslata \(y = \frac{3x+1}{x-2}\) alla forma \(XY=k\), dobbiamo applicare una **traslazione** che sposti il centro dell'iperbole dall'intersezione degli asintoti \(C(2,3)\) all'origine \((0,0)\) del nuovo sistema di riferimento \((X, Y)\). Le equazioni della traslazione sono: \[ \begin{cases} X = x - x_C \\ Y = y - y_C \end{cases} \] Sostituiamo le coordinate del centro \(C(2,3)\): \[ \begin{cases} X = x - 2 \\ Y = y - 3 \end{cases} \] Ora, esprimiamo \(x\) e \(y\) in funzione di \(X\) e \(Y\): \[ \begin{cases} x = X + 2 \\ y = Y + 3 \end{cases} \] Sostituiamo queste espressioni nell'equazione di partenza: \[ Y + 3 = \frac{3(X + 2) + 1}{(X + 2) - 2} \] \[ Y + 3 = \frac{3X + 6 + 1}{X} \] \[ Y + 3 = \frac{3X + 7}{X} \] \[ Y = \frac{3X + 7}{X} - 3 \] \[ Y = \frac{3X + 7 - 3X}{X} \] \[ Y = \frac{7}{X} \] Moltiplicando per \(X\), otteniamo l'equazione finale: \[ XY = 7 \] Le equazioni della trasformazione geometrica sono \(\begin{cases} X = x - 2 \\ Y = y - 3 \end{cases}\) e riconducono l'iperbole data alla forma canonica \(XY=7\).
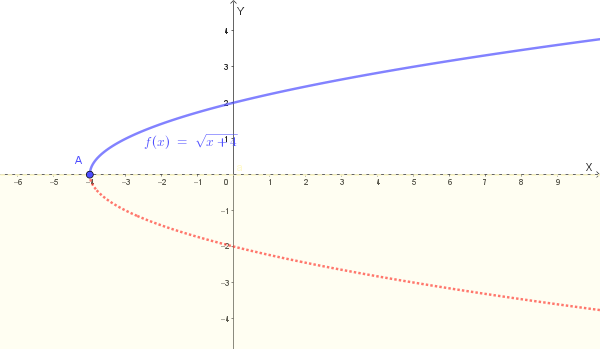
Considera la funzione \(y = \sqrt{x+4}\). Descrivi il grafico di questa funzione e dimostra come sia riconducibile a una parabola.
Soluzione quesito 10:
La funzione \(y = \sqrt{x+4}\) è definita solo per i valori di \(x\) per cui l'argomento della radice è non negativo, cioè \(x+4 \ge 0 \Rightarrow x \ge -4\). Inoltre, il valore della funzione \(y\) sarà sempre non negativo, cioè \(y \ge 0\).
Per riconoscerla come una conica, possiamo elevare al quadrato entrambi i lati dell'equazione:
\[ y^2 = (\sqrt{x+4})^2 \] \[ y^2 = x+4 \]Questa è l'equazione di una parabola del tipo \(x = ay^2 + by + c\), con \(a=1\), \(b=0\) e \(c=4\). Poiché il termine in \(y\) è al quadrato, l'asse di simmetria è orizzontale, parallelo all'asse \(x\).
Il vertice si trova nel punto in cui il termine tra parentesi si annulla, cioè per \(x = -4\). Sostituendo in \(y^2 = x+4\), otteniamo \(y=0\). Il vertice è \(V(-4, 0)\).
Il grafico di \(y = \sqrt{x+4}\) è solo il ramo superiore della parabola \(y^2 = x+4\), poiché abbiamo imposto la condizione \(y \ge 0\).