Ripasso sulle Coniche

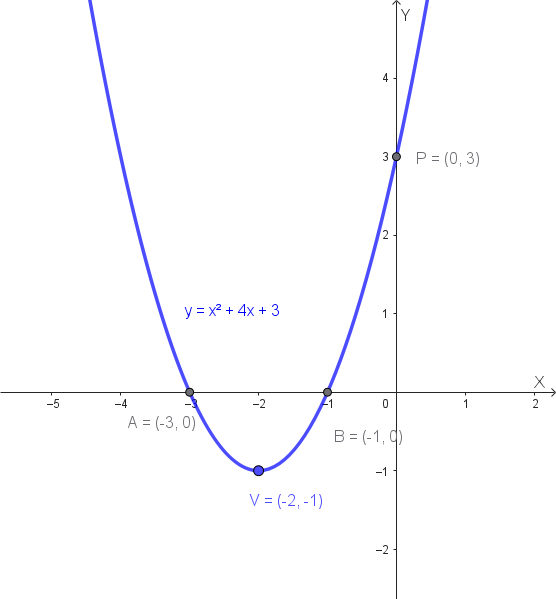
1) Trovare l'equazione di una parabola dato il vertice e un punto, e rappresentarla graficamente

Dato il vertice \(V(-2, -1)\) e il punto \(P(0, 3)\), l'equazione della parabola è del tipo \(y = a(x - x_V)^2 + y_V\). Sostituiamo le coordinate del vertice:

\[ y = a(x - (-2))^2 - 1 \] \[ y = a(x + 2)^2 - 1 \]

Ora usiamo le coordinate del punto \(P(0, 3)\) per trovare \(a\):

\[ 3 = a(0 + 2)^2 - 1 \] \[ 3 = a(4) - 1 \] \[ 4 = 4a \] \[ a = 1 \]

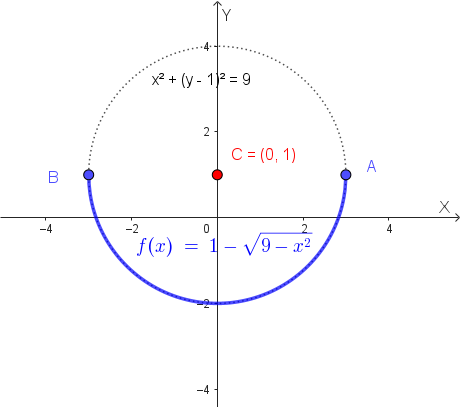
L'equazione finale è: \[ y = (x + 2)^2 - 1 \implies y = x^2 + 4x + 3 \]

Per rappresentare graficamente la parabola, troviamo le sue intersezioni con gli assi cartesiani. Oltre al vertice \(V(-2, -1)\), abbiamo già il punto \(P(0, 3)\), che è l'intersezione con l'asse y.

Troviamo le intersezioni con l'asse x (dove \(y = 0\)):

\[ x^2 + 4x + 3 = 0 \]

Risolviamo l'equazione di secondo grado:

\[ x = \frac{-4 \pm \sqrt{4^2 - 4(1)(3)}}{2} = \frac{-4 \pm \sqrt{16 - 12}}{2} = \frac{-4 \pm \sqrt{4}}{2} = \frac{-4 \pm 2}{2} \]

Otteniamo due soluzioni:

\[ x_A = \frac{-4 - 2}{2} = -3 \implies A(-3, 0) \]

\[ x_B = \frac{-4 + 2}{2} = -1 \implies B(-1, 0) \]

Il grafico della parabola è quindi il seguente:

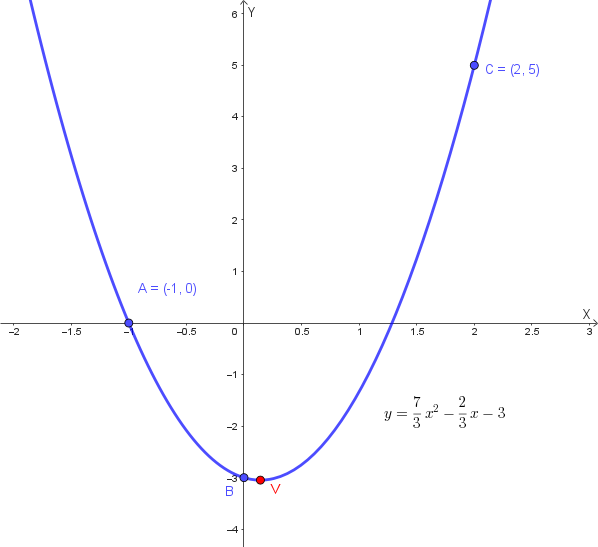
2) Trovare l'equazione di una parabola passante per tre punti e rappresentarla graficamente

Dati i punti \(A(-1, 0)\), \(B(0, -3)\), \(C(2, 5)\), sostituiamo le loro coordinate nell'equazione generale \(y = ax^2 + bx + c\) per creare un sistema di tre equazioni in tre incognite (a, b, c):

• Punto A: \(0 = a(-1)^2 + b(-1) + c \implies a - b + c = 0\)
• Punto B: \(-3 = a(0)^2 + b(0) + c \implies c = -3\)
• Punto C: \(5 = a(2)^2 + b(2) + c \implies 4a + 2b + c = 5\)

Sostituendo \(c=-3\) nelle altre due equazioni, si ottiene un sistema più semplice:

\[ a - b - 3 = 0 \implies a = b + 3 \] \[ 4a + 2b - 3 = 5 \implies 4a + 2b = 8 \]

Sostituiamo la prima equazione nella seconda:

\[ 4(b + 3) + 2b = 8 \] \[ 4b + 12 + 2b = 8 \] \[ 6b = -4 \implies b = -\frac{4}{6} = -\frac{2}{3} \]

Ora troviamo \(a\):

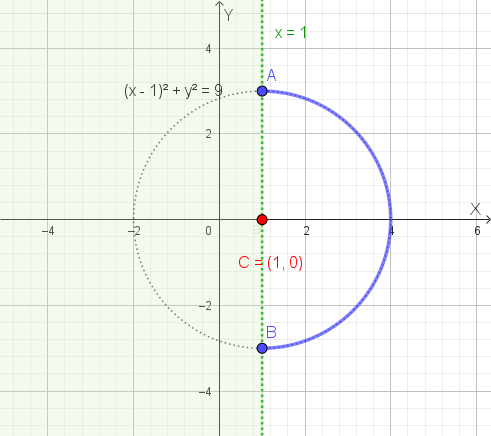
\[ a = b + 3 = -\frac{2}{3} + 3 = \frac{-2 + 9}{3} = \frac{7}{3} \]

L'equazione finale è: \[ y = \frac{7}{3}x^2 - \frac{2}{3}x - 3 \]

Per rappresentare graficamente la parabola, troviamo le sue intersezioni con gli assi cartesiani e il vertice. I punti dati sono già due intersezioni con l'asse x e l'asse y.

Intersezioni con gli assi:

• Intersezione con l'asse y: Il punto B(0, -3) è già la nostra intersezione con l'asse y (dove x=0).
• Intersezioni con l'asse x: Il punto A(-1, 0) è una delle intersezioni. Per trovare l'altra, risolviamo l'equazione \( \frac{7}{3}x^2 - \frac{2}{3}x - 3 = 0 \).

\[ 7x^2 - 2x - 9 = 0 \] \[ x = \frac{2 \pm \sqrt{(-2)^2 - 4(7)(-9)}}{2(7)} = \frac{2 \pm \sqrt{4 + 252}}{14} = \frac{2 \pm \sqrt{256}}{14} = \frac{2 \pm 16}{14} \]

Otteniamo due soluzioni:

\[ x_1 = \frac{2 - 16}{14} = -1 \implies (-1, 0) \] \[ x_2 = \frac{2 + 16}{14} = \frac{18}{14} = \frac{9}{7} \implies \left(\frac{9}{7}, 0\right) \]

Vertice della parabola:

Il vertice si trova a metà strada tra le intersezioni con l'asse x:

\[ x_V = \frac{-1 + \frac{9}{7}}{2} = \frac{\frac{-7 + 9}{7}}{2} = \frac{\frac{2}{7}}{2} = \frac{1}{7} \]

Oppure, usiamo la formula \( x_V = -\frac{b}{2a} \):

\[ x_V = -\frac{-\frac{2}{3}}{2(\frac{7}{3})} = \frac{\frac{2}{3}}{\frac{14}{3}} = \frac{2}{14} = \frac{1}{7} \]

Ora troviamo l'ordinata del vertice sostituendo \(x_V\) nell'equazione della parabola:

\[ y_V = \frac{7}{3}\left(\frac{1}{7}\right)^2 - \frac{2}{3}\left(\frac{1}{7}\right) - 3 = \frac{7}{3}\left(\frac{1}{49}\right) - \frac{2}{21} - 3 = \frac{1}{21} - \frac{2}{21} - 3 = -\frac{1}{21} - 3 = -\frac{64}{21} \]

Il vertice è \(V\left(\frac{1}{7}, -\frac{64}{21}\right)\).

Il grafico della parabola è il seguente:

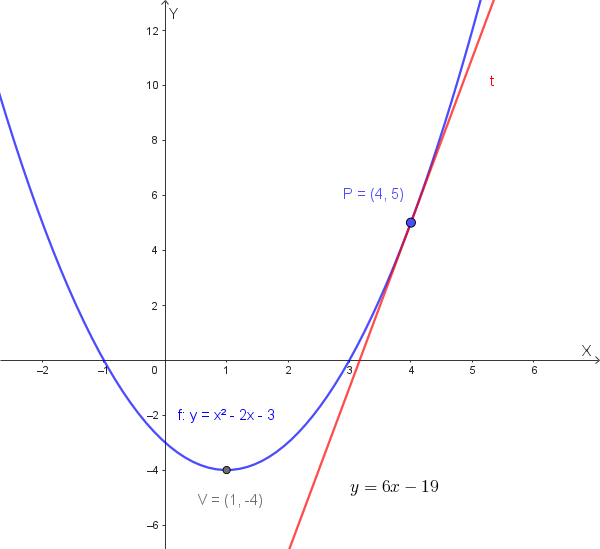
3) Tangente a una parabola in un punto

Consideriamo la parabola di equazione \(y = x^2 - 2x - 3\) e il punto \(P(4, 5)\). Per verificare che il punto appartenga alla parabola, sostituiamo le sue coordinate nell'equazione:

\[ 5 = (4)^2 - 2(4) - 3 \implies 5 = 16 - 8 - 3 \implies 5 = 5 \]

Poiché il punto appartiene alla parabola, possiamo trovare l'equazione della retta tangente. Vediamo due metodi.

Metodo a) Discriminante uguale a zero (\(\Delta=0\))

Consideriamo il fascio di rette passanti per il punto \(P(4, 5)\):

\[ y - 5 = m(x - 4) \implies y = mx - 4m + 5 \]

Sostituiamo questa espressione di \(y\) nell'equazione della parabola:

\[ mx - 4m + 5 = x^2 - 2x - 3 \]

Portiamo tutti i termini a destra per ottenere un'equazione di secondo grado in \(x\):

\[ x^2 - 2x - mx - 3 + 4m - 5 = 0 \]

\[ x^2 - (2 + m)x + (4m - 8) = 0 \]

Affinché la retta sia tangente, l'equazione deve avere una sola soluzione, il che significa che il suo discriminante (\(\Delta\)) deve essere uguale a zero.

Ricordiamo la formula del discriminante: \(\Delta = b^2 - 4ac\). In questo caso, \(a=1\), \(b=-(2+m)\), e \(c=4m-8\).

\[ \Delta = (-(2+m))^2 - 4(1)(4m - 8) = 0 \]

\[ (2+m)^2 - 4(4m - 8) = 0 \]

\[ 4 + 4m + m^2 - 16m + 32 = 0 \]

\[ m^2 - 12m + 36 = 0 \]

Questa è un'equazione di secondo grado in \(m\). Possiamo risolverla con la formula o riconoscere che si tratta di un quadrato perfetto, \((m - 6)^2 = 0\).

La soluzione è \(m = 6\). Questo è il coefficiente angolare della retta tangente. Sostituiamo \(m=6\) nell'equazione del fascio di rette:

\[ y - 5 = 6(x - 4) \]

\[ y - 5 = 6x - 24 \]

\[ y = 6x - 19 \]

Metodo b) Formula di sdoppiamento (metodo più rapido)

Per una parabola \(y = ax^2 + bx + c\), l'equazione della retta tangente in un punto \(P(x_0, y_0)\) è data dalla formula di sdoppiamento:

\[ \frac{y + y_0}{2} = ax_0x + b\frac{x + x_0}{2} + c \]

Nel nostro caso, \(y_0=5\), \(x_0=4\), \(a=1\), \(b=-2\), \(c=-3\).

Sostituiamo questi valori nella formula:

\[ \frac{y + 5}{2} = 1(4)x + (-2)\frac{x + 4}{2} - 3 \]

Semplifichiamo l'equazione:

\[ \frac{y + 5}{2} = 4x - (x + 4) - 3 \]

\[ \frac{y + 5}{2} = 3x - 7 \]

Moltiplichiamo per 2 per eliminare il denominatore:

\[ y + 5 = 2(3x - 7) \]

\[ y + 5 = 6x - 14 \]

Risolviamo per \(y\) per ottenere l'equazione della retta in forma esplicita:

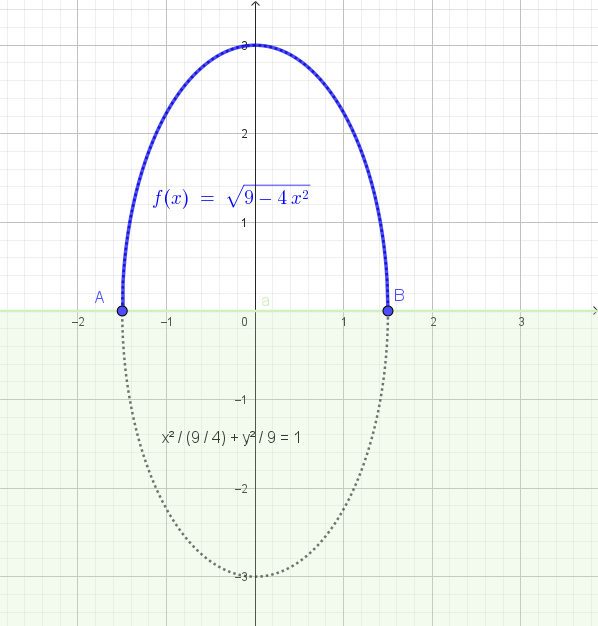
\[ y = 6x - 19 \]

Come puoi vedere, entrambi i metodi portano allo stesso risultato.

---

Rappresentiamo graficamente la parabola e la sua tangente. Per la parabola, troviamo le intersezioni con gli assi e il vertice.

Vertice:

Troviamo il vertice della parabola \(y = x^2 - 2x - 3\) usando la formula \(x_V = -\frac{b}{2a}\) e \(y_V = x_V^2 - 2x_V - 3\):

\[ x_V = -\frac{-2}{2(1)} = 1 \] \[ y_V = (1)^2 - 2(1) - 3 = 1 - 2 - 3 = -4 \]

Il vertice è \(V(1, -4)\).

Intersezioni con gli assi:

• Con l'asse x (\(y=0\)): \[ x^2 - 2x - 3 = 0 \] \[ (x - 3)(x + 1) = 0 \] Le intersezioni sono \(A(-1, 0)\) e \(B(3, 0)\).
• Con l'asse y (\(x=0\)): \[ y = (0)^2 - 2(0) - 3 = -3 \] L'intersezione è \(C(0, -3)\).

Il grafico è il seguente:

Calcolare l'area di un segmento parabolico con il Teorema di Archimede

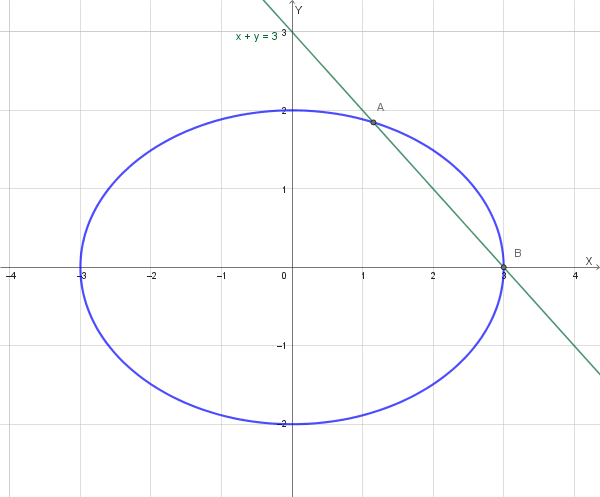
Calcolare l'area del segmento di parabola individuato dalla retta \(y = -x + 6\) e dalla parabola \(y = -x^2 + 5x\).

Risoluzione

Per applicare il **Teorema di Archimede**, che afferma che l'area di un segmento parabolico è pari a \(\frac{2}{3}\) dell'area del rettangolo circoscritto, dobbiamo trovare la base e l'altezza di tale rettangolo.

1. Trovare i punti di intersezione (A e B)

Mettiamo a sistema le due equazioni per trovare i punti in cui la retta interseca la parabola. Questi punti definiscono la corda, che sarà la base del nostro rettangolo.

\[ -x^2 + 5x = -x + 6 \] \[ x^2 - 6x + 6 = 0 \]

Risolviamo l'equazione di secondo grado:

\[ x = \frac{6 \pm \sqrt{36 - 24}}{2} = \frac{6 \pm \sqrt{12}}{2} = \frac{6 \pm 2\sqrt{3}}{2} = 3 \pm \sqrt{3} \]

Le ascisse dei punti di intersezione sono \(x_A = 3 - \sqrt{3}\) e \(x_B = 3 + \sqrt{3}\). Troviamo le ordinate corrispondenti sostituendo i valori nell'equazione della retta:

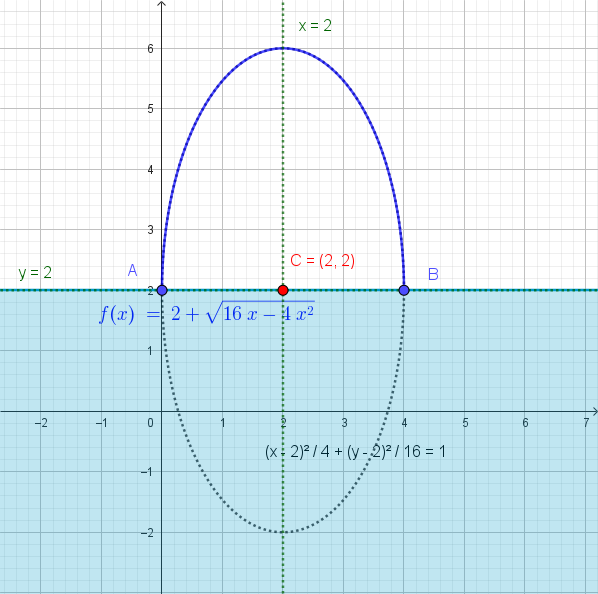
• Per \(x_A = 3 - \sqrt{3}\): \(y_A = -(3 - \sqrt{3}) + 6 = 3 + \sqrt{3} \implies A(3 - \sqrt{3}, 3 + \sqrt{3})\)
• Per \(x_B = 3 + \sqrt{3}\): \(y_B = -(3 + \sqrt{3}) + 6 = 3 - \sqrt{3} \implies B(3 + \sqrt{3}, 3 - \sqrt{3})\)

2. Calcolare la lunghezza della corda (Base del rettangolo)

Usiamo la formula della distanza tra due punti per calcolare la lunghezza della corda AB:

\[ \text{Base} = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2} = \sqrt{((3+\sqrt{3}) - (3-\sqrt{3}))^2 + ((3-\sqrt{3}) - (3+\sqrt{3}))^2} \] \[ \text{Base} = \sqrt{(2\sqrt{3})^2 + (-2\sqrt{3})^2} = \sqrt{12 + 12} = \sqrt{24} = 2\sqrt{6} \]

3. Trovare l'altezza del segmento

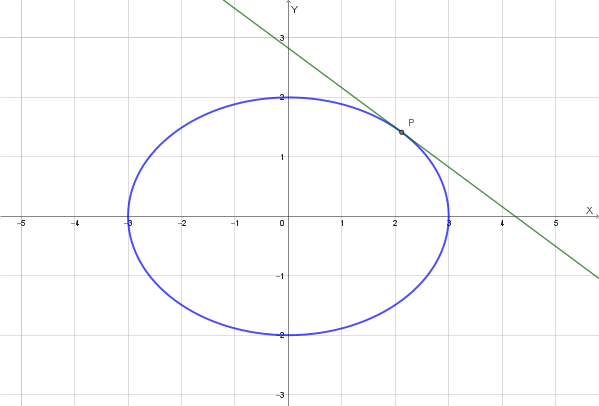
L'altezza del segmento è la distanza tra la retta secante e la retta tangente alla parabola, che è parallela alla secante. Poiché la retta secante ha pendenza \(m = -1\), anche la tangente avrà pendenza \(m = -1\).

Per trovare l'equazione della retta tangente, consideriamo il fascio di rette parallele alla secante, ovvero \(y = -x + q\). Mettiamo a sistema questa equazione con quella della parabola e imponiamo la condizione di tangenza, che si ha quando l'equazione risolvente ha un'unica soluzione, ovvero il suo discriminante (\(\Delta\)) è uguale a zero.

\[ -x^2 + 5x = -x + q \] \[ x^2 - 6x + q = 0 \]

Poniamo il discriminante uguale a zero:

\[ \Delta = b^2 - 4ac = 0 \] \[ (-6)^2 - 4(1)(q) = 0 \] \[ 36 - 4q = 0 \implies 4q = 36 \implies q = 9 \]

La retta tangente ha equazione \(y = -x + 9\).

Ora calcoliamo l'altezza del segmento, che è la distanza tra le due rette parallele, \(y = -x + 6\) e \(y = -x + 9\). Per farlo, calcoliamo la distanza di un punto qualsiasi della prima retta (ad es. il punto B) dalla seconda retta. L'equazione della retta tangente in forma implicita è \(x + y - 9 = 0\).

Usiamo la formula della distanza punto-retta:

\[ \text{Altezza} = \frac{|Ax_B + By_B + C|}{\sqrt{A^2 + B^2}} = \frac{|1(3 + \sqrt{3}) + 1(3 - \sqrt{3}) - 9|}{\sqrt{1^2 + 1^2}} = \frac{|6 - 9|}{\sqrt{2}} = \frac{3}{\sqrt{2}} = \frac{3\sqrt{2}}{2} \]

4. Applicare il Teorema di Archimede

Rappresentiamo graficamente la parabola, la retta secante e il segmento parabolico.

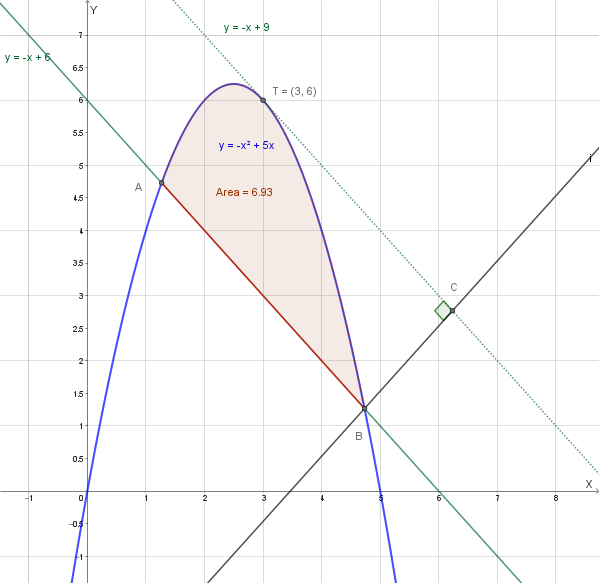
Ora che abbiamo la base e l'altezza, possiamo calcolare l'area del segmento parabolico:

\[ \text{Area} = \frac{2}{3} \cdot \text{Base} \cdot \text{Altezza} = \frac{2}{3} \cdot (2\sqrt{6}) \cdot \left(\frac{3\sqrt{2}}{2}\right) \] \[ \text{Area} = \frac{2 \cdot 2\sqrt{6} \cdot 3\sqrt{2}}{3 \cdot 2} = \frac{12\sqrt{12}}{6} = 2\sqrt{12} = 2 \cdot 2\sqrt{3} = 4\sqrt{3} \]

1) Circonferenza di dato centro e raggio

Dato il centro \(C(1, -2)\) e il raggio \(r=3\), l'equazione della circonferenza si ottiene direttamente dalla formula canonica:

\[ (x - 1)^2 + (y - (-2))^2 = 3^2 \] \[ (x - 1)^2 + (y + 2)^2 = 9 \] \[ x^2 - 2x + 1 + y^2 + 4y + 4 = 9 \] \[ x^2 + y^2 - 2x + 4y - 4 = 0 \]

2) Circonferenza di dato centro e passante per un punto

Dato il centro \(C(2, 3)\) e un punto \(P(5, 7)\) per cui passa la circonferenza, per prima cosa calcoliamo il raggio, che è la distanza tra il centro e il punto:

\[ r = d(C, P) = \sqrt{(5 - 2)^2 + (7 - 3)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]

Ora usiamo la formula canonica con il centro e il raggio trovato:

\[ (x - 2)^2 + (y - 3)^2 = 5^2 \] \[ x^2 - 4x + 4 + y^2 - 6y + 9 = 25 \] \[ x^2 + y^2 - 4x - 6y - 12 = 0 \]

3) Circonferenza di dato diametro

Dati i punti \(A(-3, 1)\) e \(B(5, 5)\) come estremi di un diametro, il centro \(C\) della circonferenza è il punto medio di AB:

\[ C\left(\frac{-3 + 5}{2}, \frac{1 + 5}{2}\right) = C\left(\frac{2}{2}, \frac{6}{2}\right) = C(1, 3) \]

Il raggio \(r\) è la metà della lunghezza del diametro, ovvero la distanza tra il centro C e uno dei due punti (ad esempio A):

\[ r = d(C, A) = \sqrt{(1 - (-3))^2 + (3 - 1)^2} = \sqrt{4^2 + 2^2} = \sqrt{16 + 4} = \sqrt{20} \]

L'equazione della circonferenza è:

\[ (x - 1)^2 + (y - 3)^2 = (\sqrt{20})^2 \] \[ x^2 - 2x + 1 + y^2 - 6y + 9 = 20 \] \[ x^2 + y^2 - 2x - 6y - 10 = 0 \]

4) Circonferenza per tre punti non allineati

Dati tre punti \(A(1, 1)\), \(B(2, 0)\) e \(C(3, 3)\), sostituiamo le loro coordinate nell'equazione generale \(x^2 + y^2 + ax + by + c = 0\) per creare un sistema di tre equazioni in tre incognite (a, b, c):

• Punto A: \(1^2 + 1^2 + a(1) + b(1) + c = 0 \implies a + b + c = -2\)
• Punto B: \(2^2 + 0^2 + a(2) + b(0) + c = 0 \implies 2a + c = -4\)
• Punto C: \(3^2 + 3^2 + a(3) + b(3) + c = 0 \implies 3a + 3b + c = -18\)

Risolvendo il sistema, otteniamo \(a = -5, b = -3, c = 6\). L'equazione finale è:

\[ x^2 + y^2 - 5x - 3y + 6 = 0 \]

5) Tangente a una circonferenza in un punto

Consideriamo la circonferenza \(x^2 + y^2 - 6x - 2y + 5 = 0\) e il punto \(P(2, 3)\) su di essa.

Metodo a) Discriminante uguale a zero

Il fascio di rette passanti per \(P(2, 3)\) ha equazione \(y - 3 = m(x - 2)\), ovvero \(y = mx - 2m + 3\).

Sostituiamo \(y\) nell'equazione della circonferenza e poniamo \(\Delta = 0\):

\[ x^2 + (mx - 2m + 3)^2 - 6x - 2(mx - 2m + 3) + 5 = 0 \]

Dopo aver sviluppato e raggruppato i termini, si ottiene un'equazione di secondo grado in \(x\). Imponendo \(\Delta=0\), si troverà il valore di \(m\).

Metodo b) Perpendicolarità

Per prima cosa, troviamo il centro \(C\) della circonferenza: \(C(-\frac{-6}{2}, -\frac{-2}{2}) = C(3, 1)\).

Il raggio CP è perpendicolare alla tangente nel punto P. Calcoliamo il coefficiente angolare della retta passante per C e P:

\[ m_{CP} = \frac{3 - 1}{2 - 3} = \frac{2}{-1} = -2 \]

Il coefficiente angolare della tangente, che è perpendicolare al raggio, è l'antireciproco: \[ m_{tangente} = -\frac{1}{m_{CP}} = -\frac{1}{-2} = \frac{1}{2} \]

L'equazione della retta tangente è quella che passa per \(P(2, 3)\) con coefficiente angolare \(m = \frac{1}{2}\):

\[ y - 3 = \frac{1}{2}(x - 2) \] \[ 2(y - 3) = x - 2 \] \[ 2y - 6 = x - 2 \] \[ x - 2y + 4 = 0 \]

6) L'asse radicale di due circonferenze

L'**asse radicale** di due circonferenze è la retta del **fascio di circonferenze** generato dalle due curve. L'equazione di un fascio di circonferenze è data da \(\gamma_1 + k\gamma_2 = 0\), e l'asse radicale si ottiene ponendo il parametro \(k = -1\). L'asse radicale è la retta perpendicolare alla retta che unisce i centri delle due circonferenze.

Circonferenze secanti

Quando le due circonferenze si intersecano in due punti distinti, l'asse radicale è la retta che congiunge tali punti di intersezione.

Consideriamo le due circonferenze:

• \(\gamma_1\): \(x^2 + y^2 - 4x - 2y = 0\)
• \(\gamma_2\): \(x^2 + y^2 + 2x + 4y - 6 = 0\)

Sottraiamo membro a membro le due equazioni per ottenere l'asse radicale:

\[ (x^2 + y^2 - 4x - 2y) - (x^2 + y^2 + 2x + 4y - 6) = 0 \] \[ -4x - 2y - 2x - 4y + 6 = 0 \] \[ -6x - 6y + 6 = 0 \implies x + y - 1 = 0 \]

Circonferenze tangenti

Se le circonferenze sono tangenti in un punto, l'asse radicale coincide con la loro tangente comune in quel punto.

Consideriamo le due circonferenze:

• \(\gamma_1\): \(x^2 + y^2 - 2x - 2y + 1 = 0\)
• \(\gamma_2\): \(x^2 + y^2 + 2x + 2y + 1 = 0\)

Sottraendo le due equazioni, si ottiene:

\[ (x^2 + y^2 - 2x - 2y + 1) - (x^2 + y^2 + 2x + 2y + 1) = 0 \] \[ -2x - 2y - 2x - 2y = 0 \implies -4x - 4y = 0 \implies x + y = 0 \]

Circonferenze esterne

Quando le circonferenze non hanno punti di contatto, l'asse radicale non le interseca, ma mantiene la sua proprietà di essere perpendicolare alla retta dei centri.

Consideriamo le due circonferenze:

• \(\gamma_1\): \(x^2 + y^2 - 4 = 0\)
• \(\gamma_2\): \(x^2 + y^2 - 6x - 8y + 24 = 0\)

Sottraendo le equazioni:

\[ (x^2 + y^2 - 4) - (x^2 + y^2 - 6x - 8y + 24) = 0 \] \[ 6x + 8y - 28 = 0 \implies 3x + 4y - 14 = 0 \]

L'asse radicale **non esiste** se le due circonferenze sono **concentriche**.

1) Trovare vertici e fuochi data l'equazione

Data l'ellisse con equazione \( \frac{x^2}{25} + \frac{y^2}{9} = 1 \). Qui \(a^2 = 25 \implies a = 5\) e \(b^2 = 9 \implies b = 3\).

Poiché \(a > b\), i fuochi si trovano sull'asse \(x\).

• Vertici: \(A_1(-5, 0)\), \(A_2(5, 0)\), \(B_1(0, -3)\), \(B_2(0, 3)\).
• Fuochi: Calcoliamo \(c = \sqrt{a^2 - b^2} = \sqrt{25 - 9} = \sqrt{16} = 4\). I fuochi sono \(F_1(-4, 0)\), \(F_2(4, 0)\).

2) Scrivere l'equazione di un'ellisse dati i semiassi

Dati i semiassi \(a=4\) e \(b=2\), l'equazione dell'ellisse con centro nell'origine è:

\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \] \[ \frac{x^2}{4^2} + \frac{y^2}{2^2} = 1 \] \[ \frac{x^2}{16} + \frac{y^2}{4} = 1 \]

Grafico dell'ellisse

3) Scrivere l'equazione di un'ellisse dato un semiasse e un fuoco

Dato il semiasse \(a=5\) e il fuoco \(F_1(-3, 0)\). Il fuoco si trova sull'asse \(x\), quindi \(a\) è il semiasse maggiore. La coordinata del fuoco è \(c=3\).

Possiamo calcolare \(b^2\) dalla relazione \(c^2 = a^2 - b^2 \implies b^2 = a^2 - c^2\).

\[ b^2 = 5^2 - 3^2 = 25 - 9 = 16 \]

L'equazione è:

\[ \frac{x^2}{25} + \frac{y^2}{16} = 1 \]

Grafico dell'ellisse

4) Scrivere l'equazione di un'ellisse dati i vertici e un punto

Dati i vertici sull'asse \(x\) \(A_1(-6, 0)\) e \(A_2(6, 0)\), sappiamo che \(a=6\). L'equazione è del tipo \( \frac{x^2}{36} + \frac{y^2}{b^2} = 1 \).

Se l'ellisse passa per il punto \(P(3, \frac{\sqrt{27}}{2})\), sostituiamo le coordinate del punto nell'equazione per trovare \(b^2\):

\[ \frac{3^2}{36} + \frac{(\frac{\sqrt{27}}{2})^2}{b^2} = 1 \] \[ \frac{9}{36} + \frac{\frac{27}{4}}{b^2} = 1 \] \[ \frac{1}{4} + \frac{27}{4b^2} = 1 \]

\[ \frac{27}{4b^2} = 1 - \frac{1}{4} = \frac{3}{4} \] \[ 27 \cdot 4 = 3 \cdot 4b^2 \] \[ 108 = 12b^2 \] \[ b^2 = 9 \]

L'equazione finale è: \[ \frac{x^2}{36} + \frac{y^2}{9} = 1 \]

Grafico dell'ellisse

5) Trovare le eventuali intersezioni fra un'ellisse e una retta

Consideriamo l'ellisse \( \frac{x^2}{9} + \frac{y^2}{4} = 1 \). Trova le intersezioni con le seguenti rette:

• Retta Secante: \(x + y = 3 \implies y = 3 - x\). Sostituiamo nell'equazione dell'ellisse:
  \[ \frac{x^2}{9} + \frac{(3 - x)^2}{4} = 1 \] \[ 4x^2 + 9(9 - 6x + x^2) = 36 \] \[ 4x^2 + 81 - 54x + 9x^2 = 36 \] \[ 13x^2 - 54x + 45 = 0 \]

  Calcolando il \(\Delta = (-54)^2 - 4(13)(45) = 2916 - 2340 = 576 > 0\). Essendo il \(\Delta > 0\), ci sono due soluzioni reali e distinte, quindi la retta è secante e interseca l'ellisse in due punti.

  Grafico dell'ellisse

  
• Retta Tangente: \(2x + 3y - 6\sqrt{2} = 0 \implies y = -\frac{2}{3}x + 2\sqrt{2}\). Sostituiamo:
  \[ \frac{x^2}{9} + \frac{(-\frac{2}{3}x + 2\sqrt{2})^2}{4} = 1 \]

  Sviluppando e risolvendo, si otterrà un'equazione di secondo grado con \(\Delta = 0\), indicando che la retta è tangente e ha un solo punto di intersezione.

  Grafico dell'ellisse

  
• Retta Esterna: \(x + y = 5 \implies y = 5 - x\). Sostituiamo:
  \[ \frac{x^2}{9} + \frac{(5 - x)^2}{4} = 1 \]

  Sviluppando e risolvendo, si otterrà un'equazione con \(\Delta < 0\), indicando che la retta è esterna e non interseca l'ellisse.

  Grafico dell'ellisse

  

6) Tangente a un'ellisse in un punto

Consideriamo l'ellisse \( \frac{x^2}{16} + \frac{y^2}{4} = 1 \) e il punto \( P(2\sqrt{3}, 1) \).

Metodo del discriminante (\(\Delta=0\))

Il fascio di rette passanti per \(P(2\sqrt{3}, 1)\) è \(y - 1 = m(x - 2\sqrt{3})\).

Sostituiamo \(y\) nell'equazione dell'ellisse e poniamo il discriminante uguale a zero. Si otterrà il valore del coefficiente angolare \(m\) della retta tangente.

Metodo di sdoppiamento

Questo metodo è molto più rapido per trovare la tangente se si conosce un punto sull'ellisse. Sostituiamo \(x^2\) con \(x_0x\) e \(y^2\) con \(y_0y\), dove \((x_0, y_0)\) sono le coordinate del punto di tangenza.

L'equazione di tangenza è: \[ \frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1 \]

Nel nostro caso, \(x_0 = 2\sqrt{3}\) e \(y_0 = 1\), con \(a^2=16\) e \(b^2=4\):

\[ \frac{(2\sqrt{3})x}{16} + \frac{(1)y}{4} = 1 \] \[ \frac{\sqrt{3}x}{8} + \frac{y}{4} = 1 \]

Moltiplichiamo per 8 per eliminare i denominatori:

\[ \sqrt{3}x + 2y = 8 \implies \sqrt{3}x + 2y - 8 = 0 \]

Questa è l'equazione della retta tangente.

Grafico:

Esempio: Iperbole con fuochi sull'asse x

Consideriamo l'equazione \( \frac{x^2}{25} - \frac{y^2}{9} = 1 \). In questo caso, il termine \(x^2\) è positivo, quindi i fuochi sono sull'asse \(x\).

• I semiassi sono \(a^2 = 25 \implies a = 5\) e \(b^2 = 9 \implies b = 3\).
• La semidistanza focale è \(c = \sqrt{a^2 + b^2} = \sqrt{25 + 9} = \sqrt{34}\).
• I fuochi sono \(F_1(-\sqrt{34}, 0)\) e \(F_2(\sqrt{34}, 0)\).
• Gli asintoti hanno equazione \(y = \pm \frac{b}{a}x\), quindi \(y = \pm \frac{3}{5}x\).

Esempio: Iperbole con fuochi sull'asse y

Consideriamo l'equazione \( \frac{y^2}{16} - \frac{x^2}{4} = 1 \). In questo caso, il termine \(y^2\) è positivo, quindi i fuochi sono sull'asse \(y\).

• I semiassi sono \(b^2 = 16 \implies b = 4\) e \(a^2 = 4 \implies a = 2\).
• La semidistanza focale è \(c = \sqrt{a^2 + b^2} = \sqrt{4 + 16} = \sqrt{20} = 2\sqrt{5}\).
• I fuochi sono \(F_1(0, -2\sqrt{5})\) e \(F_2(0, 2\sqrt{5})\).
• Gli asintoti hanno equazione \(y = \pm \frac{b}{a}x\), quindi \(y = \pm \frac{4}{2}x \implies y = \pm 2x\).

1) \(y = \sqrt{4 - x^2}\)

Elevando al quadrato entrambi i membri, otteniamo \(y^2 = 4 - x^2\), che può essere riscritta come \(x^2 + y^2 = 4\). Questa è l'equazione di una **circonferenza** con centro nell'origine e raggio \(r=2\). Tuttavia, la condizione \(y \ge 0\) imposta dalla radice quadrata fa sì che il grafico sia solo la **semicirconferenza superiore**.

2) \(y = 1 - \sqrt{9 - x^2}\)

Isolando la radice e elevando al quadrato, si ottiene \(x^2 + (y-1)^2 = 9\). Si tratta di una **circonferenza** con centro in \(C(0, 1)\) e raggio \(r=3\). Poiché la radice ha un segno negativo, la condizione \(y \le 1\) limita il grafico alla **semicirconferenza inferiore**.

3) \(x = 1 + \sqrt{9 - y^2}\)

Isolando la radice e elevando al quadrato, si ottiene \((x-1)^2 + y^2 = 9\). Anche questa è una **circonferenza** con centro in \(C(1, 0)\) e raggio \(r=3\). La condizione \(x \ge 1\) limita il grafico alla **semicirconferenza destra**.

4) \(y = \sqrt{9 - 4x^2}\)

Elevando al quadrato e riordinando, si ottiene \(4x^2 + y^2 = 9\). Dividendo per 9, si ha \(\frac{x^2}{9/4} + \frac{y^2}{9} = 1\). Questa è un'**ellisse** con semiassi \(a=3/2\) e \(b=3\). La condizione \(y \ge 0\) limita il grafico alla **semielisse superiore**.

5) \(y = 2 + \sqrt{16x - 4x^2}\)

Isolando la radice e completando il quadrato, si ottiene \(\frac{(x-2)^2}{4} + \frac{(y-2)^2}{16} = 1\). Si tratta di un'**ellisse traslata** con centro in \(C(2, 2)\) e semiassi \(a=2\) e \(b=4\). La condizione \(y \ge 2\) limita il grafico alla **semielisse superiore**.

6) \(y = -\sqrt{x^2 + 1}\)

Elevando al quadrato, si ottiene \(y^2 = x^2 + 1\), ovvero \(y^2 - x^2 = 1\). Questa è l'equazione di un'**iperbole** con fuochi sull'asse \(y\). La condizione \(y \le 0\) imposta dal segno negativo della radice limita il grafico al **ramo inferiore** dell'iperbole.

7) \(y = 2 + \sqrt{4x^2 + 4}\)

Isolando la radice e elevando al quadrato, si ottiene \((y-2)^2 - 4x^2 = 4\). Dividendo per 4, si ha \(\frac{(y-2)^2}{4} - x^2 = 1\). Questa è un'**iperbole traslata** con centro in \(C(0, 2)\) e fuochi sull'asse parallelo a \(y\). La condizione \(y \ge 2\) limita il grafico al **ramo superiore**.

8) \(y = \frac{|x| - 2}{x}\)

Per la presenza del valore assoluto, dobbiamo distinguere due casi. Per \(x > 0\), si ha \(y = \frac{x-2}{x} = 1 - \frac{2}{x}\). Per \(x < 0\), si ha \(y = \frac{-x-2}{x} = 1 + \frac{2}{x}\). Entrambe le equazioni rappresentano rami di un'**iperbole equilatera** con asintoti \(x=0\) e \(y=1\).