Questionario sugli Integrali Indefiniti

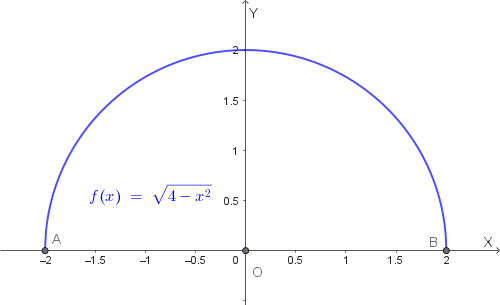
La funzione è definita quando il radicando è non negativo:

\[4-x^2 \ge 0 \quad \Rightarrow \quad -2 \le x \le 2\]

Il dominio è quindi: \[D_f = [-2,2].\]

Poiché \[f(-x)=\sqrt{4-(-x)^2}=\sqrt{4-x^2}=f(x),\] la funzione è pari e il grafico è simmetrico rispetto all’asse \(y\).

Le intersezioni con gli assi sono:

• Asse \(x\): \(x=\pm 2\);
• Asse \(y\): \(f(0)=2\).

Elevando al quadrato l’equazione \(y=\sqrt{4-x^2}\) si ottiene: \[x^2+y^2=4,\] che rappresenta una circonferenza di centro l’origine e raggio 2. Poiché \(y \ge 0\), il grafico della funzione è la semicirconferenza superiore.

Calcoliamo l’integrale: \[\int \sqrt{4-x^2}\,dx\]

Utilizziamo una sostituzione trigonometrica ponendo: \[x = 2\sin t \quad \Rightarrow \quad dx = 2\cos t\,dt.\]

Si ha: \[\sqrt{4-x^2} = \sqrt{4-4\sin^2 t}=2\cos t.\]

L’integrale diventa quindi: \[\int 2\cos t \cdot 2\cos t\,dt=4\int \cos^2 t\,dt.\]

Ricordando la formula di duplicazione \(\cos^2 t = \frac{1+\cos 2t}{2}\), otteniamo: \[4\int \frac{1+\cos 2t}{2}\,dt=2\int (1+\cos 2t)\,dt = 2\left(t+\frac{\sin 2t}{2}\right)+C=2t+\sin 2t+C.\]

Tornando alla variabile \(x\):

• \(t=\arcsin\!\left(\frac{x}{2}\right)\)
• \(\sin 2t = 2\sin t\cos t= \frac{x}{2}\sqrt{4-x^2}\)

La primitiva deve passare per il punto \(\left(\sqrt{3},\,\frac{\sqrt{3}}{2}+\frac{2\pi}{3}\right)\).

Calcoliamo \(F(\sqrt{3})\): \[\sqrt{4-(\sqrt{3})^2}=1,\quad\arcsin\!\left(\frac{\sqrt{3}}{2}\right)=\frac{\pi}{3}\]

Risulta: \[F(\sqrt{3})=\frac{\sqrt{3}}{2}+2\cdot\frac{\pi}{3}+C=\frac{\sqrt{3}}{2}+\frac{2\pi}{3}+C.\]

Imponendo la condizione, si ottiene immediatamente: \(C=0\).

• Dominio: Tutto \(\mathbb{R}\).
• Segno: La funzione è sempre positiva (\(f(x) > 0\)) perché sia \((x^2+1)\) che \(e^{x+1}\) sono sempre maggiori di zero.
• Intersezioni: Non interseca l'asse \(x\). Interseca l'asse \(y\) in \((0, e)\).
• Asintoti:
  • Per \(x \to -\infty\), \(f(x) \to 0^+\). L'asse \(x\) (\(y=0\)) è un asintoto orizzontale.
  • Per \(x \to +\infty\), \(f(x) \to +\infty\). Non ci sono asintoti obliqui.
• Monotonia: La derivata è \(f'(x) = (x+1)^2 e^{x+1}\). Poiché \(f'(x) \ge 0\), la funzione è sempre crescente. In \(x=-1\) c'è un punto di flesso a tangente orizzontale.
• Flessi: Studiando la derivata seconda \(f''(x) = (x^2+4x+3)e^{x+1}\), troviamo due punti di flesso in:
  • \(x = -3\) (cambio concavità da alto a basso)
  • \(x = -1\) (cambio concavità da basso a alto)

Per calcolare l'integrale \(\int (x^2+1)e^{x+1}\,dx\), applichiamo l'integrazione per parti due volte:

1° passaggio:

\[\int (x^2+1)e^{x+1}\,dx = (x^2+1)e^{x+1} - \int 2x e^{x+1}\,dx\]

2° passaggio (sull'ultimo integrale):

\[= (x^2+1)e^{x+1} - \left[2xe^{x+1} - \int 2e^{x+1}\,dx\right]\]

Imponiamo la condizione al limite per \(x \to -\infty\):

\[\lim_{x\to -\infty} \left[ e^{x+1}(x^2 - 2x + 3) + C \right] = 1\]

Poiché il termine con l'esponenziale tende a \(0\), otteniamo:

\(0 + C = 1 \implies C = 1\)

Dominio: La radice quadrata richiede l'argomento non negativo: \(x \ge 0\), ovvero \([0, +\infty)\).

Intersezioni con gli assi:

• Asse \(y\): \(f(0) = 0\). Punto \((0, 0)\).
• Asse \(x\): Risolvendo \(-2x+8\sqrt{x} = 0 \implies 2\sqrt{x}(\sqrt{x}-4) = 0\), otteniamo \(x=0\) e \(x=16\).

Segno: La funzione è positiva nell'intervallo \((0, 16)\) e negativa per \(x > 16\).

Limite per \(x \to +\infty\): \[\lim_{x \to +\infty} (-2x+8\sqrt{x}) = -\infty\] (Non ci sono asintoti orizzontali o obliqui).

Derivata prima e Massimi:

\(f'(x) = -2 + \frac{4}{\sqrt{x}}\)

La funzione cresce in \([0, 4]\) e decresce in \([4, +\infty)\).
Il punto di massimo assoluto è \((4, 8)\).
Nota: in \(x=0\) la derivata tende a \(+\infty\), quindi c'è una semitangente verticale.

Derivata seconda:

\(f''(x) = -\frac{2}{x\sqrt{x}}\). Essendo sempre negativa nel dominio, la funzione è sempre concava (concavità verso il basso).

Applichiamo la proprietà di linearità dividendo l'integrale:

Calcoliamo i due pezzi:

• \(-2\int x\,dx = -2 \cdot \frac{x^2}{2} = -x^2\)
• \(8\int x^{1/2}\,dx = 8 \cdot \frac{x^{3/2}}{3/2} = 8 \cdot \frac{2}{3}x\sqrt{x} = \frac{16}{3}x\sqrt{x}\)

• Tipo di curva: Si tratta di un'iperbole non equilatera (funzione razionale fratta con grado del numeratore 2 e grado del denomonatore 1).
• Dominio: Il denominatore deve essere diverso da zero: \(2x-1 \neq 0 \implies \mathbf{x \neq \frac{1}{2}}\).
• Intersezioni:
  • Asse \(y\): Sostituendo \(x=0\) otteniamo \((0, 1)\).
  • Asse \(x\): Risolvendo \(2x^2+2x-1=0\) otteniamo \(x = \frac{-1 \pm \sqrt{3}}{2}\).
• Asintoti:
  • Verticale: \(x = \frac{1}{2}\).
  • Obliquo: Eseguendo la divisione tra polinomi si ottiene la retta \(y = x + \frac{3}{2}\).

Monotonia (Derivata prima):

\[f'(x) = \frac{4x(x-1)}{(2x-1)^2}\]

La funzione ha un massimo relativo in \((0, 1)\) e un minimo relativo in \((1, 3)\).

1. Scomposizione della funzione:

Dalla divisione polinomiale effettuata per l'asintoto obliquo, riscriviamo la funzione come:

2. Integrazione indefinita:

Calcoliamo l'integrale termine a termine:

\[\int f(x)\,dx = \int x\,dx + \int \frac{3}{2}\,dx + \int \frac{1}{2(2x-1)}\,dx\]

3. Ricerca della costante \(C\):

Imponiamo il passaggio per il punto \(\left(1, \frac{17}{8}\right)\):

\[F(1) = \frac{1}{2} + \frac{3}{2} + \frac{1}{4}\ln(1) + C = \frac{17}{8}\] \[2 + 0 + C = \frac{17}{8} \implies C = \frac{17}{8} - 2 = \mathbf{\frac{1}{8}}\]

Per definizione, la funzione Costo Totale \(C(x)\) è la primitiva del costo marginale:

Ricerca della costante (Costi Fissi):

I costi fissi rappresentano la spesa quando la produzione è zero: \(C(0) = 200\).

\[5(0) - 0{,}01(0)^2 + c = 200 \implies \mathbf{c = 200}\]

1. Costo totale per 300 kg:

Sostituiamo \(x = 300\) nella funzione appena trovata:

\[C(300) = -0{,}01(300)^2 + 5(300) + 200\] \[C(300) = -900 + 1500 + 200 = \mathbf{800}\]

Il costo totale per produrre 300 kg è di € 800.

2. Costo unitario medio (\(C_m\)):

Il costo medio è il rapporto tra il costo totale e la quantità prodotta:

Integriamo la funzione del profitto marginale:

Ricerca della costante: Sappiamo che \(P(0) = -1500\).
Sostituendo: \(40(0) - 0{,}05(0)^2 + c = -1500 \implies \mathbf{c = -1500}\).

Il profitto è massimo quando la sua derivata (il profitto marginale) è nulla:

\[40 - 0{,}1x = 0 \implies 0{,}1x = 40 \implies \mathbf{x = 400}\]

Calcoliamo il valore del profitto massimo per 400 pezzi:

\[P(400) = -0{,}05(400)^2 + 40(400) - 1500 = -8000 + 16000 - 1500 = \mathbf{6500}\]

Risolviamo l'equazione di secondo grado \(P(x) = 0\):

\[-0{,}05x^2 + 40x - 1500 = 0\]

Utilizzando la formula risolutiva, otteniamo i due valori critici:

• \(x_1 \approx 40\): Soglia minima di produzione per iniziare a guadagnare.
• \(x_2 \approx 760\): Soglia massima oltre la quale i costi superano i ricavi.

Scomponiamo il denominatore: \(x^2 - 5x + 6 = (x-2)(x-3)\).

Cerchiamo \(A\) e \(B\) tali che: \(\frac{1}{(x-2)(x-3)} = \frac{A}{x-2} + \frac{B}{x-3}\)

Risolvendo il sistema otteniamo \(A = -1\) e \(B = 1\).

Il denominatore è un quadrato perfetto: \(x^2 - 6x + 9 = (x-3)^2\).

L'integrale si risolve come potenza negativa: \(\int (x-3)^{-2} \, dx\)

Completiamo il quadrato al denominatore: \(x^2 + x + 1 = (x + \frac{1}{2})^2 + \frac{3}{4}\).

Riconduciamo alla forma standard dell'arcotangente \(\int \frac{1}{u^2+1}du\).

Scomponiamo in fratti semplici: \(\frac{2x - 1}{(x-1)(x-3)} = \frac{A}{x-1} + \frac{B}{x-3}\)

Si ottiene \(A = -1/2\) e \(B = 5/2\).

1. Divisione polinomiale:

Poiché il grado del numeratore (2) è maggiore di quello del denominatore (1), eseguiamo la divisione:

• Quoziente: \(Q(x) = x + 2\)
• Resto: \(R = 3\)

Riscriviamo la frazione come \(Q(x) + \frac{R}{D(x)}\):

2. Integrazione:

\[\int (x + 2) \, dx + \int \frac{3}{x+1} \, dx\]

Strategia rapida: Scomposizione per raccoglimento

Invece della divisione lunga, notiamo che al numeratore possiamo fare un raccoglimento parziale:

Semplificando il termine \((x^2 + 1)\) presente anche al denominatore, l'integrale diventa semplicissimo:

\[\int \frac{(x^2 + 1)(x + 2)}{x^2 + 1} \, dx = \int (x + 2) \, dx\]