

Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.


Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
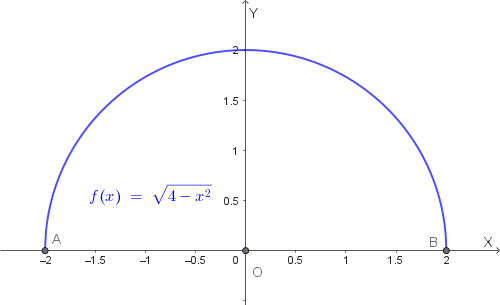
Si consideri la funzione \[ f(x)=\sqrt{4-x^2}. \]
a) Studiare la funzione e rappresentarla graficamente.
b) Trovare la più generale primitiva di \(f(x)\), dettagliando i calcoli necessari per determinarla, e individuare quella che passa per il punto di coordinate \(\left(\sqrt{3},\,\frac{\sqrt{3}}{2}+\frac{2\pi}{3}\right)\).
Soluzione quesito 2:
La funzione è definita quando il radicando è non negativo:
\[ 4-x^2 \ge 0 \quad \Rightarrow \quad -2 \le x \le 2 \]Il dominio è quindi: \[ D_f = [-2,2]. \]
Poiché \[ f(-x)=\sqrt{4-(-x)^2}=\sqrt{4-x^2}=f(x), \] la funzione è pari e il grafico è simmetrico rispetto all’asse \(y\).
Le intersezioni con gli assi sono:
Elevando al quadrato l’equazione \(y=\sqrt{4-x^2}\) si ottiene: \[ x^2+y^2=4, \] che rappresenta una circonferenza di centro l’origine e raggio 2. Poiché \(y \ge 0\), il grafico della funzione è la semicirconferenza superiore.
Grafico della funzione:
Calcoliamo l’integrale:
\[ \int \sqrt{4-x^2}\,dx \]Utilizziamo una sostituzione trigonometrica ponendo:
\[ x = 2\sin t \quad \Rightarrow \quad dx = 2\cos t\,dt. \]Si ha:
\[ \sqrt{4-x^2} = \sqrt{4-4\sin^2 t}=2\cos t. \]L’integrale diventa quindi:
\[ \int 2\cos t \cdot 2\cos t\,dt =4\int \cos^2 t\,dt. \]Ricordando che:
\[ \cos^2 t = \frac{1+\cos 2t}{2}, \]otteniamo:
\[ 4\int \frac{1+\cos 2t}{2}\,dt =2\int (1+\cos 2t)\,dt. \] \[ =2\left(t+\frac{\sin 2t}{2}\right)+C =2t+\sin 2t+C. \]Tornando alla variabile \(x\), si osserva che:
\[ t=\arcsin\!\left(\frac{x}{2}\right), \quad \sin 2t = 2\sin t\cos t = \frac{x}{2}\sqrt{4-x^2}. \]Si ottiene quindi la primitiva generale:
\[ F(x)=\frac{x}{2}\sqrt{4-x^2} +2\arcsin\!\left(\frac{x}{2}\right)+C. \]La primitiva deve passare per il punto di coordinate \(\left(\sqrt{3},\,\frac{\sqrt{3}}{2}+\frac{2\pi}{3}\right)\). Calcoliamo quindi \(F(\sqrt{3})\).
Poiché:
\[ \sqrt{4-(\sqrt{3})^2}=1, \quad \arcsin\!\left(\frac{\sqrt{3}}{2}\right)=\frac{\pi}{3}, \]risulta:
\[ F(\sqrt{3}) =\frac{\sqrt{3}}{2} +2\cdot\frac{\pi}{3} +C =\frac{\sqrt{3}}{2}+\frac{2\pi}{3}+C. \]Imponendo la condizione:
\[ F(\sqrt{3})=\frac{\sqrt{3}}{2}+\frac{2\pi}{3}, \]si ottiene immediatamente:
\[ C=0. \]Conclusione:
La primitiva richiesta è:
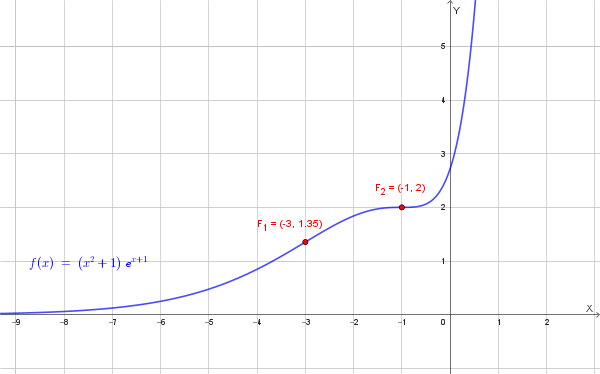
\[ F(x)=\frac{x}{2}\sqrt{4-x^2} +2\arcsin\!\left(\frac{x}{2}\right). \]a) Studiare la funzione \[ f(x)=(x^2+1)e^{x+1} \] e rappresentarla graficamente.
b) Trovare la più generale primitiva \(F(x)\) di \(f(x)\) tale che: \[ \lim_{x\to -\infty} F(x)=1. \]
Soluzione quesito 2:
Per studiare la funzione, analizziamo i seguenti aspetti:
Per verificare se la funzione è pari o dispari, calcoliamo \(f(-x)\):
\[ f(-x) = ((-x)^2+1)e^{-x+1} = (x^2+1)e^{-x+1} \]
Poiché \(f(-x) \neq f(x)\) e \(f(-x) \neq -f(x)\), la funzione \(f(x)\) **non è né pari né dispari**.
\[ \lim_{x \to -\infty} (x^2+1)e^{x+1} \]
Quando \(x \to -\infty\), \(x^2+1 \to +\infty\) e \(e^{x+1} \to 0\). Questa è una forma indeterminata del tipo \(\infty \cdot 0\).
Possiamo riscrivere il limite e concentrarci sui termini che causano l'indeterminazione, notando che \(e^{x+1} = e^x \cdot e\):
\[ e \cdot \lim_{x \to -\infty} (x^2+1)e^{x} = e \cdot \lim_{x \to -\infty} \frac{x^2+1}{e^{-x}} \]
Per il **confronto tra infiniti**, sappiamo che l'esponenziale \(e^{-x}\) (per \(x \to -\infty\), \( -x \to +\infty\)) tende a infinito molto più velocemente di qualsiasi potenza di \(x\) (in questo caso \(x^2+1\)). Questo significa che il denominatore "domina" il numeratore.
Pertanto, il limite è:
\[ \lim_{x \to -\infty} (x^2+1)e^{x+1} = 0^+ \]
Il risultato è \(0^+\) perché la funzione è sempre positiva, quindi si avvicina a 0 da valori positivi.
\[ \lim_{x \to +\infty} (x^2+1)e^{x+1} = +\infty \]
In questo caso, sia \((x^2+1)\) che \(e^{x+1}\) tendono a \(+\infty\) quando \(x \to +\infty\). Il prodotto di due infiniti positivi è \(+\infty\).
Dal limite per \(x \to -\infty\), abbiamo che \( \lim_{x \to -\infty} f(x) = 0 \). Questo significa che l'asse \(x\) (equazione \(y=0\)) è un **asintoto orizzontale** per \(x \to -\infty\).
Dal limite per \(x \to +\infty\), \( \lim_{x \to +\infty} f(x) = +\infty \). Verifichiamo la presenza di asintoti obliqui per \(x \to +\infty\):
\[ m = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{(x^2+1)e^{x+1}}{x} = \lim_{x \to +\infty} \left( x + \frac{1}{x} \right)e^{x+1} = +\infty \]
Poiché \(m = +\infty\), **non esistono asintoti obliqui** per \(x \to +\infty\).
Non ci sono asintoti verticali, in quanto la funzione è definita su tutto \(\mathbb{R}\).
Dal punto a), per \(a=1\), abbiamo che \(f'(x) = (1 \cdot x^2+2x+1)e^{x+1} = (x+1)^2 e^{x+1}\).
Poiché \((x+1)^2 \ge 0\) e \(e^{x+1} > 0\), \(f'(x) \ge 0\) per ogni \(x\). Questo conferma che \(f(x)\) è **sempre crescente** su tutto \(\mathbb{R}\).
Si annulla solo in \(x=-1\), che è un punto di flesso a tangente orizzontale (come discusso nel punto a)).
Calcoliamo la derivata seconda di \(f(x)\):
\[ f''(x) = (x^2+4x+3)e^{x+1} \]
Studiamo il segno di \(f''(x)\) per determinare la concavità/convessità e i punti di flesso. Poiché \(e^{x+1} > 0\) per ogni \(x\), il segno di \(f''(x)\) dipende dal segno del trinomio \(P(x) = x^2+4x+3\).
Troviamo le radici di \(x^2+4x+3=0\):
\[ x = \frac{-4 \pm \sqrt{4^2 - 4 \cdot 1 \cdot 3}}{2 \cdot 1} = \frac{-4 \pm \sqrt{16 - 12}}{2} = \frac{-4 \pm 2}{2} \]
Le radici sono \(x_1 = \frac{-4-2}{2} = -3\) e \(x_2 = \frac{-4+2}{2} = -1\).
Il trinomio \(x^2+4x+3\) si può associare ad una parabola con concavità verso l'alto (coefficiente di \(x^2\) positivo), quindi è positivo esternamente alle radici e negativo tra le radici.
Schema del segno di \(f''(x)\):
Da questo schema si deduce che:
I punti in cui la concavità cambia sono **punti di flesso**.
Il grafico della funzione è il seguente:
Calcoliamo: \[ \int (x^2+1)e^{x+1}\,dx. \] Integrando per parti due volte si ottiene:
\[ \int (x^2+1)e^{x+1}\,dx =(x^2+1)e^{x+1}-\int 2x e^{x+1}\,dx \] \[ =(x^2+1)e^{x+1}-\left[2xe^{x+1}-\int 2e^{x+1}\,dx\right] \] \[ =(x^2+1)e^{x+1}-2xe^{x+1}+2e^{x+1}+C \] \[ =e^{x+1}(x^2-2x+3)+C. \]Determinazione della costante
Poiché: \[ \lim_{x\to -\infty} e^{x+1}(x^2-2x+3)=0, \] si ha: \[ \lim_{x\to -\infty}F(x)=C. \] Impostando la condizione richiesta: \[ \lim_{x\to -\infty}F(x)=1, \] segue: \[ C=1. \]
Conclusione:
La primitiva richiesta è: \[ F(x)=e^{x+1}(x^2-2x+3)+1. \]
È data la funzione di equazione:
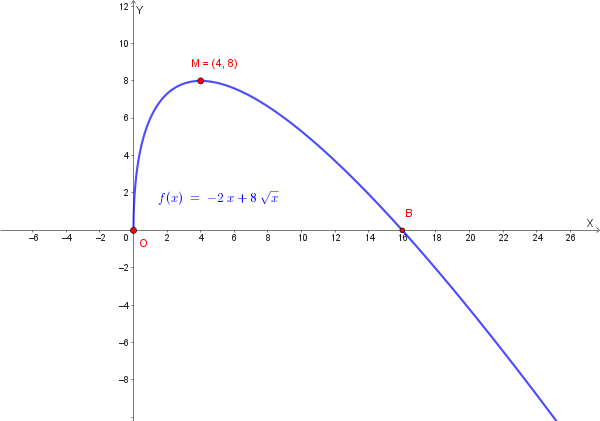
\[ f(x) = -2x + 8\sqrt{x} \]a) Studiare la funzione e rappresentarla graficamente.
b) Calcolare \(\displaystyle\int f(x)\,dx\)
Soluzione quesito 3:
La funzione da studiare è \(f(x) = -2x+8\sqrt{x}\).
La presenza del termine \(\sqrt{x}\) richiede che l'argomento della radice quadrata sia non negativo. Pertanto, il dominio è \(x \ge 0\), ovvero l'intervallo \([0, +\infty)\).
La funzione non è né pari né dispari, poiché il suo dominio \([0, +\infty)\) non è simmetrico rispetto all'origine.
Dallo studio delle intersezioni, la funzione è positiva quando \(-2x+8\sqrt{x} > 0\). Semplificando, otteniamo \(-x+4\sqrt{x} > 0\). Dividendo per \(\sqrt{x}\) (per \(x>0\)), si ha \(-\sqrt{x}+4 > 0 \implies \sqrt{x} < 4 \implies x < 16\).
La funzione è positiva in \((0, 16)\), negativa per \(x > 16\) e nulla in \(x=0\) e \(x=16\).
Dobbiamo calcolare il limite per \(x \to +\infty\):
\(\lim_{x \to +\infty} (-2x+8\sqrt{x})\). Mettendo in evidenza \(x\), si ottiene:
\(\lim_{x \to +\infty} x(-2+\frac{8}{\sqrt{x}}) = +\infty(-2+0) = -\infty\).
Dato che \(\lim_{x \to +\infty} f(x) = -\infty\), verifichiamo la presenza di un asintoto obliquo:
\(m = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{-2x+8\sqrt{x}}{x} = \lim_{x \to +\infty} (-2+\frac{8}{\sqrt{x}}) = -2\).
\(q = \lim_{x \to +\infty} [f(x)-mx] = \lim_{x \to +\infty} [-2x+8\sqrt{x} - (-2x)] = \lim_{x \to +\infty} (8\sqrt{x}) = +\infty\).
Poiché \(q\) non è un valore finito, non ci sono asintoti obliqui. La funzione non presenta asintoti.
\(f'(x) = -2 + \frac{8}{2\sqrt{x}} = -2 + \frac{4}{\sqrt{x}}\).
Il dominio della derivata prima è \(x > 0\), poiché il termine \(\sqrt{x}\) non può essere nullo al denominatore.
Per studiare il tipo di non derivabilità in \(x=0\), calcoliamo il limite della derivata prima per \(x\) che tende a \(0\) da destra:
\(\lim_{x \to 0^+} f'(x) = \lim_{x \to 0^+} \left(-2 + \frac{4}{\sqrt{x}}\right) = -2 + \frac{4}{0^+} = -2 + (+\infty) = +\infty\).
Poiché il limite della derivata prima per \(x \to 0^+\) è infinito, la funzione non è derivabile in \(x=0\). In questo punto, la funzione ha una semitangente verticale.
Studiamo il segno di \(f'(x) = -2 + \frac{4}{\sqrt{x}}\). Poniamo \(f'(x) > 0\):
\(-2 + \frac{4}{\sqrt{x}} > 0 \implies \frac{4}{\sqrt{x}} > 2 \implies \sqrt{x} < 2 \implies x < 4\).
Ricordando che il dominio è \(x \ge 0\), la derivata prima è positiva in \([0, 4)\) e negativa in \((4, +\infty)\).
Questo ci dice che la funzione cresce in \([0, 4]\) e decresce in \([4, +\infty)\).
Per \(x=4\) la derivata si annulla, e il segno cambia da positivo a negativo, quindi in \(x=4\) si ha un punto di massimo assoluto.
Il valore del massimo è \(f(4) = -2(4)+8\sqrt{4} = -8+16=8\), quindi il punto di massimo è \((4,8)\).
Calcoliamo la derivata seconda di \(f(x)\):
\(f''(x) = \frac{d}{dx} \left(-2 + 4x^{-\frac{1}{2}}\right) = 0 + 4 \left(-\frac{1}{2}\right)x^{-\frac{3}{2}} = -2x^{-\frac{3}{2}} = -\frac{2}{x\sqrt{x}}\).
Il segno di \(f''(x) = -\frac{2}{x\sqrt{x}}\) è sempre negativo per ogni \(x\) nel dominio \((x > 0)\).
Questo significa che la funzione ha concavità rivolta verso il basso in tutto il suo dominio \((0, +\infty)\). Non ci sono punti di flesso.
Il grafico della funzione è quindi:
Dobbiamo calcolare:
\[ \int f(x)\,dx = \int (-2x + 8\sqrt{x})\,dx \]Separiamo l'integrale in due parti:
\[ \int (-2x + 8\sqrt{x})\,dx = \int (-2x)\,dx + \int 8\sqrt{x}\,dx \]Riscriviamo \(\sqrt{x} = x^{1/2}\):
\[ \int 8\sqrt{x}\,dx = \int 8x^{1/2}\,dx = 8 \cdot \frac{x^{1/2+1}}{1/2+1} = 8 \cdot \frac{x^{3/2}}{3/2} = 8 \cdot \frac{2}{3}x^{3/2} = \frac{16}{3}x^{3/2} \]\[ \int (-2x + 8\sqrt{x})\,dx = -x^2 + \frac{16}{3}x^{3/2} + C = -x^2 + \frac{16}{3}x\sqrt{x} + C \]
È data la funzione di equazione:
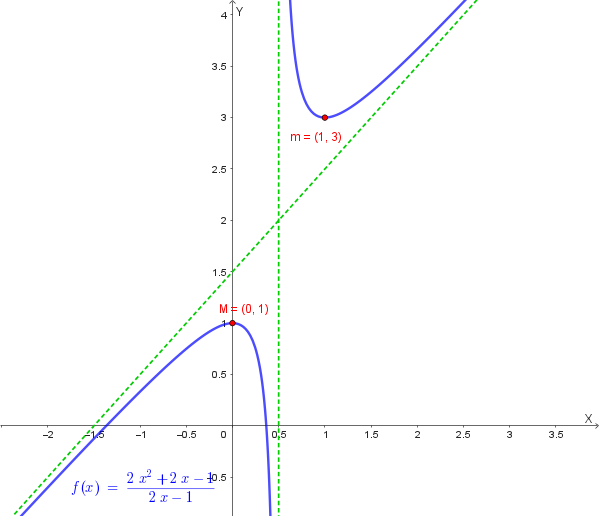
\[ f(x) = \frac{2x^2+2x-1}{2x-1} \]a) Studiare la funzione e rappresentarla graficamente.
b) Trovare la primitiva \(F(x)\) di \(f(x)\) che passa per il punto di coordinate \(\left(1, \frac{17}{8}\right)\).
Soluzione quesito 4:
La funzione da studiare è \[\displaystyle f(x) = \frac{2x^2+2x-1}{2x-1}\]
Osservazione preliminare: Riscrivendo la funzione nella forma \(F(x,y)=0\), otteniamo l'equazione \(2x^2 - 2xy + 2x + y - 1 = 0\). Il discriminante della conica è \(\Delta = B^2 - 4AC = (-2)^2 - 4(2)(0) = 4 > 0\). Poiché \(\Delta > 0\), questa equazione rappresenta un'iperbole. La presenza di un asintoto obliquo e di un asintoto verticale conferma la sua natura.
Il denominatore deve essere diverso da zero: \(2x-1 \neq 0 \implies x \neq \frac{1}{2}\).
Il dominio è \(D = \mathbb{R} \setminus \left\{\frac{1}{2}\right\}\).
Il dominio non è simmetrico rispetto all'origine, quindi la funzione non è né pari né dispari.
La funzione è positiva quando numeratore (\(N\)) e denominatore (\(D\)) hanno lo stesso segno. Studiamo separatamente il segno dei due termini.
Riportiamo i segni sulla seguente tabella (i punti critici, in ordine, sono \(x_1 \approx -1.366\), \(x_2 \approx 0.366\), e \(x_A = 0.5\)):
| Intervallo | \(x < \frac{-1 - \sqrt{3}}{2}\) | \(\frac{-1 - \sqrt{3}}{2} < x < \frac{-1 + \sqrt{3}}{2}\) | \(\frac{-1 + \sqrt{3}}{2} < x < \frac{1}{2}\) | \(x > \frac{1}{2}\) |
|---|---|---|---|---|
| Numeratore (\(N\)) | \(+\) | \(-\) | \(+\) | \(+\) |
| Denominatore (\(D\)) | \(-\) | \(-\) | \(-\) | \(+\) |
| Segno \(f(x)\) (\(N/D\)) | \(-\) | \(+\) | \(-\) | \(+\) |
La funzione ha dominio \(D = \mathbb{R} \setminus \left\{\frac{1}{2}\right\}\). Calcoliamo i limiti agli estremi del dominio.
Come verificato nel punto a), la retta \(x = \frac{1}{2}\) è l'Asintoto Verticale.
Come determinato nel punto a), l'equazione dell'asintoto obliquo è:
\[y = x + \frac{3}{2}\]Non ci sono asintoti orizzontali, poiché \(\lim_{x \to \pm\infty} f(x) = \pm\infty\).
Calcoliamo la derivata prima \(f'(x)\):
\[f'(x) = \frac{4x^2-4x}{(2x-1)^2} = \frac{4x(x-1)}{(2x-1)^2}\]Studiamo il segno di \(f'(x) > 0\). Il numeratore è positivo per \(x < 0\) oppure \(x > 1\).
Punti di estremo:
Ricalcoliamo la derivata seconda a partire dalla derivata prima \(f'(x) = \frac{4x^2-4x}{(2x-1)^2}\):
\[f''(x) = \frac{(8x-4)(2x-1)^2 - (4x^2-4x) \cdot 4(2x-1)}{(2x-1)^4}\]Semplificando e raccogliendo \(4(2x-1)\) al numeratore, si ottiene:
\[f''(x) = \frac{4}{(2x-1)^3}\]Studiamo il segno di \(f''(x)\): esso dipende unicamente dal denominatore \( (2x-1)^3 \), che ha lo stesso segno di \(2x-1\).
Il cambio di concavità avviene solo in corrispondenza dell'asintoto verticale \(x = \frac{1}{2}\). Pertanto, la funzione non presenta punti di flesso.
Il grafico della funzione è quindi il seguente:
Dobbiamo trovare la primitiva \(F(x)\) di \(f(x) = \frac{2x^2+2x-1}{2x-1}\) che passa per il punto \(\left(1, \frac{17}{8}\right)\).
Eseguiamo la divisione tra il numeratore \(2x^2+2x-1\) e il denominatore \(2x-1\):
Dividendo \(2x^2\) per \(2x\) otteniamo \(x\):
\[2x^2 + 2x - 1 = (2x-1) \cdot x + (2x + x - 1) = (2x-1) \cdot x + (3x - 1)\]Continuando, dividendo \(3x\) per \(2x\) otteniamo \(\frac{3}{2}\):
\[3x - 1 = (2x-1) \cdot \frac{3}{2} + \left(-1 + \frac{3}{2}\right) = (2x-1) \cdot \frac{3}{2} + \frac{1}{2}\]Quindi:
\[f(x) = \frac{2x^2+2x-1}{2x-1} = x + \frac{3}{2} + \frac{1/2}{2x-1} = x + \frac{3}{2} + \frac{1}{2(2x-1)}\]Calcoliamo ora l'integrale indefinito:
\[ \int f(x)\,dx = \int \left(x + \frac{3}{2} + \frac{1}{2(2x-1)}\right)dx \]Separiamo gli integrali:
\[ = \int x\,dx + \int \frac{3}{2}\,dx + \int \frac{1}{2(2x-1)}\,dx \]Calcoliamo ciascun integrale:
Quindi l'integrale generale è:
\[ F(x) = \frac{x^2}{2} + \frac{3}{2}x + \frac{1}{4}\ln|2x-1| + C \]Imponiamo la condizione \(F(1) = \frac{17}{8}\):
\[ F(1) = \frac{1^2}{2} + \frac{3}{2}(1) + \frac{1}{4}\ln|2(1)-1| + C = \frac{17}{8} \] \[ \frac{1}{2} + \frac{3}{2} + \frac{1}{4}\ln(1) + C = \frac{17}{8} \] \[ \frac{1}{2} + \frac{3}{2} + 0 + C = \frac{17}{8} \] \[ 2 + C = \frac{17}{8} \] \[ C = \frac{17}{8} - 2 = \frac{17}{8} - \frac{16}{8} = \frac{1}{8} \]La primitiva richiesta è: \[ F(x) = \frac{x^2}{2} + \frac{3}{2}x + \frac{1}{4}\ln|2x-1| + \frac{1}{8} \]
Verifica: Controlliamo che \(F(1) = \frac{17}{8}\):
\[ F(1) = \frac{1}{2} + \frac{3}{2} + \frac{1}{4}\ln(1) + \frac{1}{8} = 2 + 0 + \frac{1}{8} = \frac{17}{8} \quad \checkmark \]Il costo totale per la produzione di una quantità \(x\) di un certo prodotto è espresso dalla funzione \(C(x)\). La sua derivata \(C'(x)\) è detta costo marginale e rappresenta il costo che un'impresa deve sostenere per produrre un'unità di prodotto in più, ovvero la variazione nei costi totali che si verifica quando varia di una unità la quantità prodotta.
Un caseificio sa che il costo marginale della sua produzione, in euro al kilogrammo, è espresso dalla funzione: \(C'(x) = 5 - 0,02x\), per \(x \leq 400\) kg.
a) Scrivere la funzione costo totale, sapendo che i costi fissi sono di € 200.
b) Trovare il costo totale per produrre 300 kg di formaggio e il costo unitario medio.
Soluzione Quesito 5
Poiché il costo marginale è la derivata del costo totale, per ricavare \(C(x)\) procediamo con l'integrazione:
\[ C(x) = \int C'(x) \, dx = \int (5 - 0,02x) \, dx \] \[ C(x) = 5x - 0,02 \frac{x^2}{2} + c = 5x - 0,01x^2 + c \]I costi fissi rappresentano il costo quando la produzione è nulla (\(x = 0\)). Quindi \(C(0) = 200\):
\[ 5(0) - 0,01(0)^2 + c = 200 \implies c = 200 \]La funzione costo totale è: \(C(x) = -0,01x^2 + 5x + 200\).
Costo totale per 300 kg:
\[ C(300) = -0,01(300)^2 + 5(300) + 200 = -900 + 1.500 + 200 = 800 \]Il costo totale è di € 800.
Costo unitario medio:
Il costo medio si ottiene dividendo il costo totale per la quantità prodotta (\(C(x)/x\)):
\[ C_m = \frac{800}{300} \approx 2,67 \]Il costo unitario medio è di circa € 2,67 al kg.
Il profitto marginale di un'azienda che produce componenti elettronici è descritto dalla funzione \(P'(x)\), che indica la rapidità con cui il profitto totale \(P(x)\) varia al variare del numero di pezzi \(x\) venduti:
\[ P'(x) = 40 - 0,1x \]dove \(x\) è il numero di componenti e il profitto è espresso in euro.
a) Ricavare la funzione del profitto totale \(P(x)\), sapendo che l'azienda sostiene costi fissi iniziali tali per cui, a vendite nulle (\(x = 0\)), si registra una perdita di € 1.500.
b) Determinare il punto di massimo profitto, ovvero la quantità \(x\) di pezzi da vendere per massimizzare il guadagno, e il valore di tale profitto.
c) Determinare i punti di pareggio (break-even points), ovvero i valori di \(x\) per cui il profitto totale è nullo (\(P(x) = 0\)).
Soluzione quesito 6:
Poiché il profitto marginale è la derivata del profitto totale, integriamo \(P'(x)\):
\[ P(x) = \int (40 - 0,1x) \, dx = 40x - 0,1 \frac{x^2}{2} + c = -0,05x^2 + 40x + c \]Imponendo la condizione \(P(0) = -1500\):
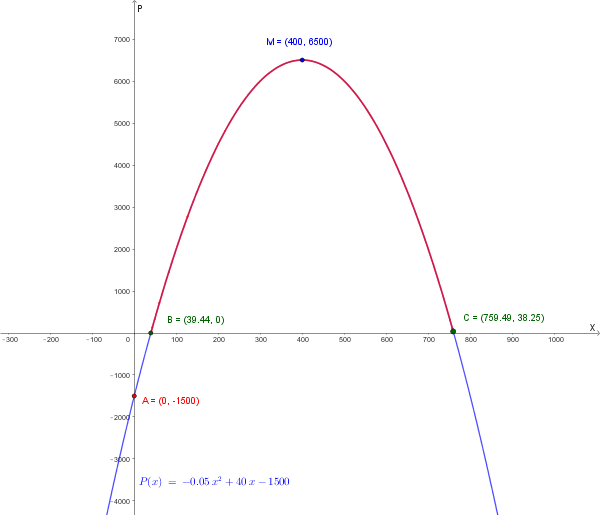
\[ -0,05(0)^2 + 40(0) + c = -1500 \implies c = -1500 \]La funzione profitto totale è: \(P(x) = -0,05x^2 + 40x - 1500\)
Il massimo profitto si ha quando la derivata prima (il profitto marginale) è nulla:
\[ P'(x) = 0 \implies 40 - 0,1x = 0 \implies 0,1x = 40 \implies x = 400 \]Il valore del profitto massimo è:
\[ P(400) = -0,05(400)^2 + 40(400) - 1500 = -8000 + 16000 - 1500 = 6500 \]L'azienda ottiene il massimo profitto vendendo 400 componenti, con un guadagno di € 6.500.
Risolviamo \(P(x) = 0\): \(-0,05x^2 + 40x - 1500 = 0\). Moltiplicando per \(-20\):
\[ x^2 - 800x + 30000 = 0 \] \[ x = \frac{800 \pm \sqrt{640000 - 120000}}{2} = \frac{800 \pm \sqrt{520000}}{2} \approx \frac{800 \pm 721,1}{2} \]L'equazione ammette due soluzioni distinte, indicando due punti di pareggio:
Grafico della funzione Profitto
Si calcolino i seguenti integrali indefiniti di funzioni razionali fratte con denominatore di secondo grado:
a) \(\displaystyle \int \frac{1}{x^2 - 5x + 6} \, dx \quad \)
b) \(\displaystyle \int \frac{1}{x^2 - 6x + 9} \, dx \quad \)
c) \(\displaystyle \int \frac{1}{x^2 + x + 1} \, dx \quad \)
d) \(\displaystyle \int \frac{2x - 1}{x^2 - 4x + 3} \, dx \quad \)
Soluzione quesito 7:
Il denominatore \(x^2 - 5x + 6\) si scompone in \((x-2)(x-3)\). Utilizziamo il metodo dei fratti semplici:
\[ \frac{1}{(x-2)(x-3)} = \frac{A}{x-2} + \frac{B}{x-3} \]Risolvendo il sistema si ottiene \(A = -1\) e \(B = 1\). L'integrale diventa:
\[ \int \left( \frac{-1}{x-2} + \frac{1}{x-3} \right) dx = -\ln|x-2| + \ln|x-3| + c = \ln\left| \frac{x-3}{x-2} \right| + c \]Il denominatore è un quadrato perfetto: \(x^2 - 6x + 9 = (x-3)^2\). L'integrale si risolve come potenza negativa:
\[ \int (x-3)^{-2} \, dx = \frac{(x-3)^{-1}}{-1} + c = -\frac{1}{x-3} + c \]Poiché il denominatore \(x^2 + x + 1\) non è scomponibile (\(\Delta = -3\)), completiamo il quadrato per ricondurci alla forma dell'arcotangente:
\[ x^2 + x + 1 = \left(x + \frac{1}{2}\right)^2 + \frac{3}{4} \]L'integrale diventa:
\[ \int \frac{1}{\left(x + \frac{1}{2}\right)^2 + \frac{3}{4}} \, dx = \frac{4}{3} \int \frac{1}{\frac{4}{3}\left(x + \frac{1}{2}\right)^2 + 1} \, dx = \frac{4}{3} \int \frac{1}{\left(\frac{2x+1}{\sqrt{3}}\right)^2 + 1} \, dx \]Effettuando la sostituzione o applicando la formula diretta:
\[ \frac{4}{3} \cdot \frac{\sqrt{3}}{2} \arctan\left(\frac{2x+1}{\sqrt{3}}\right) + c = \frac{2}{\sqrt{3}} \arctan\left(\frac{2x+1}{\sqrt{3}}\right) + c \]Scomponiamo il denominatore: \(x^2 - 4x + 3 = (x-1)(x-3)\). Usiamo i fratti semplici:
\[ \frac{2x - 1}{(x-1)(x-3)} = \frac{A}{x-1} + \frac{B}{x-3} \]Per \(x=1 \implies A = \frac{2(1)-1}{1-3} = -\frac{1}{2}\). Per \(x=3 \implies B = \frac{2(3)-1}{3-1} = \frac{5}{2}\).
\[ \int \left( \frac{-1/2}{x-1} + \frac{5/2}{x-3} \right) dx = -\frac{1}{2}\ln|x-1| + \frac{5}{2}\ln|x-3| + c \]Si calcolino i seguenti integrali indefiniti di funzioni razionali fratte in cui il numeratore ha grado maggiore del denominatore. (Per integrali di questo tipo si usa la divisione tra polinomi prima di integrare.)
a) \(\displaystyle \int \frac{x^2 + 3x + 5}{x + 1} \, dx\)
b) \(\displaystyle \int \frac{x^3 + 2x^2 + x + 2}{x^2 + 1} \, dx\)
Soluzione quesito 8:
Risultati finali:
a) \(\displaystyle \int \frac{x^2 + 3x + 5}{x + 1}\,dx = \frac{x^2}{2} + 2x + 3\ln|x+1| + c\)
b) \(\displaystyle \int \frac{x^3 + 2x^2 + x + 2}{x^2 + 1}\,dx = \frac{x^2}{2} + 2x + c\)