Maturità sperimentale 1996-97

l. In un piano riferito ad un sistema di assi cartesiani ortogonali Oxy sia data la parabola di equazione y=x² e sia P un suo punto di ascissa ed r la parallela per P all'asse y.

Siano le parabole con asse la retta r, vertice in P e stessa distanza focale di (distanza fuoco-direttrice, pari a per la parabola di equazione y=ax²+bx+c).

Il candidato:

a) scriva in funzione di le equazioni di , essendo la parabola che incontra solo in P;

b) scriva le equazioni delle trasformazioni che mutano in e in ;

c) dica la natura di dette trasformazioni precisando se si tratta di trasformazioni dirette o inverse e se hanno elementi che si trasformano in se stessi;

d) fissato e dette T, T₁, T₂ le rispettive intersezioni di , con la retta di equazione x-h=0, studi la funzione 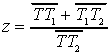al variare di h, e se ne tracci il relativo grafico in un piano riferito ad un sistema di assi cartesiani ortogonali O'hz.

2. In un piano riferito ad un sistema di assi cartesiani ortogonali Oxy sia r la retta di equazione x-1=0 e P un suo punto. Siano A e B i punti d'intersezione della retta OP con la circonferenza di centro P e raggio .

Il candidato:

a) verifichi che il luogo di A e B, al variare del punto P su r, è dato dalle curve rispettivamente di equazione y=f₁(x) e y=f₂(x), essendo:

b) determini l'insieme E di esistenza della funzione f₁(x), gli insiemi in cui essa assume valore positivo, negativo o nullo, gli eventuali asintoti, il valore x₀ in cui ha un massimo relativo, e dimostri che le tangenti a nei punti le cui ascisse sono gli estremi di E nei quali f₁(x) è definita, sono parallele all'asse y;

c) disegni la curva e, quindi, la curva ;

d) detta t la tangente alla curva , nel suo punto M(x_0, f(x₀)) determini l'ulteriore intersezione di t con ;

e) detta S l'area della regione finita di piano compresa tra , l'asse delle x e la parallela all'asse y per il punto M, descriva una procedura che consenta di calcolare, mediante un metodo d'integrazione numerica a sua scelta, i valori approssimati di S e la codifichi in un linguaggio di programmazione conosciuto.

3. Si consideri in un piano un rettangolo ABCD i cui lati BC ed AB misurano rispettivamente a e 2a. Sia AEF, con , un triangolo isoscele la cui base AE ha misura 2r.

Il candidato:

a) dimostri che una retta s parallela ad AB, a distanza x da essa, interseca i triangoli AEF ed AEC secondo segmenti uguali;

b) detta C₁ la circonferenza di diametro AE e appartenente al piano passante per AB e perpendicolare ad , e detti T₁ e T₂ i coni di base C₁ e vertici rispettivamente nei punti F e C, dimostri che le sezioni C₁' e C₂' di detti coni con il piano , passante per la retta s e parallelo al piano , sono circonferenze;

c) determini i volumi dei coni T₁ e T₂;

d) determini, per via sintetica o analitica, il valore di x per il quale C'₁ e C'₂ sono tangenti esternamente.

______________________________________________________

La prova richiede lo svolgimento di due soli problemi, scelti tra quelli proposti.

SOLUZIONI