Definizione del Differenziale di una Funzione
Sia \( y = f(x) \) una funzione derivabile in un punto \( x \). Il differenziale della funzione \( f \) nel punto \( x \), corrispondente a un incremento \( \Delta x \) della variabile indipendente, è definito come:
Dove:
- \( dy \) (o \( df \)) rappresenta il differenziale della funzione
- \( f'(x) \) è la derivata della funzione nel punto \( x \)
- \( \Delta x \) è l'incremento della variabile indipendente
Notazione: perché scriviamo \( dx \) al posto di \( \Delta x \)?
La notazione con \( dx \) deriva da una considerazione particolare. Consideriamo la funzione identità \( y = f(x) = x \).
Per la funzione \( y = x \), la derivata è \( f'(x) = 1 \).
Applicando la definizione di differenziale:
Quindi, per la funzione identità, il differenziale coincide con l'incremento: \( dy = \Delta x \).
Poiché per \( y = x \) abbiamo \( dy = \Delta x \), possiamo indicare l'incremento \( \Delta x \) con il simbolo \( dx \), cioè il differenziale della variabile indipendente.
Di conseguenza, la formula del differenziale può essere scritta in modo più compatto come:
Questa notazione è universalmente utilizzata in matematica e mette in evidenza il legame tra differenziale e derivata.
Dalla definizione del differenziale \( dy = f'(x) \cdot dx \), possiamo ricavare la derivata dividendo entrambi i membri per \( dx \) (con \( dx \neq 0 \)):
Questa è la celebre notazione di Leibniz per la derivata, introdotta dal matematico tedesco Gottfried Wilhelm Leibniz (1646-1716), uno dei fondatori del calcolo infinitesimale insieme a Isaac Newton.
La notazione \( \frac{dy}{dx} \) rappresenta la derivata come rapporto di differenziali e ha un profondo significato geometrico: esprime il tasso di variazione istantaneo di \( y \) rispetto a \( x \).
Quindi possiamo scrivere equivalentemente:
Questa notazione è estremamente potente e intuitiva, ed è ampiamente utilizzata in fisica, ingegneria e in tutte le scienze applicate per rappresentare velocità di cambiamento e relazioni tra grandezze variabili.
Esempi di calcolo del differenziale
Esempio 1: Differenziale in un punto generico
Calcolare il differenziale della funzione \( f(x) = x^2 \) in un punto generico \( x \).
Calcoliamo la derivata: \( f'(x) = 2x \)
Il differenziale è:
Esempio 2: Differenziale in un punto specifico
Calcolare il differenziale della funzione \( f(x) = x^3 - 2x \) nel punto \( x_0 = 2 \).
Calcoliamo la derivata: \( f'(x) = 3x^2 - 2 \)
Valutiamo la derivata in \( x_0 = 2 \):
Il differenziale nel punto \( x_0 = 2 \) è:
Esempio 3: Differenziale con punto e incremento dati
Calcolare il differenziale della funzione \( f(x) = \sqrt{x} \) nel punto \( x_0 = 4 \) con incremento \( \Delta x = 0.1 \).
Calcoliamo la derivata: \( f'(x) = \frac{1}{2\sqrt{x}} \)
Valutiamo la derivata in \( x_0 = 4 \):
Il differenziale con \( dx = \Delta x = 0.1 \) è:
Interpretazione geometrica del risultato:
Il differenziale \( df = 0.025 \) rappresenta l'incremento lungo la retta tangente al grafico della funzione nel punto \( x_0 = 4 \).
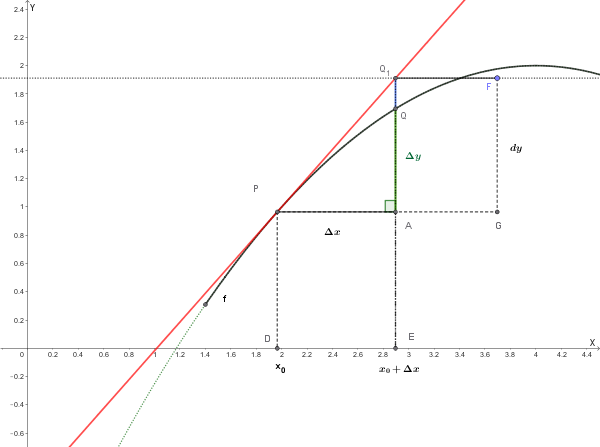
Come si vede dalla figura:
- Il differenziale \( dy \) (segmento verticale FG) rappresenta la variazione calcolata lungo la retta tangente quando \( x \) aumenta di \( \Delta x = 0.1 \)
- L'incremento reale \( \Delta y \) (segmento verticale QA) rappresenta la variazione effettiva lungo la curva della funzione
- La differenza tra i due (FG-QA), è l'errore di approssimazione (tanto più piccolo quanto più \( \Delta x \) è piccolo)
Confronto numerico:
- La variazione reale della funzione è: \( \Delta f = \Delta y =f(4.1) - f(4) = \sqrt{4.1} - \sqrt{4} = 2.0248... - 2 = 0.0248... \)
- La variazione approssimata tramite il differenziale è: \( df =dy= 0.025 \)
- L'errore è: \( |\Delta y - dy| \approx 0.0002 \), cioè solo lo 0.8%!
Il differenziale fornisce quindi una stima molto accurata della variazione reale. L'approssimazione è tanto più precisa quanto più piccolo è l'incremento \( \Delta x \).
Conclusione geometrica: Il differenziale rappresenta la variazione lungo la retta tangente al grafico della funzione, mentre \( \Delta f \) rappresenta la variazione lungo la curva effettiva. Sostituire \( \Delta f \) con \( df \) equivale geometricamente a sostituire la curva con la sua tangente nell'intorno del punto considerato.