

Versione accessibile con soluzioni dettagliate
🏗️ Integrazione Numerica
📚 Disponibile anche in versione standard
a) Metodi di integrazione numerica
L'integrazione numerica è un metodo per calcolare il valore approssimato di un integrale definito quando non è possibile o conveniente calcolare la primitiva in modo analitico.
Metodo dei Trapezi: l'intervallo \([a,b]\) viene suddiviso in \(n\) parti uguali di ampiezza \(h=\frac{b-a}{n}\). L'area sotto la curva viene approssimata con la somma delle aree di \(n\) trapezi. È generalmente più preciso del metodo dei rettangoli.
Metodo dei Rettangoli: l'intervallo viene suddiviso in \(n\) parti uguali. L'area viene approssimata con la somma delle aree di \(n\) rettangoli. Si distinguono rettangoli inscritti (approssimazione per difetto) e circoscritti (approssimazione per eccesso). Il valore approssimato si ottiene come media delle due somme.
Questo metodo permette di calcolare in modo approssimato \(\int_a^b f(x)\, dx\):
1. Suddivisione dell'intervallo \([a, b]\) in \(n\) parti uguali:
➔ \(h = \dfrac{b-a}{n}\) (ampiezza passo)
2. Calcolo delle aree dei trapezi:
▷ Area trapezio \(i\)-esimo: \(\dfrac{(f(x_i) + f(x_{i+1})) \cdot h}{2}\)
3. Formula composita: \[ T_n = \frac{h}{2} \left[ f(x_0) + 2\bigl(f(x_1) + f(x_2) + \cdots + f(x_{n-1})\bigr) + f(x_n) \right] \]
4. Errore: metodo più preciso di quello dei rettangoli.
Questo metodo permette di calcolare in modo approssimato \(\int_a^b f(x)\, dx\).
Due varianti principali (per funzione crescente):
① Rettangoli inscritti (somma inferiore): approssimazione per difetto
② Rettangoli circoscritti (somma superiore): approssimazione per eccesso
Procedimento:
1. Suddivisione in \(n\) intervalli: \(h = \dfrac{b-a}{n}\)
2. Scelta del punto campione:
- Inscritti: punto iniziale \(x_i\)
- Circoscritti: punto finale \(x_{i+1}\)
Formule: \[ R_i = h \cdot \sum_{i=0}^{n-1} f(x_i) \quad \text{(inscritti)} \] \[ R_c = h \cdot \sum_{i=1}^{n} f(x_i) \quad \text{(circoscritti)} \]
Due varianti principali (per funzione decrescente):
① Rettangoli inscritti (somma inferiore): approssimazione per difetto
② Rettangoli circoscritti (somma superiore): approssimazione per eccesso
Procedimento:
1. Suddivisione in \(n\) intervalli: \(h = \dfrac{b-a}{n}\)
2. Scelta del punto campione:
- Circoscritti: punto iniziale \(x_i\)
- Inscritti: punto finale \(x_{i+1}\)
Formule: \[ R_c = h \cdot \sum_{i=0}^{n-1} f(x_i) \quad \text{(circoscritti)} \] \[ R_i = h \cdot \sum_{i=1}^{n} f(x_i) \quad \text{(inscritti)} \]
Si prende come valore approssimato dell'integrale la media aritmetica: \[ \text{Media} = \frac{R_i + R_c}{2} \]
Errore: metodo meno preciso di quello dei trapezi.
b) Calcola il valore esatto dell'integrale \(\displaystyle\int_2^4 \frac{1}{x-1}\,dx\)
Rappresentiamo, come aiuto grafico, la funzione (che è un'iperbole equilatera traslata) insieme alla regione la cui area è data dall'integrale da calcolare.

Calcolo analitico: \[ \int_2^4 \frac{1}{x-1}\,dx = \Big[\ln|x-1|\Big]_2^4 = \ln(3) - \ln(1) = \ln(3) \approx 1.0986 \]
c) Calcola il valore approssimato dell'integrale \(\displaystyle\int_2^4 \frac{1}{x-1}\,dx\) con \(n=5\)
Mostriamo il grafico, anche se non è necessario per il calcolo richiesto.
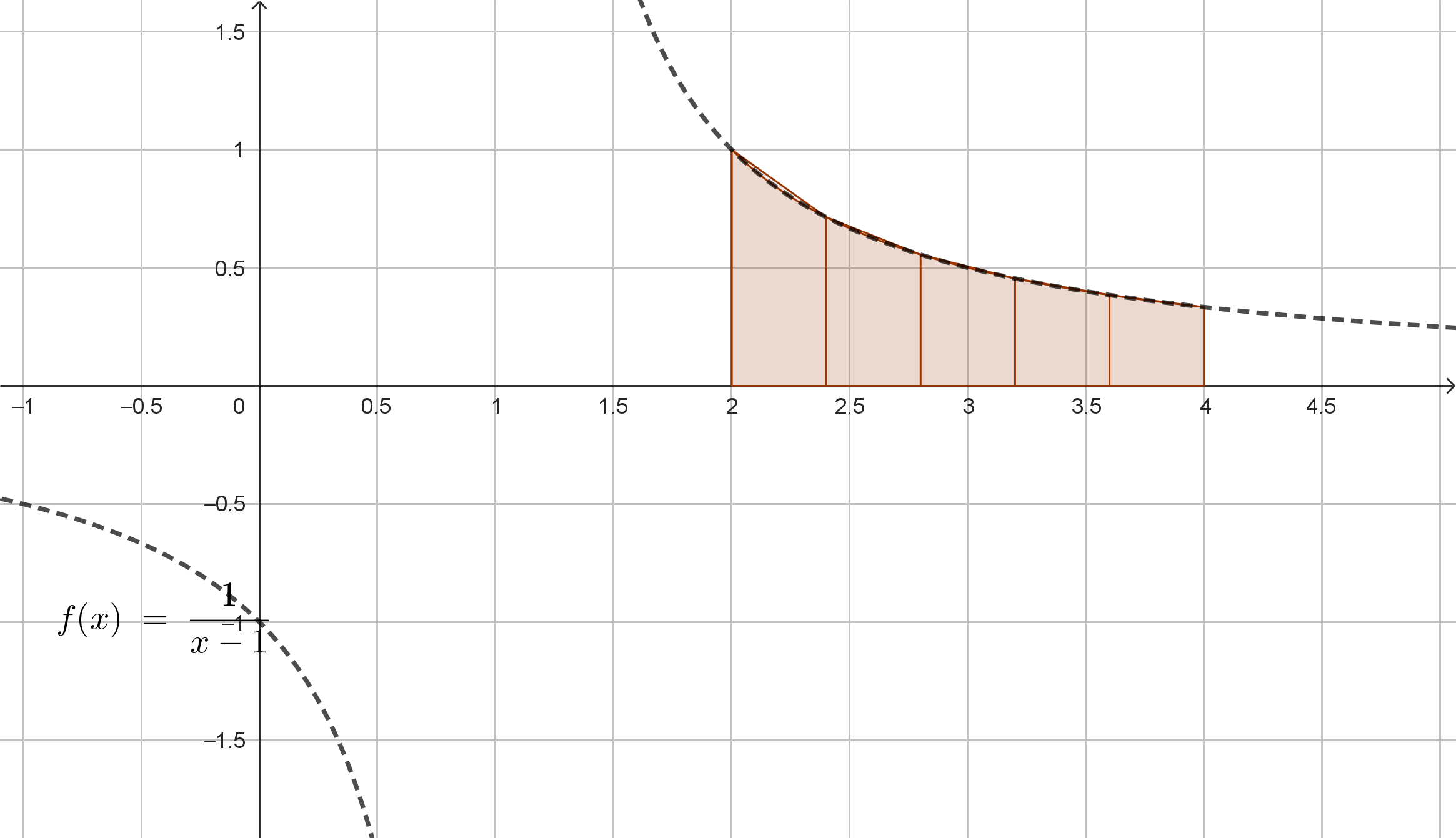
\(h = \dfrac{4-2}{5} = 0.4\)
\(x_0=2.0 \Rightarrow f(x_0)=1.0000\)
\(x_1=2.4 \Rightarrow f(x_1)=0.7143\)
\(x_2=2.8 \Rightarrow f(x_2)=0.5556\)
\(x_3=3.2 \Rightarrow f(x_3)=0.4545\)
\(x_4=3.6 \Rightarrow f(x_4)=0.3846\)
\(x_5=4.0 \Rightarrow f(x_5)=0.3333\)
\(h = 0.4\)
Rettangoli inscritti.
Mostriamo il grafico, anche se non è necessario per il calcolo richiesto.
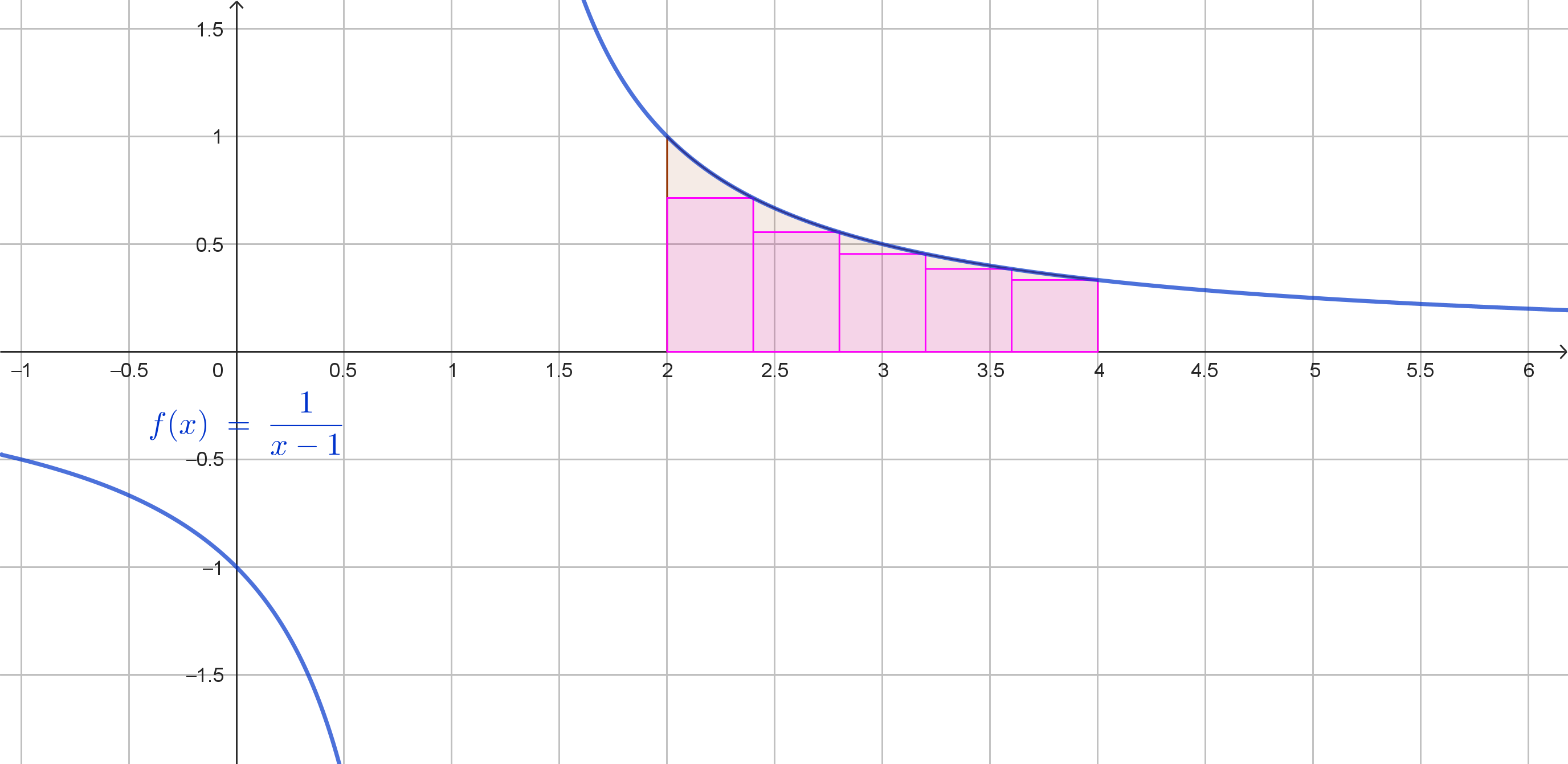
\(x_1=2.4 \Rightarrow f(x_1)=0.7143\)
\(x_2=2.8 \Rightarrow f(x_2)=0.5556\)
\(x_3=3.2 \Rightarrow f(x_3)=0.4545\)
\(x_4=3.6 \Rightarrow f(x_4)=0.3846\)
\(x_5=4.0 \Rightarrow f(x_5)=0.3333\)
Rettangoli circoscritti.
Mostriamo il grafico, anche se non è necessario per il calcolo richiesto.
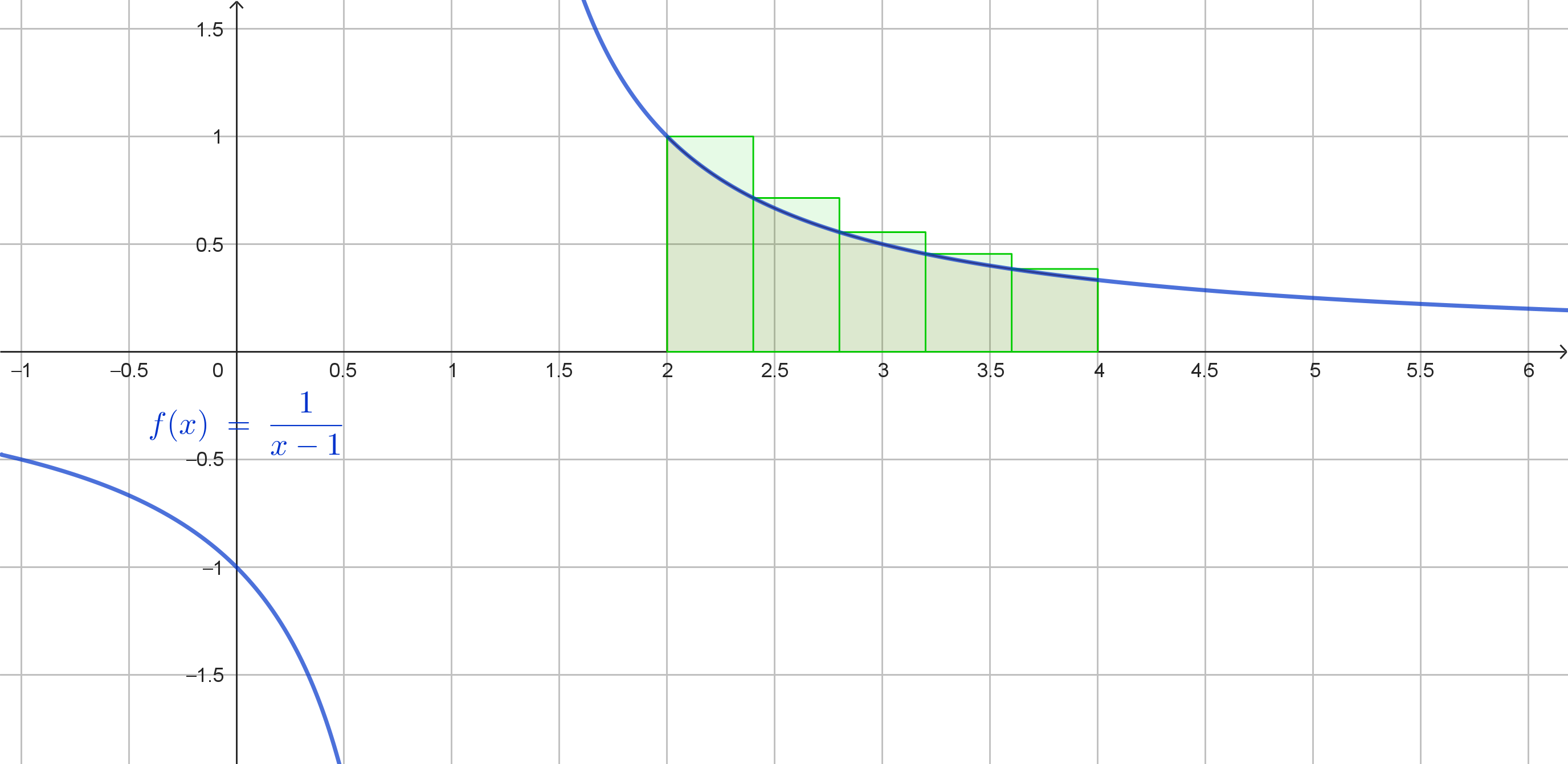
\(x_0=2.0 \Rightarrow f(x_0)=1.0000\)
\(x_1=2.4 \Rightarrow f(x_1)=0.7143\)
\(x_2=2.8 \Rightarrow f(x_2)=0.5556\)
\(x_3=3.2 \Rightarrow f(x_3)=0.4545\)
\(x_4=3.6 \Rightarrow f(x_4)=0.3846\)
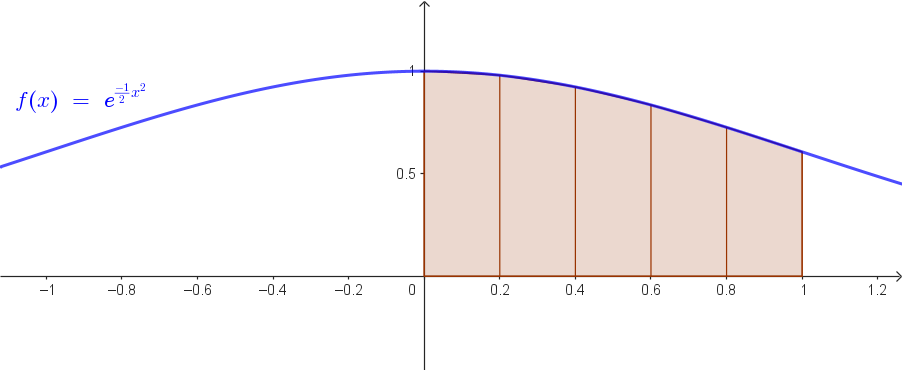
d) Calcola il valore approssimato dell'integrale \(\displaystyle\int_0^1 e^{-\frac{1}{2}x^2}\,dx\) con \(n=5\)
Consideriamo la funzione \(f(x) = e^{-\frac{x^2}{2}}\) e calcoliamo \(\displaystyle\int_0^1 f(x)\,dx\) con \(n=5\).
\(h = \dfrac{1-0}{5} = 0.2\)
\(x_0=0.0 \Rightarrow f(0.0) = 1.0000\)
\(x_1=0.2 \Rightarrow f(0.2) \approx 0.9802\)
\(x_2=0.4 \Rightarrow f(0.4) \approx 0.9231\)
\(x_3=0.6 \Rightarrow f(0.6) \approx 0.8353\)
\(x_4=0.8 \Rightarrow f(0.8) \approx 0.7261\)
\(x_5=1.0 \Rightarrow f(1.0) \approx 0.6065\)
Consideriamo la funzione \(f(x) = e^{-\frac{x^2}{2}}\) e calcoliamo \(\displaystyle\int_0^1 f(x)\,dx\) con \(n=5\).
\(h = 0.2\)
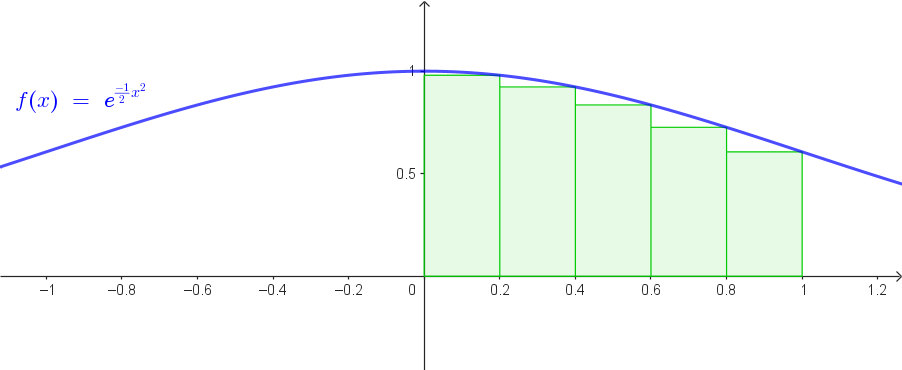
1. Rettangoli inscritti (la funzione è decrescente):
\(f(0.2)\approx 0.9802,\ f(0.4)\approx 0.9231,\ f(0.6)\approx 0.8353,\ f(0.8)\approx 0.7261,\ f(1.0)\approx 0.6065\)
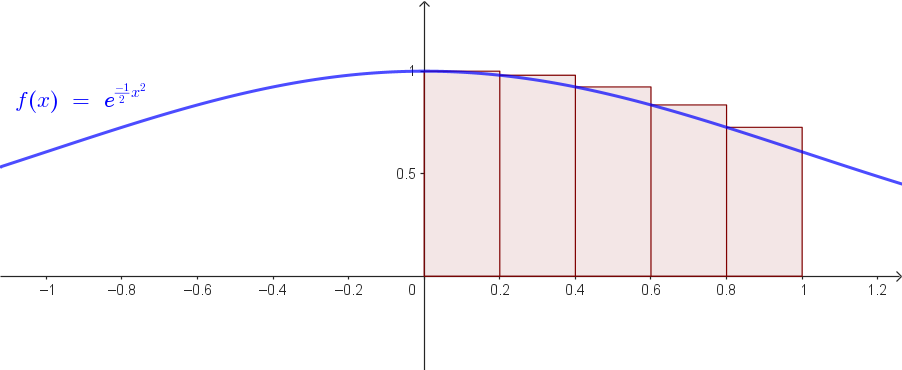
2. Rettangoli circoscritti:
\(f(0.0)=1.0000,\ f(0.2)\approx 0.9802,\ f(0.4)\approx 0.9231,\ f(0.6)\approx 0.8353,\ f(0.8)\approx 0.7261\)
e) Calcola il valore approssimato dell'integrale \(\displaystyle\int_{-2}^{-1} \frac{1}{x^2+4x+5}\,dx\) con \(n=5\)
Consideriamo \(f(x) = \dfrac{1}{x^2+4x+5}\) e calcoliamo \(\displaystyle\int_{-2}^{-1} f(x)\,dx\) con \(n=5\).
\(h = \dfrac{-1-(-2)}{5} = \dfrac{1}{5} = 0.2\)
\(x_0=-2.0 \Rightarrow f(-2.0) = 1.0000\)
\(x_1=-1.8 \Rightarrow f(-1.8) \approx 0.9615\)
\(x_2=-1.6 \Rightarrow f(-1.6) \approx 0.8621\)
\(x_3=-1.4 \Rightarrow f(-1.4) \approx 0.7353\)
\(x_4=-1.2 \Rightarrow f(-1.2) \approx 0.6098\)
\(x_5=-1.0 \Rightarrow f(-1.0) = 0.5000\)
Consideriamo \(f(x) = \dfrac{1}{x^2+4x+5}\) e calcoliamo \(\displaystyle\int_{-2}^{-1} f(x)\,dx\) con \(n=5\).
\(h = 0.2\)
1. Rettangoli inscritti.
\(f(-1.8)\approx 0.9615,\ f(-1.6)\approx 0.8621,\ f(-1.4)\approx 0.7353,\ f(-1.2)\approx 0.6098,\ f(-1.0)=0.5\)
\[ R_i = 0.2 \times 3.6687 \approx 0.7337 \]2. Rettangoli circoscritti.
\(f(-2.0)=1,\ f(-1.8)\approx 0.9615,\ f(-1.6)\approx 0.8621,\ f(-1.4)\approx 0.7353,\ f(-1.2)\approx 0.6098\)
\[ R_c = 0.2 \times 4.1687 \approx 0.8337 \] \[ \text{Media} = \frac{0.8337 + 0.7337}{2} \approx 0.784 \]f) Calcola: \(\displaystyle\int_0^1 \sqrt{\frac{1-x}{1+x}}\,dx\)
Mostriamo il grafico, anche se non richiesto:
![Grafico funzione √[(1-x)/(1+x)]](graphff.png)
1. Riscriviamo la funzione: \[ \sqrt{\frac{1-x}{1+x}} = \frac{1-x}{\sqrt{1-x^2}} \]
2. Separiamo l'integrale: \[ \int \frac{1}{\sqrt{1-x^2}}\,dx - \int \frac{x}{\sqrt{1-x^2}}\,dx \]
3. Calcoliamo le primitive: \[ = \arcsin(x) + \sqrt{1-x^2} + C \]
4. Valutiamo tra 0 e 1: \[ \Big[\arcsin(x) + \sqrt{1-x^2}\Big]_0^1 = \bigl[\arcsin(1) + 0\bigr] - \bigl[\arcsin(0) + 1\bigr] = \frac{\pi}{2} - 1 \approx 0.5708 \]
Mostriamo il grafico, anche se non richiesto:
![Grafico funzione √[(1-x)/(1+x)]](graphfftrapezi.png)
\(h = \dfrac{1-0}{5} = 0.2\)
\(x_0=0,\ x_1=0.2,\ x_2=0.4,\ x_3=0.6,\ x_4=0.8,\ x_5=1\)
Valori funzione:
\(f(0)=1,\ f(0.2)\approx 0.816,\ f(0.4)\approx 0.655,\ f(0.6)\approx 0.5,\ f(0.8)\approx 0.333,\ f(1)=0\)
1. Rettangoli inscritti.
Mostriamo il grafico, anche se non richiesto:
![Grafico funzione √[(1-x)/(1+x)]](graphffrettangoliinscritti.png)
\(h = \dfrac{1-0}{5} = 0.2\)
\(f(0)=1,\ f(0.2)\approx 0.816,\ f(0.4)\approx 0.655,\ f(0.6)\approx 0.5,\ f(0.8)\approx 0.333,\ f(1)=0\)
2. Rettangoli circoscritti.
![Grafico funzione √[(1-x)/(1+x)]](graphffrettangolicircoscritti.png) \[ R_c = 0.2 \times 3.304 \approx 0.6608 \]
\[ R_c = 0.2 \times 3.304 \approx 0.6608 \]
3. Media dei due metodi: \[ R = \frac{0.6608 + 0.4608}{2} \approx 0.5608 \approx 0.561 \]