

Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.


Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
Trovare una formula che permetta di calcolare il numero delle diagonali di un poligono convesso di \(n\) lati e dimostrarla per induzione.
Soluzione quesito 1:
Consideriamo un poligono convesso con \(n\) lati (e quindi \(n\) vertici).
Da ogni vertice di un poligono possiamo tracciare una linea verso tutti gli altri vertici. Ci sono \(n\) vertici in totale.
Se moltiplichiamo il numero di vertici (\(n\)) per il numero di diagonali che partono da ciascun vertice (\(n-3\)), otteniamo \(n(n-3)\).
Tuttavia, in questo modo abbiamo contato ogni diagonale due volte (una volta per ogni vertice che essa congiunge). Ad esempio, la diagonale da A a C viene contata quando partiamo da A e quando partiamo da C.
Quindi, dobbiamo dividere per 2. La formula per il numero di diagonali \(D_n\) di un poligono convesso con \(n\) lati è:
\[ D_n = \frac{n(n-3)}{2} \]Questa formula è valida per poligoni con \(n \ge 3\) lati, poiché un poligono ha almeno 3 lati. Un triangolo (n=3) ha 0 diagonali, e la formula dà \(\frac{3(3-3)}{2} = 0\), che è corretto.
Dimostreremo per induzione che la formula \(D_n = \frac{n(n-3)}{2}\) è vera per ogni \(n \ge 3\).
Per un poligono con \(n=3\) lati (un triangolo), sappiamo che il numero di diagonali è 0.
Usiamo la formula per \(n=3\):
\[ D_3 = \frac{3(3-3)}{2} = \frac{3 \cdot 0}{2} = 0 \]La formula è vera per \(n=3\).
Assumiamo che la formula sia vera per un generico poligono di \(n\) lati (ipotesi induttiva):
\[ D_n = \frac{n(n-3)}{2} \quad \text{(Ipotesi Induttiva)} \]Ora dobbiamo dimostrare che la formula è vera anche per un poligono di \(n+1\) lati, cioè che:
\[ D_{n+1} = \frac{(n+1)((n+1)-3)}{2} = \frac{(n+1)(n-2)}{2} \]Consideriamo un poligono convesso con \(n+1\) lati. Possiamo visualizzarlo partendo da un poligono di \(n\) lati e aggiungendo un nuovo vertice. Sia \(V_1, V_2, \dots, V_n\) i vertici di un poligono con \(n\) lati, e aggiungiamo un nuovo vertice \(V_{n+1}\) tra \(V_n\) e \(V_1\). Così facendo, il lato \(V_n V_1\) del poligono originale diventa una diagonale del nuovo poligono.
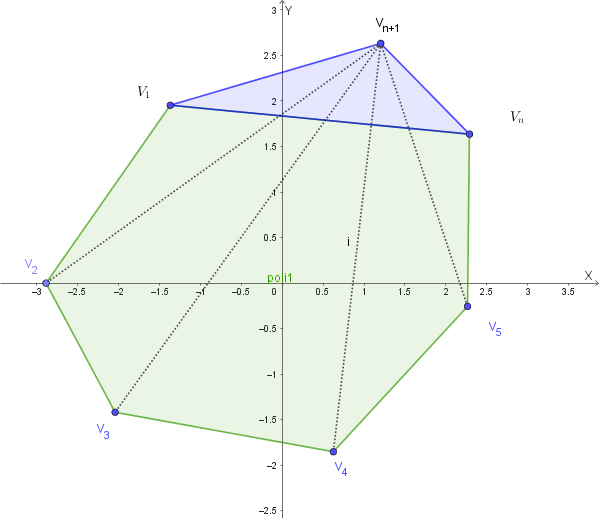
Quando passiamo da un poligono di \(n\) lati a uno di \(n+1\) lati:
Dunque, il numero di diagonali del poligono con \(n+1\) lati è dato dal numero di diagonali del poligono di \(n\) lati più le nuove diagonali aggiunte:
\[ D_{n+1} = D_n + (\text{numero di nuove diagonali}) \] \[ D_{n+1} = D_n + 1 + (n-2) \] \[ D_{n+1} = D_n + n-1 \]Per l'ipotesi induttiva, sappiamo che \(D_n = \frac{n(n-3)}{2}\). Sostituiamo:
\[ D_{n+1} = \frac{n(n-3)}{2} + (n-1) \]Ora, mettiamo a comune denominatore:
\[ D_{n+1} = \frac{n(n-3) + 2(n-1)}{2} \] \[ D_{n+1} = \frac{n^2 - 3n + 2n - 2}{2} \] \[ D_{n+1} = \frac{n^2 - n - 2}{2} \]Per completare la dimostrazione, dobbiamo mostrare che \(n^2 - n - 2\) è uguale a \((n+1)(n-2)\):
\[ (n+1)(n-2) = n^2 - 2n + n - 2 = n^2 - n - 2 \]Perfetto! Quindi, possiamo scrivere:
\[ D_{n+1} = \frac{(n+1)(n-2)}{2} \]Questo è esattamente il lato destro della formula per \(n+1\).
Abbiamo dimostrato che il passo base è vero e che, se la proprietà vale per \(n\), allora vale anche per \(n+1\). Per il Principio di Induzione Matematica, la formula \(D_n = \frac{n(n-3)}{2}\) è vera per ogni poligono convesso con \(n \ge 3\) lati.
Dimostrare per induzione che la somma dei primi \(n\) numeri dispari è uguale a \(n^2\):
\[ 1 + 3 + 5 + \dots + (2n-1) = n^2 \]per ogni \(n \in \mathbb{N}, n \ge 1\).
Soluzione quesito 2:
Sostituiamo \(n=1\) nella formula. Il primo numero dispari è 1. Il lato destro è \(1^2 = 1\).
\[ 1 = 1^2 \]La formula è vera per \(n=1\).
Assumiamo che la formula sia vera per un generico \(n \ge 1\) (ipotesi induttiva):
\[ 1 + 3 + 5 + \dots + (2n-1) = n^2 \quad \text{(Ipotesi Induttiva)} \]Ora dobbiamo dimostrare che la formula è vera anche per \(n+1\), cioè che:
\[ 1 + 3 + 5 + \dots + (2n-1) + (2(n+1)-1) = (n+1)^2 \]Semplificando il termine \((2(n+1)-1)\):
\[ 2(n+1)-1 = 2n + 2 - 1 = 2n + 1 \]Quindi, dobbiamo dimostrare che:
\[ 1 + 3 + 5 + \dots + (2n-1) + (2n+1) = (n+1)^2 \]Partiamo dal lato sinistro dell'equazione per \(n+1\):
\[ (1 + 3 + 5 + \dots + (2n-1)) + (2n+1) \]Per l'ipotesi induttiva, sappiamo che \(1 + 3 + 5 + \dots + (2n-1)\) è uguale a \(n^2\). Sostituiamo:
\[ n^2 + (2n+1) \]Questa espressione è un quadrato perfetto:
\[ n^2 + 2n + 1 = (n+1)^2 \]Questo è esattamente il lato destro della formula per \(n+1\).
Abbiamo dimostrato che il passo base è vero e che, se la proprietà vale per \(n\), allora vale anche per \(n+1\). Per il principio di induzione matematica, la formula è vera per ogni \(n \in \mathbb{N}, n \ge 1\).
Dimostrare per induzione che la somma dei quadrati dei primi \(n\) numeri naturali è data dalla formula:
\[ 1^2 + 2^2 + 3^2 + \dots + n^2 = \frac{n(n+1)(2n+1)}{6} \]per ogni \(n \in \mathbb{N}, n \ge 1\).
Soluzione quesito 3:
Sostituiamo \(n=1\) nella formula:
\[ 1^2 = \frac{1(1+1)(2 \cdot 1+1)}{6} = \frac{1 \cdot 2 \cdot 3}{6} = \frac{6}{6} = 1 \]La formula è vera per \(n=1\).
Assumiamo che la formula sia vera per un generico \(n \ge 1\) (ipotesi induttiva):
\[ 1^2 + 2^2 + \dots + n^2 = \frac{n(n+1)(2n+1)}{6} \quad \text{(Ipotesi Induttiva)} \]Ora dobbiamo dimostrare che la formula è vera anche per \(n+1\), cioè che:
\[ 1^2 + 2^2 + \dots + n^2 + (n+1)^2 = \frac{(n+1)((n+1)+1)(2(n+1)+1)}{6} = \frac{(n+1)(n+2)(2n+3)}{6} \]Partiamo dal lato sinistro dell'equazione per \(n+1\):
\[ (1^2 + 2^2 + \dots + n^2) + (n+1)^2 \]Per l'ipotesi induttiva, sappiamo che \(1^2 + 2^2 + \dots + n^2\) è uguale a \(\frac{n(n+1)(2n+1)}{6}\). Sostituiamo:
\[ \frac{n(n+1)(2n+1)}{6} + (n+1)^2 \]Mettiamo in evidenza il termine \((n+1)\):
\[ (n+1) \left( \frac{n(2n+1)}{6} + (n+1) \right) \]Portiamo tutto a comune denominatore all'interno della parentesi:
\[ (n+1) \left( \frac{n(2n+1) + 6(n+1)}{6} \right) \] \[ (n+1) \left( \frac{2n^2 + n + 6n + 6}{6} \right) \] \[ (n+1) \left( \frac{2n^2 + 7n + 6}{6} \right) \]Ora dobbiamo fattorizzare il trinomio \(2n^2 + 7n + 6\). Possiamo trovare le radici risolvendo l'equazione \(2n^2 + 7n + 6 = 0\). Il discriminante è \(\Delta = 7^2 - 4 \cdot 2 \cdot 6 = 49 - 48 = 1\).
Le radici sono \(n = \frac{-7 \pm \sqrt{1}}{2 \cdot 2} = \frac{-7 \pm 1}{4}\). Quindi \(n_1 = \frac{-8}{4} = -2\) e \(n_2 = \frac{-6}{4} = -\frac{3}{2}\).
Pertanto, \(2n^2 + 7n + 6 = 2(n - (-2))(n - (-\frac{3}{2})) = 2(n+2)(n+\frac{3}{2}) = (n+2)(2n+3)\).
Sostituiamo questo nella nostra espressione:
\[ (n+1) \frac{(n+2)(2n+3)}{6} = \frac{(n+1)(n+2)(2n+3)}{6} \]Questo è esattamente il lato destro della formula per \(n+1\).
Abbiamo dimostrato che il passo base è vero e che, se la proprietà vale per \(n\), allora vale anche per \(n+1\). Per il principio di induzione matematica, la formula è vera per ogni \(n \in \mathbb{N}, n \ge 1\).
Dimostrare per induzione che \(n^3 - n\) è divisibile per 3 per ogni \(n \in \mathbb{N}, n \ge 1\).
Soluzione quesito 4:
Vogliamo dimostrare che \(n^3 - n\) è divisibile per 3 per ogni \(n \in \mathbb{N}, n \ge 1\). Questo significa che \(n^3 - n = 3m\) per qualche intero \(m\).
Sostituiamo \(n=1\) nell'espressione:
\[ 1^3 - 1 = 1 - 1 = 0 \]Poiché 0 è divisibile per 3 (\(0 = 3 \cdot 0\)), il passo base è verificato.
Assumiamo che la proprietà sia vera per un generico \(n \ge 1\) (ipotesi induttiva):
\[ n^3 - n \text{ è divisibile per 3} \quad \text{o equivalentemente, } n^3 - n = 3m \text{ per qualche intero } m \text{ (Ipotesi Induttiva)} \]Ora dobbiamo dimostrare che la proprietà è vera anche per \(n+1\), cioè che \((n+1)^3 - (n+1)\) è divisibile per 3.
Consideriamo l'espressione per \(n+1\):
\[ (n+1)^3 - (n+1) \]Espandiamo il cubo:
\[ (n^3 + 3n^2 + 3n + 1) - (n+1) \]Raggruppiamo i termini e semplifichiamo:
\[ n^3 + 3n^2 + 3n + 1 - n - 1 \] \[ (n^3 - n) + 3n^2 + 3n \]Ora, per l'ipotesi induttiva, sappiamo che \((n^3 - n)\) è divisibile per 3. Inoltre, \(3n^2\) è divisibile per 3 e \(3n\) è divisibile per 3.
Quindi, abbiamo la somma di tre termini, ognuno dei quali è divisibile per 3:
\[ (n^3 - n) + 3n^2 + 3n = 3m + 3n^2 + 3n = 3(m + n^2 + n) \]Dato che \((m + n^2 + n)\) è un intero, l'intera espressione \(3(m + n^2 + n)\) è divisibile per 3.
Abbiamo dimostrato che il passo base è vero e che, se la proprietà vale per \(n\), allora vale anche per \(n+1\). Per il principio di induzione matematica, \(n^3 - n\) è divisibile per 3 per ogni \(n \in \mathbb{N}, n \ge 1\).
Dimostrare per induzione che per ogni \(n \in \mathbb{N}, n \ge 1\), si ha:
\[ \sum_{i=1}^{n} \frac{1}{i(i+1)} = \frac{n}{n+1} \]Si dimostri la proprietà anche senza usare il Principio di induzione.
Soluzione quesito 5:
Sostituiamo \(n=1\) nella formula. Il lato sinistro è \(\frac{1}{1(1+1)} = \frac{1}{2}\). Il lato destro è \(\frac{1}{1+1} = \frac{1}{2}\).
\[ \frac{1}{2} = \frac{1}{2} \]La formula è vera per \(n=1\).
Assumiamo che la formula sia vera per un generico \(n \ge 1\) (ipotesi induttiva):
\[ \sum_{i=1}^{n} \frac{1}{i(i+1)} = \frac{n}{n+1} \quad \text{(Ipotesi Induttiva)} \]Ora dobbiamo dimostrare che la formula è vera anche per \(n+1\), cioè che:
\[ \sum_{i=1}^{n+1} \frac{1}{i(i+1)} = \frac{(n+1)}{((n+1)+1)} = \frac{n+1}{n+2} \]Partiamo dal lato sinistro dell'equazione per \(n+1\):
\[ \sum_{i=1}^{n+1} \frac{1}{i(i+1)} = \left( \sum_{i=1}^{n} \frac{1}{i(i+1)} \right) + \frac{1}{(n+1)((n+1)+1)} \] \[ = \left( \sum_{i=1}^{n} \frac{1}{i(i+1)} \right) + \frac{1}{(n+1)(n+2)} \]Per l'ipotesi induttiva, sappiamo che \(\sum_{i=1}^{n} \frac{1}{i(i+1)}\) è uguale a \(\frac{n}{n+1}\). Sostituiamo:
\[ \frac{n}{n+1} + \frac{1}{(n+1)(n+2)} \]Ora dobbiamo sommare queste due frazioni. Mettiamo a comune denominatore \((n+1)(n+2)\):
\[ \frac{n(n+2)}{(n+1)(n+2)} + \frac{1}{(n+1)(n+2)} \] \[ = \frac{n(n+2) + 1}{(n+1)(n+2)} \] \[ = \frac{n^2 + 2n + 1}{(n+1)(n+2)} \]Il numeratore \(n^2 + 2n + 1\) è un quadrato perfetto, \((n+1)^2\).
\[ = \frac{(n+1)^2}{(n+1)(n+2)} \]Possiamo semplificare un termine \((n+1)\) dal numeratore e dal denominatore (poiché \(n \ge 1\), \(n+1 \ne 0\)):
\[ = \frac{n+1}{n+2} \]Questo è esattamente il lato destro della formula per \(n+1\).
Abbiamo dimostrato che il passo base è vero e che, se la proprietà vale per \(n\), allora vale anche per \(n+1\). Per il principio di induzione matematica, la formula è vera per ogni \(n \in \mathbb{N}, n \ge 1\).
---La somma può essere dimostrata anche senza l'uso del principio di induzione, sfruttando il concetto di scomposizione in frazioni parziali.
Possiamo riscrivere il termine generico della somma \(\frac{1}{i(i+1)}\) come somma di due frazioni:
\(\frac{1}{i(i+1)}\) può essere scritto nella forma \(\frac{A}{i} + \frac{B}{i+1}\).
Per trovare i valori di \(A\) e \(B\), mettiamo a comune denominatore il lato destro:
\[ \frac{A}{i} + \frac{B}{i+1} = \frac{A(i+1) + Bi}{i(i+1)} = \frac{Ai + A + Bi}{i(i+1)} = \frac{(A+B)i + A}{i(i+1)} \]Ora, confrontiamo il numeratore con il numeratore della frazione originale, che è \(1\). Questo significa che il coefficiente di \(i\) deve essere 0 e il termine costante deve essere 1:
\[ \begin{cases} A+B = 0 \\ A = 1 \end{cases} \]Sostituendo \(A=1\) nella prima equazione, otteniamo \(1+B=0\), quindi \(B=-1\).
Perciò, la scomposizione in fratti semplici è:
\[ \frac{1}{i(i+1)} = \frac{1}{i} - \frac{1}{i+1} \]Ora, applichiamo questa scomposizione alla somma:
\[ \sum_{i=1}^{n} \frac{1}{i(i+1)} = \sum_{i=1}^{n} \left( \frac{1}{i} - \frac{1}{i+1} \right) \]Questa è una **somma telescopica**: la maggior parte dei termini si annullano a vicenda.
Scriviamo i primi termini e gli ultimi termini per capire meglio:
\[ \left( \frac{1}{1} - \frac{1}{2} \right) + \left( \frac{1}{2} - \frac{1}{3} \right) + \left( \frac{1}{3} - \frac{1}{4} \right) + \dots + \left( \frac{1}{n} - \frac{1}{n+1} \right) \]Come puoi vedere, il \(-1/2\) del primo termine si annulla con il \(+1/2\) del secondo, il \(-1/3\) del secondo si annulla con il \(+1/3\) del terzo, e così via.
Alla fine, rimangono solo il primo termine della prima parentesi e l'ultimo termine dell'ultima parentesi:
\[ = \frac{1}{1} - \frac{1}{n+1} \] \[ = 1 - \frac{1}{n+1} \]Mettendo a comune denominatore:
\[ = \frac{n+1 - 1}{n+1} \] \[ = \frac{n}{n+1} \]La formula è dimostrata senza l'uso dell'induzione.
Dimostrare per induzione che \(2^n > n\) per ogni \(n \in \mathbb{N}, n \ge 1\).
Soluzione quesito 6:
Sostituiamo \(n=1\) nella disuguaglianza:
\[ 2^1 > 1 \Rightarrow 2 > 1 \]La disuguaglianza è vera per \(n=1\).
Assumiamo che la disuguaglianza sia vera per un generico \(n \ge 1\) (ipotesi induttiva):
\[ 2^n > n \quad \text{(Ipotesi Induttiva)} \]Ora dobbiamo dimostrare che la disuguaglianza è vera anche per \(n+1\), cioè che:
\[ 2^{n+1} > n+1 \]Partiamo dal lato sinistro dell'espressione per \(n+1\):
\[ 2^{n+1} = 2 \cdot 2^n \]Per l'ipotesi induttiva, sappiamo che \(2^n > n\). Moltiplichiamo entrambi i lati di questa disuguaglianza per 2:
\[ 2 \cdot 2^n > 2 \cdot n \] \[ 2^{n+1} > 2n \]Ora, vogliamo dimostrare che \(2^{n+1} > n+1\). Se riusciamo a dimostrare che \(2n \ge n+1\) per \(n \ge 1\), allora per transitività avremo \(2^{n+1} > 2n \ge n+1\), il che implica \(2^{n+1} > n+1\).
Consideriamo la disuguaglianza \(2n \ge n+1\). Sottraiamo \(n\) da entrambi i lati:
\[ 2n - n \ge 1 \] \[ n \ge 1 \]Questa disuguaglianza è vera per tutti gli \(n \ge 1\), che è il nostro intervallo di validità.
Quindi, abbiamo \(2^{n+1} > 2n \ge n+1\). Questo implica \(2^{n+1} > n+1\).
Abbiamo dimostrato che il passo base è vero e che, se la proprietà vale per \(n\), allora vale anche per \(n+1\). Per il principio di induzione matematica, la disuguaglianza \(2^n > n\) è vera per ogni \(n \in \mathbb{N}, n \ge 1\).
Dimostrare per induzione che per ogni \(n \in \mathbb{N}, n \ge 1\), la somma delle prime \(n\) potenze di 2 (a partire da \(2^0\)) è data da: \[ 2^0 + 2^1 + 2^2 + \dots + 2^{n-1} = 2^n - 1 \]
Si dimostri la proprietà anche senza utilizzare il Principio di Induzione.
Soluzione quesito 7:
Sostituiamo \(n=1\) nella formula. Il lato sinistro ha solo il primo termine (per \(i=0\)), cioè \(2^0 = 1\). Il lato destro è \(2^1 - 1 = 2 - 1 = 1\).
\[ 1 = 1 \]La formula è vera per \(n=1\).
Assumiamo che la formula sia vera per un generico \(n \ge 1\) (ipotesi induttiva):
\[ 2^0 + 2^1 + \dots + 2^{n-1} = 2^n - 1 \quad \text{(Ipotesi Induttiva)} \]Ora dobbiamo dimostrare che la formula è vera anche per \(n+1\), cioè che:
\[ 2^0 + 2^1 + \dots + 2^{n-1} + 2^{((n+1)-1)} = 2^{n+1} - 1 \]Semplificando il termine \(2^{((n+1)-1)}\):
\[ 2^{((n+1)-1)} = 2^n \]Quindi, dobbiamo dimostrare che:
\[ 2^0 + 2^1 + \dots + 2^{n-1} + 2^n = 2^{n+1} - 1 \]Partiamo dal lato sinistro dell'equazione per \(n+1\):
\[ (2^0 + 2^1 + \dots + 2^{n-1}) + 2^n \]Per l'ipotesi induttiva, sappiamo che \(2^0 + 2^1 + \dots + 2^{n-1}\) è uguale a \(2^n - 1\). Sostituiamo:
\[ (2^n - 1) + 2^n \] \[ = 2 \cdot 2^n - 1 \] \[ = 2^{n+1} - 1 \]Questo è esattamente il lato destro della formula per \(n+1\).
Abbiamo dimostrato che il passo base è vero e che, se la proprietà vale per \(n\), allora vale anche per \(n+1\). Per il principio di induzione matematica, la formula è vera per ogni \(n \in \mathbb{N}, n \ge 1\).
---La nostra espressione, \(2^0 + 2^1 + 2^2 + \dots + 2^{n-1}\), rappresenta la somma dei primi \(n\) termini di una **progressione geometrica**. Il primo termine è \(a_0 = 2^0 = 1\) e la ragione è \(q=2\).
In generale, la somma \(S_n\) dei primi \(n\) termini di una progressione geometrica con primo termine \(a_0\) e ragione \(q\) è data dalla formula:
\[ S_n = a_0 + a_0 \cdot q + a_0 \cdot q^2 + \dots + a_0 \cdot q^{n-1} = a_0 \frac{1 - q^n}{1 - q} \]Nel nostro caso, abbiamo \(a_0 = 1\) e \(q=2\). Sostituendo questi valori nella formula, otteniamo:
\[ S_n = 1 \cdot \frac{1 - 2^n}{1 - 2} \] \[ S_n = \frac{1 - 2^n}{-1} \] \[ S_n = -(1 - 2^n) \] \[ S_n = 2^n - 1 \]Come si può vedere, la formula desiderata è ottenuta direttamente, senza l'uso del Principio di Induzione.
Dimostrare per induzione che per ogni \(n \in \mathbb{N}, n \ge 4\), si ha:
\[ n! > 2^n \]Soluzione quesito 8:
Sostituiamo \(n=4\) nella disuguaglianza:
\[ 4! > 2^4 \] \[ 4 \cdot 3 \cdot 2 \cdot 1 > 16 \] \[ 24 > 16 \]La disuguaglianza è vera per \(n=4\).
Assumiamo che la disuguaglianza sia vera per un generico \(n \ge 4\) (ipotesi induttiva):
\[ n! > 2^n \quad \text{(Ipotesi Induttiva)} \]Ora dobbiamo dimostrare che la disuguaglianza è vera anche per \(n+1\), cioè che:
\[ (n+1)! > 2^{n+1} \]Partiamo dal lato sinistro dell'espressione per \(n+1\):
\[ (n+1)! = (n+1) \cdot n! \]Per l'ipotesi induttiva, sappiamo che \(n! > 2^n\). Moltiplichiamo entrambi i lati di questa disuguaglianza per \((n+1)\):
\[ (n+1) \cdot n! > (n+1) \cdot 2^n \] \[ (n+1)! > (n+1) \cdot 2^n \]Ora, vogliamo dimostrare che \((n+1) \cdot 2^n \ge 2^{n+1}\). Se riusciamo a dimostrare questo, allora per transitività avremo \((n+1)! > (n+1) \cdot 2^n \ge 2^{n+1}\), il che implica \((n+1)! > 2^{n+1}\).
Consideriamo la disuguaglianza \((n+1) \cdot 2^n \ge 2^{n+1}\).
Possiamo riscrivere \(2^{n+1}\) come \(2 \cdot 2^n\). Quindi la disuguaglianza diventa:
\[ (n+1) \cdot 2^n \ge 2 \cdot 2^n \]Poiché \(2^n\) è sempre positivo, possiamo dividere entrambi i lati per \(2^n\) senza cambiare il verso della disuguaglianza:
\[ n+1 \ge 2 \]Questa disuguaglianza è vera per tutti gli \(n \ge 1\). Dato che la nostra base dell'induzione parte da \(n=4\), e \(4 \ge 1\), la condizione \(n+1 \ge 2\) è sicuramente soddisfatta.
Quindi, abbiamo \((n+1)! > (n+1) \cdot 2^n \ge 2^{n+1}\). Questo implica \((n+1)! > 2^{n+1}\).
Abbiamo dimostrato che il passo base è vero e che, se la proprietà vale per \(n\), allora vale anche per \(n+1\). Per il principio di induzione matematica, la disuguaglianza \(n! > 2^n\) è vera per ogni \(n \in \mathbb{N}, n \ge 4\).