

Risolvi da solo le 4 parti del Problema e controlla la soluzione premendo il tasto corrispondente.
1)
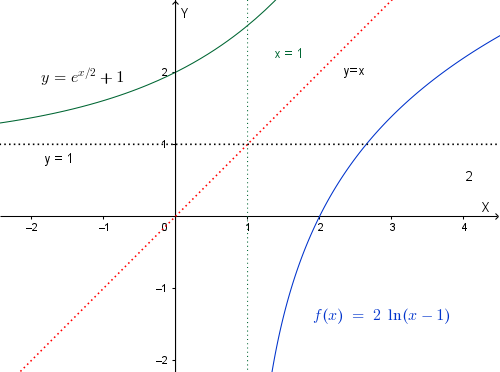
Nel piano riferito a coordinate cartesiane \(Oxy\), si disegni \(\Gamma\). Si scriva l'equazione della curva che è simmetrica di \(\Gamma\) rispetto all'asse \(y\) e si scrivano altresì le equazioni delle curve simmetriche di \(\Gamma\) rispetto alle rette \(x = 2\) e \(y = x\).
\(x=0\), non ha senso
\(y=0\), \(2 \ln (x -1) = 0 \implies x-1 = 1 \implies x = 1\)
\(f(x) \geq 0\) se \(x-1 \geq 1 \implies \quad x \geq 2\)
\(\lim_{x \to 1^+} 2 \ln(x-1) = -\infty\) (\(x=1\) asintoto verticale)
\(\lim_{x \to +\infty} 2 \ln(x-1) = +\infty\) (potrebbe esserci asintoto obliquo)
\(\lim_{x \to +\infty} \frac{2 \ln(x-1)}{x} = 0^+\) (non c'è asintoto obliquo)
\(y' = \frac{2}{x-1} > 0\) se \(x > 1\). Quindi nel dominio la funzione è sempre crescente: non ci sono minimi relativi né massimi relativi.
\(y'' = \frac{-2}{(x-1)^2} < 0 \quad \forall x\) del dominio: funzione sempre concava verso il basso, non ci sono flessi.
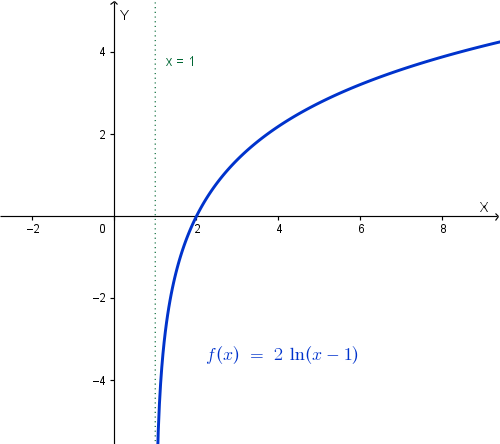
Il grafico di \(y = 2 \ln (x -1)\) si può ottenere a partire dal grafico di \(y = \ln (x)\) operando una traslazione verso destra di 1 ed una dilatazione verticale di fattore 2:
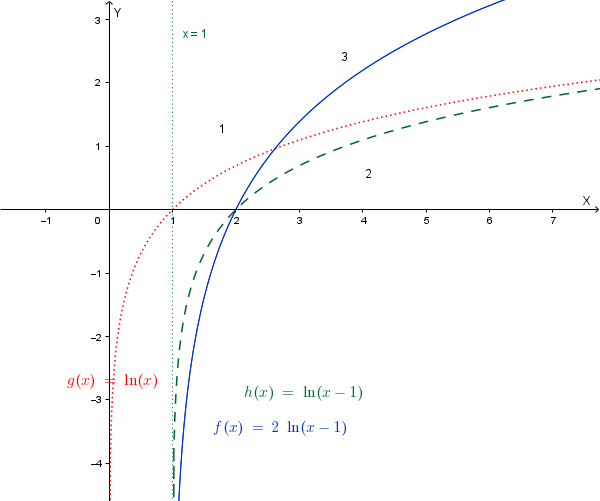
La simmetrica di \(\Gamma\) rispetto all'asse \(y\) si ottiene scambiando \(x\) in \(-x\):
\(y = 2 \ln (x -1) \implies y = 2\ln(-x-1)\)
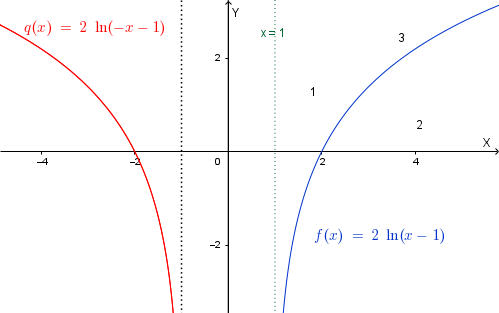
La simmetrica di \(\Gamma\) rispetto alla rette \(x=2\) si ottiene operando la seguente trasformazione:
\[ \begin{cases} x' = 4 - x \\ y' = y \end{cases} \implies \begin{cases} x \to 4 - x \\ y \to y \end{cases} \]\(y = 2 \ln (x -1) \implies y = 2 \ln(4 - x - 1) \implies y = 2\ln(3 - x)\)
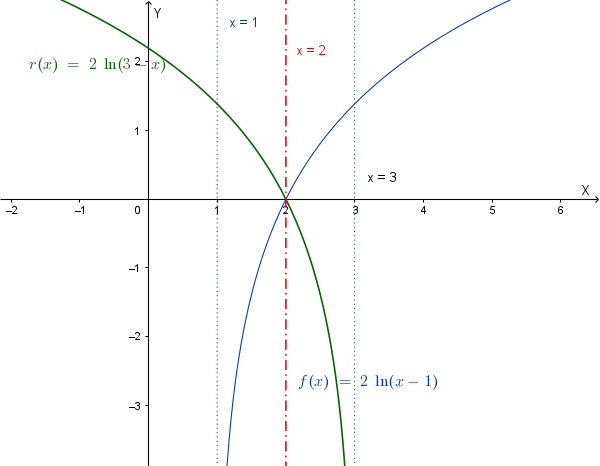
La simmetrica di \(\Gamma\) rispetto alla rette \(y=x\) si ottiene scambiando la \(x\) con la \(y\):
\(y = 2 \ln (x -1) \implies x = 2 \ln(y-1) \implies \frac{x}{2} = \ln(y-1) \implies y-1 = e^{x/2}\)
\(\implies y = e^{x/2} + 1\)
2)
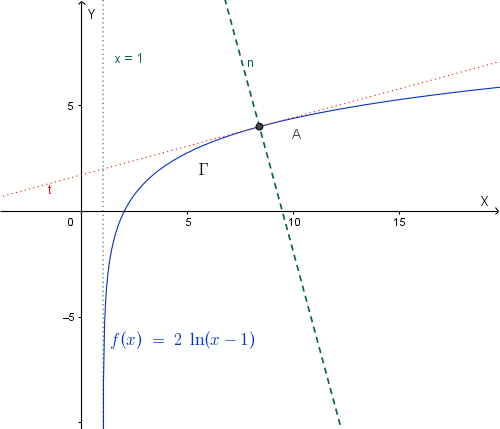
Si trovi l'equazione della normale a \(\Gamma\) nel suo punto di ascissa \(e^2+1\) dove \(e\) è il numero di Nepero.
\(y = 2 \ln (x -1) \implies y' = \frac{2}{x-1}\)
\(x = e^2 + 1 \implies y(e^2 + 1) = 2 \ln (e^2) = 4 \implies y'(e^2 + 1) = \frac{2}{e^2}\)
La normale \(n\) a \(\Gamma\) nel suo punto di ascissa \(e^2 + 1\) ha coefficiente angolare \(-\frac{e^2}{2}\), la sua equazione è quindi:
\(y - 4 = -\frac{e^2}{2} (x - e^2 - 1) \implies y = -\frac{e^2}{2} x + \frac{e^4}{2} + \frac{e^2}{2} + 4\)
3)
Si calcoli l'area della regione \(R\) del piano delimitata da \(\Gamma\), dall'asse \(x\) e dalla retta \(x = e^2 + 1\).
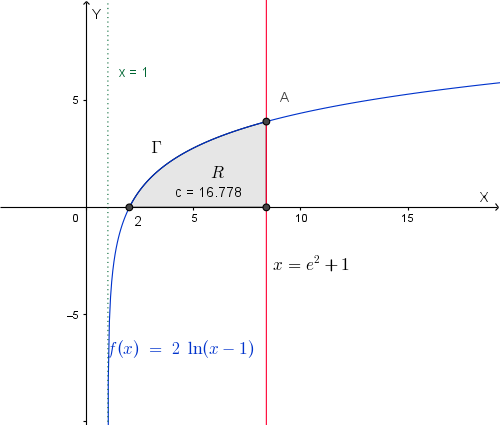
L'area della regione \(R\) si ottiene calcolando il seguente integrale:
\[ \text{Area}(R) = \int_{2}^{e^2 + 1} 2 \ln(x-1) \, dx \]Troviamo una primitiva di \(\ln (x -1)\) integrando per parti:
\[ \begin{align*} \int \ln(x-1) \, dx &= x\ln(x-1) - \int \frac{x}{x-1} \, dx \\ &= x\ln(x-1) - \int \frac{x-1+1}{x-1} \, dx \\ &= x\ln(x-1) - \int dx - \int \frac{1}{x-1} \, dx \\ &= x\ln(x-1) - x - \ln|x-1| + k \end{align*} \]Quindi:
\[ \begin{align*} \text{Area}(R) &= 2\left[x\ln(x-1) - x - \ln|x-1|\right]_{2}^{e^2 + 1} \\ &= 2\left[(e^2 + 1) \cdot 2 - e^2 - 1 - 2 - (-2)\right] \\ &= 2(e^2 + 1) \, \text{u}^2 \approx 16.78 \, \text{u}^2 \end{align*} \]4)
La regione \(R\) ruotando attorno all'asse \(y\) genera il solido \(\Omega\). Si calcoli il volume di \(\Omega\).
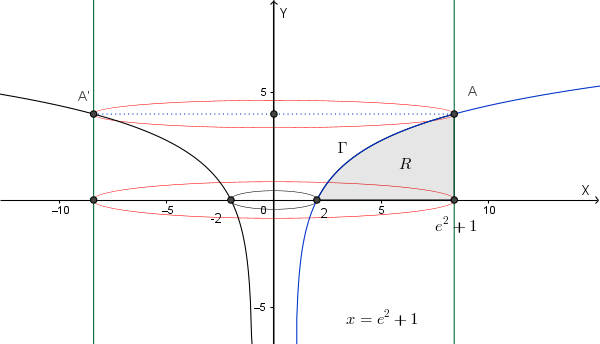
Il volume richiesto si può calcolare con il "metodo dei gusci cilindrici" mediante l'integrale:
\[ V(\Omega) = \int_{2}^{e^2 + 1} 2\pi x \cdot f(x) \, dx = 4\pi \int_{2}^{e^2 + 1} x \ln(x-1) \, dx \]Integrando per parti ponendo: \[ \begin{cases} u = \ln(x-1) \implies du = \frac{1}{x-1}dx \\ dv = x\,dx \implies v = \frac{x^2}{2} \end{cases} \]
Applichiamo la formula di integrazione per parti \(\int u\,dv = uv - \int v\,du\):
\[ \begin{align*} \int x \ln(x-1) \, dx &= \frac{x^2}{2}\ln(x-1) - \int \frac{x^2}{2(x-1)} dx \\ &= \frac{x^2}{2}\ln(x-1) - \frac{1}{2}\int \frac{x^2}{x-1} dx \end{align*} \]
Scomponiamo la frazione \(\frac{x^2}{x-1}\):
\[ \frac{x^2}{x-1} = x + 1 + \frac{1}{x-1} \]
Integriamo termine a termine:
\[ \begin{align*} \int \frac{x^2}{x-1} dx &= \int x\,dx + \int 1\,dx + \int \frac{1}{x-1}dx \\ &= \frac{x^2}{2} + x + \ln|x-1| \end{align*} \]
Sostituendo nell'espressione precedente:
\[ \begin{align*} \int x \ln(x-1) \, dx &= \frac{x^2}{2}\ln(x-1) - \frac{1}{2}\left(\frac{x^2}{2} + x + \ln|x-1|\right) + C \\ &= \frac{x^2}{2}\ln(x-1) - \frac{x^2}{4} - \frac{x}{2} - \frac{1}{2}\ln|x-1| + C \end{align*} \]
Riordinando i termini otteniamo il risultato finale:
\[ \int x \ln(x-1) \, dx = \frac{1}{2} x^2 \ln(x-1) - \frac{1}{4} x^2 - \frac{1}{2} x - \frac{1}{2} \ln|x-1| + C \]
Quindi:
\[ \begin{align*} 4\pi \int_{2}^{e^2 + 1} x \ln(x-1) \, dx &= 4\pi \left[-\frac{1}{4} x^2 + \frac{1}{2} x^2 \ln(x-1) - \frac{1}{2} x - \frac{1}{2} \ln(x-1)\right]_{2}^{e^2 + 1} \\ &= \pi(3e^4 + 4e^2 + 5) \, \text{u}^3 \approx 623.137 \, \text{u}^3 = V(\Omega) \end{align*} \]Per un ulteriore approfondimento sul Metodo dei gusci cilindrici si veda la seguente pagina di Matefilia:
http://www.matefilia.it/argomen/gusci-cilindrici/metodo-gusci-cilindrici.pdf
Il volume richiesto si può calcolare anche come differenza tra il volume \(V_1\) del cilindro con raggio di base \(e^2 + 1\) e altezza 4 ed il volume \(V_2\) del solido ottenuto dalla rotazione attorno all'asse \(y\) della regione delimitata dell'arco di \(\Gamma\) che delimita \(R\), dall'asse \(y\) e dalla retta \(y=4\).
\[ V_1 = \pi R^2 h = \pi(e^2 + 1)^2 \cdot 4 = 4\pi(e^4 + 2e^2 + 1) \]Per calcolare \(V_2\) consideriamo la funzione inversa di \(y = 2 \ln(x-1)\), che è \(x = g(y) = e^{y/2} + 1\) e calcoliamo il seguente integrale:
\[ \begin{align*} V_2 &= \pi \int_{0}^{4} g^2(y) \, dy = \pi \int_{0}^{4} (e^{y/2} + 1)^2 \, dy \\ &= \pi \int_{0}^{4} (e^y + 2e^{y/2} + 1) \, dy \\ &= \pi \left[e^y + 4e^{y/2} + y\right]_{0}^{4} = \pi(e^4 + 4e^2 - 1) \end{align*} \]Quindi:
\[ V(\Omega) = V_1 - V_2 = 4\pi(e^4 + 2e^2 + 1) - \pi(e^4 + 4e^2 - 1) = \pi(3e^4 + 4e^2 + 5) \, \text{u}^3 \]che coincide con il valore trovato con il metodo dei gusci cilindrici.