

Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.


Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
Considera la funzione \( f(x) = x^3 - 3x + 1 \) nell'intervallo \([0, 2]\).
Soluzione quesito 1:
Il Teorema di Lagrange (o del valor medio) afferma che se una funzione \( f(x) \):
allora esiste almeno un punto \( c \in (a, b) \) tale che: \[ f'(c) = \frac{f(b) - f(a)}{b - a} \]
In altre parole, esiste almeno un punto in cui la tangente al grafico è parallela alla retta secante passante per gli estremi dell'intervallo.
Ipotesi 1 - Continuità:
La funzione \( f(x) = x^3 - 3x + 1 \) è un polinomio, quindi è continua su tutto \(\mathbb{R}\), e in particolare è continua nell'intervallo \([0, 2]\). ✓
Ipotesi 2 - Derivabilità:
Essendo un polinomio, \( f(x) \) è derivabile su tutto \(\mathbb{R}\), quindi è derivabile nell'intervallo aperto \((0, 2)\). ✓
Conclusione: Entrambe le ipotesi del Teorema di Lagrange sono soddisfatte, quindi esiste almeno un punto \( c \in (0, 2) \) che soddisfa la tesi del teorema.
Calcoliamo i valori della funzione agli estremi:
\[ f(0) = 0^3 - 3 \cdot 0 + 1 = 1 \] \[ f(2) = 2^3 - 3 \cdot 2 + 1 = 8 - 6 + 1 = 3 \]Il rapporto incrementale (coefficiente angolare della retta secante) è:
\[ \frac{f(2) - f(0)}{2 - 0} = \frac{3 - 1}{2} = \frac{2}{2} = 1 \]Calcoliamo la derivata della funzione:
\[ f'(x) = \frac{d}{dx}(x^3 - 3x + 1) = 3x^2 - 3 \]Risolviamo l'equazione \( f'(c) = 1 \):
\[ 3c^2 - 3 = 1 \] \[ 3c^2 = 4 \] \[ c^2 = \frac{4}{3} \] \[ c = \pm \sqrt{\frac{4}{3}} = \pm \frac{2}{\sqrt{3}} = \pm \frac{2\sqrt{3}}{3} \]Verifichiamo quale soluzione appartiene all'intervallo aperto \((0, 2)\):
Calcoliamo il valore numerico: \(\frac{2\sqrt{3}}{3} \approx \frac{2 \cdot 1.732}{3} \approx 1.155\)
Il Teorema di Lagrange garantisce l'esistenza di almeno un punto in cui la tangente al grafico è parallela alla retta secante che congiunge i punti \((0, f(0)) = (0, 1)\) e \((2, f(2)) = (2, 3)\).
La retta secante ha equazione: \[ y - 1 = 1 \cdot (x - 0) \quad \Rightarrow \quad y = x + 1 \]
Nel punto \( c = \frac{2\sqrt{3}}{3} \), la tangente ha coefficiente angolare \( f'(c) = 1 \), quindi è parallela alla secante.
Risultato finale:
Il punto che soddisfa la tesi del Teorema di Lagrange è: \[ c = \frac{2\sqrt{3}}{3} \approx 1.155 \]
Le coordinate complete del punto sul grafico sono: \[ \left(\frac{2\sqrt{3}}{3}, f\left(\frac{2\sqrt{3}}{3}\right)\right) \]
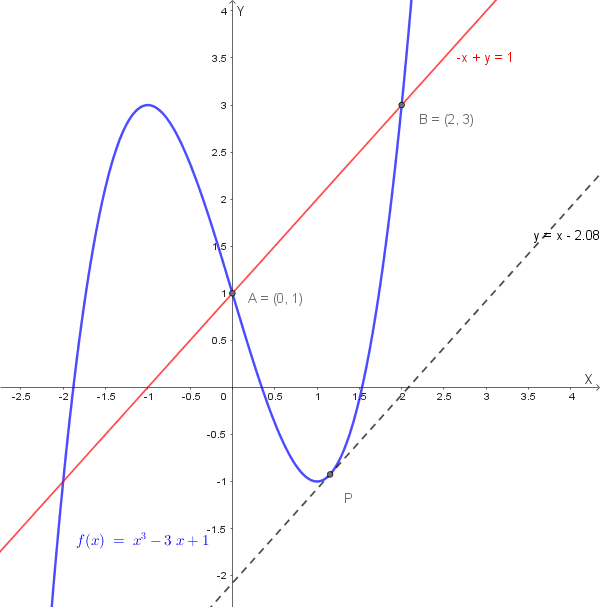
Il grafico mostra la funzione con la retta secante (in rosso) e il punto dove la tangente è parallela alla secante.
Dopo aver enunciato il Teorema del valor medio o di Lagrange, illustrane il legame con il teorema di Rolle e le implicazioni ai fini dello studio della monotonia di una funzione.
Soluzione quesito 2:
Il Teorema di Lagrange (o del valor medio) afferma:
Sia \(y = f(x)\) una funzione continua nell'intervallo chiuso e limitato \([a, b]\) e derivabile nell'intervallo aperto \((a, b)\). Esiste allora almeno un punto \(c\) nell'intervallo aperto tale che:
\[ \frac{f(b) - f(a)}{b - a} = f'(c) \]Il Teorema di Rolle è un corollario del Teorema di Lagrange.
Aggiungendo alle ipotesi del teorema di Lagrange l'ipotesi che sia \(f(a) = f(b)\), esso afferma che esiste almeno un punto \(c\) nell'intervallo aperto \((a, b)\) in cui si annulla la derivata prima.
Infatti, se \(f(a) = f(b)\), per il punto \(c\) di cui parla il teorema di Lagrange si ha:
\[ f'(c) = \frac{f(b) - f(a)}{b - a} = \frac{0}{b - a} = 0 \]In altre parole, il Teorema di Rolle è il caso particolare del Teorema di Lagrange quando i valori della funzione agli estremi coincidono.
Come corollario del teorema di Lagrange si ha il seguente teorema fondamentale, che permette di studiare la monotonia di una funzione:
Teorema sulla monotonia:
Nelle ipotesi del teorema di Lagrange, se la derivata della funzione nell'intervallo \((a, b)\)
è positiva allora la funzione è in esso crescente; se è negativa è decrescente.
Dimostriamo che se in \((a, b)\) la funzione ha derivata positiva allora è ivi crescente.
Tesi da dimostrare:
A tal fine occorre dimostrare che, scelti due punti qualsiasi \(x_1\) e \(x_2\) nell'intervallo, se \(x_1 < x_2\) allora \(f(x_1) < f(x_2)\).
Dimostrazione:
La funzione soddisfa le ipotesi del teorema di Lagrange nell'intervallo \([x_1, x_2]\), quindi esiste almeno un punto \(c\) tra \(x_1\) e \(x_2\) tale che:
\[ \frac{f(x_2) - f(x_1)}{x_2 - x_1} = f'(c) \]Ma per l'ipotesi sul segno della derivata risulta \(f'(c) > 0\), quindi, essendo il denominatore \(x_2 - x_1 > 0\) positivo, deve esserlo anche il numeratore, pertanto:
\[ f(x_2) - f(x_1) > 0 \quad \Rightarrow \quad f(x_2) > f(x_1) \]come si voleva dimostrare. ∎
Nota:
In modo del tutto analogo si dimostra il caso derivata negativa ⇒ funzione decrescente.
Questo teorema è di fondamentale importanza nell'analisi matematica perché:
| Condizione su \(f'(x)\) | Comportamento di \(f(x)\) |
|---|---|
| \(f'(x) > 0\) in \((a, b)\) | \(f(x)\) è crescente in \([a, b]\) |
| \(f'(x) < 0\) in \((a, b)\) | \(f(x)\) è decrescente in \([a, b]\) |
| \(f'(x) = 0\) in \((a, b)\) | \(f(x)\) è costante in \([a, b]\) |
Rappresenta il grafico della funzione:
\[ f(x) = \left|\frac{3 - 2x}{x - 3}\right| \]Verifica se negli intervalli \([0, 2]\) e \([4, 6]\) valgono le ipotesi del teorema di Lagrange, e in caso affermativo trova i punti la cui esistenza è prevista dal teorema di Lagrange.
Esiste un intervallo \([a, b]\) in cui si possa applicare il teorema di Rolle? Giustifica la risposta.
Soluzione quesito 3:
Il grafico di \(f\) si ottiene da quello di \(g(x) = \frac{3 - 2x}{x - 3}\) confermando la parte \(\geq 0\) e ribaltando la parte negativa rispetto all'asse \(x\).
La funzione \(g\) è una funzione omografica con:
I grafici di \(g\) ed \(f\) sono i seguenti:
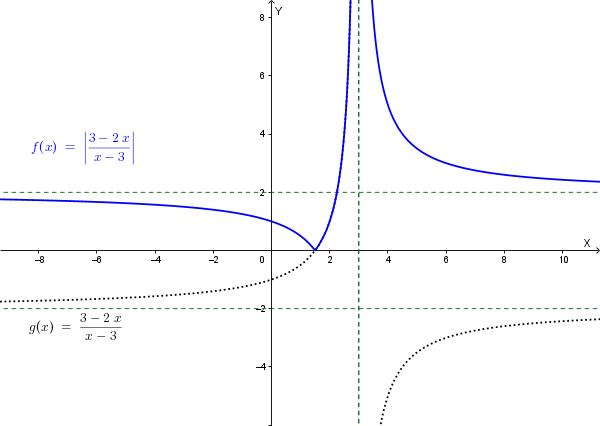
La funzione \(f\) è continua su tutto \(\mathbb{R}\), escluso \(x = 3\) (punto di discontinuità di seconda specie).
La funzione \(f\) è derivabile in tutti i punti del dominio, escluso \(x = \frac{3}{2}\), che, come si deduce dal grafico, è un punto angoloso.
Nell'intervallo \([0, 2]\) la funzione è continua ✓
Nell'intervallo \((0, 2)\) la funzione non è derivabile in \(x = \frac{3}{2}\) (punto angoloso) ✗
Conclusione: In tale intervallo NON vale il teorema di Lagrange.
Nell'intervallo \([4, 6]\) la funzione è continua ✓
Nell'intervallo \((4, 6)\) la funzione è derivabile ✓
Conclusione: In questo intervallo valgono le ipotesi del teorema di Lagrange.
Cerchiamo i punti \(c\) (interni all'intervallo \([4, 6]\)) per i quali:
\[ f'(c) = \frac{f(b) - f(a)}{b - a} \]Nell'intervallo \([4, 6]\), la funzione ha equazione \(f(x) = \frac{2x - 3}{x - 3}\) (la parte positiva dell'omografica).
Calcoliamo il rapporto incrementale:
\[ \frac{f(6) - f(4)}{6 - 4} = \frac{f(6) - f(4)}{2} \]Calcoliamo i valori:
\[ f(4) = \frac{2 \cdot 4 - 3}{4 - 3} = \frac{8 - 3}{1} = 5 \] \[ f(6) = \frac{2 \cdot 6 - 3}{6 - 3} = \frac{12 - 3}{3} = \frac{9}{3} = 3 \]Quindi:
\[ \frac{f(6) - f(4)}{2} = \frac{3 - 5}{2} = \frac{-2}{2} = -1 \]Calcoliamo la derivata della funzione:
\[ f'(x) = \frac{2(x - 3) - (2x - 3) \cdot 1}{(x - 3)^2} = \frac{2x - 6 - 2x + 3}{(x - 3)^2} = \frac{-3}{(x - 3)^2} \]Risolviamo l'equazione \(f'(c) = -1\):
\[ \frac{-3}{(c - 3)^2} = -1 \] \[ (c - 3)^2 = 3 \] \[ c - 3 = \pm\sqrt{3} \] \[ c = 3 \pm \sqrt{3} \]Le due soluzioni sono:
Risultato:
Il punto che soddisfa la tesi del teorema di Lagrange è: \[ c = 3 + \sqrt{3} \approx 4.73 \]
Non esiste alcun intervallo \([a, b]\) in cui si possa applicare il teorema di Rolle.
Giustificazione:
Infatti, oltre alla continuità nell'intervallo chiuso e alla derivabilità nell'aperto, dovrebbe verificarsi che \(f(a) = f(b)\).
Ma se osserviamo il grafico, una qualsiasi retta parallela all'asse \(x\) che incontri il grafico di \(f\) in due punti ha necessariamente all'interno:
Pertanto, le tre ipotesi del Teorema di Rolle (continuità, derivabilità e valori uguali agli estremi) non sono mai verificate contemporaneamente in nessun intervallo.
Data la funzione:
\[ f(x) = \begin{cases} x^3 & \text{se } 0 \leq x \leq 1 \\[10pt] x^2 - kx + k & \text{se } 1 < x \leq 2 \end{cases} \]Determina il parametro \(k\) in modo che nell'intervallo \([0, 2]\) sia applicabile il teorema di Lagrange e trova il punto di cui la tesi del teorema assicura l'esistenza.
Soluzione quesito 4:
Determiniamo \(k\) in modo che la funzione sia continua in \(x = 1\).
Si verifica facilmente che la funzione è continua per ogni \(k\), poiché il limite destro, il limite sinistro ed il valore che la funzione assume in 1 sono uguali (esattamente ad 1):
\[ \lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} x^3 = 1 \] \[ \lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} (x^2 - kx + k) = 1 - k + k = 1 \] \[ f(1) = 1^3 = 1 \]Quindi la continuità è garantita per ogni valore di \(k\). ✓
Dobbiamo imporre che la funzione sia derivabile in \(x = 1\).
Calcoliamo le derivate nei due rami:
Se \(0 \leq x < 1\): \(f'(x) = 3x^2\) e quindi: \[ \lim_{x \to 1^-} f'(x) = \lim_{x \to 1^-} 3x^2 = 3 \]
Se \(1 < x \leq 2\): \(f'(x) = 2x - k\) e quindi: \[ \lim_{x \to 1^+} f'(x) = \lim_{x \to 1^+} (2x - k) = 2 - k \]
Per la derivabilità in \(x = 1\) dovrà essere:
\[ 2 - k = 3 \quad \Rightarrow \quad k = -1 \]Funzione risultante:
\[ f(x) = \begin{cases} x^3 & \text{se } 0 \leq x \leq 1 \\[10pt] x^2 + x - 1 & \text{se } 1 < x \leq 2 \end{cases} \]Per tale valore di \(k = -1\) la funzione è:
Quindi sono soddisfatte le ipotesi del teorema di Lagrange. Pertanto esiste almeno un punto \(c\) interno all'intervallo tale che:
\[ \frac{f(b) - f(a)}{b - a} = f'(c) \]Calcoliamo il rapporto incrementale:
\[ \frac{f(2) - f(0)}{2 - 0} = f'(c) \]Calcoliamo i valori agli estremi:
\[ f(0) = 0^3 = 0 \] \[ f(2) = 2^2 + 2 - 1 = 4 + 2 - 1 = 5 \]Quindi:
\[ f'(c) = \frac{5 - 0}{2} = \frac{5}{2} \]Osserviamo che se \(x = 1\) la derivata della funzione vale 3, quindi \(c\) non può essere 1.
Caso 1: Se \(0 \leq x < 1\):
\[ 3x^2 = \frac{5}{2} \] \[ x^2 = \frac{5}{6} \] \[ x = \pm\sqrt{\frac{5}{6}} \]Poiché dobbiamo avere \(0 \leq x < 1\), accettiamo solo la soluzione positiva: \[ c = \sqrt{\frac{5}{6}} = \frac{\sqrt{30}}{6} \approx 0.913 \]
Caso 2: Se \(1 < x \leq 2\):
\[ 2x + 1 = \frac{5}{2} \] \[ 2x = \frac{3}{2} \] \[ x = \frac{3}{4} \]Questa soluzione è non accettabile perché \(\frac{3}{4} < 1\), quindi non appartiene all'intervallo \((1, 2]\).
Risultato finale:
Il parametro cercato è \(k = -1\) e il punto di cui la tesi del teorema assicura l'esistenza è:
\[ c = \sqrt{\frac{5}{6}} = \frac{\sqrt{30}}{6} \approx 0.913 \]In questo punto, la tangente al grafico della funzione è parallela alla retta secante che congiunge i punti \((0, 0)\) e \((2, 5)\).
Considerata la funzione \( f(x) = \sqrt{3 - 2x - x^2} \), stabilisci se sono verificate le ipotesi del teorema di Lagrange nell'intervallo \([-1, 1]\) e nel caso in cui siano verificate, determina le coordinate del punto che soddisfa il teorema.
Soluzione quesito 5:
La funzione è definita quando l'argomento della radice è non negativo:
\[ 3 - 2x - x^2 \geq 0 \] \[ -x^2 - 2x + 3 \geq 0 \] \[ x^2 + 2x - 3 \leq 0 \]Risolviamo l'equazione associata \(x^2 + 2x - 3 = 0\):
\[ x = \frac{-2 \pm \sqrt{4 + 12}}{2} = \frac{-2 \pm \sqrt{16}}{2} = \frac{-2 \pm 4}{2} \]Le soluzioni sono \(x_1 = -3\) e \(x_2 = 1\).
Quindi:
\[ x^2 + 2x - 3 \leq 0 \quad \text{per} \quad x \in [-3, 1] \]Dominio: \(D = [-3, 1]\)
L'intervallo \([-1, 1]\) è contenuto nel dominio \([-3, 1]\). ✓
Ipotesi 1 - Continuità in \([-1, 1]\):
La funzione è composizione di funzioni continue (radice quadrata e polinomio), quindi è continua nel suo dominio e in particolare in \([-1, 1]\). ✓
Ipotesi 2 - Derivabilità in \((-1, 1)\):
La funzione è derivabile in tutti i punti interni del dominio dove l'argomento della radice è strettamente positivo. Nell'intervallo \((-1, 1)\) risulta \(3 - 2x - x^2 > 0\), quindi la funzione è derivabile. ✓
Conclusione:
Sono verificate le ipotesi del teorema di Lagrange nell'intervallo \([-1, 1]\).
Calcoliamo i valori agli estremi:
\[ f(-1) = \sqrt{3 - 2(-1) - (-1)^2} = \sqrt{3 + 2 - 1} = \sqrt{4} = 2 \] \[ f(1) = \sqrt{3 - 2(1) - 1^2} = \sqrt{3 - 2 - 1} = \sqrt{0} = 0 \]Il rapporto incrementale è:
\[ \frac{f(1) - f(-1)}{1 - (-1)} = \frac{0 - 2}{2} = \frac{-2}{2} = -1 \]Calcoliamo la derivata di \(f(x) = \sqrt{3 - 2x - x^2}\):
\[ f'(x) = \frac{1}{2\sqrt{3 - 2x - x^2}} \cdot (-2 - 2x) = \frac{-2 - 2x}{2\sqrt{3 - 2x - x^2}} = \frac{-1 - x}{\sqrt{3 - 2x - x^2}} \]Dobbiamo risolvere l'equazione \(f'(c) = -1\):
\[ \frac{-1 - c}{\sqrt{3 - 2c - c^2}} = -1 \] \[ -1 - c = -\sqrt{3 - 2c - c^2} \] \[ 1 + c = \sqrt{3 - 2c - c^2} \]Eleviamo al quadrato entrambi i membri (con \(1 + c \geq 0\), cioè \(c \geq -1\)):
\[ (1 + c)^2 = 3 - 2c - c^2 \] \[ 1 + 2c + c^2 = 3 - 2c - c^2 \] \[ 2c^2 + 4c - 2 = 0 \] \[ c^2 + 2c - 1 = 0 \]Applicando la formula risolutiva:
\[ c = \frac{-2 \pm \sqrt{4 + 4}}{2} = \frac{-2 \pm \sqrt{8}}{2} = \frac{-2 \pm 2\sqrt{2}}{2} = -1 \pm \sqrt{2} \]Le soluzioni sono:
Calcoliamo \(f(c)\) con \(c = -1 + \sqrt{2}\):
\[ f(c) = \sqrt{3 - 2(-1 + \sqrt{2}) - (-1 + \sqrt{2})^2} \] \[ = \sqrt{3 + 2 - 2\sqrt{2} - (1 - 2\sqrt{2} + 2)} \] \[ = \sqrt{5 - 2\sqrt{2} - 3 + 2\sqrt{2}} \] \[ = \sqrt{2} \]Le coordinate del punto che soddisfa il teorema di Lagrange sono:
\[ \left(-1 + \sqrt{2}, \sqrt{2}\right) \approx (0.414, 1.414) \]In questo punto, la tangente al grafico della funzione è parallela alla retta secante che congiunge i punti \((-1, 2)\) e \((1, 0)\), entrambe con coefficiente angolare \(-1\).
La funzione \( f(x) = \sqrt{3 - 2x - x^2} \) può essere analizzata elevando al quadrato entrambi i membri (per \(y \geq 0\)):
\[ y = \sqrt{3 - 2x - x^2} \] \[ y^2 = 3 - 2x - x^2 \] \[ x^2 + y^2 + 2x - 3 = 0 \]Questa è l'equazione generale di una circonferenza. Per trovare centro e raggio, portiamo l'equazione nella forma canonica:
\[ x^2 + 2x + y^2 = 3 \] \[ x^2 + 2x + 1 + y^2 = 3 + 1 \] \[ (x + 1)^2 + y^2 = 4 \]Centro: \(C = (-1, 0)\) e raggio: \(r = 2\).
Poiché la funzione \(f(x)\) restituisce solo valori non negativi (essendo una radice quadrata), il grafico rappresenta la semicirconferenza superiore (con \(y \geq 0\)) della circonferenza completa.
Il dominio \([-3, 1]\) corrisponde esattamente al diametro orizzontale della circonferenza.
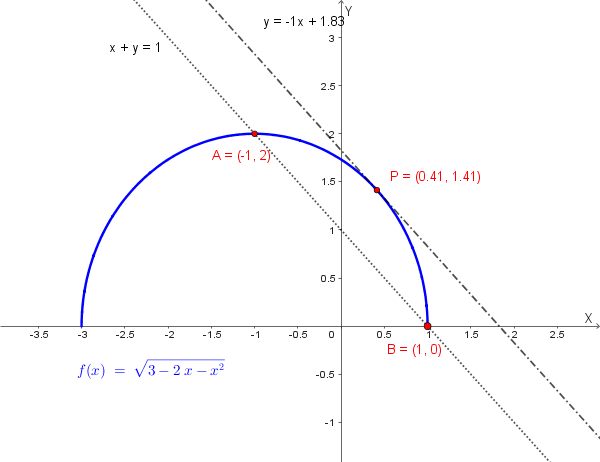
Il grafico mostra la semicirconferenza con la retta secante e il punto dove la tangente è parallela alla secante.
Utilizzando il Teorema di Lagrange, dimostra che, se la derivata di una funzione reale di variabile reale \(f(x)\) è nulla per ogni \(x\) di un dato intervallo \(J\), allora \(f(x)\) è costante in \(J\).
Soluzione quesito 6:
Ipotesi:
Supponiamo che \(f'(x) = 0\) per ogni \(x \in J\).
Tesi:
Dobbiamo dimostrare che \(f(x) = \text{costante}\) in \(J\).
Consideriamo un punto fisso \(a \in J\) e un generico punto \(x \in J\) con \(x > a\).
Consideriamo l'intervallo chiuso \([a, x]\) contenuto in \(J\). Essendo la funzione derivabile in \(J\), lo è anche in \([a, x]\); in tale intervallo la funzione è allora continua.
Per il Teorema di Lagrange applicato all'intervallo \([a, x]\), esiste almeno un punto \(c \in (a, x)\) tale che:
\[ \frac{f(x) - f(a)}{x - a} = f'(c) \]Ma per ipotesi \(f'(c) = 0\) (poiché \(c \in J\) e la derivata è nulla in tutto \(J\)), quindi:
\[ \frac{f(x) - f(a)}{x - a} = 0 \]Moltiplicando entrambi i membri per \((x - a) \neq 0\):
\[ f(x) - f(a) = 0 \] \[ f(x) = f(a) \]Poiché questo vale per ogni \(x \in J\), la funzione assume lo stesso valore \(f(a)\) in tutti i punti dell'intervallo \(J\).
Abbiamo dimostrato che \(f(x) = f(a)\) per ogni \(x \in J\), quindi la funzione è costante in \(J\). ∎
Questo teorema stabilisce che:
Se \(f(x) = 5\) in un intervallo \(J\), allora \(f'(x) = 0\) per ogni \(x \in J\).
Viceversa, se sappiamo che \(f'(x) = 0\) in un intervallo, possiamo concludere che \(f(x)\) deve essere una funzione costante in quell'intervallo.
Questo teorema vale per intervalli. Se la derivata è nulla solo in punti isolati (non in tutto un intervallo), la funzione non è necessariamente costante. Ad esempio, \(f(x) = x^3\) ha \(f'(0) = 0\), ma non è costante.
Dire, formalizzando la questione e utilizzando il teorema del valor medio o di Lagrange, se è vero che: «se un automobilista compie un viaggio senza soste in cui la velocità media è 60 km/h, allora almeno una volta durante il viaggio il tachimetro dell'automobile deve indicare esattamente 60 km/h».
Soluzione quesito 7:
Sia \(s = s(t)\) la legge oraria del moto, dove:
Il grafico dello spazio in funzione del tempo è del seguente tipo:
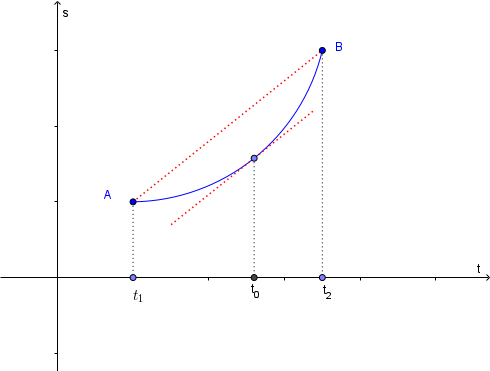
Il grafico mostra la funzione spazio-tempo con la retta secante AB il cui coefficiente angolare è pari alla velocità media.
La velocità media nell'intervallo di tempo \([t_1, t_2]\) è data da:
\[ v_m = \frac{s(t_2) - s(t_1)}{t_2 - t_1} = \text{coeff. ang. della retta } AB \]dove \(A = (t_1, s(t_1))\) e \(B = (t_2, s(t_2))\) sono i punti iniziale e finale del viaggio.
Per ipotesi, \(v_m = 60\) km/h.
La funzione \(s(t)\) (legge oraria) è:
Per il Teorema di Lagrange, esiste almeno un istante \(t_0 \in (t_1, t_2)\) tale che:
\[ s'(t_0) = \frac{s(t_2) - s(t_1)}{t_2 - t_1} = v_m = 60 \]Ma \(s'(t_0)\) è la velocità istantanea nell'istante \(t_0\), cioè la velocità indicata dal tachimetro nell'istante \(t_0\).
Quindi esiste almeno un istante \(t_0\) in cui la velocità dell'automobile è esattamente 60 km/h.
L'affermazione è VERA.
Se un automobilista compie un viaggio senza soste con velocità media di 60 km/h, il Teorema di Lagrange garantisce che almeno una volta durante il viaggio il tachimetro deve indicare esattamente 60 km/h.
Geometricamente, il teorema afferma che:
Se percorri 120 km in 2 ore, la tua velocità media è 60 km/h. Il Teorema di Lagrange garantisce che, durante il viaggio, almeno una volta hai viaggiato esattamente a 60 km/h, anche se per il resto del tempo potresti aver viaggiato più veloce o più lento.
Questo risultato è un'applicazione fisica fondamentale del Teorema di Lagrange e mostra come concetti matematici astratti abbiano rilevanti interpretazioni nel mondo reale. È anche alla base dei controlli automatici della velocità media (ad esempio sui tratti autostradali con sistema Tutor).
Mediante il teorema di Lagrange, dimostra che \(\forall a, b \in \mathbb{R}\) vale la disuguaglianza:
\[ |\sin(b) - \sin(a)| \leq |b - a| \]Soluzione quesito 8:
Dobbiamo dimostrare che per ogni \(a, b \in \mathbb{R}\) vale:
\[ |\sin(b) - \sin(a)| \leq |b - a| \]Consideriamo la funzione \(f(x) = \sin(x)\) e l'intervallo \([a, b]\) (supponiamo \(a < b\); il caso \(a > b\) è analogo).
La funzione \(f(x) = \sin(x)\):
Per il Teorema di Lagrange, esiste almeno un punto \(c \in (a, b)\) tale che:
\[ f'(c) = \frac{f(b) - f(a)}{b - a} \]cioè:
\[ \cos(c) = \frac{\sin(b) - \sin(a)}{b - a} \]Moltiplicando entrambi i membri per \(b - a > 0\):
\[ \sin(b) - \sin(a) = \cos(c) \cdot (b - a) \]Prendiamo il valore assoluto di entrambi i membri:
\[ |\sin(b) - \sin(a)| = |\cos(c)| \cdot |b - a| \]Sappiamo che per ogni \(x \in \mathbb{R}\):
\[ |\cos(x)| \leq 1 \]In particolare, \(|\cos(c)| \leq 1\).
Quindi:
\[ |\sin(b) - \sin(a)| = |\cos(c)| \cdot |b - a| \leq 1 \cdot |b - a| = |b - a| \]Abbiamo dimostrato che:
\[ |\sin(b) - \sin(a)| \leq |b - a| \quad \forall a, b \in \mathbb{R} \]La disuguaglianza è quindi verificata. ∎