Teoremi di Rolle, Lagrange, Cauchy e De l'Hospital

Enunciato e Significato Geometrico del Teorema di Rolle

Il **Teorema di Rolle** è uno dei pilastri del calcolo differenziale e fornisce una condizione sufficiente per l'esistenza di un punto in cui la derivata di una funzione è zero, cioè un punto stazionario.

Enunciato del Teorema di Rolle

Sia una funzione $f:[a,b] \to \mathbb{R}$ tale che:

1. $f$ è **continua** nell'intervallo chiuso $[a,b]$.
2. $f$ è **derivabile** nell'intervallo aperto $(a,b)$.
3. $f(a) = f(b)$ (i valori della funzione agli estremi dell'intervallo sono uguali).

Allora, esiste almeno un punto $c \in (a,b)$ tale che $f'(c) = 0$.

Significato Geometrico

Geometricamente, il Teorema di Rolle afferma che se una funzione continua e derivabile ha lo stesso valore agli estremi di un intervallo, allora esiste almeno un punto all'interno di quell'intervallo in cui la tangente al grafico della funzione è **orizzontale**. Questo punto corrisponde a un massimo relativo, un minimo relativo o un punto di flesso orizzontale.

Grafico del Teorema di Rolle con tangente orizzontale

Grafico Illustrativo (Indicazioni per l'immagine)

Immagina il grafico di una funzione che parte da un punto, sale, poi scende, e finisce alla stessa altezza del punto di partenza. Il teorema ti dice che ci deve essere almeno un "picco" o una "valle" (o un punto di flesso orizzontale) dove la curva è momentaneamente piatta.

Immagine: Una curva che inizia e finisce alla stessa altezza, mostrando una tangente orizzontale in un punto intermedio.

Esempi di Verifica del Teorema di Rolle

Esempio 1: Funzione che soddisfa tutte le condizioni

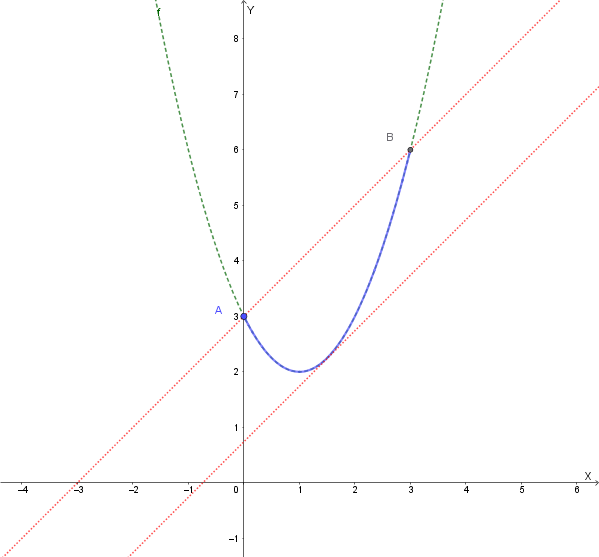
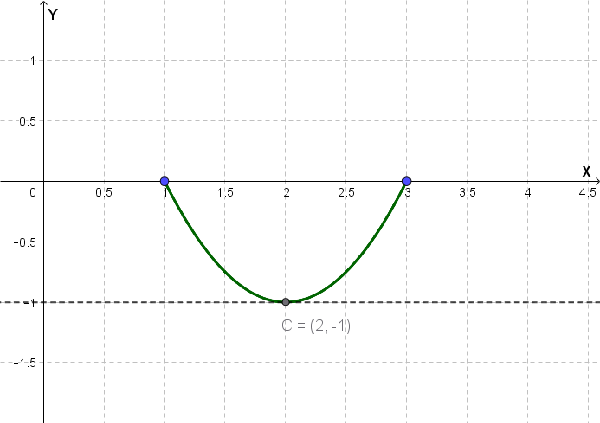
Verifichiamo il Teorema di Rolle per la funzione $f(x) = x^2 - 4x + 3$ nell'intervallo $[1,3]$.

1. Continuità:

$f(x) = x^2 - 4x + 3$ è una funzione polinomiale, quindi è continua su tutto $\mathbb{R}$, e in particolare nell'intervallo chiuso $[1,3]$.

2. Derivabilità:

$f(x)$ è una funzione polinomiale, quindi è derivabile su tutto $\mathbb{R}$. La sua derivata è $f'(x) = 2x - 4$, ed è definita in $(1,3)$.

3. Valori agli estremi:

$f(a) = f(1) = 1^2 - 4(1) + 3 = 1 - 4 + 3 = 0$
$f(b) = f(3) = 3^2 - 4(3) + 3 = 9 - 12 + 3 = 0$

Quindi, $f(1) = f(3) = 0$. La terza condizione è soddisfatta.

Poiché tutte le condizioni sono soddisfatte, il Teorema di Rolle garantisce l'esistenza di almeno un $c \in (1,3)$ tale che $f'(c) = 0$.

Ricerca del punto $c$:

Poniamo $f'(x) = 0$:

\[ 2x - 4 = 0 \] \[ 2x = 4 \] \[ x = 2 \]

Il punto $c=2$ appartiene all'intervallo $(1,3)$. Questo conferma il teorema.

**Grafico:** Grafico del Teorema di Rolle con parabola e tangente orizzontale

Esempio 2: Funzione con più punti $c$

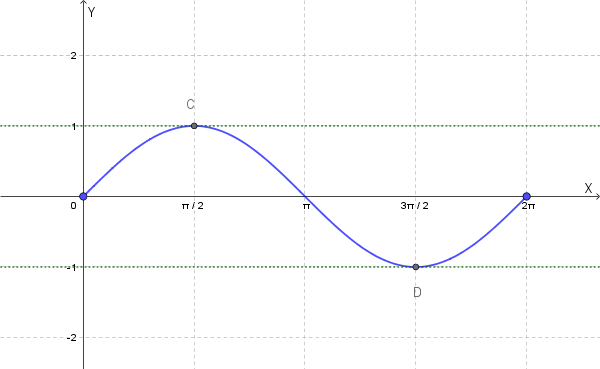
Verifichiamo il Teorema di Rolle per la funzione $f(x) = \sin(x)$ nell'intervallo $[0, 2\pi]$.

1. Continuità:

$f(x) = \sin(x)$ è continua su tutto $\mathbb{R}$, quindi anche in $[0, 2\pi]$.

2. Derivabilità:

$f(x) = \sin(x)$ è derivabile su tutto $\mathbb{R}$. La sua derivata è $f'(x) = \cos(x)$, ed è definita in $(0, 2\pi)$.

3. Valori agli estremi:

$f(a) = f(0) = \sin(0) = 0$
$f(b) = f(2\pi) = \sin(2\pi) = 0$

Quindi, $f(0) = f(2\pi) = 0$. La terza condizione è soddisfatta.

Tutte le condizioni sono soddisfatte, quindi esiste almeno un $c \in (0, 2\pi)$ tale che $f'(c) = 0$.

Ricerca dei punti $c$:

Poniamo $f'(x) = 0$:

\[ \cos(x) = 0 \]

Nell'intervallo $(0, 2\pi)$, i valori di $x$ per cui $\cos(x) = 0$ sono:

\[ x = \frac{\pi}{2} \quad \text{e} \quad x = \frac{3\pi}{2} \]

Entrambi i punti **$\frac{\pi}{2}$** e **$\frac{3\pi}{2}$** appartengono all'intervallo $(0, 2\pi)$. Questo dimostra che possono esistere più punti che soddisfano il teorema.

**Grafico:** Grafico della funzione seno con tangenti orizzontali in pi/2 e 3pi/2

Casi in cui le condizioni non sono soddisfatte

È importante capire che il Teorema di Rolle fornisce una condizione sufficiente, non necessaria. Se una o più condizioni non sono soddisfatte, il teorema non garantisce l'esistenza di un tale punto $c$, ma non lo esclude nemmeno a priori.

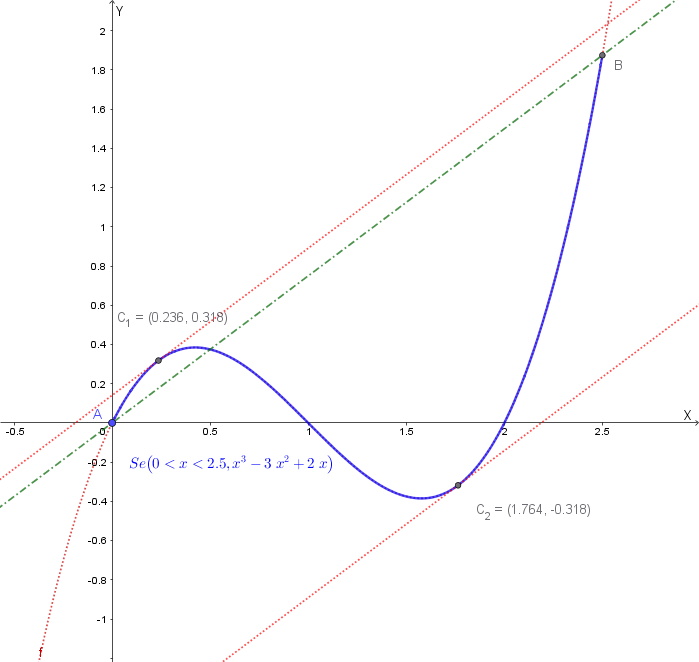
Esempio 3: Condizione di derivabilità non soddisfatta

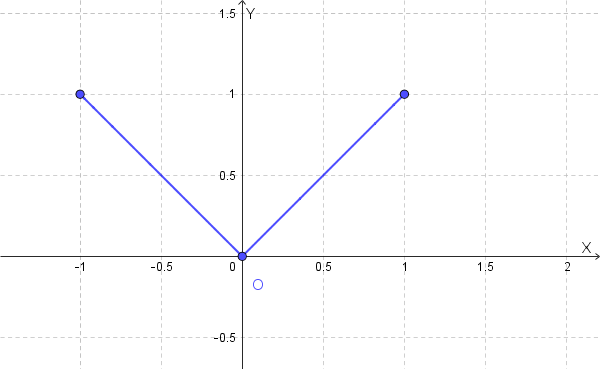
Consideriamo la funzione $f(x) = |x|$ nell'intervallo $[-1,1]$.

1. Continuità:

$f(x) = |x|$ è continua su tutto $\mathbb{R}$, quindi anche in $[-1,1]$.

2. Derivabilità:

$f(x) = |x|$ **non è derivabile** in $x=0$, che si trova all'interno dell'intervallo $(-1,1)$. C'è un "punto angoloso" nel grafico.

3. Valori agli estremi:

$f(a) = f(-1) = |-1| = 1$
$f(b) = f(1) = |1| = 1$

Quindi, $f(-1) = f(1)$. Questa condizione è soddisfatta.

Poiché la condizione di derivabilità non è soddisfatta, il Teorema di Rolle non si applica. E infatti, se calcoliamo la derivata (dove esiste), $f'(x) = 1$ per $x>0$ e $f'(x) = -1$ per $x<0$. Non esiste alcun punto $c \in (-1,1)$ tale che $f'(c) = 0$.

**Grafico:** Grafico del valore assoluto che non ha tangente orizzontale

Esempio 4: Condizione di continuità in un estremo non soddisfatta

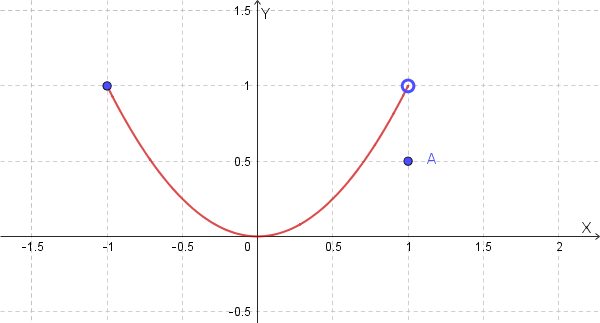
Consideriamo la funzione definita a tratti nell'intervallo $[-1, 1]$:

\[ f(x) = \begin{cases} x^2 & \text{se } -1 \le x < 1 \\ 1/2 & \text{se } x = 1 \end{cases} \]

1. Continuità:

La funzione $f(x) = x^2$ è continua per $-1 \le x < 1$. Tuttavia, dobbiamo verificare la continuità all'estremo $x=1$.

Il limite della funzione per $x \to 1^-$ è $\lim_{x \to 1^-} x^2 = 1^2 = 1$.

Il valore della funzione in $x=1$ è $f(1) = 1/2$.

Poiché $\lim_{x \to 1^-} f(x) \neq f(1)$, la funzione **non è continua** nell'intervallo chiuso $[-1,1]$ a causa della discontinuità in $x=1$.

2. Derivabilità:

Per $-1 < x < 1$, la funzione $f(x) = x^2$ è derivabile con $f'(x) = 2x$.

3. Valori agli estremi:

$f(a) = f(-1) = (-1)^2 = 1$
$f(b) = f(1) = 1/2$

Quindi, $f(-1) \neq f(1)$. Anche questa condizione **non è soddisfatta** a causa della discontinuità nell'estremo destro che cambia il valore $f(1)$.

(Anche se la condizione sui valori agli estremi non è soddisfatta per via della discontinuità, l'esempio serve a illustrare specificamente la rottura della continuità nell'estremo.)

Poiché la condizione di continuità nell'intervallo chiuso $[a,b]$ non è soddisfatta, il Teorema di Rolle non si applica. E in effetti, se calcoliamo la derivata $f'(x)=2x$ per $-1 < x < 1$, ponendo $f'(x)=0$ otteniamo $x=0$. Sebbene $c=0$ sia nell'intervallo aperto, il teorema non garantisce la sua esistenza in questo contesto a causa della violazione della condizione di continuità all'estremo.

**Grafico:** Grafico di una parabola con discontinuità in un estremo

Esempio 5: Condizione sui valori agli estremi non soddisfatta (funzione continua)

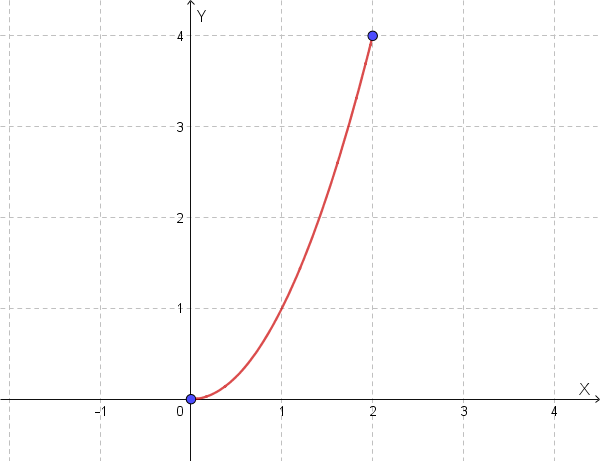
Consideriamo la funzione $f(x) = x^2$ nell'intervallo $[0,2]$.

1. Continuità:

$f(x) = x^2$ è continua in $[0,2]$.

2. Derivabilità:

$f(x)$ è derivabile in $(0,2)$, con $f'(x) = 2x$.

3. Valori agli estremi:

$f(a) = f(0) = 0^2 = 0$
$f(b) = f(2) = 2^2 = 4$

Quindi, $f(0) \neq f(2)$. La terza condizione **non è soddisfatta**.

Il Teorema di Rolle non si applica. Sebbene $f'(x) = 2x = 0$ implichi $x=0$, questo punto non appartiene all'intervallo aperto $(0,2)$. Quindi, in questo caso, non esiste un $c$ nell'intervallo aperto che soddisfi la condizione.

**Grafico:** Grafico di una parabola che non ha tangente orizzontale tra 0 e 2

Il **Teorema di Lagrange** è una generalizzazione del Teorema di Rolle e rappresenta uno degli enunciati più importanti del calcolo differenziale. Collega il comportamento locale (la derivata) di una funzione al suo comportamento globale (la differenza dei valori agli estremi dell'intervallo).

Enunciato del Teorema di Lagrange

Sia una funzione $f:[a,b] \to \mathbb{R}$ tale che:

1. $f$ è **continua** nell'intervallo chiuso $[a,b]$.
2. $f$ è **derivabile** nell'intervallo aperto $(a,b)$.

Allora, esiste almeno un punto $c \in (a,b)$ tale che:

\[ f'(c) = \frac{f(b) - f(a)}{b - a} \]

Commento all'Enunciato

A differenza del Teorema di Rolle, il Teorema di Lagrange non richiede che i valori della funzione agli estremi dell'intervallo siano uguali ($f(a)=f(b)$). Questo lo rende molto più applicabile in generale. La condizione chiave è che la funzione sia "ben comportata" nell'intervallo, cioè continua e derivabile.

La formula $f'(c) = \frac{f(b) - f(a)}{b - a}$ mette in relazione la pendenza della tangente alla curva in un punto $c$ con la pendenza della retta secante che congiunge i punti $(a, f(a))$ e $(b, f(b))$.

Significato Geometrico

Geometricamente, il Teorema di Lagrange afferma che se una funzione è continua in un intervallo chiuso e derivabile nell'intervallo aperto, allora esiste almeno un punto $c$ all'interno dell'intervallo in cui la tangente al grafico della funzione è **parallela** alla retta secante che unisce i punti $(a, f(a))$ e $(b, f(b))$.

Grafico Illustrativo

Immagina il grafico di una funzione tra due punti A e B. Traccia la retta che collega A e B (la retta secante). Il teorema ti dice che, da qualche parte lungo la curva tra A e B, ci deve essere un punto in cui la tangente al grafico è esattamente parallela a quella retta secante.

Immagine: Una curva tra (a, f(a)) e (b, f(b)) con una retta secante che li unisce. Una tangente alla curva in un punto c è parallela alla secante.

Grafico del Teorema di Lagrange con tangente parallela alla secante

Il Teorema di Rolle come Caso Particolare del Teorema di Lagrange

Il Teorema di Rolle può essere visto come un caso speciale del Teorema di Lagrange. Per capirlo, consideriamo le condizioni del Teorema di Rolle:

1. $f$ è continua in $[a,b]$.
2. $f$ è derivabile in $(a,b)$.
3. $f(a) = f(b)$.

Le prime due condizioni sono esattamente le stesse del Teorema di Lagrange. Se aggiungiamo la terza condizione ($f(a) = f(b)$), vediamo cosa succede all'uguaglianza del Teorema di Lagrange:

\[ f'(c) = \frac{f(b) - f(a)}{b - a} \]

Se $f(a) = f(b)$, allora il numeratore della frazione diventa $f(b) - f(a) = 0$. Quindi l'equazione diventa:

\[ f'(c) = \frac{0}{b - a} \] \[ f'(c) = 0 \]

Questo è esattamente l'enunciato del Teorema di Rolle! Ciò significa che se le condizioni di Rolle sono soddisfatte, allora la pendenza della retta secante è zero (la retta è orizzontale), e di conseguenza, la tangente in almeno un punto $c$ sarà anch'essa orizzontale.

Esempio 1: applicazione del Teorema di Lagrange all'Esempio di Rolle

Riprendiamo l'Esempio 1 del Teorema di Rolle: $f(x) = x^2 - 4x + 3$ nell'intervallo $[1,3]$.

1. Continuità: $f(x)$ è continua in $[1,3]$.

2. Derivabilità: $f(x)$ è derivabile in $(1,3)$.

Queste sono le condizioni di Lagrange. Troviamo il punto $c$ tale che $f'(c) = \frac{f(b) - f(a)}{b - a}$.

Calcolo di $f(a)$ e $f(b)$:

$f(1) = 1^2 - 4(1) + 3 = 0$
$f(3) = 3^2 - 4(3) + 3 = 0$

Quindi, $\frac{f(3) - f(1)}{3 - 1} = \frac{0 - 0}{2} = 0$.

Calcolo di $f'(x)$:

$f'(x) = 2x - 4$.

Trovare $c$:

Poniamo $f'(c) = 0$:

\[ 2c - 4 = 0 \] \[ 2c = 4 \] \[ c = 2 \]

Il punto $c=2$ appartiene all'intervallo $(1,3)$. In questo caso, la pendenza della secante è 0, e quindi il Teorema di Lagrange ci porta allo stesso risultato del Teorema di Rolle.

Immagine: Il grafico della parabola dell'esempio 1 di Rolle. Ora, la secante è l'asse x stesso, e la tangente orizzontale in c=2 è parallela a questa secante.

Esempio 2: Applicazione diretta del Teorema di Lagrange (Caso generale)

Verifichiamo il Teorema di Lagrange per la funzione $f(x) = x^3 - 3x^2 + 2x$ nell'intervallo $[0, \frac{5}{2}]$.

1. Continuità:

$f(x) = x^3 - 3x^2 + 2x$ è una funzione polinomiale, quindi è continua su tutto $\mathbb{R}$, e in particolare nell'intervallo chiuso $[0, \frac{5}{2}]$.

2. Derivabilità:

$f(x)$ è una funzione polinomiale, quindi è derivabile su tutto $\mathbb{R}$. La sua derivata è $f'(x) = 3x^2 - 6x + 2$, ed è definita in $(0, \frac{5}{2})$.

Poiché entrambe le condizioni sono soddisfatte, il Teorema di Lagrange garantisce l'esistenza di almeno un punto $c \in (0, \frac{5}{2})$ tale che $f'(c) = \frac{f(\frac{5}{2}) - f(0)}{\frac{5}{2} - 0}$.

Calcolo della pendenza della retta secante:

$f(a) = f(0) = 0^3 - 3(0)^2 + 2(0) = 0$
$f(b) = f(\frac{5}{2}) = (\frac{5}{2})^3 - 3(\frac{5}{2})^2 + 2(\frac{5}{2})$
$f(\frac{5}{2}) = \frac{125}{8} - 3(\frac{25}{4}) + 5 = \frac{125}{8} - \frac{75}{4} + 5$
$f(\frac{5}{2}) = \frac{125}{8} - \frac{150}{8} + \frac{40}{8} = \frac{125 - 150 + 40}{8} = \frac{15}{8}$

Quindi, la pendenza della secante è: $\frac{f(\frac{5}{2}) - f(0)}{\frac{5}{2} - 0} = \frac{\frac{15}{8} - 0}{\frac{5}{2}} = \frac{15}{8} \cdot \frac{2}{5} = \frac{3 \cdot 1}{4 \cdot 1} = \frac{3}{4}$.

Ci aspettiamo di trovare un $c \in (0, \frac{5}{2})$ tale che la pendenza della tangente sia $\frac{3}{4}$.

Ricerca del punto $c$:

Poniamo $f'(x) = \frac{3}{4}$:

\[ 3x^2 - 6x + 2 = \frac{3}{4} \] \[ 3x^2 - 6x + 2 - \frac{3}{4} = 0 \] \[ 3x^2 - 6x + \frac{8-3}{4} = 0 \] \[ 3x^2 - 6x + \frac{5}{4} = 0 \]

Moltiplichiamo tutto per 4 per eliminare la frazione:

\[ 12x^2 - 24x + 5 = 0 \]

Usiamo la formula risolutiva per le equazioni quadratiche $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$:

\[ x = \frac{-(-24) \pm \sqrt{(-24)^2 - 4(12)(5)}}{2(12)} \] \[ x = \frac{24 \pm \sqrt{576 - 240}}{24} \] \[ x = \frac{24 \pm \sqrt{336}}{24} \] \[ x = \frac{24 \pm \sqrt{16 \cdot 21}}{24} \] \[ x = \frac{24 \pm 4\sqrt{21}}{24} \] \[ x = \frac{6 \pm \sqrt{21}}{6} \]

Abbiamo due possibili valori per $c$:

$c_1 = \frac{6 - \sqrt{21}}{6} \approx \frac{6 - 4.58}{6} = \frac{1.42}{6} \approx 0.237$
$c_2 = \frac{6 + \sqrt{21}}{6} \approx \frac{6 + 4.58}{6} = \frac{10.58}{6} \approx 1.763$

Verifichiamo quali punti appartengono all'intervallo aperto $(0, \frac{5}{2})$ (cioè $(0, 2.5)$):

$c_1 \approx 0.237$ appartiene all'intervallo $(0, 2.5)$.
$c_2 \approx 1.763$ appartiene all'intervallo $(0, 2.5)$.

Entrambi i punti $c_1$ e $c_2$ soddisfano il teorema. In questi due punti, la tangente al grafico della funzione ha una pendenza pari a $\frac{3}{4}$, la stessa pendenza della retta secante che congiunge i punti $(0,0)$ e $(\frac{5}{2}, \frac{15}{8})$.

Enunciato e Spiegazione del Teorema di Cauchy (o del Valor Medio Generalizzato)

Il **Teorema di Cauchy** è una generalizzazione del Teorema di Lagrange e, di conseguenza, anche del Teorema di Rolle. È particolarmente utile come prerequisito per la dimostrazione della Regola di De l'Hospital.

Enunciato del Teorema di Cauchy

Siano due funzioni $f:[a,b] \to \mathbb{R}$ e $g:[a,b] \to \mathbb{R}$ tali che:

1. $f$ e $g$ sono **continue** nell'intervallo chiuso $[a,b]$.
2. $f$ e $g$ sono **derivabili** nell'intervallo aperto $(a,b)$.
3. $g'(x) \neq 0$ per ogni $x \in (a,b)$.

Allora, esiste almeno un punto $c \in (a,b)$ tale che:

\[ \frac{f'(c)}{g'(c)} = \frac{f(b) - f(a)}{g(b) - g(a)} \]

Spiegazione e Significato

Il Teorema di Cauchy mette in relazione i rapporti delle derivate delle due funzioni in un punto $c$ con i rapporti delle differenze dei valori delle funzioni agli estremi dell'intervallo. È come applicare il concetto di "valor medio" a due funzioni contemporaneamente.

Per capire la sua generalizzazione, pensa al Teorema di Lagrange. Se scegliamo $g(x) = x$, allora $g'(x) = 1$. Sostituendo nel Teorema di Cauchy otteniamo:

\[ \frac{f'(c)}{1} = \frac{f(b) - f(a)}{b - a} \]

Che è esattamente l'enunciato del Teorema di Lagrange. Questo dimostra che il Teorema di Lagrange è un caso particolare del Teorema di Cauchy quando una delle funzioni è semplicemente $g(x) = x$.

La condizione $g'(x) \neq 0$ è fondamentale per evitare divisioni per zero e garantire che $g(b) - g(a) \neq 0$. Se $g'(x)$ fosse zero in qualche punto, e $g(b) = g(a)$, si ricadrebbe in una situazione analoga a quella del Teorema di Rolle per $g(x)$.

Esempi di Verifica del Teorema di Cauchy

Esempio 1: Funzioni che soddisfano tutte le condizioni

Verifichiamo il Teorema di Cauchy per le funzioni $f(x) = x^2$ e $g(x) = x^3$ nell'intervallo $[1, 2]$.

1. Continuità:

$f(x) = x^2$ e $g(x) = x^3$ sono funzioni polinomiali, quindi sono continue su tutto $\mathbb{R}$, e in particolare nell'intervallo chiuso $[1, 2]$.

2. Derivabilità:

$f(x) = x^2$ è derivabile con $f'(x) = 2x$.

$g(x) = x^3$ è derivabile con $g'(x) = 3x^2$.

Entrambe sono derivabili nell'intervallo aperto $(1, 2)$.

3. Condizione $g'(x) \neq 0$:

In $(1, 2)$, $g'(x) = 3x^2$. Poiché $x \neq 0$ in questo intervallo, $3x^2 \neq 0$ per ogni $x \in (1,2)$. La condizione è soddisfatta.

Poiché tutte le condizioni sono soddisfatte, il Teorema di Cauchy garantisce l'esistenza di almeno un punto $c \in (1, 2)$ tale che $\frac{f'(c)}{g'(c)} = \frac{f(2) - f(1)}{g(2) - g(1)}$.

Calcolo del rapporto delle differenze agli estremi:

$f(1) = 1^2 = 1$
$f(2) = 2^2 = 4$
$g(1) = 1^3 = 1$
$g(2) = 2^3 = 8$

Quindi, $\frac{f(2) - f(1)}{g(2) - g(1)} = \frac{4 - 1}{8 - 1} = \frac{3}{7}$.

Calcolo del rapporto delle derivate:

$f'(x) = 2x$

$g'(x) = 3x^2$

Il rapporto è $\frac{f'(x)}{g'(x)} = \frac{2x}{3x^2} = \frac{2}{3x}$ (per $x \neq 0$).

Ricerca del punto $c$:

Poniamo il rapporto delle derivate uguale al rapporto delle differenze:

\[ \frac{2}{3c} = \frac{3}{7} \]

Risolviamo per $c$:

\[ 2 \cdot 7 = 3c \cdot 3 \] \[ 14 = 9c \] \[ c = \frac{14}{9} \]

Convertiamo in decimale per verificare l'intervallo: $c = \frac{14}{9} \approx 1.556$.

Il punto $c = \frac{14}{9}$ appartiene all'intervallo aperto $(1, 2)$ (poiché $1 < 1.556 < 2$). Questo conferma il teorema.

Casi in cui le condizioni non sono soddisfatte

Come per Rolle e Lagrange, se una o più condizioni del Teorema di Cauchy non sono soddisfatte, il teorema non garantisce l'esistenza di un punto $c$, ma non la esclude nemmeno a priori.

Esempio 2: Condizione $g'(x) \neq 0$ non soddisfatta

Consideriamo le funzioni $f(x) = x^2$ e $g(x) = x^3$ nell'intervallo $[-1, 1]$.

1. Continuità:

$f(x) = x^2$ e $g(x) = x^3$ sono continue su $[-1, 1]$.

2. Derivabilità:

$f'(x) = 2x$ e $g'(x) = 3x^2$. Entrambe sono derivabili in $(-1, 1)$.

3. Condizione $g'(x) \neq 0$:

In questo intervallo, $g'(x) = 3x^2$ è uguale a zero per $x=0$, che si trova all'interno dell'intervallo $(-1, 1)$. Quindi, la condizione $g'(x) \neq 0$ per ogni $x \in (a,b)$ **non è soddisfatta**.

Poiché una delle condizioni non è soddisfatta, il Teorema di Cauchy non è applicabile.

Introduzione ai Teoremi di De l'Hospital

I **Teoremi di De l'Hospital** (spesso chiamati anche Regola di L'Hôpital o de L'Hospital) sono strumenti fondamentali nel calcolo differenziale per il calcolo dei limiti di forme indeterminate. Sono particolarmente utili quando l'applicazione diretta dei limiti porta a espressioni del tipo $\frac{0}{0}$ o $\frac{\infty}{\infty}$.

Questi teoremi permettono di risolvere tali indeterminatezze derivando separatamente il numeratore e il denominatore della frazione.

1. Primo Teorema di De l'Hospital (Forma Indeterminata $\frac{0}{0}$)

Enunciato

Siano $f(x)$ e $g(x)$ due funzioni derivabili in un intervallo aperto $I$ contenente il punto $x_0$, e sia $g'(x) \neq 0$ per ogni $x \in I$, $x \neq x_0$. Se:

$\lim_{x \to x_0} f(x) = 0$
$\lim_{x \to x_0} g(x) = 0$

Allora, se esiste il limite del rapporto delle derivate, esiste anche il limite del rapporto delle funzioni, e si ha:

\[ \lim_{x \to x_0} \frac{f(x)}{g(x)} = \lim_{x \to x_0} \frac{f'(x)}{g'(x)} \]

Questo teorema vale anche per i limiti laterali ($x \to x_0^+$ o $x \to x_0^-$) e per i limiti all'infinito ($x \to \pm\infty$).

Esempio 1: Calcolo di un limite con forma $\frac{0}{0}$

Calcoliamo il limite: $\lim_{x \to 0} \frac{e^x - 1}{x}$.

1. Verifica delle ipotesi e della forma indeterminata:

Le funzioni $f(x) = e^x - 1$ e $g(x) = x$ sono continue e derivabili su tutto $\mathbb{R}$. Inoltre, $g'(x) = 1 \neq 0$ per ogni $x$. Verifichiamo la forma indeterminata:

$\lim_{x \to 0} (e^x - 1) = e^0 - 1 = 1 - 1 = 0$
$\lim_{x \to 0} x = 0$

Siamo nella forma indeterminata $\frac{0}{0}$. Poiché le ipotesi sono verificate, possiamo applicare il Teorema di De l'Hospital.

2. Applicazione del Teorema di De l'Hospital:

Deriviamo numeratore e denominatore:

$f(x) = e^x - 1 \implies f'(x) = e^x$
$g(x) = x \implies g'(x) = 1$

Applichiamo il teorema:

\[ \lim_{x \to 0} \frac{e^x - 1}{x} = \lim_{x \to 0} \frac{e^x}{1} \]

3. Calcolo del nuovo limite: \[ \lim_{x \to 0} \frac{e^x}{1} = \frac{e^0}{1} = \frac{1}{1} = 1 \]

Quindi, $\lim_{x \to 0} \frac{e^x - 1}{x} = 1$.

Esempio 2: Altro limite con forma $\frac{0}{0}$

Calcoliamo il limite: $\lim_{x \to 1} \frac{\ln(x)}{x-1}$.

1. Verifica delle ipotesi e della forma indeterminata:

Le funzioni $f(x) = \ln(x)$ e $g(x) = x-1$ sono continue e derivabili nel loro dominio. In particolare, $g'(x) = 1 \neq 0$ per ogni $x$. Verifichiamo la forma indeterminata:

$\lim_{x \to 1} \ln(x) = \ln(1) = 0$
$\lim_{x \to 1} (x-1) = 1-1 = 0$

Siamo nella forma indeterminata $\frac{0}{0}$. Poiché le ipotesi sono verificate, possiamo applicare il Teorema di De l'Hospital.

2. Applicazione del Teorema di De l'Hospital:

$f(x) = \ln(x) \implies f'(x) = \frac{1}{x}$
$g(x) = x-1 \implies g'(x) = 1$

Applichiamo il teorema:

\[ \lim_{x \to 1} \frac{\ln(x)}{x-1} = \lim_{x \to 1} \frac{\frac{1}{x}}{1} \]

3. Calcolo del nuovo limite: \[ \lim_{x \to 1} \frac{\frac{1}{x}}{1} = \frac{\frac{1}{1}}{1} = \frac{1}{1} = 1 \]

Quindi, $\lim_{x \to 1} \frac{\ln(x)}{x-1} = 1$.

2. Secondo Teorema di De l'Hospital (Forma Indeterminata $\frac{\infty}{\infty}$)

Enunciato

Siano $f(x)$ e $g(x)$ due funzioni derivabili in un intervallo aperto $I$ contenente il punto $x_0$, e sia $g'(x) \neq 0$ per ogni $x \in I$, $x \neq x_0$. Se:

$\lim_{x \to x_0} f(x) = \pm\infty$
$\lim_{x \to x_0} g(x) = \pm\infty$

Allora, se esiste il limite del rapporto delle derivate, esiste anche il limite del rapporto delle funzioni, e si ha:

\[ \lim_{x \to x_0} \frac{f(x)}{g(x)} = \lim_{x \to x_0} \frac{f'(x)}{g'(x)} \]

Anche questo teorema vale per i limiti laterali ($x \to x_0^+$ o $x \to x_0^-$) e per i limiti all'infinito ($x \to \pm\infty$).

Esempio 1: Calcolo di un limite con forma $\frac{\infty}{\infty}$

Calcoliamo il limite: $\lim_{x \to +\infty} \frac{e^x}{x}$.

1. Verifica delle ipotesi e della forma indeterminata:

Le funzioni $f(x) = e^x$ e $g(x) = x$ sono continue e derivabili su $\mathbb{R}$. In particolare, $g'(x) = 1 \neq 0$ per ogni $x$. Verifichiamo la forma indeterminata:

$\lim_{x \to +\infty} e^x = +\infty$
$\lim_{x \to +\infty} x = +\infty$

Siamo nella forma indeterminata $\frac{\infty}{\infty}$. Poiché le ipotesi sono verificate, possiamo applicare il Teorema di De l'Hospital.

2. Applicazione del Teorema di De l'Hospital:

$f(x) = e^x \implies f'(x) = e^x$
$g(x) = x \implies g'(x) = 1$

Applichiamo il teorema:

\[ \lim_{x \to +\infty} \frac{e^x}{x} = \lim_{x \to +\infty} \frac{e^x}{1} \]

3. Calcolo del nuovo limite: \[ \lim_{x \to +\infty} \frac{e^x}{1} = +\infty \]

Quindi, $\lim_{x \to +\infty} \frac{e^x}{x} = +\infty$. (Questo mostra che $e^x$ cresce molto più velocemente di $x$).

Esempio 2: Altro limite con forma $\frac{\infty}{\infty}$

Calcoliamo il limite: $\lim_{x \to +\infty} \frac{\ln(x)}{x}$.

1. Verifica delle ipotesi e della forma indeterminata:

Le funzioni $f(x) = \ln(x)$ e $g(x) = x$ sono continue e derivabili per $x > 0$. In particolare, $g'(x) = 1 \neq 0$ per ogni $x$. Verifichiamo la forma indeterminata:

$\lim_{x \to +\infty} \ln(x) = +\infty$
$\lim_{x \to +\infty} x = +\infty$

Siamo nella forma indeterminata $\frac{\infty}{\infty}$. Poiché le ipotesi sono verificate, possiamo applicare il Teorema di De l'Hospital.

2. Applicazione del Teorema di De l'Hospital:

$f(x) = \ln(x) \implies f'(x) = \frac{1}{x}$
$g(x) = x \implies g'(x) = 1$

Applichiamo il teorema:

\[ \lim_{x \to +\infty} \frac{\ln(x)}{x} = \lim_{x \to +\infty} \frac{\frac{1}{x}}{1} \]

3. Calcolo del nuovo limite: \[ \lim_{x \to +\infty} \frac{\frac{1}{x}}{1} = \lim_{x \to +\infty} \frac{1}{x} = 0 \]

Quindi, $\lim_{x \to +\infty} \frac{\ln(x)}{x} = 0$. (Questo mostra che $x$ cresce molto più velocemente di $\ln(x)$).

Gestione di Altre Forme Indeterminate con De l'Hospital

I teoremi di De l'Hospital sono applicabili direttamente solo alle forme $\frac{0}{0}$ e $\frac{\infty}{\infty}$. Tuttavia, altre forme indeterminate possono essere trasformate algebricamente per ricadere in una di queste due categorie.

Esempio: Forma Indeterminata $0 \cdot \infty$

Calcoliamo il limite: $\lim_{x \to 0^+} x \ln(x)$.

1. Verifica della forma indeterminata e trasformazione:

$\lim_{x \to 0^+} x = 0$
$\lim_{x \to 0^+} \ln(x) = -\infty$

Siamo nella forma indeterminata $0 \cdot (-\infty)$. Per applicare De l'Hospital, trasformiamo il prodotto in un quoziente. Scegliamo la forma che porta a $\frac{-\infty}{\infty}$:

\[ \lim_{x \to 0^+} x \ln(x) = \lim_{x \to 0^+} \frac{\ln(x)}{\frac{1}{x}} \]

Le funzioni $f(x) = \ln(x)$ e $g(x) = \frac{1}{x}$ sono continue e derivabili per $x > 0$. Inoltre, $g'(x) = -\frac{1}{x^2} \neq 0$ per $x \neq 0$. Verifichiamo la forma indeterminata per la nuova espressione:

$\lim_{x \to 0^+} \ln(x) = -\infty$
$\lim_{x \to 0^+} \frac{1}{x} = +\infty$

Siamo nella forma indeterminata $\frac{-\infty}{\infty}$. Poiché le ipotesi sono verificate, possiamo applicare il Teorema di De l'Hospital.

2. Applicazione del Teorema di De l'Hospital:

Deriviamo numeratore e denominatore:

$f(x) = \ln(x) \implies f'(x) = \frac{1}{x}$
$g(x) = \frac{1}{x} = x^{-1} \implies g'(x) = -x^{-2} = -\frac{1}{x^2}$

Applichiamo il teorema:

\[ \lim_{x \to 0^+} \frac{\ln(x)}{\frac{1}{x}} = \lim_{x \to 0^+} \frac{\frac{1}{x}}{-\frac{1}{x^2}} \]

3. Semplificazione e calcolo del nuovo limite: \[ \lim_{x \to 0^+} \frac{\frac{1}{x}}{-\frac{1}{x^2}} = \lim_{x \to 0^+} \left( \frac{1}{x} \cdot \left(-\frac{x^2}{1}\right) \right) = \lim_{x \to 0^+} (-x) \] \[ \lim_{x \to 0^+} (-x) = 0 \]

Quindi, $\lim_{x \to 0^+} x \ln(x) = 0$.

Note Importanti sull'uso di De l'Hospital

**Verificare sempre la forma indeterminata:** De l'Hospital può essere applicato solo alle forme $\frac{0}{0}$ e $\frac{\infty}{\infty}$. Applicarlo ad altre forme porterà a risultati errati.
**Derivare separatamente:** Si devono derivare il numeratore e il denominatore singolarmente, non la frazione come quoziente.
**Applicazioni ripetute:** Se dopo la prima applicazione si ottiene ancora una forma indeterminata ($0/0$ o $\infty/\infty$), si può applicare la regola di De l'Hospital più volte, finché non si arriva a un limite risolvibile.
**Altre forme indeterminate:** Altre forme indeterminate come $0 \cdot \infty$, $\infty - \infty$, $1^\infty$, $0^0$, $\infty^0$ possono spesso essere ricondotte a $\frac{0}{0}$ o $\frac{\infty}{\infty}$ attraverso manipolazioni algebriche (es. trasformando prodotti in quozienti, usando logaritmi per le forme esponenziali).

Teoremi di Rolle, Lagrange, Cauchy e De l'Hospital

Enunciato e Significato Geometrico del Teorema di Rolle

Enunciato del Teorema di Rolle

Significato Geometrico

Grafico Illustrativo (Indicazioni per l'immagine)

Esempi di Verifica del Teorema di Rolle

Esempio 1: Funzione che soddisfa tutte le condizioni

Esempio 2: Funzione con più punti \(c\)

Casi in cui le condizioni non sono soddisfatte

Esempio 3: Condizione di derivabilità non soddisfatta

Esempio 4: Condizione di continuità in un estremo non soddisfatta

Esempio 5: Condizione sui valori agli estremi non soddisfatta (funzione continua)

Enunciato del Teorema di Lagrange

Commento all'Enunciato

Significato Geometrico

Grafico Illustrativo

Il Teorema di Rolle come Caso Particolare del Teorema di Lagrange

Esempio 1: applicazione del Teorema di Lagrange all'Esempio di Rolle

Esempio 2: Applicazione diretta del Teorema di Lagrange (Caso generale)

Enunciato e Spiegazione del Teorema di Cauchy (o del Valor Medio Generalizzato)

Enunciato del Teorema di Cauchy

Spiegazione e Significato

Esempi di Verifica del Teorema di Cauchy

Esempio 1: Funzioni che soddisfano tutte le condizioni

Casi in cui le condizioni non sono soddisfatte

Esempio 2: Condizione \(g'(x) \neq 0\) non soddisfatta

Introduzione ai Teoremi di De l'Hospital

1. Primo Teorema di De l'Hospital (Forma Indeterminata $\frac{0}{0}$)

Enunciato

Esempio 1: Calcolo di un limite con forma $\frac{0}{0}$

Esempio 2: Altro limite con forma $\frac{0}{0}$

2. Secondo Teorema di De l'Hospital (Forma Indeterminata $\frac{\infty}{\infty}$)

Enunciato

Esempio 1: Calcolo di un limite con forma $\frac{\infty}{\infty}$

Esempio 2: Altro limite con forma $\frac{\infty}{\infty}$

Gestione di Altre Forme Indeterminate con De l'Hospital

Esempio: Forma Indeterminata $0 \cdot \infty$

Note Importanti sull'uso di De l'Hospital