

Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.


Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
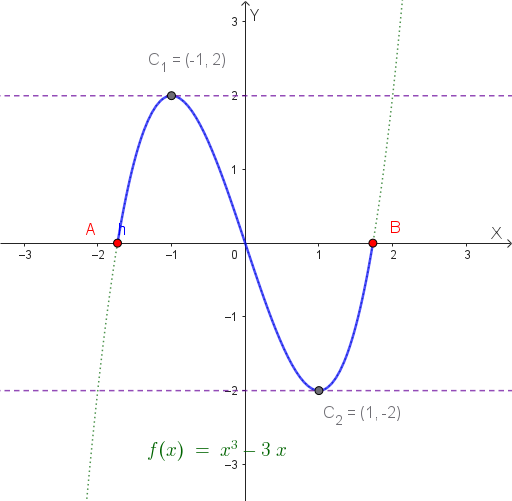
Considera la funzione \( f(x) = x^3 - 3x \) nell'intervallo \( [-\sqrt{3}, \sqrt{3}] \).
Soluzione quesito 1:
Il Teorema di Rolle afferma che se una funzione \( f(x) \):
allora esiste almeno un punto \( c \in (a, b) \) tale che \( f'(c) = 0 \).
Ipotesi 1 - Continuità:
La funzione \( f(x) = x^3 - 3x \) è un polinomio, quindi è continua su tutto \(\mathbb{R}\), e in particolare è continua nell'intervallo \([-\sqrt{3}, \sqrt{3}]\). ✓
Ipotesi 2 - Derivabilità:
Essendo un polinomio, \( f(x) \) è derivabile su tutto \(\mathbb{R}\), quindi è derivabile nell'intervallo aperto \((-\sqrt{3}, \sqrt{3})\). ✓
Ipotesi 3 - Valori uguali agli estremi:
Calcoliamo i valori della funzione agli estremi:
\[ f(-\sqrt{3}) = (-\sqrt{3})^3 - 3(-\sqrt{3}) = -3\sqrt{3} + 3\sqrt{3} = 0 \] \[ f(\sqrt{3}) = (\sqrt{3})^3 - 3\sqrt{3} = 3\sqrt{3} - 3\sqrt{3} = 0 \]Quindi \( f(-\sqrt{3}) = f(\sqrt{3}) = 0 \). ✓
Conclusione: Tutte e tre le ipotesi del Teorema di Rolle sono soddisfatte, quindi esiste almeno un punto \( c \in (-\sqrt{3}, \sqrt{3}) \) tale che \( f'(c) = 0 \).
Calcoliamo la derivata della funzione:
\[ f'(x) = \frac{d}{dx}(x^3 - 3x) = 3x^2 - 3 \]Risolviamo l'equazione \( f'(c) = 0 \):
\[ 3c^2 - 3 = 0 \] \[ 3c^2 = 3 \] \[ c^2 = 1 \] \[ c = \pm 1 \]Verifichiamo che entrambi i punti appartengano all'intervallo aperto \((-\sqrt{3}, \sqrt{3})\):
Poiché \(\sqrt{3} \approx 1.732\), abbiamo che: \[ -1.732 < -1 < 1 < 1.732 \] Quindi entrambi i punti \( c_1 = -1 \) e \( c_2 = 1 \) appartengono all'intervallo \((-\sqrt{3}, \sqrt{3})\).
Il Teorema di Rolle garantisce l'esistenza di punti in cui la tangente al grafico è orizzontale. Nel nostro caso, abbiamo trovato due punti: \( c = -1 \) e \( c = 1 \).
Geometricamente, questo significa che la funzione \( f(x) = x^3 - 3x \), partendo dal valore 0 in \( x = -\sqrt{3} \) e ritornando a 0 in \( x = \sqrt{3} \), deve necessariamente avere almeno un punto di massimo e un punto di minimo locale all'interno dell'intervallo, dove la derivata si annulla.
Risultato finale:
I punti che soddisfano la tesi del Teorema di Rolle sono: \[ c_1 = -1 \quad \text{e} \quad c_2 = 1 \]
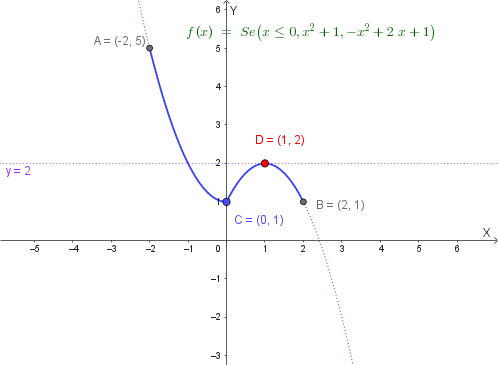
Stabilisci se la seguente funzione:
\[ f(x) = \begin{cases} x^2 + 1 & \text{se } x \leq 0 \\[10pt] -x^2 + 2x + 1 & \text{se } x > 0 \end{cases} \]soddisfa le ipotesi del Teorema di Rolle nell'intervallo \([-2, 2]\) e, in caso affermativo, determina tutti i punti \( c \) che soddisfano la tesi del teorema, cioè per cui \( f'(c) = 0 \).
Soluzione quesito 2:
Il Teorema di Rolle richiede che la funzione \( f(x) \):
Ipotesi 1 - Continuità in \([-2, 2]\):
La funzione è definita per casi. Dobbiamo verificare la continuità in tutto l'intervallo, in particolare nel punto di raccordo \(x = 0\).
Per \(x < 0\): \(f(x) = x^2 + 1\) è un polinomio, quindi continua.
Per \(x > 0\): \(f(x) = -x^2 + 2x + 1\) è un polinomio, quindi continua.
Verifichiamo la continuità in \(x = 0\):
\[ \lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} (x^2 + 1) = 0 + 1 = 1 \] \[ \lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} (-x^2 + 2x + 1) = 0 + 0 + 1 = 1 \] \[ f(0) = 0^2 + 1 = 1 \]Poiché \(\lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0) = 1\), la funzione è continua in \(x = 0\) e quindi in tutto \([-2, 2]\). ✓
Ipotesi 2 - Derivabilità in \((-2, 2)\):
La funzione è derivabile nei tratti \(x < 0\) e \(x > 0\) perché è un polinomio in entrambi i casi. Dobbiamo verificare la derivabilità nel punto di raccordo \(x = 0\).
Calcoliamo le derivate nei due rami:
Per \(x < 0\): \(f(x) = x^2 + 1\) quindi \(f'(x) = 2x\)
Per \(x > 0\): \(f(x) = -x^2 + 2x + 1\) quindi \(f'(x) = -2x + 2\)
Calcoliamo la derivata sinistra in \(x = 0\):
\[ f'_-(0) = \lim_{x \to 0^-} 2x = 0 \]Calcoliamo la derivata destra in \(x = 0\):
\[ f'_+(0) = \lim_{x \to 0^+} (-2x + 2) = 2 \]Poiché \(f'_-(0) = 0 \neq 2 = f'_+(0)\), la funzione non è derivabile in \(x = 0\). ✗
La funzione non soddisfa le ipotesi del Teorema di Rolle perché Non è derivabile in \(x = 0\) (punto interno all'intervallo).
Di conseguenza, il Teorema di Rolle non può essere applicato e non è detto che esistano punti \(c \in (-2, 2)\) tali che \(f'(c) = 0\).
Anche se il teorema non si applica, possono esserci comunque punti a tangente orizzontale, dove la derivata si annulla:
Nel tratto \(x < 0\): \(f'(x) = 2x = 0\) implica \(x = 0\), ma questo è il punto di non derivabilità.
Nel tratto \(x > 0\): \(f'(x) = -2x + 2 = 0\) implica \(x = 1\).
Quindi esiste un punto \(c = 1 \in (0, 2)\) dove \(f'(1) = 0\), ma questa informazione non è garantita dal Teorema di Rolle poiché non tutte le ipotesi sono soddisfatte.
Interpretazione geometrica:
In \(x = 0\) la funzione presenta un punto angoloso (anche se è continua): la tangente sinistra ha pendenza 0, mentre la tangente destra ha pendenza 2. Questo "spigolo" nella curva impedisce l'applicazione del Teorema di Rolle.
Determinare il dominio della funzione \[ f(x) = \ln\left(\frac{ax - 7}{x^2}\right) \] con \(a\) parametro reale positivo.
Successivamente, individuare il valore di \(a\) in corrispondenza del quale risultano soddisfatte le ipotesi del Teorema di Rolle nell'intervallo \([1, 7]\) e le coordinate del punto che ne verifica la tesi.
Soluzione quesito 3:
Affinché la funzione sia definita, l'argomento del logaritmo deve essere positivo:
\[ \frac{ax - 7}{x^2} > 0 \]Poiché \(x^2 > 0\) per ogni \(x \neq 0\), la disequazione si riduce a:
\[ ax - 7 > 0 \]Essendo \(a > 0\) (per ipotesi), possiamo dividere per \(a\):
\[ x > \frac{7}{a} \]Dominio: \(D = \left(\frac{7}{a}, +\infty\right)\) con \(a > 0\).
La funzione è continua e derivabile per ogni \(x > \frac{7}{a}\) con \(a > 0\).
Affinché valga il Teorema di Rolle nell'intervallo \([1, 7]\), dobbiamo verificare che:
Imponiamo \(f(1) = f(7)\):
\[ \ln\left(\frac{a \cdot 1 - 7}{1^2}\right) = \ln\left(\frac{a \cdot 7 - 7}{7^2}\right) \] \[ \ln(a - 7) = \ln\left(\frac{7a - 7}{49}\right) \]Deve quindi essere:
\[ a - 7 = \frac{7a - 7}{49} \]Moltiplichiamo entrambi i membri per 49:
\[ 49(a - 7) = 7a - 7 \] \[ 49a - 343 = 7a - 7 \] \[ 49a - 7a = 343 - 7 \] \[ 42a = 336 \] \[ a = 8 \]Verifichiamo che \(a = 8 > 7\), quindi la condizione sul dominio è soddisfatta. ✓
La funzione diventa:
\[ f(x) = \ln\left(\frac{8x - 7}{x^2}\right) \]che è definita, continua e derivabile per \(x > \frac{7}{8}\).
Quindi, per \(a = 8\), la funzione nell'intervallo \([1, 7]\) soddisfa le tre ipotesi del Teorema di Rolle:
Esiste quindi almeno un punto \(c\) interno all'intervallo dato in cui \(f'(c) = 0\).
Calcoliamo la derivata di \(f(x) = \ln\left(\frac{8x - 7}{x^2}\right)\):
\[ f'(x) = \frac{1}{\frac{8x - 7}{x^2}} \cdot \frac{d}{dx}\left(\frac{8x - 7}{x^2}\right) \]Calcoliamo la derivata del rapporto usando la regola del quoziente:
\[ \frac{d}{dx}\left(\frac{8x - 7}{x^2}\right) = \frac{8 \cdot x^2 - (8x - 7) \cdot 2x}{x^4} = \frac{8x^2 - 16x^2 + 14x}{x^4} = \frac{-8x^2 + 14x}{x^4} \]Quindi:
\[ f'(x) = \frac{x^2}{8x - 7} \cdot \frac{-8x^2 + 14x}{x^4} = \frac{-8x^2 + 14x}{x^2(8x - 7)} \]Risolviamo \(f'(x) = 0\):
\[ \frac{-8x^2 + 14x}{x^2(8x - 7)} = 0 \]Il numeratore deve annullarsi:
\[ -8x^2 + 14x = 0 \] \[ x(-8x + 14) = 0 \]Le soluzioni sono:
\[ x = 0 \quad \text{(non accettabile, fuori dal dominio)} \] \[ x = \frac{14}{8} = \frac{7}{4} \]Verifichiamo che \(c = \frac{7}{4} \in (1, 7)\): infatti \(1 < 1.75 < 7\). ✓
Calcoliamo \(f\left(\frac{7}{4}\right)\):
\[ f\left(\frac{7}{4}\right) = \ln\left(\frac{8 \cdot \frac{7}{4} - 7}{\left(\frac{7}{4}\right)^2}\right) = \ln\left(\frac{14 - 7}{\frac{49}{16}}\right) = \ln\left(\frac{7}{\frac{49}{16}}\right) = \ln\left(\frac{7 \cdot 16}{49}\right) = \ln\left(\frac{112}{49}\right) = \ln\left(\frac{16}{7}\right) \]Risultato finale:
Le coordinate del punto che soddisfa il Teorema di Rolle nell'intervallo \([1, 7]\) sono:
\[ \left(\frac{7}{4}, \ln\left(\frac{16}{7}\right)\right) \]Utilizzando il Teorema di Rolle, provare che tra due radici reali dell'equazione \(e^x \sin x = 1\) c'è almeno una radice reale dell'equazione \(e^x \cos x = -1\).
Soluzione quesito 4:
Siano \(a\) e \(b\) due radici reali dell'equazione \(e^x \sin x - 1 = 0\).
Consideriamo la funzione:
\[ f(x) = e^x \sin x - 1 \]La funzione \(f(x) = e^x \sin x - 1\) soddisfa le ipotesi del Teorema di Rolle nell'intervallo chiuso e limitato \([a, b]\):
Esiste quindi almeno un punto \(c\) interno all'intervallo \([a, b]\) in cui la derivata della funzione \(f(x)\) si annulla.
Ma risulta:
\[ f'(x) = e^x \sin x + e^x \cos x \]Poiché \(e^x \sin x = 1\), possiamo scrivere:
\[ f'(x) = 1 + e^x \cos x \]Esiste quindi almeno un valore \(c \in (a, b)\) che annulla \(1 + e^c \cos c\), cioè esiste almeno una radice reale dell'equazione:
\[ 1 + e^x \cos x = 0 \]che equivale a:
\[ e^x \cos x = -1 \]Dimostrazione completata:
Tra due radici reali dell'equazione \(e^x \sin x = 1\) c'è almeno una radice reale dell'equazione \(e^x \cos x = -1\).
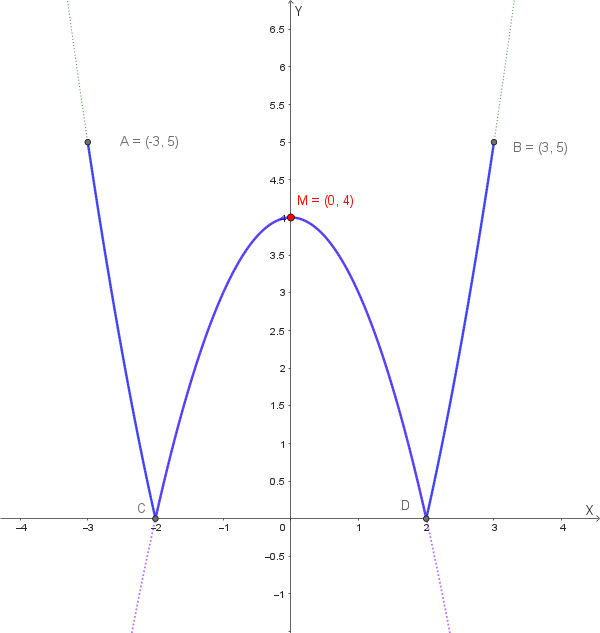
Data la funzione \( f(x) = |4 - x^2| \), verificare che essa non soddisfa tutte le ipotesi del Teorema di Rolle nell'intervallo \([-3, 3]\) e che comunque esiste almeno un punto dell'intervallo \((-3, 3)\) in cui la derivata prima di \(f(x)\) si annulla.
Questo esempio contraddice il Teorema di Rolle? Motivare la risposta in maniera esauriente.
Soluzione quesito 5:
La funzione \( f(x) = |4 - x^2| \) può essere scritta esplicitamente come:
\[ f(x) = \begin{cases} 4 - x^2 & \text{se } |x| \leq 2 \\[8pt] x^2 - 4 & \text{se } |x| > 2 \end{cases} \]ovvero:
\[ f(x) = \begin{cases} x^2 - 4 & \text{se } x < -2 \\[8pt] 4 - x^2 & \text{se } -2 \leq x \leq 2 \\[8pt] x^2 - 4 & \text{se } x > 2 \end{cases} \]Ipotesi 1 - Continuità in \([-3, 3]\):
La funzione valore assoluto è continua, e \(4 - x^2\) è continua, quindi \(f(x) = |4 - x^2|\) è continua su tutto \(\mathbb{R}\), e in particolare in \([-3, 3]\). ✓
Ipotesi 2 - Derivabilità in \((-3, 3)\):
La funzione non è derivabile nei punti in cui l'argomento del valore assoluto si annulla, cioè dove \(4 - x^2 = 0\):
\[ 4 - x^2 = 0 \quad \Rightarrow \quad x^2 = 4 \quad \Rightarrow \quad x = \pm 2 \]I punti \(x = -2\) e \(x = 2\) sono interni all'intervallo \((-3, 3)\), quindi la funzione non è derivabile in tutto l'intervallo aperto \((-3, 3)\). ✗
Ipotesi 3 - Valori uguali agli estremi:
Calcoliamo i valori agli estremi:
\[ f(-3) = |4 - (-3)^2| = |4 - 9| = |-5| = 5 \] \[ f(3) = |4 - 3^2| = |4 - 9| = |-5| = 5 \]Quindi \(f(-3) = f(3) = 5\). ✓
Conclusione sulle ipotesi:
La funzione soddisfa due delle tre ipotesi (continuità e valori uguali agli estremi), ma non è derivabile in \(x = -2\) e \(x = 2\), quindi non soddisfa tutte le ipotesi del Teorema di Rolle.
Calcoliamo la derivata nei tratti in cui la funzione è derivabile:
Cerchiamo dove \(f'(x) = 0\):
Quindi esiste almeno un punto, \(x = 0 \in (-3, 3)\), in cui la derivata si annulla. Questo punto corrisponde a un punto di massimo relativo del grafico, dove la tangente è orizzontale.
Il grafico della funzione si ottiene dalla parabola \(y = 4 - x^2\):
Nei punti \(x = -2\) e \(x = 2\) si formano dei punti angolosi (cuspidi verso il basso), dove la funzione non è derivabile.
In \(x = 0\) la funzione ha un massimo con tangente orizzontale, quindi \(f'(0) = 0\).
No, questo esempio NON contraddice il Teorema di Rolle.
Il Teorema di Rolle fornisce delle condizioni sufficienti (ma non necessarie) per garantire l'esistenza di almeno un punto in cui la derivata si annulla.
In altre parole:
Nel nostro esempio, anche se non tutte le ipotesi del Teorema di Rolle sono verificate (manca la derivabilità in \(x = \pm 2\)), esiste comunque un punto \(x = 0\) in cui la derivata si annulla. Questo è perfettamente compatibile con il teorema, che non esclude tale possibilità.
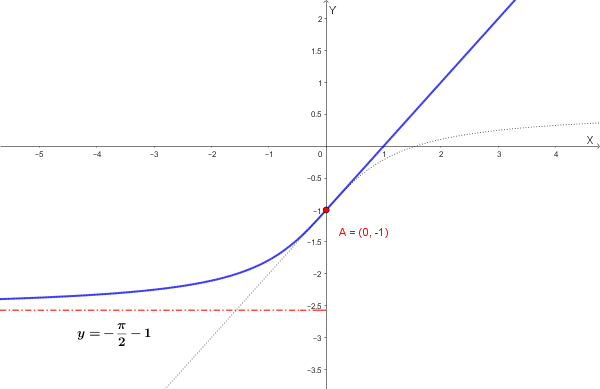
Si consideri la funzione:
\[ f(x) = \begin{cases} -1 + \arctan x & \text{se } x < 0 \\[8pt] ax + b & \text{se } x \geq 0 \end{cases} \]Determinare per quali valori dei parametri reali \(a\), \(b\) la funzione è derivabile.
Stabilire se esiste un intervallo di \(\mathbb{R}\) in cui la funzione \(f\) soddisfa le ipotesi del Teorema di Rolle. Motivare la risposta.
Soluzione quesito 6:
Osserviamo che per ogni \(x \neq 0\) la funzione è continua e derivabile, essendo formata da funzioni elementari sempre continue e derivabili nel loro dominio.
Il punto critico da analizzare è \(x = 0\).
Per essere derivabile in \(x = 0\), è necessario che la funzione sia prima di tutto continua in tale punto.
Calcoliamo i limiti e il valore della funzione:
\[ \lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} (-1 + \arctan x) = -1 + \arctan(0) = -1 + 0 = -1 \] \[ \lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} (ax + b) = a \cdot 0 + b = b \] \[ f(0) = a \cdot 0 + b = b \]Affinché la funzione sia continua in \(x = 0\), deve essere:
\[ \lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0) \] \[ -1 = b = b \]Quindi la funzione è continua in \(x = 0\) se e solo se \(b = -1\).
Calcoliamo la derivata nei due rami (assumendo \(b = -1\) per la continuità):
\[ f'(x) = \begin{cases} \dfrac{1}{1 + x^2} & \text{se } x < 0 \\[12pt] a & \text{se } x > 0 \end{cases} \]Calcoliamo le derivate destra e sinistra in \(x = 0\):
\[ f'_-(0) = \lim_{x \to 0^-} \frac{1}{1 + x^2} = \frac{1}{1 + 0} = 1 \] \[ f'_+(0) = \lim_{x \to 0^+} a = a \]Affinché la funzione sia derivabile in \(x = 0\), deve essere:
\[ f'_-(0) = f'_+(0) \] \[ 1 = a \]Quindi la funzione è derivabile in \(x = 0\) se e solo se \(a = 1\).
Conclusione sulla derivabilità:
La funzione è derivabile in tutto \(\mathbb{R}\) se e solo se \(a = 1\) e \(b = -1\).
Con i valori trovati, la funzione diventa:
\[ f(x) = \begin{cases} -1 + \arctan x & \text{se } x < 0 \\[8pt] x - 1 & \text{se } x \geq 0 \end{cases} \]Il grafico di tale funzione è facilmente deducibile da funzioni note:
Affinché il Teorema di Rolle sia applicabile in un intervallo \([a, b]\), deve esistere un intervallo in cui \(f(a) = f(b)\) con \(a < b\).
Osserviamo che la funzione \(f(x)\) è strettamente crescente su tutto \(\mathbb{R}\):
Poiché la derivata è sempre positiva, la funzione è strettamente crescente. Questo significa che per ogni coppia di punti distinti \(a < b\), si ha necessariamente:
\[ f(a) < f(b) \]Conclusione:
Non può esistere un intervallo \([a, b]\) con \(a < b\) in cui \(f(a) = f(b)\).
Pertanto, la funzione non soddisfa il Teorema di Rolle in alcun intervallo del dominio, poiché la terza ipotesi (valori uguali agli estremi) non può mai essere verificata.
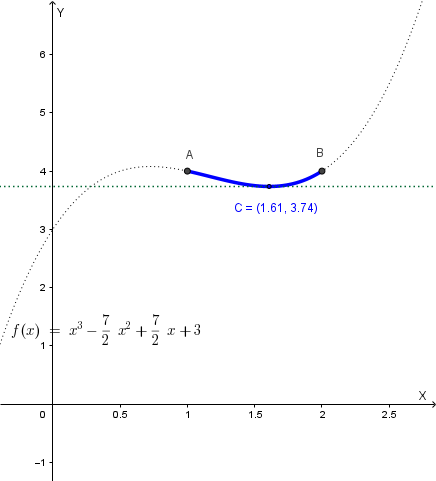
Data la funzione \( y = x^3 + kx^2 - kx + 3 \) nell'intervallo chiuso \([1, 2]\), si determini il valore di \(k\) per il quale sia ad essa applicabile il Teorema di Rolle e si trovi il punto in cui si verifica la tesi del teorema stesso.
Soluzione quesito 7:
La funzione \( f(x) = x^3 + kx^2 - kx + 3 \) è un polinomio (funzione razionale intera), quindi:
Dobbiamo ora determinare per quale valore di \(k\) si ha \(f(1) = f(2)\).
Calcoliamo i valori della funzione agli estremi:
\[ f(1) = 1^3 + k \cdot 1^2 - k \cdot 1 + 3 = 1 + k - k + 3 = 4 \] \[ f(2) = 2^3 + k \cdot 2^2 - k \cdot 2 + 3 = 8 + 4k - 2k + 3 = 11 + 2k \]Imponiamo la condizione \(f(1) = f(2)\):
\[ 4 = 11 + 2k \] \[ 2k = 4 - 11 = -7 \] \[ k = -\frac{7}{2} \]Conclusione:
La funzione soddisfa il Teorema di Rolle se e solo se \( k = -\dfrac{7}{2} \).
Con \( k = -\dfrac{7}{2} \), la funzione diventa:
\[ f(x) = x^3 - \frac{7}{2}x^2 + \frac{7}{2}x + 3 \]Il Teorema di Rolle garantisce l'esistenza di almeno un punto \(c \in (1, 2)\) in cui si annulla la derivata prima.
Calcoliamo la derivata:
\[ f'(x) = 3x^2 - 7x + \frac{7}{2} \]Risolviamo l'equazione \(f'(x) = 0\):
\[ 3x^2 - 7x + \frac{7}{2} = 0 \]Moltiplichiamo per 2 per eliminare la frazione:
\[ 6x^2 - 14x + 7 = 0 \]Applichiamo la formula risolutiva:
\[ x = \frac{14 \pm \sqrt{196 - 168}}{12} = \frac{14 \pm \sqrt{28}}{12} = \frac{14 \pm 2\sqrt{7}}{12} = \frac{7 \pm \sqrt{7}}{6} \]Le due soluzioni sono:
\[ x_1 = \frac{7 - \sqrt{7}}{6} \approx \frac{7 - 2.646}{6} \approx 0.73 \] \[ x_2 = \frac{7 + \sqrt{7}}{6} \approx \frac{7 + 2.646}{6} \approx 1.61 \]Dobbiamo verificare quale delle due soluzioni appartiene all'intervallo \((1, 2)\):
Risultato finale:
Il punto che verifica la tesi del Teorema di Rolle è:
\[ c = \frac{7 + \sqrt{7}}{6} \approx 1.61 \]In questo punto, la derivata si annulla: \(f'(c) = 0\), e la tangente al grafico della funzione è orizzontale.
Dimostrare che se \(p(x)\) è un polinomio, allora tra due qualsiasi radici distinte di \(p(x)\) c'è una radice di \(p'(x)\).
Soluzione quesito 8:
Siano \(a\) e \(b\) due radici distinte di \(p(x)\), con \(a < b\). Questo significa che:
\[ p(a) = 0 \quad \text{e} \quad p(b) = 0 \]Applichiamo il Teorema di Rolle alla funzione \(y = p(x)\) nell'intervallo \([a, b]\).
Verifichiamo le ipotesi:
Poiché tutte le ipotesi del Teorema di Rolle sono soddisfatte, esiste almeno un punto \(c \in (a, b)\) tale che:
\[ p'(c) = 0 \]Abbiamo dimostrato che esiste almeno un punto \(c\) compreso strettamente tra \(a\) e \(b\) in cui la derivata \(p'(x)\) si annulla, cioè \(c\) è una radice di \(p'(x)\).
Tesi dimostrata:
Tra due qualsiasi radici distinte di un polinomio \(p(x)\) esiste almeno una radice della sua derivata \(p'(x)\).
Questo risultato è di fondamentale importanza in analisi matematica e ha diverse conseguenze:
Consideriamo il polinomio \(p(x) = (x-1)(x-3)(x-5) = x^3 - 9x^2 + 23x - 15\).
Le radici di \(p(x)\) sono: \(x = 1, 3, 5\).
La derivata è: \(p'(x) = 3x^2 - 18x + 23\).
Le radici di \(p'(x)\) sono: \(x = \dfrac{18 \pm \sqrt{48}}{6} = 3 \pm \dfrac{\sqrt{12}}{3} \approx 1.85\) e \(4.15\).
Come previsto dal teorema:
