

Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.


Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
Giustificare, con considerazioni analitiche o mediante un'interpretazione grafica, che la seguente equazione:
\[ x^5 + x^3 + 1 = 0 \]ammette una e una sola soluzione reale. Trovare, quindi, l'intervallo \([z; z+1]\) al quale appartiene tale soluzione, essendo \(z\) un numero intero. Determinare poi, utilizzando il metodo di bisezione, un valore approssimato a meno di 0.1 della soluzione.
Soluzione quesito 1:
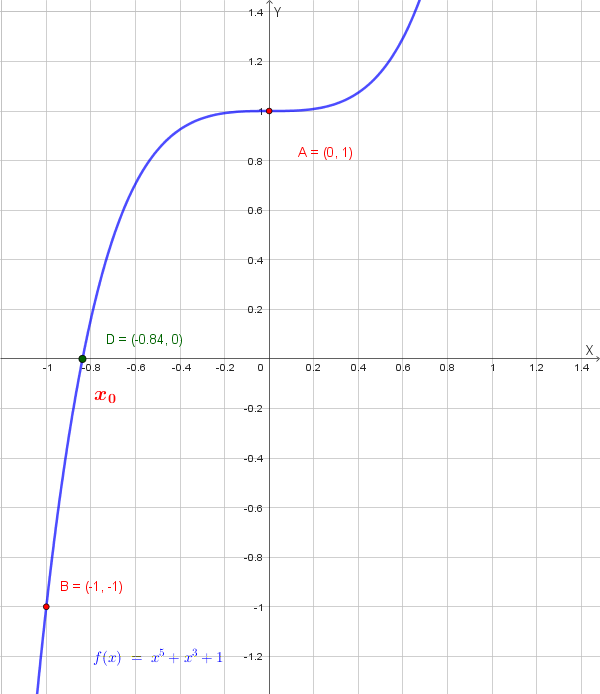
Consideriamo la funzione di equazione \( f(x) = x^5 + x^3 + 1 \). Si tratta di una funzione razionale intera, definita su tutto \(\mathbb{R}\), che tende a \(+\infty\) per \(x \to +\infty\) e a \(-\infty\) per \(x \to -\infty\). Il grafico incontra l'asse \(y\) nel punto di ordinata 1.
La derivata prima è:
\[ f'(x) = 5x^4 + 3x^2 + 1 > 0 \quad \text{per ogni } x \in \mathbb{R} \]La funzione è quindi sempre crescente, pertanto il suo grafico taglia l'asse \(x\) in un solo punto, di ascissa negativa, poiché se \(x = 0\) risulta \(y = 1\).
Siccome \(f(-1) = (-1)^5 + (-1)^3 + 1 = -1 - 1 + 1 = -1 < 0\) e \(f(0) = 1 > 0\), lo zero \(x_0\) della funzione è compreso tra \(-1\) e \(0\).
Conclusione:
L'intervallo a cui appartiene la soluzione dell'equazione è \([-1; 0]\).
Grafico qualitativo della funzione
Applichiamo ora il metodo di bisezione per trovare un valore approssimato della soluzione con errore minore di 0.1.
Partiamo dall'intervallo \([a_0, b_0] = [-1, 0]\) con \(f(a_0) = -1 < 0\) e \(f(b_0) = 1 > 0\).
Iterazione 1:
Punto medio: \(c_1 = \dfrac{-1 + 0}{2} = -0.5\)
\[ f(-0.5) = (-0.5)^5 + (-0.5)^3 + 1 = -0.03125 - 0.125 + 1 = 0.84375 > 0 \]Poiché \(f(c_1) > 0\), lo zero si trova in \([a_1, b_1] = [-1, -0.5]\).
Ampiezza intervallo: \(0.5\)
Iterazione 2:
Punto medio: \(c_2 = \dfrac{-1 + (-0.5)}{2} = -0.75\)
\[ f(-0.75) = (-0.75)^5 + (-0.75)^3 + 1 = -0.2373 - 0.4219 + 1 = 0.3408 > 0 \]Poiché \(f(c_2) > 0\), lo zero si trova in \([a_2, b_2] = [-1, -0.75]\).
Ampiezza intervallo: \(0.25\)
Iterazione 3:
Punto medio: \(c_3 = \dfrac{-1 + (-0.75)}{2} = -0.875\)
\[ f(-0.875) = (-0.875)^5 + (-0.875)^3 + 1 = -0.5130 - 0.6699 + 1 = -0.1829 < 0 \]Poiché \(f(c_3) < 0\), lo zero si trova in \([a_3, b_3] = [-0.875, -0.75]\).
Ampiezza intervallo: \(0.125\)
Iterazione 4:
Punto medio: \(c_4 = \dfrac{-0.875 + (-0.75)}{2} = -0.8125\)
\[ f(-0.8125) = (-0.8125)^5 + (-0.8125)^3 + 1 = -0.3518 - 0.5371 + 1 = 0.1111 > 0 \]Poiché \(f(c_4) > 0\), lo zero si trova in \([a_4, b_4] = [-0.875, -0.8125]\).
Ampiezza intervallo: \(0.0625 < 0.1\)
Conclusione:
Abbiamo ottenuto l'intervallo \([-0.875, -0.8125]\) la cui ampiezza è inferiore a 0.1. Possiamo prendere come valore approssimato della soluzione il punto medio di questo intervallo:
\[ x_0 \approx \frac{-0.875 + (-0.8125)}{2} = -0.84375 \approx -0.84 \]Oppure possiamo scegliere uno qualsiasi dei valori nell'intervallo \([-0.875, -0.8125]\), poiché l'errore è garantito essere minore di 0.1.
La soluzione approssimata (per eccesso) è quindi \( x_0 = -0.8 \)
a) Dimostrare che l'equazione \(\dfrac{1}{x} - e^x = 0\) ha un'unica radice reale utilizzando un metodo grafico e localizzarla fra due interi consecutivi.
b) Calcolare un valore approssimato con due cifre decimali esatte utilizzando il Metodo di Newton dopo aver scelto un opportuno intervallo a cui appartiene la radice richiesta e verificate le condizioni di applicabilità. Motivare la scelta del punto iniziale dell'iterazione della formula di Newton.
Soluzione quesito 2:
Posto \(a(x) = \dfrac{1}{x}\) e \(b(x) = e^x\), le soluzioni dell'equazione data corrispondono alle ascisse dei punti di intersezione dei grafici delle due funzioni.
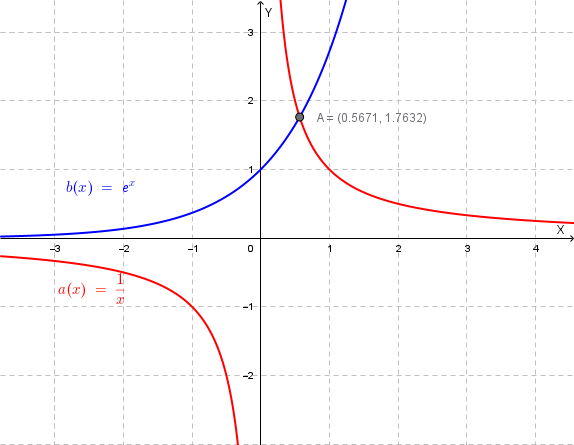
Dal grafico si evince che la radice richiesta è unica e che è compresa tra 0 e 1.
Restringimento dell'intervallo:
Posto \(f(x) = \dfrac{1}{x} - e^x\), calcoliamo i valori della funzione in alcuni punti:
\[ f(0.5) = \frac{1}{0.5} - e^{0.5} = 2 - 1.6487 = 0.3513 > 0 \] \[ f(0.6) = \frac{1}{0.6} - e^{0.6} = 1.6667 - 1.8221 = -0.1554 < 0 \]Quindi la radice appartiene all'intervallo \([0.5, 0.6]\).
Enunciato del Metodo di Newton:
Il Metodo di Newton (o delle tangenti) è un metodo iterativo per approssimare le radici di un'equazione \(f(x) = 0\). Data un'approssimazione iniziale \(x_0\), si calcola la successione:
\[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \]Sotto opportune condizioni, la successione converge alla radice cercata.
Verifica delle condizioni di applicabilità:
Calcoliamo la derivata prima:
\[ f'(x) = -\frac{1}{x^2} - e^x < 0 \quad \text{per ogni } x \neq 0 \]La funzione è sempre decrescente (con \(x \neq 0\)).
Calcoliamo la derivata seconda:
\[ f''(x) = \frac{d}{dx}\left(-\frac{1}{x^2} - e^x\right) = \frac{2}{x^3} - e^x \]Per applicare il Metodo di Newton dobbiamo verificare che la derivata seconda abbia segno costante nell'intervallo a cui appartiene la radice.
\(f''(x) > 0\) se \(\dfrac{2}{x^3} - e^x > 0\), cioè se \(\dfrac{2}{x^3} > e^x\).
Confrontiamo graficamente \(c(x) = \dfrac{2}{x^3}\) e \(d(x) = e^x\):
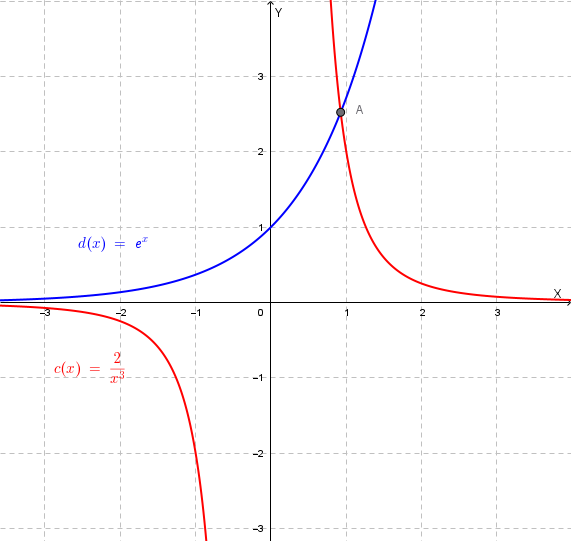
Dal grafico si osserva che le due curve si intersecano in un punto di ascissa circa 1 e che \(\dfrac{2}{x^3} < e^x\) in \([0.5, 0.6]\), quindi in tale intervallo \(f''(x) < 0\), cioè ha segno costante.
Inoltre, \(f''(x)\) ha lo stesso segno di \(f(b) = f(0.6) < 0\). Quindi il punto iniziale dell'iterazione è \(x_0 = b = 0.6\).
Applicazione della formula iterativa:
Utilizziamo la formula:
\[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} = x_n - \frac{\frac{1}{x_n} - e^{x_n}}{-\frac{1}{x_n^2} - e^{x_n}} \]Iterazione 1:
\(x_0 = 0.6\)
\[ f(0.6) = \frac{1}{0.6} - e^{0.6} = 1.6667 - 1.8221 = -0.1554 \] \[ f'(0.6) = -\frac{1}{0.6^2} - e^{0.6} = -2.7778 - 1.8221 = -4.5999 \] \[ x_1 = 0.6 - \frac{-0.1554}{-4.5999} = 0.6 - 0.0338 = 0.5662 \]Iterazione 2:
\(x_1 = 0.5662\)
\[ f(0.5662) = \frac{1}{0.5662} - e^{0.5662} = 1.7662 - 1.7614 = 0.0048 \] \[ f'(0.5662) = -\frac{1}{0.5662^2} - e^{0.5662} = -3.1191 - 1.7614 = -4.8805 \] \[ x_2 = 0.5662 - \frac{0.0048}{-4.8805} = 0.5662 + 0.0010 = 0.5672 \]Iterazione 3:
\(x_2 = 0.5672\)
\[ f(0.5672) = \frac{1}{0.5672} - e^{0.5672} = 1.7630 - 1.7632 = -0.0002 \] \[ f'(0.5672) = -\frac{1}{0.5672^2} - e^{0.5672} = -3.1070 - 1.7632 = -4.8702 \] \[ x_3 = 0.5672 - \frac{-0.0002}{-4.8702} = 0.5672 - 0.00004 = 0.5672 \]Poiché \(x_2\) e \(x_3\) differiscono per meno di un centesimo (anzi, sono praticamente uguali a due cifre decimali), possiamo fermarci.
La soluzione approssimata con due cifre decimali esatte è \( x = 0.56 \)
Dimostrare che l'equazione:
\[ \arctan(x) + x^3 + e^x = 0 \]ha una e una sola soluzione reale. Localizzare la soluzione fra due numeri interi consecutivi e trovare un valore approssimato a meno di 0.1 della soluzione utilizzando il metodo di bisezione.
Soluzione quesito 3:
La funzione \(f(x) = \arctan(x) + x^3 + e^x\) è continua su tutto \(\mathbb{R}\) ed ha i seguenti limiti alla frontiera:
\[ \lim_{x \to -\infty} f(x) = -\frac{\pi}{2} - \infty + 0 = -\infty \] \[ \lim_{x \to +\infty} f(x) = \frac{\pi}{2} + \infty + \infty = +\infty \]Quindi la funzione ammette almeno uno zero.
Studiamo la derivata prima:
\[ f'(x) = \frac{1}{1 + x^2} + 3x^2 + e^x > 0 \quad \text{per ogni } x \in \mathbb{R} \]La funzione è quindi sempre crescente, perciò il suo grafico taglia l'asse delle \(x\) solo una volta; pertanto l'equazione data ammette una sola soluzione reale.
Valutiamo alcuni valori della funzione:
\[ f(0) = \arctan(0) + 0^3 + e^0 = 0 + 0 + 1 = 1 > 0 \] \[ f(-1) = \arctan(-1) + (-1)^3 + e^{-1} = -\frac{\pi}{4} - 1 + \frac{1}{e} \approx -0.7854 - 1 + 0.3679 = -1.4175 < 0 \]Quindi la soluzione appartiene all'intervallo \([a, b] = [-1, 0]\).
Applichiamo il metodo di bisezione per trovare un valore approssimato con errore minore di 0.1.
Partiamo dall'intervallo \([a_0, b_0] = [-1, 0]\) con \(f(a_0) = -1.4175 < 0\) e \(f(b_0) = 1 > 0\).
Iterazione 1:
Punto medio: \(c_1 = \dfrac{-1 + 0}{2} = -0.5\)
\[ f(-0.5) = \arctan(-0.5) + (-0.5)^3 + e^{-0.5} \approx -0.4636 - 0.125 + 0.6065 = 0.0179 > 0 \]Poiché \(f(c_1) > 0\), lo zero si trova in \([a_1, b_1] = [-1, -0.5]\).
Ampiezza intervallo: \(0.5\)
Iterazione 2:
Punto medio: \(c_2 = \dfrac{-1 + (-0.5)}{2} = -0.75\)
\[ f(-0.75) = \arctan(-0.75) + (-0.75)^3 + e^{-0.75} \approx -0.6435 - 0.4219 + 0.4724 = -0.5930 < 0 \]Poiché \(f(c_2) < 0\), lo zero si trova in \([a_2, b_2] = [-0.75, -0.5]\).
Ampiezza intervallo: \(0.25\)
Iterazione 3:
Punto medio: \(c_3 = \dfrac{-0.75 + (-0.5)}{2} = -0.625\)
\[ f(-0.625) = \arctan(-0.625) + (-0.625)^3 + e^{-0.625} \approx -0.5585 - 0.2441 + 0.5353 = -0.2673 < 0 \]Poiché \(f(c_3) < 0\), lo zero si trova in \([a_3, b_3] = [-0.625, -0.5]\).
Ampiezza intervallo: \(0.125\)
Iterazione 4:
Punto medio: \(c_4 = \dfrac{-0.625 + (-0.5)}{2} = -0.5625\)
\[ f(-0.5625) = \arctan(-0.5625) + (-0.5625)^3 + e^{-0.5625} \approx -0.5115 - 0.1780 + 0.5697 = -0.1198 < 0 \]Poiché \(f(c_4) < 0\), lo zero si trova in \([a_4, b_4] = [-0.5625, -0.5]\).
Ampiezza intervallo: \(0.0625 < 0.1\)
Conclusione:
Abbiamo ottenuto l'intervallo \([-0.5625, -0.5]\) la cui ampiezza è inferiore a 0.1. Possiamo prendere come valore approssimato della soluzione un valore in questo intervallo.
La soluzione approssimata (per eccesso) è quindi \( x_0 = -0.5 \)
Si consideri l'equazione:
\[ \ln|x| - e^x = 0 \]Si dimostri che essa ammette una soluzione reale appartenente all'intervallo \(-2 \leq x \leq -1\) e se ne calcoli un valore approssimato con due cifre decimali esatte utilizzando sia il metodo di bisezione sia quello delle tangenti.
Soluzione quesito 4:
L'equazione può essere vista nella forma: \(\ln|x| = e^x\).
Confrontiamo graficamente le due funzioni \(y = \ln|x|\) e \(y = e^x\).
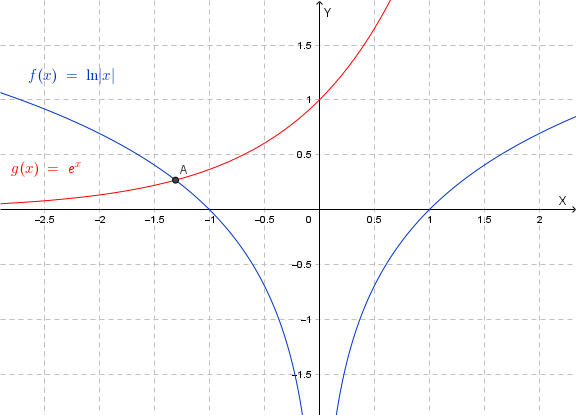
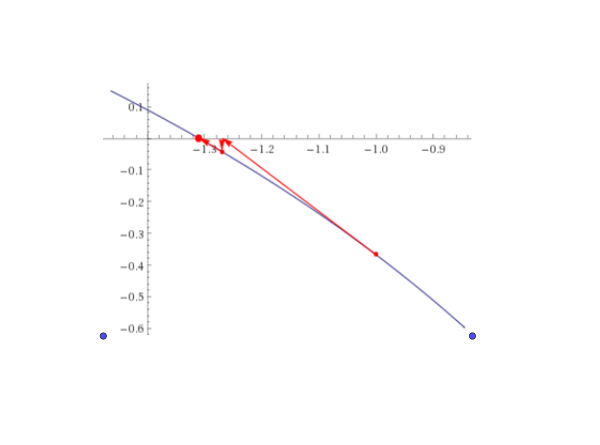
Dal confronto grafico segue chiaramente che l'equazione ammette una ed una sola soluzione tra \(-2\) e \(-1\). Cerchiamo un valore approssimato con due cifre decimali esatte della soluzione.
Utilizziamo il metodo di bisezione nell'intervallo \([a, b] = [-2, -1]\).
Posto \(f(x) = \ln|x| - e^x\), verifichiamo:
\[ f(-2) = \ln(2) - e^{-2} = 0.6931 - 0.1353 = 0.5578 > 0 \] \[ f(-1) = \ln(1) - e^{-1} = 0 - 0.3679 = -0.3679 < 0 \]Iterazione 1:
Punto medio: \(c_1 = \dfrac{-2 + (-1)}{2} = -1.5\)
\[ f(-1.5) = \ln(1.5) - e^{-1.5} = 0.4055 - 0.2231 = 0.1824 > 0 \]Nuovo intervallo: \([-1.5, -1]\), ampiezza: \(0.5\)
Iterazione 2:
Punto medio: \(c_2 = \dfrac{-1.5 + (-1)}{2} = -1.25\)
\[ f(-1.25) = \ln(1.25) - e^{-1.25} = 0.2231 - 0.2865 = -0.0634 < 0 \]Nuovo intervallo: \([-1.5, -1.25]\), ampiezza: \(0.25\)
Iterazione 3:
Punto medio: \(c_3 = \dfrac{-1.5 + (-1.25)}{2} = -1.375\)
\[ f(-1.375) = \ln(1.375) - e^{-1.375} = 0.3185 - 0.2528 = 0.0657 > 0 \]Nuovo intervallo: \([-1.375, -1.25]\), ampiezza: \(0.125\)
Iterazione 4:
Punto medio: \(c_4 = \dfrac{-1.375 + (-1.25)}{2} = -1.3125\)
\[ f(-1.3125) = \ln(1.3125) - e^{-1.3125} = 0.2719 - 0.2693 = 0.0026 > 0 \]Nuovo intervallo: \([-1.3125, -1.25]\), ampiezza: \(0.0625\)
Iterazione 5:
Punto medio: \(c_5 = \dfrac{-1.3125 + (-1.25)}{2} = -1.28125\)
\[ f(-1.28125) = \ln(1.28125) - e^{-1.28125} = 0.2477 - 0.2777 = -0.0300 < 0 \]Nuovo intervallo: \([-1.3125, -1.28125]\), ampiezza: \(0.03125\)
Iterazione 6:
Punto medio: \(c_6 = \dfrac{-1.3125 + (-1.28125)}{2} = -1.296875\)
\[ f(-1.296875) = \ln(1.296875) - e^{-1.296875} = 0.2597 - 0.2734 = -0.0137 < 0 \]Nuovo intervallo: \([-1.3125, -1.296875]\), ampiezza: \(0.015625\)
Iterazione 7:
Punto medio: \(c_7 = \dfrac{-1.3125 + (-1.296875)}{2} = -1.3046875\)
\[ f(-1.3046875) = \ln(1.3046875) - e^{-1.3046875} = 0.2658 - 0.2713 = -0.0055 < 0 \]Nuovo intervallo: \([-1.3125, -1.3046875]\), ampiezza: \(0.0078125\)
Iterazione 8:
Punto medio: \(c_8 = \dfrac{-1.3125 + (-1.3046875)}{2} = -1.30859375\)
\[ f(-1.30859375) = \ln(1.30859375) - e^{-1.30859375} = 0.2688 - 0.2703 = -0.0015 < 0 \]Nuovo intervallo: \([-1.3125, -1.30859375]\), ampiezza: \(0.00390625 < 0.01\)
Con 8 iterazioni abbiamo ottenuto un intervallo di ampiezza inferiore a 0.01, garantendo due cifre decimali esatte.
Soluzione con il metodo di bisezione: \( x \approx -1.31 \)
Usando il metodo delle tangenti, sono sufficienti 3 iterazioni per arrivare alla precisione richiesta.
Verifica delle condizioni:
\[ f(a) = f(-2) = \ln(2) - e^{-2} = 0.5578 > 0 \] \[ f(b) = f(-1) = 0 - e^{-1} = -0.3679 < 0 \]Calcoliamo le derivate:
\[ f'(x) = \frac{1}{x} - e^x \] \[ f''(x) = -\frac{1}{x^2} - e^x < 0 \quad \text{in } [a, b] = [-2, -1] \]Essendo \(f(a) \cdot f''(x) = 0.5578 \cdot (\text{negativo}) < 0\) in \([a, b] = [-2, -1]\), dobbiamo assumere come punto iniziale di iterazione \(x_0 = b = -1\).
Iterazione 1:
\(x_0 = -1\)
\[ f(-1) = 0 - e^{-1} = -0.3679 \] \[ f'(-1) = \frac{1}{-1} - e^{-1} = -1 - 0.3679 = -1.3679 \] \[ x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} = -1 - \frac{-0.3679}{-1.3679} = -1 - 0.2689 = -1.2689 \]Iterazione 2:
\(x_1 = -1.2689\)
\[ f(-1.2689) = \ln(1.2689) - e^{-1.2689} = 0.2380 - 0.2809 = -0.0429 \] \[ f'(-1.2689) = \frac{1}{-1.2689} - e^{-1.2689} = -0.7881 - 0.2809 = -1.0690 \] \[ x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} = -1.2689 - \frac{-0.0429}{-1.0690} = -1.2689 - 0.0401 = -1.3090 \]Iterazione 3:
\(x_2 = -1.3090\)
\[ f(-1.3090) = \ln(1.3090) - e^{-1.3090} = 0.2691 - 0.2701 = -0.0010 \] \[ f'(-1.3090) = \frac{1}{-1.3090} - e^{-1.3090} = -0.7639 - 0.2701 = -1.0340 \] \[ x_3 = x_2 - \frac{f(x_2)}{f'(x_2)} = -1.3090 - \frac{-0.0010}{-1.0340} = -1.3090 - 0.0010 = -1.3100 \]I valori \(x_2 = -1.309\) e \(x_3 = -1.310\) sono uguali con due cifre decimali.
Soluzione con il metodo di Newton: \( x \approx -1.31 \)
Si consideri la funzione di equazione \(f(x) = \dfrac{\pi}{2} \cos(\pi x) + 1\).
a) Dimostrare che la funzione ha periodo \(T = 2\) e rappresentarla graficamente nell'intervallo \([0; 2]\), deducendo il grafico da funzioni elementari con opportune trasformazioni geometriche.
b) Dimostrare che nell'intervallo \(\left[\dfrac{1}{2}, 1\right]\) la funzione si annulla una ed una sola volta.
c) Detto \(c\) lo zero della funzione nell'intervallo \(\left[\dfrac{1}{2}, 1\right]\), trovare un valore approssimato a meno di un decimo utilizzando prima il metodo di bisezione e poi quello della tangente.
Soluzione quesito 5:
Dimostrazione del periodo:
Per dimostrare che il periodo è \(T = 2\), verifichiamo che \(f(x + 2) = f(x)\) per ogni \(x\):
\[ f(x + 2) = \frac{\pi}{2} \cos(\pi(x + 2)) + 1 = \frac{\pi}{2} \cos(\pi x + 2\pi) + 1 \]Poiché \(\cos(\alpha + 2\pi) = \cos(\alpha)\), si ha:
\[ f(x + 2) = \frac{\pi}{2} \cos(\pi x) + 1 = f(x) \]Quindi la funzione ha periodo \(T = 2\).
Costruzione del grafico per trasformazioni geometriche:
Il grafico della funzione \(f(x) = \dfrac{\pi}{2} \cos(\pi x) + 1\) si ottiene dal grafico della funzione coseno mediante le seguenti trasformazioni:
Passo 1: Grafico di \(a(x) = \cos(\pi x)\)
Funzione coseno con periodo \(T = \dfrac{2\pi}{\pi} = 2\) (compressione orizzontale del coseno standard).
Passo 2: Grafico di \(b(x) = \dfrac{\pi}{2} \cos(\pi x)\)
Dilatazione verticale di \(a(x)\) con fattore \(\dfrac{\pi}{2} \approx 1.57\). L'ampiezza delle oscillazioni passa da 1 a \(\dfrac{\pi}{2}\).
Passo 3: Grafico di \(f(x) = \dfrac{\pi}{2} \cos(\pi x) + 1\)
Traslazione verso l'alto di \(b(x)\) mediante il vettore \(\vec{v} = (0, 1)\). L'asse di oscillazione si sposta da \(y = 0\) a \(y = 1\).
Il grafico con i vari passaggi:
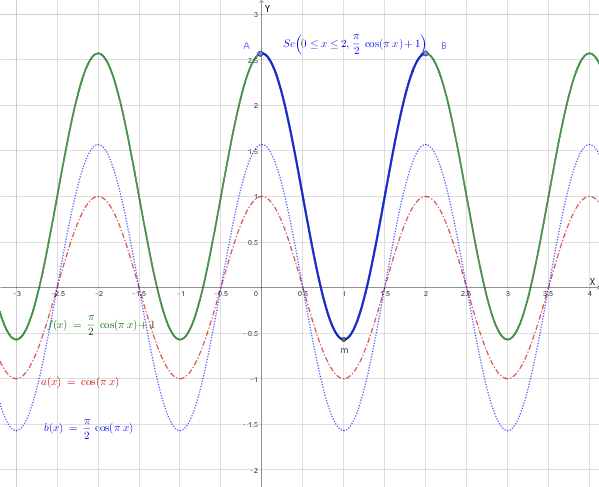
Il grafico finale è il seguente:
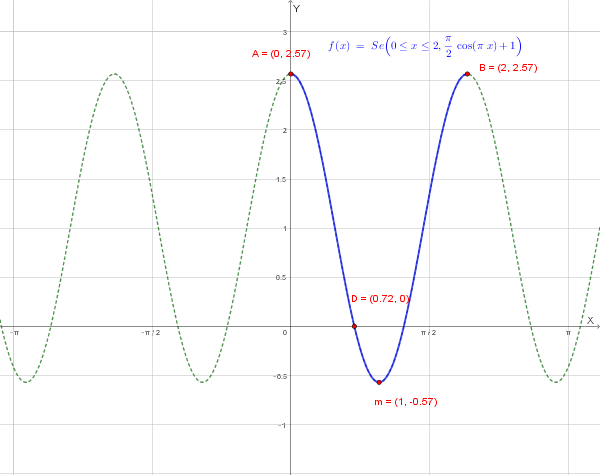
Caratteristiche del grafico:
Dal grafico si osserva che la funzione \(f(x)\) è continua e derivabile su tutto \(\mathbb{R}\).
Valutiamo la funzione agli estremi dell'intervallo:
\[ f\left(\frac{1}{2}\right) = \frac{\pi}{2} \cos\left(\frac{\pi}{2}\right) + 1 = \frac{\pi}{2} \cdot 0 + 1 = 1 > 0 \] \[ f(1) = \frac{\pi}{2} \cos(\pi) + 1 = \frac{\pi}{2} \cdot (-1) + 1 = 1 - \frac{\pi}{2} \approx 1 - 1.57 = -0.57 < 0 \]Poiché \(f\left(\dfrac{1}{2}\right) > 0\) e \(f(1) < 0\), per il teorema degli zeri esiste almeno un valore \(c \in \left(\dfrac{1}{2}, 1\right)\) tale che \(f(c) = 0\).
Per verificare l'unicità, studiamo la derivata prima:
\[ f'(x) = \frac{\pi}{2} \cdot (-\sin(\pi x)) \cdot \pi = -\frac{\pi^2}{2} \sin(\pi x) \]Nell'intervallo \(\left[\dfrac{1}{2}, 1\right]\), si ha \(\pi x \in \left[\dfrac{\pi}{2}, \pi\right]\), quindi \(\sin(\pi x) > 0\). Di conseguenza:
\[ f'(x) = -\frac{\pi^2}{2} \sin(\pi x) < 0 \quad \text{per ogni } x \in \left[\frac{1}{2}, 1\right] \]La funzione è strettamente decrescente nell'intervallo \(\left[\dfrac{1}{2}, 1\right]\), quindi può attraversare l'asse \(x\) una sola volta.
Conclusione: La funzione si annulla una ed una sola volta nell'intervallo \(\left[\dfrac{1}{2}, 1\right]\).
Applichiamo il metodo di bisezione nell'intervallo \(\left[a, b\right] = \left[\dfrac{1}{2}, 1\right]\).
Iterazione 1:
Punto medio: \(c_1 = \dfrac{0.5 + 1}{2} = 0.75\)
\[ f(0.75) = \frac{\pi}{2} \cos(0.75\pi) + 1 = \frac{\pi}{2} \cdot (-0.7071) + 1 \approx -1.1107 + 1 = -0.1107 < 0 \]Nuovo intervallo: \([0.5, 0.75]\), ampiezza: \(0.25\)
Iterazione 2:
Punto medio: \(c_2 = \dfrac{0.5 + 0.75}{2} = 0.625\)
\[ f(0.625) = \frac{\pi}{2} \cos(0.625\pi) + 1 = \frac{\pi}{2} \cdot (-0.3827) + 1 \approx -0.6011 + 1 = 0.3989 > 0 \]Nuovo intervallo: \([0.625, 0.75]\), ampiezza: \(0.125\)
Iterazione 3:
Punto medio: \(c_3 = \dfrac{0.625 + 0.75}{2} = 0.6875\)
\[ f(0.6875) = \frac{\pi}{2} \cos(0.6875\pi) + 1 = \frac{\pi}{2} \cdot (-0.5556) + 1 \approx -0.8727 + 1 = 0.1273 > 0 \]Nuovo intervallo: \([0.6875, 0.75]\), ampiezza: \(0.0625 < 0.1\)
Abbiamo ottenuto un intervallo di ampiezza inferiore a 0.1.
Soluzione con il metodo di bisezione: \( c \approx 0.7 \) (per difetto)
Verifica delle condizioni di applicabilità:
Calcoliamo la derivata seconda:
\[ f''(x) = -\frac{\pi^2}{2} \cdot \cos(\pi x) \cdot \pi = -\frac{\pi^3}{2} \cos(\pi x) \]Nell'intervallo \(\left[\dfrac{1}{2}, 1\right]\), si ha \(\pi x \in \left[\dfrac{\pi}{2}, \pi\right]\), quindi \(\cos(\pi x) < 0\). Di conseguenza:
\[ f''(x) = -\frac{\pi^3}{2} \cos(\pi x) > 0 \quad \text{per ogni } x \in \left[\frac{1}{2}, 1\right] \]La derivata seconda ha segno costante (positivo) nell'intervallo. Verifichiamo il segno di \(f(a) \cdot f''(x)\):
\[ f\left(\frac{1}{2}\right) \cdot f''(x) = 1 \cdot (\text{positivo}) > 0 \]Poiché \(f(a) \cdot f''(x) > 0\), il punto iniziale dell'iterazione è \(x_0 = a = 0.5\).
Iterazione 1:
\(x_0 = 0.5\)
\[ f(0.5) = 1 \] \[ f'(0.5) = -\frac{\pi^2}{2} \sin\left(\frac{\pi}{2}\right) = -\frac{\pi^2}{2} \cdot 1 = -\frac{\pi^2}{2} \approx -4.9348 \] \[ x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} = 0.5 - \frac{1}{-4.9348} = 0.5 + 0.2026 = 0.7026 \]Iterazione 2:
\(x_1 = 0.7026\)
\[ f(0.7026) = \frac{\pi}{2} \cos(0.7026\pi) + 1 \approx \frac{\pi}{2} \cdot (-0.6157) + 1 \approx -0.9676 + 1 = 0.0324 \] \[ f'(0.7026) = -\frac{\pi^2}{2} \sin(0.7026\pi) \approx -\frac{\pi^2}{2} \cdot 0.7880 \approx -3.8886 \] \[ x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} = 0.7026 - \frac{0.0324}{-3.8886} = 0.7026 + 0.0083 = 0.7109 \]Iterazione 3:
\(x_2 = 0.7109\)
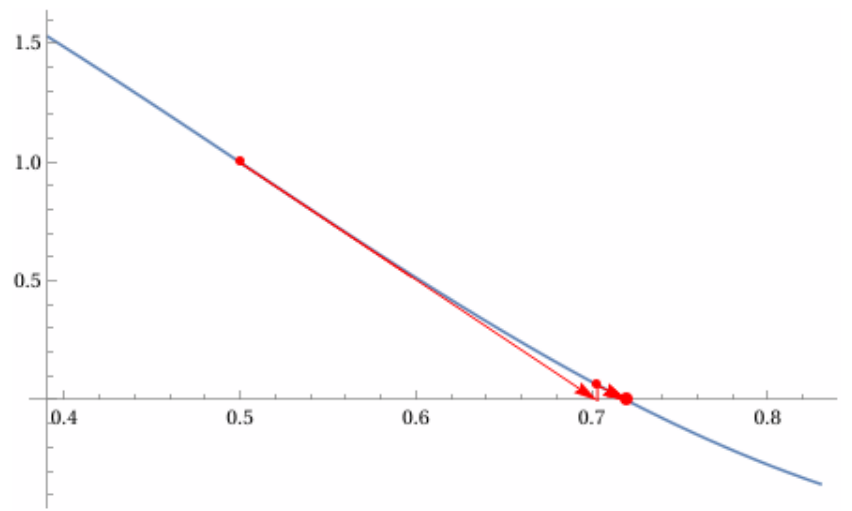
\[ f(0.7109) = \frac{\pi}{2} \cos(0.7109\pi) + 1 \approx \frac{\pi}{2} \cdot (-0.6403) + 1 \approx -1.0062 + 1 = -0.0062 \] \[ f'(0.7109) = -\frac{\pi^2}{2} \sin(0.7109\pi) \approx -\frac{\pi^2}{2} \cdot 0.7682 \approx -3.7911 \] \[ x_3 = x_2 - \frac{f(x_2)}{f'(x_2)} = 0.7109 - \frac{-0.0062}{-3.7911} = 0.7109 - 0.0016 = 0.7093 \]I valori \(x_2 = 0.7109\) e \(x_3 = 0.7093\) sono molto vicini. Arrotondando a un decimale, entrambi danno \(0.7\).
Soluzione con il metodo di Newton: \( c \approx 0.7 \)
Si consideri la funzione \(g(x) = a \cdot 2^x + b \cdot 2^{-x}\).
a) Determinare \(a\) e \(b\) sapendo che la funzione è pari e che il suo grafico passa per il punto \(A = (0, 2)\).
b) Studiare la funzione e rappresentarla graficamente.
c) Considerata la retta \(r\) di equazione \(y = 4\), determinare il valore approssimato a meno di un decimo dell'ascissa \(\alpha\) del punto di intersezione \(B\) appartenente al primo quadrante (utilizzare prima il metodo di bisezione e poi quello delle tangenti).
Soluzione quesito 6:
Condizione 1 - Funzione pari:
Una funzione è pari se \(g(-x) = g(x)\) per ogni \(x\) del dominio.
\[ g(-x) = a \cdot 2^{-x} + b \cdot 2^x \]Imponendo \(g(-x) = g(x)\):
\[ a \cdot 2^{-x} + b \cdot 2^x = a \cdot 2^x + b \cdot 2^{-x} \] \[ (a - b) \cdot 2^{-x} = (a - b) \cdot 2^x \]Questa uguaglianza deve valere per ogni \(x\), quindi:
\[ a - b = 0 \quad \Rightarrow \quad a = b \]Condizione 2 - Passaggio per A(0, 2):
Imponiamo \(g(0) = 2\):
\[ g(0) = a \cdot 2^0 + b \cdot 2^0 = a + b = 2 \]Poiché \(a = b\), si ha:
\[ a + a = 2 \quad \Rightarrow \quad 2a = 2 \quad \Rightarrow \quad a = 1 \]Quindi \(b = 1\).
La funzione richiesta è: \(g(x) = 2^x + 2^{-x}\)
Dominio:
La funzione è definita per ogni \(x \in \mathbb{R}\).
\[ D = \mathbb{R} \]Intersezioni con gli assi:
Con l'asse \(y\): \(g(0) = 2^0 + 2^0 = 1 + 1 = 2\). Punto: \((0, 2)\).
Con l'asse \(x\): \(g(x) = 0 \Rightarrow 2^x + 2^{-x} = 0\). Poiché \(2^x > 0\) e \(2^{-x} > 0\) per ogni \(x\), la somma è sempre positiva. Nessuna intersezione con l'asse \(x\).
Segno:
\(g(x) = 2^x + 2^{-x} > 0\) per ogni \(x \in \mathbb{R}\).
Limiti alla frontiera:
\[ \lim_{x \to +\infty} g(x) = \lim_{x \to +\infty} (2^x + 2^{-x}) = +\infty + 0 = +\infty \] \[ \lim_{x \to -\infty} g(x) = \lim_{x \to -\infty} (2^x + 2^{-x}) = 0 + \infty = +\infty \]Non ci sono asintoti orizzontali né verticali.
Monotonia - Derivata prima:
\[ g'(x) = 2^x \ln(2) - 2^{-x} \ln(2) = \ln(2) \cdot (2^x - 2^{-x}) \]Studiamo il segno di \(g'(x)\):
\[ g'(x) = 0 \quad \Rightarrow \quad 2^x - 2^{-x} = 0 \quad \Rightarrow \quad 2^x = 2^{-x} \quad \Rightarrow \quad 2^{2x} = 1 \quad \Rightarrow \quad x = 0 \]Per \(x < 0\): \(2^x < 1\) e \(2^{-x} > 1\), quindi \(2^x - 2^{-x} < 0\) e \(g'(x) < 0\) (funzione decrescente).
Per \(x > 0\): \(2^x > 1\) e \(2^{-x} < 1\), quindi \(2^x - 2^{-x} > 0\) e \(g'(x) > 0\) (funzione crescente).
In \(x = 0\) la funzione ha un minimo assoluto: \(g(0) = 2\).
Concavità - Derivata seconda:
\[ g''(x) = \ln(2) \cdot (2^x \ln(2) + 2^{-x} \ln(2)) = (\ln(2))^2 \cdot (2^x + 2^{-x}) > 0 \]La derivata seconda è sempre positiva, quindi la funzione è concava verso l'alto su tutto \(\mathbb{R}\). Non ci sono punti di flesso.
Grafico della funzione:
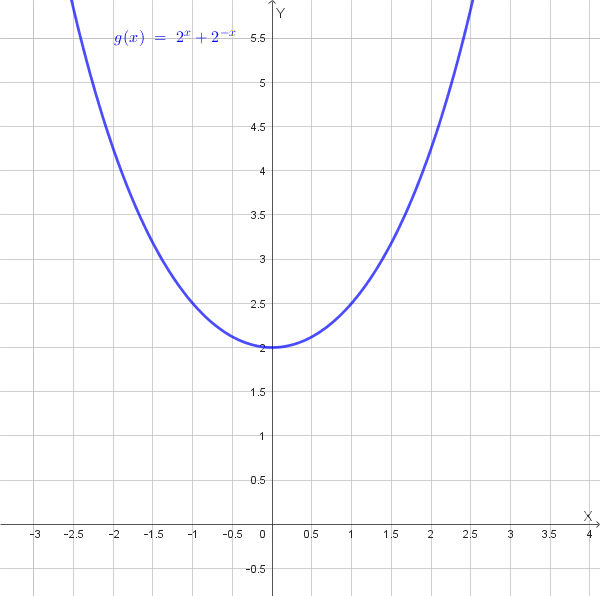
Rappresentiamo nello stesso piano cartesiano il grafico \(G\) di \(g\) e la retta \(r: y = 4\).
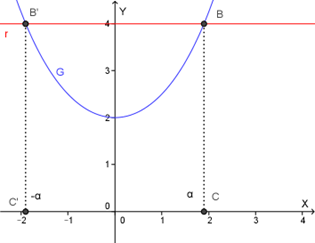
L'ascissa \(\alpha\) dell'intersezione \(B\) del primo quadrante è compresa fra 1 e 2. Infatti:
\[ g(1) = 2^1 + 2^{-1} = 2 + 0.5 = 2.5 < 4 \] \[ g(2) = 2^2 + 2^{-2} = 4 + 0.25 = 4.25 > 4 \]Quindi per \(x = 1\) la retta \(r\) è al di sopra del grafico \(G\), mentre per \(x = 2\) la retta \(r\) è al di sotto del grafico \(G\).
Le ascisse \(\alpha\) e \(-\alpha\) delle due intersezioni fra \(G\) ed \(r\) si ottengono risolvendo l'equazione:
\[ 2^x + 2^{-x} = 4 \]Equivalente a:
\[ 2^x + 2^{-x} - 4 = 0 \]Dobbiamo trovare la soluzione \(\alpha\) positiva di questa equazione, appartenente all'intervallo \([1, 2]\), approssimandola a meno di un decimo.
Posto \(f(x) = 2^x + 2^{-x} - 4\), applichiamo il metodo di bisezione nell'intervallo \([1, 2]\).
\[ f(1) = 2.5 - 4 = -1.5 < 0 \] \[ f(2) = 4.25 - 4 = 0.25 > 0 \]Iterazione 1:
Punto medio: \(c_1 = \dfrac{1 + 2}{2} = 1.5\)
\[ f(1.5) = 2^{1.5} + 2^{-1.5} - 4 = 2.8284 + 0.3536 - 4 = -0.8180 < 0 \]Nuovo intervallo: \([1.5, 2]\), ampiezza: \(0.5\)
Iterazione 2:
Punto medio: \(c_2 = \dfrac{1.5 + 2}{2} = 1.75\)
\[ f(1.75) = 2^{1.75} + 2^{-1.75} - 4 = 3.3636 + 0.2973 - 4 = -0.3391 < 0 \]Nuovo intervallo: \([1.75, 2]\), ampiezza: \(0.25\)
Iterazione 3:
Punto medio: \(c_3 = \dfrac{1.75 + 2}{2} = 1.875\)
\[ f(1.875) = 2^{1.875} + 2^{-1.875} - 4 = 3.6742 + 0.2722 - 4 = -0.0536 < 0 \]Nuovo intervallo: \([1.875, 2]\), ampiezza: \(0.125\)
Iterazione 4:
Punto medio: \(c_4 = \dfrac{1.875 + 2}{2} = 1.9375\)
\[ f(1.9375) = 2^{1.9375} + 2^{-1.9375} - 4 = 3.8340 + 0.2609 - 4 = 0.0949 > 0 \]Nuovo intervallo: \([1.875, 1.9375]\), ampiezza: \(0.0625 < 0.1\)
Abbiamo ottenuto un intervallo di ampiezza inferiore a 0.1.
Soluzione con il metodo di bisezione: \( \alpha \approx 1.9 \) (per difetto)
![Grafico di f(x) nell'intervallo [1,2]](questionario-6f.png)
Verifica delle condizioni di applicabilità:
Calcoliamo le derivate:
\[ f'(x) = 2^x \ln(2) - 2^{-x} \ln(2) \] \[ f''(x) = (\ln(2))^2 \cdot (2^x + 2^{-x}) > 0 \quad \text{per ogni } x \in [1, 2] \]La derivata seconda è sempre positiva nell'intervallo \([1, 2]\).
Verifichiamo il segno di \(f(a) \cdot f''(x)\):
\[ f(1) \cdot f''(x) = (-1.5) \cdot (\text{positivo}) < 0 \] \[ f(2) \cdot f''(x) = (0.25) \cdot (\text{positivo}) > 0 \]Poiché \(f(2) \cdot f''(x) > 0\), il punto iniziale dell'iterazione è \(x_0 = 2\).
Iterazione 1:
\(x_0 = 2\)
\[ f(2) = 0.25 \] \[ f'(2) = 2^2 \ln(2) - 2^{-2} \ln(2) = 4 \cdot 0.6931 - 0.25 \cdot 0.6931 = 2.7726 - 0.1733 = 2.5993 \] \[ x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} = 2 - \frac{0.25}{2.5993} = 2 - 0.0962 = 1.9038 \]Iterazione 2:
\(x_1 = 1.9038\)
\[ f(1.9038) = 2^{1.9038} + 2^{-1.9038} - 4 = 3.7433 + 0.2672 - 4 = 0.0105 \] \[ f'(1.9038) = 2^{1.9038} \ln(2) - 2^{-1.9038} \ln(2) = 2.5952 - 0.1852 = 2.4100 \] \[ x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} = 1.9038 - \frac{0.0105}{2.4100} = 1.9038 - 0.0044 = 1.8994 \]I valori \(x_1 = 1.904\) e \(x_2 = 1.899\) sono molto vicini e arrotondati a un decimale danno entrambi \(1.9\).
Soluzione con il metodo di Newton: \( \alpha \approx 1.9 \)
