Soluzione approssimata di un'equazione

Che cosa significa risolvere un'equazione in modo approssimato?

Quando abbiamo un'equazione del tipo f(x) = 0, spesso non è possibile trovare una soluzione esatta usando metodi algebrici tradizionali. I **metodi numerici** ci permettono di trovare soluzioni approssimate con la precisione desiderata.

Esempio pratico:

L'equazione x³ - x - 1 = 0 non ha una soluzione algebrica semplice, ma possiamo trovare che x ≈ 1.324718 è una soluzione approssimata molto precisa.

Vantaggi dei metodi numerici:

**Universalità:** Funzionano con qualsiasi tipo di equazione
**Precisione controllabile:** Possiamo scegliere il grado di approssimazione
**Implementazione computerizzata:** Ideali per calcoli automatici

Obiettivo: Trovare x* tale che |f(x*)| < ε
dove ε è la tolleranza desiderata

Come individuare gli intervalli contenenti le radici

Prima di applicare un metodo numerico, dobbiamo **isolare** la radice, cioè trovare un intervallo [a,b] che contiene una e una sola radice.

Teorema degli zeri: Se f(x) è continua in [a,b] e f(a) · f(b) < 0,
allora esiste almeno un punto c ∈ (a,b) tale che f(c) = 0

Esempio: f(x) = x³ - 2x - 5

Passo 1: Valutiamo f(x) in alcuni punti

f(0) = 0³ - 2(0) - 5 = -5
f(1) = 1³ - 2(1) - 5 = -6
f(2) = 2³ - 2(2) - 5 = -1
f(3) = 3³ - 2(3) - 5 = 16

Passo 2: Identifichiamo il cambio di segno

f(2) = -1 < 0 e f(3) = 16 > 0

Quindi f(2) · f(3) < 0 ⇒ esiste una radice in (2,3)

Risultato: La radice è isolata nell'intervallo [2,3]

Strategie per l'isolamento:

**Tabulazione:** Calcolare f(x) per valori equidistanti
**Analisi grafica:** Osservare dove il grafico attraversa l'asse x
**Studio della derivata:** Analizzare crescenza e decrescenza

Risoluzione mediante rappresentazione grafica

Il metodo grafico consiste nel **disegnare il grafico** della funzione f(x) e identificare visivamente i punti dove interseca l'asse delle x.

Procedimento:

1. Tracciare il grafico di y = f(x)

2. Individuare i punti di intersezione con l'asse x

3. Leggere le coordinate x di questi punti

Esempio 1: f(x) = x² - 3

Tracciamo il grafico della parabola y = x² - 3 Grafico di y = x² - 3

Osserviamo che il grafico interseca l'asse x in due punti:

x₁ ≈ -1.7
x₂ ≈ +1.7

Esempio 2: Metodo delle due funzioni

Equazione: ln(x) + x = 0

Trasformazione: Invece di cercare gli zeri di f(x) = ln(x) + x, risolviamo il sistema:

y = ln(x)
y = -x

Interpretazione grafica:

f(x) = ln(x): curva logaritmica (dominio x > 0)
g(x) = -x: retta con pendenza -1
**Soluzione:** punto di intersezione tra le due curve

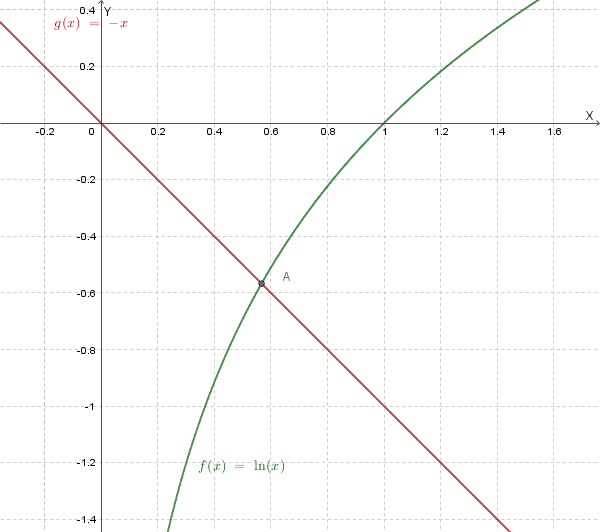Grafico delle due funzioni: Grafico delle funzioni y=ln(x) e y=-x

Risultato: Le due curve si intersecano in un punto con x compreso fra 0.5 e 0.6

**Vantaggio di questo approccio:** Spesso è più facile visualizzare l'intersezione di due curve semplici piuttosto che trovare gli zeri di una funzione complessa.

Vantaggi e svantaggi:

✅ Vantaggi

Intuitivo e visuale
Mostra tutte le radici
Fornisce informazioni qualitative

❌ Svantaggi

Precisione limitata
Dipende dalla scala del grafico
Difficile per funzioni complesse

Il metodo di bisezione (o dicotomico)

È un metodo **robusto e sicuro** che dimezza iterativamente l'intervallo contenente la radice.

Dato [a,b] con f(a) · f(b) < 0:
1. c = (a+b)/2
2. Se f(a) · f(c) < 0 ⇒ nuovo intervallo [a,c]
3. Altrimenti &implies; nuovo intervallo [c,b]

Esempio: f(x) = x³ - x - 1, intervallo [1,2]

Verifica iniziale:
f(1) = 1³ - 1 - 1 = -1 < 0
f(2) = 2³ - 2 - 1 = 5 > 0
f(1) · f(2) < 0 ✓

Iterazione 1:
c₁ = (1+2)/2 = 1.5
f(1.5) = 3.375 - 1.5 - 1 = 0.875 > 0
f(1) · f(1.5) < 0 ⇒ nuovo intervallo [1, 1.5]

Iterazione 2:
c₂ = (1+1.5)/2 = 1.25
f(1.25) ≈ -0.297 < 0
f(1.25) · f(1.5) < 0 ⇒ nuovo intervallo [1.25, 1.5]

Continuando...
Dopo 10 iterazioni: x ≈ 1.3247
Errore < (2-1)/2¹⁰ ≈ 0.001

Caratteristiche del metodo:

**Convergenza garantita:** Sempre converge se f è continua
**Velocità:** Convergenza lineare (lenta ma sicura)
**Errore controllabile:** |errore| ≤ (b-a)/2ⁿ dopo n iterazioni

Il metodo di Newton-Raphson

È un metodo molto **veloce** che utilizza la derivata della funzione per approssimare la radice mediante la tangente.

Formula iterativa: x_n+1 = x_n - f(x_n)/f'(x_n)

Idea geometrica:

Partendo da un punto x₀, tracciamo la tangente al grafico in quel punto. L'intersezione della tangente con l'asse x ci dà la prossima approssimazione x₁.

Esempio: f(x) = x² - 2 (per trovare √2)

Passo 1: Calcoliamo f'(x)
f(x) = x² - 2 ⇒ f'(x) = 2x

Passo 2: Formula iterativa
x_n+1 = x_n - (x_n² - 2)/(2x_n) = (x_n + 2/x_n)/2

Iterazioni:
x₀ = 1 (valore iniziale)
x₁ = (1 + 2/1)/2 = 1.5
x₂ = (1.5 + 2/1.5)/2 ≈ 1.4167
x₃ = (1.4167 + 2/1.4167)/2 ≈ 1.4142
x₄ ≈ 1.41421356... = √2

Vantaggi e requisiti:

✅ Vantaggi

**Convergenza quadratica** (molto veloce)
Poche iterazioni necessarie
Alta precisione

⚠️ Requisiti

f'(x) deve esistere
f'(x) ≠ 0 vicino alla radice
Buona scelta del valore iniziale

Criterio di arresto: |x_n+1 - x_n| < ε oppure |f(x_n)| < ε