Test sulla Soluzione Approssimata di un'Equazione

1. Studiamo qualitativamente la cubica \(y=f(x)=x^3-3x+1\).

La funzione tende a \(\pm\infty\) per \(x\) che tende a \(\pm\infty\).

Taglia l'asse delle \(y\) in \(y=1\).

La sua derivata prima è \(f'(x)=3x^2-3\).

Risulta \(f'(x) > 0\) per \(x < -1\) e per \(x > 1\).

La funzione è quindi crescente se \(x < -1\) e per \(x > 1\), e decrescente per \(-1 < x < 1\).

Quindi \(x=-1\) è punto di massimo relativo, con ordinata \(f(-1) = (-1)^3 - 3(-1) + 1 = -1 + 3 + 1 = 3\).

E \(x=1\) è punto di minimo relativo con ordinata \(f(1) = 1^3 - 3(1) + 1 = 1 - 3 + 1 = -1\).

Il grafico della funzione è quindi del tipo:

Dal grafico si deduce che l'equazione \(x^3-3x+1=0\) ammette tre soluzioni, di cui una compresa fra 0 e 1.

Applichiamo il metodo di bisezione per determinare un valore approssimato a meno di un decimo di questa soluzione:

Iterazione 1:

Intervallo iniziale \([a_0, b_0] = [0, 1]\)

\(f(0) = 1\)

\(f(1) = -1\)

Punto medio \(x_0 = (0+1)/2 = 0.5\)

\(f(0.5) = (0.5)^3 - 3(0.5) + 1 = 0.125 - 1.5 + 1 = -0.375\)

Poiché \(f(0) > 0\) e \(f(0.5) < 0\), la radice è in \([0, 0.5]\).

Nuovo intervallo \([a_1, b_1] = [0, 0.5]\). Lunghezza = 0.5.

Iterazione 2:

Intervallo \([a_1, b_1] = [0, 0.5]\)

Punto medio \(x_1 = (0+0.5)/2 = 0.25\)

\(f(0.25) = (0.25)^3 - 3(0.25) + 1 = 0.015625 - 0.75 + 1 = 0.265625\)

Poiché \(f(0.25) > 0\) e \(f(0.5) < 0\), la radice è in \([0.25, 0.5]\).

Nuovo intervallo \([a_2, b_2] = [0.25, 0.5]\). Lunghezza = 0.25.

Iterazione 3:

Intervallo \([a_2, b_2] = [0.25, 0.5]\)

Punto medio \(x_2 = (0.25+0.5)/2 = 0.375\)

\(f(0.375) = (0.375)^3 - 3(0.375) + 1 = 0.052734375 - 1.125 + 1 = -0.072265625\)

Poiché \(f(0.25) > 0\) e \(f(0.375) < 0\), la radice è in \([0.25, 0.375]\).

Nuovo intervallo \([a_3, b_3] = [0.25, 0.375]\). Lunghezza = 0.125.

Poiché la lunghezza dell'intervallo (0.125) è minore di 0.2 (due volte la precisione richiesta), possiamo fermarci qui.

Il punto medio di questo intervallo è \(x_3 = (0.25+0.375)/2 = 0.3125\).

Il valore approssimato a meno di un decimo è quindi 0.3 (arrotondando 0.3125 alla prima cifra decimale).

L'equazione può essere vista come \(e^x = -3x\). Rappresentiamo nello stesso sistema di riferimento le funzioni \(a(x)=e^x\) e \(b(x)=-3x\).

Risulta:

• \(a(-1) = e^{-1} \approx 0.368\)
• \(b(-1) = -3(-1) = 3\)

Da questi valori, si nota che \(a(-1) < b(-1)\).

• \(a(0) = e^0 = 1\)
• \(b(0) = -3(0) = 0\)

Da questi valori, si nota che \(a(0) > b(0)\).

Dal grafico e dal fatto che \(f(x) = e^x + 3x\) è continua e cambia segno tra -1 e 0 (\(f(-1) = e^{-1} - 3 \approx 0.368 - 3 = -2.632\) e \(f(0) = 1\)), si deduce che esiste almeno una soluzione compresa tra -1 e 0.

Dal grafico precedente si deduce che la soluzione è unica.

Ora applichiamo il metodo di Newton.

Posto \(f(x) = e^x + 3x\), le derivate sono:

\(f'(x) = e^x + 3\)

\(f''(x) = e^x\)

La derivata seconda \(f''(x) = e^x\) ha segno costante (è sempre positiva per ogni \(x\)).

Risulta \(f(0) = 1 > 0\) ed \(f(-1) = e^{-1} - 3 \approx 0.368 - 3 = -2.632 < 0\).

Per il metodo di Newton, dobbiamo scegliere un punto iniziale \(x_0\) tale che \(f(x_0)\) e \(f''(x_0)\) abbiano lo stesso segno. Poiché \(f''(x)\) è sempre positiva, dobbiamo scegliere \(x_0\) tale che \(f(x_0) > 0\). Nell'intervallo \([-1, 0]\), sappiamo che \(f(0) = 1 > 0\). Quindi, il punto iniziale dell'iterazione è \(x_0 = 0\).

La formula iterativa del metodo di Newton è: \(x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\).

Iterazione 0: \(x_0 = 0\)

\(f(x_0) = f(0) = e^0 + 3(0) = 1 + 0 = 1\)

\(f'(x_0) = f'(0) = e^0 + 3 = 1 + 3 = 4\)

\(x_1 = x_0 - \frac{1}{4} = -0.25\)

Iterazione 1: \(x_1 = -0.25\)

\(f(x_1) = f(-0.25) = e^{-0.25} + 3(-0.25) \approx 0.7788 - 0.75 = 0.0288\)

\(f'(x_1) = f'(-0.25) = e^{-0.25} + 3 \approx 0.7788 + 3 = 3.7788\)

\(x_2 = x_1 - \frac{0.0288}{3.7788} \approx -0.25 - 0.00762 = -0.25762\)

Iterazione 2: \(x_2 = -0.25762\)

\(f(x_2) = f(-0.25762) = e^{-0.25762} + 3(-0.25762) \approx 0.77295 - 0.77286 = 0.00009\)

\(f'(x_2) = f'(-0.25762) = e^{-0.25762} + 3 \approx 0.77295 + 3 = 3.77295\)

\(x_3 = x_2 - \frac{0.00009}{3.77295} \approx -0.25762 - 0.00002 = -0.25764\)

Abbiamo raggiunto una precisione sufficiente. Confrontando \(x_2\) e \(x_3\), vediamo che le prime tre cifre decimali sono stabili: \(-0.257\). Il valore approssimato a meno di 1 millesimo è \(-0.257\).

La funzione è \(f(x) = \pi \cos(\pi x) + 2\).

L'equazione da risolvere è \(f(x)=0\), ovvero \(\pi \cos(\pi x) + 2 = 0\).

L'intervallo dato è \([0.5, 1]\). Verifichiamo i segni della funzione agli estremi dell'intervallo:

• \(f(0.5) = \pi \cos(\pi \cdot 0.5) + 2 = \pi \cos(\frac{\pi}{2}) + 2 = \pi(0) + 2 = 2\) (segno positivo)
• \(f(1) = \pi \cos(\pi \cdot 1) + 2 = \pi \cos(\pi) + 2 = \pi(-1) + 2 = 2 - \pi \approx 2 - 3.14159 = -1.14159\) (segno negativo)

Poiché \(f(0.5)\) e \(f(1)\) hanno segni opposti, la radice è compresa nell'intervallo \([0.5, 1]\). Applichiamo il metodo di bisezione per determinare un valore approssimato a meno di 1/10 (cioè, l'errore assoluto deve essere \(\le 0.1\), quindi la lunghezza dell'intervallo finale \(\le 0.2\)).

Iterazione 1:

Intervallo iniziale \([a_0, b_0] = [0.5, 1]\)

\(f(0.5) = 2\)

\(f(1) \approx -1.14159\)

Punto medio \(x_0 = (0.5+1)/2 = 0.75\)

\(f(0.75) = \pi \cos(0.75\pi) + 2 = \pi (-\frac{\sqrt{2}}{2}) + 2 \approx 3.14159(-0.7071) + 2 = -2.2214 + 2 = -0.2214\)

Poiché \(f(0.5) > 0\) e \(f(0.75) < 0\), la radice si trova nell'intervallo \([0.5, 0.75]\).

Nuovo intervallo \([a_1, b_1] = [0.5, 0.75]\). Lunghezza = 0.25.

Iterazione 2:

Intervallo \([a_1, b_1] = [0.5, 0.75]\)

Punto medio \(x_1 = (0.5+0.75)/2 = 0.625\)

\(f(0.625) = \pi \cos(0.625\pi) + 2 \approx 3.14159(-0.38268) + 2 \approx -1.2033 + 2 = 0.7967\)

Poiché \(f(0.625) > 0\) e \(f(0.75) < 0\), la radice si trova nell'intervallo \([0.625, 0.75]\).

Nuovo intervallo \([a_2, b_2] = [0.625, 0.75]\). Lunghezza = 0.125.

La lunghezza dell'intervallo (0.125) è minore di 0.2. Possiamo fermarci qui.

Il punto medio di questo intervallo è \(x_2 = (0.625 + 0.75)/2 = 0.6875\).

Il valore approssimato a meno di un decimo è quindi 0.7 (arrotondando 0.6875 alla prima cifra decimale).

La funzione è \(f(x) = 2\ln(x) - x + 1\). L'intervallo dato è \([0.5, 1]\).

Verifichiamo i segni della funzione agli estremi dell'intervallo:

• \(f(0.5) = 2\ln(0.5) - 0.5 + 1 \approx 2(-0.6931) - 0.5 + 1 = -1.3862 - 0.5 + 1 = -0.8862\) (segno negativo)
• \(f(1) = 2\ln(1) - 1 + 1 = 2(0) - 1 + 1 = 0\) (la radice è esattamente 1! Ma per l'esercizio proseguiamo con il metodo.)

Poiché \(f(0.5) < 0\) e \(f(1) = 0\), la radice è in \([0.5, 1]\).

Applichiamo il metodo di bisezione. La precisione richiesta è un decimo, quindi l'intervallo finale deve avere lunghezza \(\le 0.2\).

Iterazione 1:

Intervallo iniziale \([a_0, b_0] = [0.5, 1]\)

\(f(0.5) \approx -0.8862\)

\(f(1) = 0\)

Punto medio \(x_0 = (0.5+1)/2 = 0.75\)

\(f(0.75) = 2\ln(0.75) - 0.75 + 1 \approx 2(-0.2877) - 0.75 + 1 = -0.5754 - 0.75 + 1 = -0.3254\)

Poiché \(f(0.75) < 0\) e \(f(1) = 0\), la radice si trova nell'intervallo \([0.75, 1]\).

Nuovo intervallo \([a_1, b_1] = [0.75, 1]\). Lunghezza = 0.25.

Iterazione 2:

Intervallo \([a_1, b_1] = [0.75, 1]\)

Punto medio \(x_1 = (0.75+1)/2 = 0.875\)

\(f(0.875) = 2\ln(0.875) - 0.875 + 1 \approx 2(-0.1331) - 0.875 + 1 = -0.2662 - 0.875 + 1 = -0.1412\)

Poiché \(f(0.875) < 0\) e \(f(1) = 0\), la radice si trova nell'intervallo \([0.875, 1]\).

Nuovo intervallo \([a_2, b_2] = [0.875, 1]\). Lunghezza = 0.125.

La lunghezza dell'intervallo (0.125) è minore di 0.2. Possiamo fermarci qui.

Il punto medio di questo intervallo è \(x_2 = (0.875 + 1)/2 = 0.9375\).

Il valore approssimato a meno di un decimo è quindi 0.9 (arrotondando 0.9375 alla prima cifra decimale).

L'equazione è \(x = 2\arctan(x)\).

Possiamo riscriverla come \(f(x) = x - 2\arctan(x) = 0\).

Le derivate sono:

\(f'(x) = 1 - \frac{2}{1+x^2}\)

\(f''(x) = \frac{4x}{(1+x^2)^2}\)

Analizziamo la funzione \(f(x)\):

• \(f(0) = 0 - 2\arctan(0) = 0\). Quindi \(x=0\) è una soluzione (la soluzione nulla).
• Poiché \(f(x)\) è una funzione dispari ( \(f(-x) = -x - 2\arctan(-x) = -x + 2\arctan(x) = -(x - 2\arctan(x)) = -f(x)\) ), se esiste una soluzione positiva, deve esistere anche una soluzione negativa opposta.

Studiamo il segno della derivata prima \(f'(x)\):

\(1 - \frac{2}{1+x^2} > 0 \implies 1 > \frac{2}{1+x^2} \implies 1+x^2 > 2 \implies x^2 > 1 \implies x < -1 \text{ o } x > 1\).

Quindi \(f(x)\) è crescente per \(x < -1\) e per \(x > 1\), e decrescente per \(-1 < x < 1\).

Calcoliamo i massimi e minimi relativi:

• \(x=-1\) è un massimo relativo: \(f(-1) = -1 - 2\arctan(-1) = -1 - 2(-\frac{\pi}{4}) = -1 + \frac{\pi}{2} \approx 0.57\)
• \(x=1\) è un minimo relativo: \(f(1) = 1 - 2\arctan(1) = 1 - 2(\frac{\pi}{4}) = 1 - \frac{\pi}{2} \approx -0.57\)

Dal grafico della funzione:

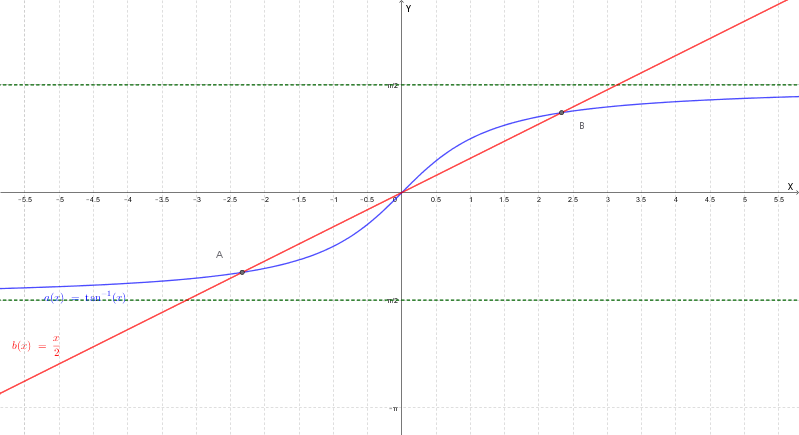
Si deduce che ci sono tre intersezioni con l'asse x (tre soluzioni). Una è \(x=0\), una è positiva e una è negativa. La soluzione positiva si trova nell'intervallo dove \(f(x)\) è crescente dopo il minimo, quindi \(x > 1\).

Per il metodo di Newton, consideriamo la soluzione positiva. Scegliamo un \(x_0\) tale che \(f(x_0)\) e \(f''(x_0)\) abbiano lo stesso segno.

\(f''(x) = \frac{4x}{(1+x^2)^2}\). Per \(x > 0\), \(f''(x) > 0\). Quindi dobbiamo scegliere \(x_0\) tale che \(f(x_0) > 0\).

Poiché \(f(1) \approx -0.57\) e \(\lim_{x \to \infty} f(x) = \lim_{x \to \infty} (x - 2\arctan(x)) = \infty\), esiste una radice per \(x > 1\).

Proviamo con \(x=2\): \(f(2) = 2 - 2\arctan(2) \approx 2 - 2(1.107) = 2 - 2.214 = -0.214\). Ancora negativo.

Proviamo con \(x=3\): \(f(3) = 3 - 2\arctan(3) \approx 3 - 2(1.249) = 3 - 2.498 = 0.502\). Finalmente positivo!

Quindi, scegliamo \(x_0 = 3\).

Iterazione 0: \(x_0 = 3\)

\(f(x_0) = f(3) = 3 - 2\arctan(3) \approx 0.502\)

\(f'(x_0) = f'(3) = 1 - \frac{2}{1+3^2} = 1 - \frac{2}{10} = 1 - 0.2 = 0.8\)

\(x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} = 3 - \frac{0.502}{0.8} = 3 - 0.6275 = 2.3725\)

Iterazione 1: \(x_1 = 2.3725\)

\(f(x_1) = f(2.3725) = 2.3725 - 2\arctan(2.3725) \approx 2.3725 - 2(1.1714) = 2.3725 - 2.3428 = 0.0297\)

\(f'(x_1) = f'(2.3725) = 1 - \frac{2}{1+(2.3725)^2} = 1 - \frac{2}{1+5.6288} = 1 - \frac{2}{6.6288} \approx 1 - 0.3017 = 0.6983\)

\(x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} = 2.3725 - \frac{0.0297}{0.6983} = 2.3725 - 0.04253 = 2.32997\)

Iterazione 2: \(x_2 = 2.32997\)

\(f(x_2) = f(2.32997) = 2.32997 - 2\arctan(2.32997) \approx 2.32997 - 2(1.16484) = 2.32997 - 2.32968 = 0.00029\)

\(f'(x_2) = f'(2.32997) = 1 - \frac{2}{1+(2.32997)^2} = 1 - \frac{2}{1+5.4287} = 1 - \frac{2}{6.4287} \approx 1 - 0.3111 = 0.6889\)

\(x_3 = x_2 - \frac{f(x_2)}{f'(x_2)} = 2.32997 - \frac{0.00029}{0.6889} = 2.32997 - 0.00042 = 2.32955\)

Abbiamo raggiunto una precisione sufficiente. Confrontando \(x_2\) e \(x_3\), vediamo che le prime due cifre decimali sono stabili: \(2.32\). Il valore approssimato a meno di un centesimo è \(2.33\).