Compito del 13 Marzo 1986

Versione accessibile con soluzioni dettagliate

💡 Per una visualizzazione ottimale dei grafici e delle formule, se stai usando lo smartphone disponilo orizzontalmente.

Questo compito è stato assegnato il 13 Marzo 1986 a una classe 5ª del Liceo Scientifico.
Argomenti: studio di funzione esponenziale, soluzione approssimata di un'equazione, metodo di bisezione, metodo delle tangenti, teorema degli zeri, area fra due curve, massimo e minimo per via elementare e con l'uso delle derivate, funzione composta e derivata, Curva di Gauss, distribuzione normale.

Esercizio 1

Si consideri la funzione di equazione: $ f(x) = e^x - x - 2 $

Esistenza degli zeri: Dimostra che la funzione ammette un solo zero negativo $ a $ e un solo zero positivo $ b $.
Metodo di bisezione: Trova un valore approssimato a meno di $ 0,1 $ dello zero negativo $ a $.
Metodo delle tangenti: Trova un valore approssimato a meno di $ 0,01 $ dello zero positivo $ b $.
Studio di funzione: Studia la funzione e rappresentala graficamente la funzione nel piano cartesiano.
Calcolo dell'area: Calcola l'area delimitata dal grafico di $ f(x) $ e $ g(x) = e^x $.
Funzione integrale: Deduci il grafico di $ F(x) = \int_{0}^{x} f(t) \, dt $ dal grafico di $y=f(x)$.

Soluzione Esercizio 1

Isolamento delle radici

Dobbiamo determinare quante soluzioni ha l'equazione $ e^x - x - 2 = 0 $. Definiamo la funzione: $ f(x) = e^x - x - 2 $, che è continua e derivabile su tutto l'asse reale..

1. Studio della monotonia (andamento):

Calcoliamo la derivata prima per capire dove la funzione cresce o decresce: \[ f'(x) = e^x - 1 \]

$ f'(x) = 0 \implies e^x = 1 \implies \mathbf{x = 0} $ (punto stazionario).
$ f'(x) > 0 \implies e^x > 1 \implies \mathbf{x > 0} $ (la funzione cresce).
$ f'(x) < 0 \implies e^x < 1 \implies \mathbf{x < 0} $ (la funzione decresce).

In $ x = 0 $ la funzione ha un minimo relativo: $ f(0) = e^0 - 0 - 2 = -1 $.

2. Ricerca degli intervalli (Teorema degli zeri):

Poiché il minimo è negativo ($-1$) e i limiti agli estremi sono positivi ($ \lim_{x \to \pm \infty} f(x) = +\infty $), la funzione deve tagliare l'asse $ x $ esattamente due volte.

Calcoliamo i valori per individuare i "cambi di segno":

$ f(-2) = e^{-2} + 2 - 2 = e^{-2} \approx \mathbf{0,135 > 0} $
$ f(-1) = e^{-1} + 1 - 2 = e^{-1} - 1 \approx \mathbf{-0,632 < 0} $
$ f(1) = e^1 - 1 - 2 = e - 3 \approx \mathbf{-0,282 < 0} $
$ f(2) = e^2 - 2 - 2 = e^2 - 4 \approx \mathbf{3,389 > 0} $

Conclusione:

Esiste una radice $ a $ nell'intervallo $ (-2, -1) $ perché $ f(-2) > 0 $ e $ f(-1) < 0 $.
Esiste una radice $ b $ nell'intervallo $ (1, 2) $ perché $ f(1) < 0 $ e $ f(2) > 0 $.

b) Metodo di bisezione

Iter.	m (Punto Medio)	f(m)
1	-1,5	-0,277
2	-1,75	-0,076
3	-1,875	+0,028

Risultato: $ a \approx -1,8 $

c) Metodo delle tangenti

Per trovare lo zero positivo $ b \in [1, 2] $, verifichiamo le condizioni di applicabilità:

Scelta del punto iniziale $ x_0 $:
La derivata seconda è $ f''(x) = e^x $, sempre positiva (funzione convessa).
Poiché $ f(2) \approx 3,389 $ è positivo (concorde con $ f''(x) $), scegliamo $ x_0 = 2 $ come punto di partenza.

Utilizziamo la formula ricorsiva: $ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} $ con $ f'(x) = e^x - 1 $

Iterazioni del calcolo:

$ x_0 = 2 $
$ x_1 = 2 - \frac{e^2 - 4}{e^2 - 1} \approx 2 - \frac{3,389}{6,389} \approx \mathbf{1,47} $
$ x_2 = 1,47 - \frac{e^{1,47} - 1,47 - 2}{e^{1,47} - 1} \approx 1,47 - \frac{0,879}{3,349} \approx \mathbf{1,21} $
$ x_3 = 1,21 - \frac{e^{1,21} - 1,21 - 2}{e^{1,21} - 1} \approx 1,21 - \frac{0,143}{2,353} \approx \mathbf{1,15} $
$ x_4 = 1,15 - \frac{e^{1,15} - 1,15 - 2}{e^{1,15} - 1} \approx 1,15 - \frac{0,008}{2,158} \approx \mathbf{1,146} $

Risultato: Lo zero positivo approssimato a meno di un centesimo è $ b \approx 1,15 $.

d) Studio di funzione e Grafico

1. Dominio:

La funzione $ f(x) = e^x - x - 2 $ è definita per ogni $ x \in \mathbb{R} $.
Il Dominio è: $ D = (-\infty, +\infty) $.

2. Simmetrie:

$ f(-x) = e^{-x} + x - 2 $. Poiché $ f(-x) \neq f(x) $ e $ f(-x) \neq -f(x) $, la funzione non è né pari né dispari.

3. Intersezioni con gli assi:

Asse y: Per $ x = 0 $, $ f(0) = e^0 - 0 - 2 = -1 $. Il punto è $ (0, -1) $.
Asse x: Come dimostrato al punto a), la funzione ha due zeri: $ \alpha \approx -1,84 $ e $ \beta \approx 1,14 $.

4. Limiti e asintoti:

A destra ($ x \to +\infty $):

$ \lim_{x \to +\infty} (e^x - x - 2) = +\infty $.
Non c'è asintoto orizzontale. Verifichiamo l'obliquo: $ \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{e^x}{x} = +\infty $. Nessun asintoto obliquo a destra.

A sinistra ($ x \to -\infty $):

$ \lim_{x \to -\infty} (e^x - x - 2) = +\infty $.
Verifichiamo l'asintoto obliquo $ y = mx + q $:
$ m = \lim_{x \to -\infty} \frac{f(x)}{x} = -1 $;
$ q = \lim_{x \to -\infty} [f(x) - (-x)] = -2 $.
Esiste un asintoto obliquo a sinistra: $ y = -x - 2 $.

5. Derivata prima e monotonia:

$ f'(x) = e^x - 1 $.
Segno: $ f'(x) > 0 \implies x > 0 $.

Per $ x < 0 $: funzione decrescente.
Per $ x > 0 $: funzione crescente.
In $ x = 0 $: punto di minimo relativo e assoluto $ M(0, -1) $.

6. Derivata seconda e concavità:

$ f''(x) = e^x $.
Poiché $ e^x > 0 $ per ogni $ x $, la funzione volge sempre la concavità verso l'alto.

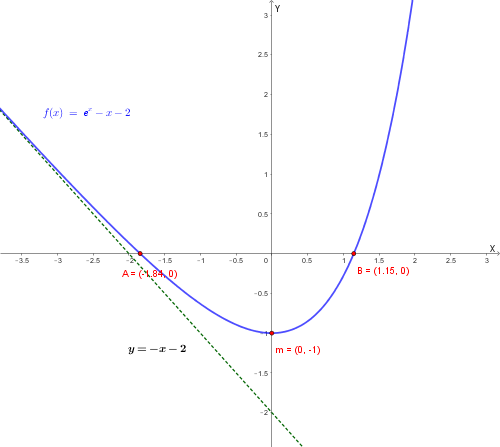
Grafico della funzione con evidenziato l'asintoto obliquo

e) Calcolo dell'Area

Dobbiamo calcolare l'area della regione di piano compresa tra le curve $ f(x) = e^x - x - 2 $ e $ g(x) = e^x $, nell'intervallo dove la seconda sovrasta la prima.

1. Ricerca del punto di intersezione:

Uguagliamo le due funzioni per trovare dove si incontrano:

\[ f(x) = g(x) \implies e^x - x - 2 = e^x \] Semplificando $ e^x $: \[ -x - 2 = 0 \implies \mathbf{x = -2} \]

2. Rappresentazione grafica:

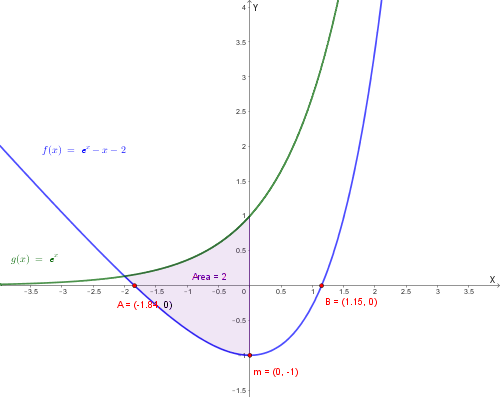
In evidenza l'area tra $ g(x) = e^x $ (sopra) e $ f(x) $ (sotto) nell'intervallo $[-2, 0]$.

3. Calcolo dell'integrale:

L'area si ottiene calcolando l'integrale della differenza tra la funzione "superiore" $ g(x) $ e quella "inferiore" $ f(x) $:

\text{Area} = \int_{-2}^{0} [g(x) - f(x)] \, dx \] \[ \text{Area} = \int_{-2}^{0} [e^x - (e^x - x - 2)] \, dx \] \[ \text{Area} = \int_{-2}^{0} (x + 2) \, dx

Calcoliamo la primitiva e applichiamo la formula di Newton-Leibniz:

\[ \text{Area} = \left[ \frac{x^2}{2} + 2x \right]_{-2}^{0} \]

Sostituendo gli estremi:

\[ \text{Area} = (0) - \left( \frac{(-2)^2}{2} + 2(-2) \right) \] \[ \text{Area} = - \left( \frac{4}{2} - 4 \right) = - (2 - 4) = \mathbf{2} \]

Il valore dell'area cercata è quindi 2.

f) Studio della funzione integrale F(x) per $ x \ge 0 $

Sia $ F(x) = \int_{0}^{x} f(t) \, dt $ con $ x \ge 0 $. Vediamo come dedurre l'andamento della funzione integrale partendo dal grafico di $ f(x) $:

1. Punto di partenza:

Per $ x = 0 $, l'integrale ha gli estremi coincidenti:
$ F(0) = \int_{0}^{0} f(t) \, dt = \mathbf{0} $.
La funzione integrale parte quindi dall'origine degli assi $ (0,0) $.

2. Studio della Crescenza (Derivata prima):

Ricordiamo che $ F'(x) = f(x) $. Per capire dove $ F(x) $ cresce o decresce, guardiamo il segno di $ f(x) $ per $ x \ge 0 $:

In $ x = 0 $: Abbiamo visto che $ f(0) = -1 $. Quindi la funzione integrale inizia il suo percorso decrescendo.
Intervallo $ 0 \le x < b $: (dove $ b \approx 1,14 $). In questo tratto la funzione $ f(x) $ si trova sotto l'asse delle ascisse (negativa), quindi $ F(x) $ decresce.
In $ x = b $: Poiché $ f(b) = 0 $, la derivata $ F'(b) $ è nulla. In questo punto $ F(x) $ raggiunge il suo Minimo relativo.
Per $ x > b $: In questo tratto $ f(x) $ diventa positiva, di conseguenza $ F(x) $ cresce tendendo a $ +\infty $.

3. Studio della Concavità (Derivata seconda):

La derivata seconda di $ F(x) $ corrisponde alla derivata prima di $ f(x) $, ovvero $ F''(x) = f'(x) $:

Sappiamo che per $ x > 0 $, la derivata $ f'(x) $ è sempre positiva (come visto nello studio della monotonia di $ f $).
Pertanto, $ F(x) $ avrà sempre la concavità rivolta verso l'alto per tutto l'intervallo considerato.

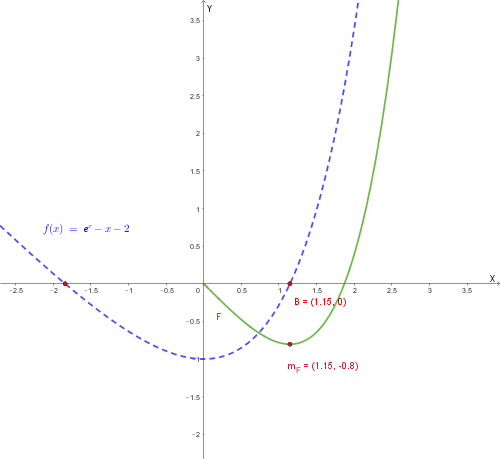
Grafico della funzione integrale F(x) per x maggiore o uguale a 0

Andamento di $ F(x) $ per $ x \ge 0 $: parte dall'origine, decresce fino al minimo in $ b \approx 1,14 $ e poi cresce con concavità verso l'alto.

Esercizio 2

Dimostra le seguenti proprietà, prima per via elementare e poi usando le derivate:

Somma minima: Dimostra che la somma di due numeri positivi con prodotto costante è minima quando i numeri sono uguali. Spiegane il significato geometrico.
Prodotto massimo: Dimostra che il prodotto di due numeri positivi con somma costante è massimo quando i numeri sono uguali. Spiegane il significato geometrico.

Soluzione Esercizio 2

1) Somma minima a prodotto costante

Dati due numeri il cui prodotto è costante $ x \cdot y = p $, cerchiamo il valore minimo della loro somma $ S = x + y $.

A) Via Elementare:

Usiamo l'identità algebrica:
\[ (x+y)^2 = (x-y)^2 + 4xy \]

Sostituendo il prodotto costante $ p $:
\[ (x+y)^2 = (x-y)^2 + 4p \]

La somma $ (x+y) $ è minima quando il termine al quadrato $ (x-y)^2 $ è nullo (poiché un quadrato non può mai essere negativo).
Quindi il minimo si ha quando: $ x = y $.

B) Via Analitica (Uso delle Derivate)

Per trovare il valore minimo utilizzando il calcolo infinitesimale, seguiamo questi passaggi:

1. Costruzione della funzione:

Dalla condizione $ x \cdot y = p $, ricaviamo la seconda variabile: $ y = \frac{p}{x} $.
La funzione "Somma" da minimizzare diventa: \[ f(x) = x + \frac{p}{x} \]

2. Calcolo della derivata prima:

Deriviamo $ f(x) $ sapendo che la derivata di $ x $ è $ 1 $ e quella di $ \frac{1}{x} $ è $ -\frac{1}{x^2} $:

\[ f'(x) = 1 - \frac{p}{x^2} = \frac{x^2 - p}{x^2} \]

3. Studio del segno della derivata ($ x > 0 $):

Il denominatore $ x^2 $ è sempre positivo, quindi studiamo solo il numeratore $ x^2 - p $:

Decrescenza: Per $ 0 < x < \sqrt{p} $, la derivata è negativa ($ f'(x) < 0 $).
Punto stazionario: In $ x = \sqrt{p} $ la derivata è nulla.
Crescenza: Per $ x > \sqrt{p} $, la derivata è positiva ($ f'(x) > 0 $).

4. Conclusione:

In $ x = \sqrt{p} $ abbiamo un Minimo relativo e assoluto.

Calcoliamo il valore di $ y $:

\[ y = \frac{p}{\sqrt{p}} = \mathbf{\sqrt{p}} \]

Il minimo si ottiene quando i due numeri sono uguali: $ x = y = \sqrt{p} $.

Significato Geometrico:

Tra tutti i rettangoli con la stessa area, il quadrato è quello che ha il perimetro minore.

Infatti, se $ x $ e $ y $ sono i lati del rettangolo, l'area è $ xy = p $ e il perimetro è $ 2(x+y) $. Minimizzare la somma dei lati equivale a minimizzare il perimetro.

2) Prodotto massimo a somma costante

Dati due numeri la cui somma è costante $ x + y = s $, cerchiamo il valore massimo del loro prodotto $ P = x \cdot y $.

Metodo 1: Utilizzo dell'identità algebrica

Partiamo dalla relazione algebrica:
\[ (x+y)^2 = (x-y)^2 + 4xy \]

Isoliamo il termine del prodotto $ 4xy $:
\[ 4xy = (x+y)^2 - (x-y)^2 \]

Sostituendo la somma costante $ s $:
\[ 4xy = s^2 - (x-y)^2 \]

Poiché $ s^2 $ non cambia, il prodotto è massimo quando la quantità che sottraiamo $ (x-y)^2 $ è la più piccola possibile.
Il valore minimo di un quadrato è $ 0 $, che si ottiene quando:
$ x - y = 0 \implies x = y $.

Metodo 2: Studio della parabola

Dalla relazione $ x + y = s $, ricaviamo $ y = s - x $.
Esprimiamo il prodotto $ P $ in funzione di una sola variabile:

\[ P(x) = x(s - x) = -x^2 + sx \]

Questa è l'equazione di una parabola con la concavità rivolta verso il basso.

Il punto di massimo si trova nel Vertice della parabola:

\[ x_V = -\frac{b}{2a} = -\frac{s}{2(-1)} = \mathbf{\frac{s}{2}} \]

Se $ x = \frac{s}{2} $, allora anche $ y = s - \frac{s}{2} = \mathbf{\frac{s}{2}} $.

Il prodotto è massimo quando i due numeri sono uguali: $ x = y $.

B) Via Analitica (Uso delle Derivate)

Utilizziamo il calcolo infinitesimale per confermare il punto di massimo:

1. Funzione da massimizzare:

Sostituendo $ y = s - x $, la funzione Prodotto è: \[ f(x) = x(s - x) = -x^2 + sx \]

2. Calcolo della derivata prima e segno:

\[ f'(x) = -2x + s \]

Studiamo il segno $ f'(x) > 0 $:

\[ -2x + s > 0 \implies 2x < s \implies \mathbf{x < \frac{s}{2}} \]

Per $ x < \frac{s}{2} $: la funzione cresce ($ f'(x) > 0 $).
In $ x = \frac{s}{2} $: abbiamo il punto di Massimo ($ f'(x) = 0 $).
Per $ x > \frac{s}{2} $: la funzione decresce ($ f'(x) < 0 $).

3. Conclusione:

Il massimo si ha per $ x = \frac{s}{2} $. Calcolando la $ y $:

\[ y = s - \frac{s}{2} = \mathbf{\frac{s}{2}} \]

Quindi il massimo si ha per $ x = y $.

Significato Geometrico:

Tra tutti i rettangoli con lo stesso perimetro (somma dei lati costante), il quadrato è quello che ha l'area massima.

Infatti, se la somma dei lati $ x+y = s $ è costante, allora è costante anche il perimetro $ 2(x+y) $. L'area $ xy $ è massima quando i lati sono uguali.

Esercizio 3

1. Data la funzione $ g(x) = e^{f(x)} $, dove $ f(x) $ è derivabile due volte in $ x=1 $ e tale che $ f'(1) = 0, \ f''(1) \neq 0 $, stabilisci la natura del punto $ x=1 $.

2. Applica quanto dimostrato al caso $ f(x) = -(x-1)^2 $, studia la funzione $ g(x) = e^{-(x-1)^2} $ e rappresentane il grafico qualitativo.

3. Esponi i legami tra questa funzione e la curva di Gauss (distribuzione normale) utilizzata in probabilità e statistica.

Soluzione Esercizio 3

1. Analisi teorica generale

Determiniamo la natura del punto $ x=1 $ attraverso lo studio delle derivate di $ g(x) = e^{f(x)} $:

Derivata prima:

\[ g'(x) = e^{f(x)} \cdot f'(x) \]

In $ x=1 $, poiché $ f'(1)=0 $, abbiamo:
$ g'(1) = e^{f(1)} \cdot 0 = \mathbf{0} $.

Il punto è stazionario (tangente orizzontale).

Derivata seconda:

\[ g''(x) = e^{f(x)} \cdot (f'(x))^2 + e^{f(x)} \cdot f''(x) \]

In $ x=1 $, essendo $ f'(1)=0 $, il calcolo si semplifica:
$ g''(1) = e^{f(1)} \cdot f''(1) $.

Dato che $ e^{f(1)} $ è sempre positivo, il segno della derivata seconda dipende solo da $ f''(1) $. Essendo diverso da zero, $ x=1 $ è un punto di estremo relativo (massimo o minimo).

2. Caso particolare: $ f(x) = -(x-1)^2 $

Studiamo la funzione $ g(x) = e^{-(x-1)^2} $ analizzandone ogni aspetto:

Dominio: La funzione è definita per ogni valore di $ x $, quindi $ D = \mathbb{R} $.
Simmetria: La funzione base $ y = e^{-x^2} $ è una funzione pari (simmetrica rispetto all'asse $ y $).
La nostra funzione $ g(x) $ ha l'argomento traslato di $ 1 $: questo significa che l'intero grafico è spostato a destra. La funzione è quindi simmetrica rispetto alla retta $ x = 1 $.
Segno e Intersezioni:
- Segno: Poiché l'esponenziale è sempre positivo, $ g(x) > 0 $ per ogni $ x $. Il grafico si trova tutto sopra l'asse $ x $.
- Intersezione asse $ x $: Nessuna (la funzione non tocca mai lo zero).
- Intersezione asse $ y $: Poniamo $ x = 0 $:
  $ g(0) = e^{-(0-1)^2} = e^{-1} = \mathbf{\frac{1}{e} \approx 0,37} $.
Limiti (Asintoti): Per $ x $ che tende a valori molto grandi (positivi o negativi), l'esponente diventa un numero negativo enorme: $\lim_{x \to \pm\infty} e^{-(x-1)^2} = 0^+$ L'asse delle ascisse ($ y = 0 $) è un asintoto orizzontale.
Studio del Massimo (Derivata):
Calcoliamo la derivata prima per verificare la crescita:
\[ g'(x) = e^{-(x-1)^2} \cdot [-2(x-1)] = \mathbf{-2(x-1)e^{-(x-1)^2}} \]
Studiamo il segno di $ g'(x) $:
- Per $ x < 1 $: $ g'(x) > 0 $ (la funzione cresce).
- In $ x = 1 $: $ g'(x) = 0 $ (punto di massimo).
- Per $ x > 1 $: $ g'(x) < 0 $ (la funzione decresce).
Il valore del massimo è: $ g(1) = e^0 = \mathbf{1} $.

Grafico della funzione $ g(x) = e^{-(x-1)^2} $:

Grafico della funzione gaussiana traslata in x=1

Il picco della "campana" si trova nel punto (1, 1). La curva è simmetrica rispetto alla retta verticale $ x=1 $.

3. Collegamento con la Curva di Gauss

La funzione studiata ha la forma tipica della distribuzione normale o Gaussiana. La sua espressione generale in statistica è:

\[ \phi(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \]

Confronto e calcolo dei parametri:

Confrontando la nostra funzione $ g(x) = e^{-(x-1)^2} $ con il modello teorico, possiamo identificare i parametri fondamentali:

Media ($ \mu $): Poiché nell'esponente abbiamo il termine $ (x-1) $, la media è $ \mu = 1 $.
Questo valore rappresenta il centro di simmetria e la posizione del valore più probabile (Moda).
Deviazione Standard ($ \sigma $): Uguagliando gli esponenti $ \frac{1}{2\sigma^2} = 1 $, ricaviamo:
\[ \sigma^2 = \frac{1}{2} \implies \sigma = \frac{1}{\sqrt{2}} = \mathbf{\frac{\sqrt{2}}{2} \approx 0,707} \]
Questo parametro indica la dispersione dei dati: una $ \sigma $ piccola produce una campana stretta e alta, una $ \sigma $ grande produce una campana larga e piatta.

Significato dei flessi:

In statistica, i punti di flesso della Gaussiana si trovano sempre a distanza di una deviazione standard dalla media:

\[ x = \mu \pm \sigma \] Per la nostra funzione, i flessi si trovano infatti in: \[ \mathbf{x = 1 \pm \frac{\sqrt{2}}{2}} \]

Significato geometrico del massimo:
Rappresenta il valore medio della distribuzione (la Moda). Geometricamente, è il punto più alto della curva dove la densità di probabilità è massima.

💬 Ti è stata utile questa risorsa?

✉️ Invia feedback

Il tuo parere è importante per migliorare la chiarezza di queste risorse.
(Si aprirà il tuo programma email)

Compito del 13 Marzo 1986

Esercizio 1

Soluzione Esercizio 1

Isolamento delle radici

b) Metodo di bisezione

c) Metodo delle tangenti

d) Studio di funzione e Grafico

e) Calcolo dell'Area

f) Studio della funzione integrale F(x) per \( x \ge 0 \)

Esercizio 2

Soluzione Esercizio 2

1) Somma minima a prodotto costante

B) Via Analitica (Uso delle Derivate)

2) Prodotto massimo a somma costante

B) Via Analitica (Uso delle Derivate)

Esercizio 3

Soluzione Esercizio 3

1. Analisi teorica generale

2. Caso particolare: \( f(x) = -(x-1)^2 \)

3. Collegamento con la Curva di Gauss