



📚 Disponibile anche in versione DSA
Questo compito è stato assegnato il 13 Marzo 1986 a una classe 5ª del Liceo Scientifico.
Argomenti: studio di funzione esponenziale, soluzione approssimata di un'equazione, metodo di bisezione, metodo delle tangenti, teorema degli zeri, area fra due curve,
massimo e minimo per via elementare e con l'uso delle derivate, funzione composta e derivata, Curva di Gauss, distribuzione normale.
Consideri la funzione di equazione \( f(x) = e^x - x - 2 \).
a) Dimostra che la funzione ammette un solo zero negativo \( a \) ed un solo zero positivo \( b \).
b) Utilizzando il Metodo di bisezione, trova un valore approssimato a meno di un decimo del valore negativo \( a \).
c) Utilizzando il Metodo delle tangenti (dopo aver dimostrato l'applicabilità e giustificato la scelta del punto iniziale dell'iterazione), trova un valore approssimato a meno di un centesimo del valore positivo \( b \).
d) Studia la funzione e rappresentala graficamente nel piano cartesiano.
e) Calcola l'area della regione finita di piano delimitata dal grafico di \( f \) e dal grafico della funzione \( g(x) = e^x \).
f) Indicata con \( F \) la funzione integrale \( F(x) = \int_{0}^{x} f(t) \, dt \), deduci il suo grafico qualitativo a partire dal grafico di \( y = f(x) \) per \( x \ge 0 \).
Consideriamo la funzione \( f(x) = e^x - x - 2 \). La funzione è continua e derivabile in tutto \( \mathbb{R} \). Per isolare le radici, calcoliamo alcuni valori significativi:
Per il Teorema degli zeri:
Studiando la derivata prima \( f'(x) = e^x - 1 \), osserviamo che \( f'(x) = 0 \) per \( x = 0 \). La funzione decresce per \( x < 0 \) e cresce per \( x > 0 \). Essendo monotona negli intervalli considerati, le radici \( a \) e \( b \) sono uniche.
Applichiamo il metodo all'intervallo \( [-2, -1] \) con \( f(-2) > 0 \) e \( f(-1) < 0 \):
| Iter. | a | b | m (punto medio) | f(m) |
|---|---|---|---|---|
| 1 | -2,0 | -1,0 | -1,5 | -0,277 |
| 2 | -2,0 | -1,5 | -1,75 | -0,076 |
| 3 | -2,0 | -1,75 | -1,875 | +0,028 |
| 4 | -1,875 | -1,75 | -1,8125 | -0,024 |
Il valore approssimato a meno di un decimo è \( a \approx -1,8 \).
Per \( x > 0 \), la derivata seconda è \( f''(x) = e^x \), che è sempre positiva. Nell'intervallo \( [1, 2] \), \( f''(x) \) ha segno costante e concorda con il segno di \( f(2) > 0 \). Scegliamo quindi \( x_0 = 2 \) come punto iniziale per l'iterazione.
Formula di iterazione: \( x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \), con \( f'(x) = e^x - 1 \)
Lo zero positivo approssimato a meno di un centesimo è quindi \( b \approx 1,15 \) (o \( 1,14 \) a seconda degli arrotondamenti intermedi).
1. Dominio: La funzione \( f(x) = e^x - x - 2 \) è definita per ogni \( x \in \mathbb{R} \). Quindi \( D = (-\infty, +\infty) \).
2. Simmetrie: \( f(-x) = e^{-x} + x - 2 \). Poiché \( f(-x) \neq f(x) \) e \( f(-x) \neq -f(x) \), la funzione non è né pari né dispari.
3. Intersezioni con gli assi:
4. Limiti e asintoti:
5. Derivata prima e monotonia:
\( f'(x) = e^x - 1 \).
Studiamo il segno: \( e^x - 1 > 0 \Rightarrow e^x > 1 \Rightarrow x > 0 \).
6. Derivata seconda e concavità:
\( f''(x) = e^x \).
Poiché \( e^x > 0 \) per ogni \( x \in \mathbb{R} \), la funzione volge sempre la concavità verso l'alto (è convessa). Non sono presenti punti di flesso.
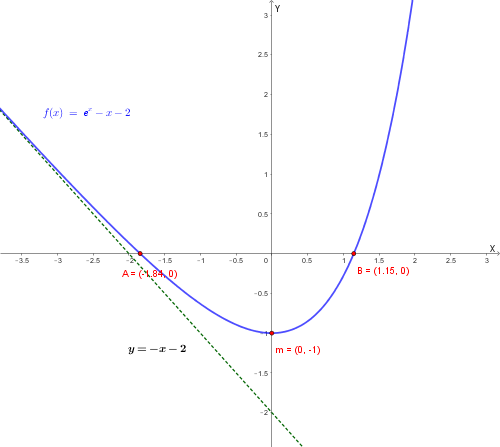
Grafico di \( f(x) = e^x - x - 2 \) con evidenziato l'asintoto obliquo
Rappresentiamo nello stesso piano cartesiano le due funzioni \( f(x) \) e \( g(x) = e^x \).
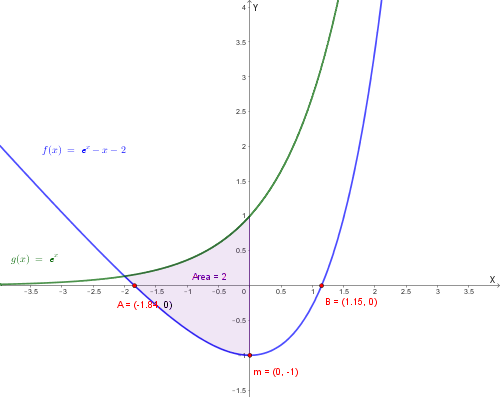
L'intersezione si ha quando \( f(x) = g(x) \Rightarrow e^x - x - 2 = e^x \Rightarrow -x - 2 = 0 \Rightarrow x = -2 \). L'area è data da: \[ \text{Area} = \int_{-2}^{0} [g(x) - f(x)] \, dx = \int_{-2}^{0} [e^x - (e^x - x - 2)] \, dx = \int_{-2}^{0} (x + 2) \, dx \] \[ \text{Area} = \left[ \frac{x^2}{2} + 2x \right]_{-2}^{0} = 0 - \left( \frac{4}{2} - 4 \right) = 2 \]
Sia \( F(x) = \int_{0}^{x} f(t) \, dt \). Per il teorema fondamentale del calcolo, \( F'(x) = f(x) \). Osserviamo che \( F(0) = 0 \). Per \( x \ge 0 \), \( F(x) \) decresce dove \( f(x) < 0 \) (fino a \( b \)) e cresce dove \( f(x) > 0 \). In \( x = b \) la funzione \( F(x) \) presenta un minimo relativo.
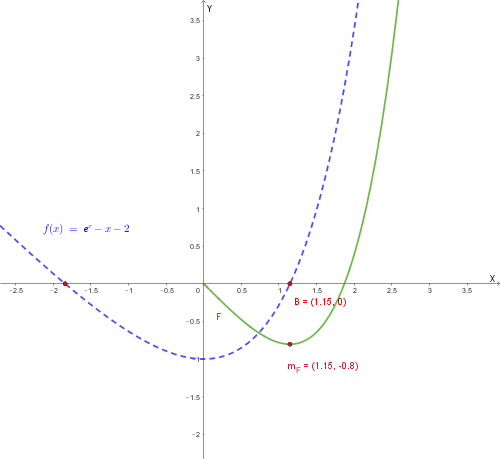
In blu tratteggiato \( f(x) \), in verde la funzione integrale \( F(x) \)
Dimostra le seguenti proprietà prima per via elementare, poi con l'utilizzo delle derivate:
a) La somma di due numeri positivi di dato prodotto è minima se i due numeri sono uguali. Qual è il significato geometrico di questa proprietà?
b) Il prodotto di due numeri positivi di data somma è massimo se i due numeri sono uguali. Qual è il significato geometrico di questa proprietà?
Siano \( x \) e \( y \) due numeri reali positivi tali che il loro prodotto sia costante: \( x \cdot y = p \). Dobbiamo dimostrare che la loro somma \( S = x + y \) è minima quando \( x = y \).
Consideriamo l'identità: \[ (x+y)^2 = (x-y)^2 + 4xy \] Sostituendo il prodotto costante \( xy = p \), abbiamo: \[ (x+y)^2 = (x-y)^2 + 4p \] Poiché \( 4p \) è una costante, il valore di \( (x+y)^2 \) (e quindi di \( x+y \), essendo i numeri positivi) è minimo quando il termine al quadrato \( (x-y)^2 \) è minimo. Il valore minimo di un quadrato è \( 0 \), che si ottiene quando: \[ x - y = 0 \Rightarrow x = y \]
Dalla condizione \( xy = p \) ricaviamo \( y = \frac{p}{x} \). La funzione somma da minimizzare è: \[ f(x) = x + \frac{p}{x} \] Calcoliamo la derivata prima: \[ f'(x) = 1 - \frac{p}{x^2} = \frac{x^2 - p}{x^2} \] Studiamo il segno di \( f'(x) \) per \( x > 0 \): \[ \frac{x^2 - p}{x^2} > 0 \Rightarrow x^2 - p > 0 \Rightarrow x > \sqrt{p} \]
Si ha quindi un minimo relativo e assoluto in \( x = \sqrt{p} \). In tal caso \( y = \frac{p}{\sqrt{p}} = \sqrt{p} \), quindi il minimo si ha per \( x = y \).
Siano \( x \) e \( y \) due numeri reali positivi tali che la loro somma sia costante: \( x + y = s \). Dobbiamo dimostrare che il loro prodotto \( P = x \cdot y \) è massimo quando \( x = y \).
Metodo 1: Utilizzo dell'identità algebrica
Partiamo dalla stessa relazione utilizzata nel punto precedente: \[ (x+y)^2 = (x-y)^2 + 4xy \] Ricaviamo l'espressione del prodotto \( 4xy \): \[ 4xy = (x+y)^2 - (x-y)^2 \] Sostituendo la somma costante \( x+y = s \), abbiamo: \[ 4xy = s^2 - (x-y)^2 \] Poiché \( s^2 \) è una costante, il valore di \( 4xy \) (e quindi di \( xy \)) è massimo quando la quantità che sottraiamo è minima. Il valore minimo del quadrato \( (x-y)^2 \) è \( 0 \), che si ottiene quando: \[ x - y = 0 \Rightarrow x = y \]
Metodo 2: Studio della parabola
Se \( x + y = s \), possiamo scrivere il prodotto come una funzione della sola variabile \( x \): \[ P(x) = x(s - x) = -x^2 + sx \] Questa funzione rappresenta una parabola con la concavità rivolta verso il basso. Il suo punto di massimo si trova nel vertice, la cui ascissa è: \[ x_V = -\frac{b}{2a} = -\frac{s}{2(-1)} = \frac{s}{2} \] Dalla relazione \( x+y=s \), se \( x = s/2 \), allora anche \( y = s - s/2 = s/2 \). Quindi il prodotto è massimo quando i due numeri sono uguali: \( x = y \).
Dalla condizione \( x + y = s \) ricaviamo \( y = s - x \). La funzione prodotto da massimizzare è: \[ f(x) = x(s - x) = -x^2 + sx \] Calcoliamo la derivata prima: \[ f'(x) = -2x + s \] Studiamo il segno di \( f'(x) \): \[ -2x + s > 0 \Rightarrow 2x < s \Rightarrow x < \frac{s}{2} \]
Si ha quindi un massimo relativo e assoluto in \( x = \frac{s}{2} \). In tal caso \( y = s - \frac{s}{2} = \frac{s}{2} \), quindi il massimo si ha per \( x = y \).
1. Data la funzione \( g(x) = e^{f(x)} \), dove \( f(x) \) è una funzione derivabile due volte in \( x=1 \) ed è tale che: \[ f'(1) = 0, \quad f''(1) \neq 0 \] stabilisci se nel punto di ascissa \( x=1 \) la funzione \( g(x) \) presenta un massimo o minimo relativo oppure un punto di flesso.
2. Applica quanto dimostrato al caso particolare in cui \( f(x) = -(x-1)^2 \). Studia la funzione \( g(x) = e^{-(x-1)^2} \), verificandone la natura nel punto \( x=1 \) e rappresentandone il grafico qualitativo.
3. Esponi quali legami esistono tra la funzione studiata al punto precedente e la curva di Gauss (o distribuzione normale) utilizzata in probabilità e statistica, commentando in particolare il significato geometrico del punto di massimo.
Data la funzione composta \( g(x) = e^{f(x)} \), determiniamo la natura del punto \( x=1 \) attraverso lo studio delle derivate.
Derivata prima:
Utilizziamo la regola \( D[e^{f(x)}] = e^{f(x)} \cdot f'(x) \).
In \( x=1 \), poiché \( f'(1)=0 \), abbiamo:
\[ g'(1) = e^{f(1)} \cdot 0 = 0 \]
Il punto è dunque stazionario (a tangente orizzontale).
Derivata seconda:
Applicando la regola del prodotto alla derivata prima:
\[ g''(x) = e^{f(x)} \cdot (f'(x))^2 + e^{f(x)} \cdot f''(x) \]
In \( x=1 \), essendo \( f'(1)=0 \), il primo addendo si annulla:
\[ g''(1) = e^{f(1)} \cdot (0)^2 + e^{f(1)} \cdot f''(1) = e^{f(1)} \cdot f''(1) \]
Poiché \( e^{f(1)} \) è una quantità sempre positiva, il segno di \( g''(1) \) dipende esclusivamente da quello di \( f''(1) \). Dato che per ipotesi \( f''(1) \neq 0 \), concludiamo che \( x=1 \) è un punto di estremo relativo (massimo o minimo).
Studiamo la funzione \( g(x) = e^{-(x-1)^2} \):
Grafico della funzione \( g(x) = e^{-(x-1)^2} \):
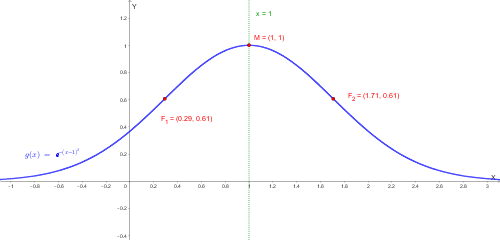
Rappresentazione qualitativa: il picco si trova nel punto (1, 1).
La funzione studiata ha la forma tipica della distribuzione normale o Gaussiana. La sua espressione generale in statistica è: \[ \phi(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \]
Confronto e calcolo dei parametri:
Confrontando la nostra funzione \( g(x) = e^{-(x-1)^2} \) con il modello statistico, possiamo identificare i parametri:
Significato dei flessi:
In statistica, i punti di flesso della Gaussiana si trovano sempre a distanza di una deviazione standard dalla media (\( \mu \pm \sigma \)). Per la nostra funzione, i flessi si trovano infatti in: \[ x = 1 \pm \frac{\sqrt{2}}{2} \]
Grafico della funzione \( g(x) = e^{-(x-1)^2} \):

Il picco della campana (moda) si trova in x = 1.