Soluzione Esercizio 1
a) Determinazione della funzione \( f(x) \)
Calcoliamo le primitive di \( g(x) \):
\[ f(x) = \int (3x^2 + 2x + a) dx = x^3 + x^2 + ax + c \]
Calcoliamo le derivate per trovare il flesso:
- \( f'(x) = 3x^2 + 2x + a \)
- \( f''(x) = 6x + 2 \)
Il flesso si ha per \( f''(x)=0 \Rightarrow 6x+2=0 \Rightarrow \mathbf{x = -1/3} \).
Imponendo la pendenza della tangente \( f'(-1/3) = -4 \) e il passaggio per la retta \( y = -4x - 4 \), si ottengono i parametri \( a = -1 \) e \( c = -4 \).
Risultato: \( f(x) = x^3 + x^2 - x - 4 \)
b) Studio della funzione \( f(x) \)
1. Dominio e Intersezioni:
Il dominio è \( \mathbb{R} \). L'intersezione con l'asse \( y \) è \( (0, -4) \).
2. Ricerca dello zero (Metodo di Bisezione e Tangenti):
Poiché \( f(1) = -3 \) e \( f(2) = 6 \), lo zero \( \alpha \) è tra 1 e 2.
Usando il metodo di bisezione (dimezzando l'intervallo) o quello delle tangenti di Newton (partendo da \( x_0 = 1,5 \)), si ottiene:
Lo zero è \( \alpha \approx 1,49 \)
3. Monotonia (Derivata Prima):
\( f'(x) = 3x^2 + 2x - 1 \). Risolvendo \( f'(x)=0 \) otteniamo \( x = -1 \) e \( x = 1/3 \).
- Massimo relativo: in \( x = -1 \), con \( f(-1) = -3 \).
- Minimo relativo: in \( x = 1/3 \), con \( f(1/3) \approx -4,19 \).
La funzione cresce fino a \( -1 \), decresce fino a \( 1/3 \) e poi cresce definitivamente, tagliando l'asse \( x \) in \( \alpha \approx 1,49 \).
4. Concavità (Derivata Seconda):
\( f''(x) = 6x + 2 \). Il flesso è in \( x = -1/3 \) con \( f(-1/3) \approx -3,59 \). La curva è concava verso il basso per \( x < -1/3 \) e verso l'alto per \( x > -1/3 \).
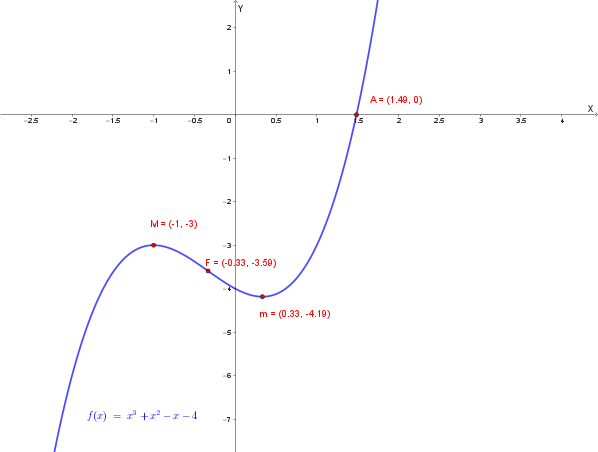
Grafico di \( y = x^3 + x^2 - x - 4 \)
c) Grafico di \( y = \ln[f(x)] \)
1. Dominio: Il logaritmo esiste solo se l'argomento è positivo: \( f(x) > 0 \). Dallo studio precedente sappiamo che questo accade per \( \mathbf{x > \alpha \approx 1,49} \).
2. Asintoti:
- Verticale: Quando \( x \) si avvicina ad \( \alpha \) da destra, \( f(x) \) tende a zero positivo, quindi:
\[ \lim_{x \to 1,49^+} \ln[f(x)] = -\infty \]
- Comportamento all'infinito: Per \( x \to +\infty \), \( \ln[f(x)] \to +\infty \).
3. Monotonia e Asintoto Obliquo:
La derivata è \( \frac{f'(x)}{f(x)} \). Poiché per \( x > 1,49 \) sia \( f' \) che \( f \) sono positivi, la funzione è sempre crescente.
Non esiste asintoto obliquo perché la crescita logaritmica è più lenta di quella lineare:
\[ \lim_{x \to +\infty} \frac{\ln[f(x)]}{x} = 0 \]
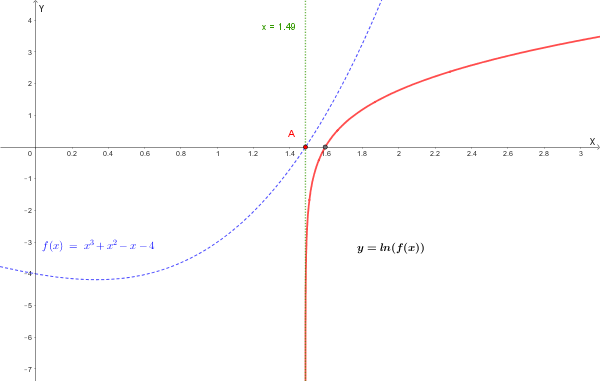
Grafico di \( y = \ln(x^3 + x^2 - x - 4) \)
Soluzione Esercizio 2
1. Definizione delle variabili e Figura
Indichiamo con:
- \( r \) = raggio della base del cilindro e della semisfera
- \( h \) = altezza del cilindro
- \( V \) = volume totale (costante nota)
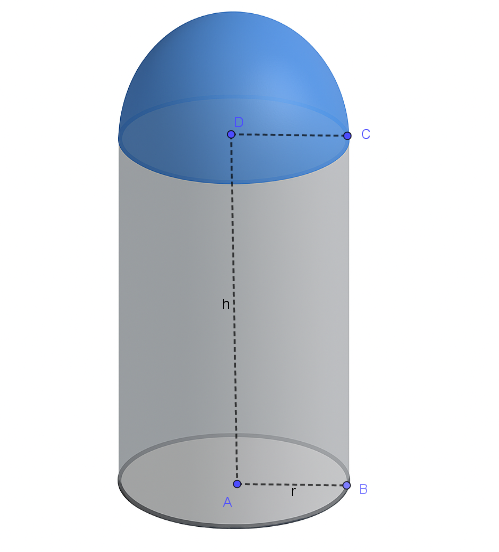
Rappresentazione del solido composto
2. Esprimere l'altezza \( h \) in funzione di \( r \)
Il volume totale è dato dalla somma dei due volumi:
\[ V = \pi r^2 h + \frac{2}{3}\pi r^3 \]
Isoliamo il termine con la \( h \):
\[ \pi r^2 h = V - \frac{2}{3}\pi r^3 \]
Dividiamo tutto per \( \pi r^2 \) per trovare \( h \):
\[ h = \frac{V - \frac{2}{3}\pi r^3}{\pi r^2} = \frac{V}{\pi r^2} - \frac{\frac{2}{3}\pi r^3}{\pi r^2} \]
\[ h = \frac{V}{\pi r^2} - \frac{2}{3}r \]
3. Costruzione della funzione Superficie \( S(r) \)
La superficie totale è la somma della base, della superficie laterale del cilindro e della cupola sferica:
\[ S = \pi r^2 + 2\pi r h + 2\pi r^2 = 3\pi r^2 + 2\pi r h \]
Sostituiamo l'espressione di \( h \) trovata al punto precedente:
\[ S(r) = 3\pi r^2 + 2\pi r \left( \frac{V}{\pi r^2} - \frac{2}{3}r \right) \]
Sviluppiamo il prodotto nella parentesi:
\[ S(r) = 3\pi r^2 + \frac{2\pi r V}{\pi r^2} - \frac{4\pi r^2}{3} \]
Semplifichiamo i termini e mettiamo a comune denominatore \( 3\pi r^2 \) e \( \frac{4}{3}\pi r^2 \):
\[ S(r) = \frac{2V}{r} + \left( 3 - \frac{4}{3} \right) \pi r^2 = \frac{2V}{r} + \left( \frac{9-4}{3} \right) \pi r^2 \]
\[ S(r) = \frac{2V}{r} + \frac{5}{3}\pi r^2 \]
4. Ricerca del minimo e studio del segno
Calcoliamo la derivata di \( S(r) \):
\[ S'(r) = -\frac{2V}{r^2} + \frac{10}{3}\pi r \]
Poniamo la derivata uguale a zero per trovare il punto critico:
\[ \frac{10\pi r}{3} = \frac{2V}{r^2} \Rightarrow 10\pi r^3 = 6V \Rightarrow r^3 = \frac{6V}{10\pi} = \frac{3V}{5\pi} \]
Studio algebrico del segno di \( S'(r) \):
Mettiamo la derivata a comune denominatore:
\[ S'(r) = \frac{-6V + 10\pi r^3}{3r^2} \]
Poiché il denominatore \( 3r^2 \) è sempre positivo per \( r > 0 \), studiamo solo il numeratore:
- \( 10\pi r^3 - 6V > 0 \Rightarrow r^3 > \frac{3V}{5\pi} \Rightarrow r > \sqrt[3]{\frac{3V}{5\pi}} \) (Funzione crescente)
- \( 10\pi r^3 - 6V < 0 \Rightarrow r < \sqrt[3]{\frac{3V}{5\pi}} \) (Funzione decrescente)
Questo conferma che in \( r = \sqrt[3]{\frac{3V}{5\pi}} \) abbiamo un minimo assoluto.
5. Calcolo finale dell'altezza e Risultato
Riprendiamo la formula di \( h \) e sostituiamo il valore di \( V \) ricavato dalla condizione di minimo \( 6V = 10\pi r^3 \Rightarrow V = \frac{5}{3}\pi r^3 \):
\[ h = \frac{\frac{5}{3}\pi r^3}{\pi r^2} - \frac{2}{3}r = \frac{5}{3}r - \frac{2}{3}r = \frac{3}{3}r = r \]
Conclusione: \( h = r \)
Il solido ottimale ha l'altezza del cilindro uguale al raggio della base.
Soluzione Esercizio 3
a) Dimostrazione di non invertibilità
1. Studio della Parità (Simmetria):
Sostituiamo \( x \) con \( -x \) nella funzione:
\[ f(-x) = \frac{e^{2(-x)^2}}{(-x)^2 + 2} = \frac{e^{2x^2}}{x^2 + 2} = f(x) \]
La funzione è pari: questo significa che il grafico è simmetrico rispetto all'asse \( y \). Ad esempio, \( f(1) \) e \( f(-1) \) danno lo stesso risultato. Poiché due valori diversi di \( x \) hanno la stessa immagine, la funzione non è iniettiva e quindi non è invertibile nel dominio \( \mathbb{R} \).
2. Calcolo della derivata prima:
Usiamo la regola del quoziente \( \left(\frac{N}{D}\right)' = \frac{N'D - ND'}{D^2} \):
- Numeratore \( N = e^{2x^2} \rightarrow N' = 4xe^{2x^2} \)
- Denominatore \( D = x^2 + 2 \rightarrow D' = 2x \)
\[ f'(x) = \frac{(4xe^{2x^2})(x^2+2) - (e^{2x^2})(2x)}{(x^2+2)^2} \]
Raccogliamo \( 2xe^{2x^2} \) al numeratore:
\[ f'(x) = \frac{2xe^{2x^2} [2(x^2+2) - 1]}{(x^2+2)^2} = \frac{2xe^{2x^2} (2x^2+3)}{(x^2+2)^2} \]
b) Invertibilità nell'intervallo \( I = (-\infty, 0] \)
Analizziamo il segno della derivata \( f'(x) \):
- I termini \( e^{2x^2} \), \( (2x^2+3) \) e \( (x^2+2)^2 \) sono sempre positivi.
- Il segno della derivata dipende solo dal fattore \( 2x \).
Nell'intervallo \( (-\infty, 0] \), la \( x \) è negativa o nulla, quindi \( f'(x) \le 0 \).
Essendo la funzione strettamente decrescente in questo intervallo, essa è iniettiva e dunque invertibile.
c) Calcolo della derivata dell'inversa
Dobbiamo calcolare \( g'(y_0) \) con \( y_0 = \frac{e^2}{3} \). La formula è:
\[ g'(y_0) = \frac{1}{f'(x_0)} \]
1. Troviamo \( x_0 \):
Cerchiamo quel valore \( x \in (-\infty, 0] \) tale che \( f(x) = \frac{e^2}{3} \):
\[ \frac{e^{2x^2}}{x^2+2} = \frac{e^2}{3} \Rightarrow \text{per tentativi diretti: } x_0 = -1 \]
2. Calcoliamo \( f'(-1) \):
\[ f'(-1) = \frac{2(-1)e^{2(1)}(2(1)+3)}{(1+2)^2} = -\frac{10e^2}{9} \]
3. Risultato finale:
\[ g'\left(\frac{e^2}{3}\right) = \frac{1}{-\frac{10e^2}{9}} = -\frac{9}{10e^2} \]
Nota Finale: Monotonia e Invertibilità
Abbiamo osservato che la monotonia è una condizione sufficiente per l'invertibilità, ma non necessaria.
Si consideri, ad esempio, la funzione \( f(x) \) definita a tratti:
\[ f(x)= \begin{cases} x & \text{se } 0 \le x < 1 \\ -x+3.5 & \text{se } 1 \le x \le 2.5 \end{cases} \]
Questa funzione è definita nell'intervallo chiuso \( [0, 2.5] \) e ha come immagine \( [0, 2.5] \).
Il suo grafico dimostra chiaramente che la funzione NON È MONOTONA su tutto il dominio, eppure è INIETTIVA (ogni valore \( y \) è raggiunto una sola volta). Di conseguenza, la funzione È INVERTIBILE.
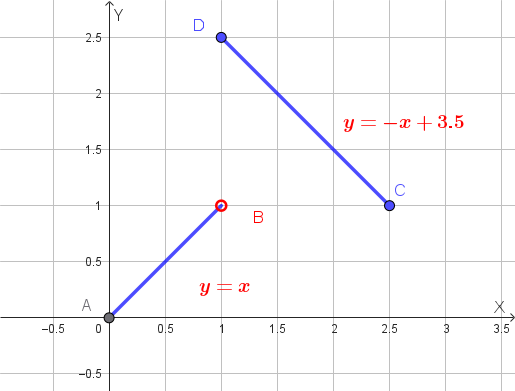
Grafico della funzione a tratti: iniettiva ma non monotona





