📚 Disponibile anche in versione DSA
Questo compito è stato assegnato il 20 Novembre 1989 a una classe 5ª del Liceo Scientifico.
Argomenti: calcolo di una primitiva, studio di funzione, grafico del logaritmo naturale di una funzione. Soluzione approssimata di un'equazione (metodo di bisezione e delle tangenti). Problema di minimo con geometria solida, invertibilità di una funzione,
derivata in un punto della funzione inversa.
Considera la funzione di equazione \( g(x) = 3x^2 + 2x + a \) (con \( a \) parametro reale).
a) Tra tutte le primitive di \( g(x) \) determina quella che ha come tangente inflessionale la retta di equazione \( y = -4x - 4 \) e indicala con \( y = f(x) \).
b) Studia la curva di equazione \( y = f(x) \) e rappresentala graficamente indicando il valore approssimato a meno di un decimo dell’ascissa del punto di intersezione con l’asse delle ascisse.
c) Deduci dal grafico di \( y = f(x) \) il grafico di \( y = \ln f(x) \).
Primitive della funzione \( g(x) \)
\[ f(x)=\int(3x^2+2x+a)\,dx =x^3+x^2+ax+c \]
Derivate
Punto di flesso (che esiste ed è unico trattandosi di una cubica)
\[ f''(x)=0 \Rightarrow 6x+2=0 \Rightarrow x_f=-\frac13 \]
Condizione sulla tangente inflessionale
La retta tangente inflessionale ha coefficiente angolare \( m=-4 \), quindi:
\[ f'\!\left(-\frac13\right)=-4 \] \[ 3\cdot\frac{1}{9}-\frac{2}{3}+a=-4 \Rightarrow -\frac13+a=-4 \Rightarrow a=-1 \]
Determinazione della costante \( c \)
Il punto di flesso deve appartenere alla retta \( y=-4x-4 \).
\[ f\!\left(-\frac13\right) =-\frac{1}{27}+\frac{1}{9}+\frac{1}{3}+c =\frac{11}{27}+c \] \[ y=-4\left(-\frac13\right)-4=-\frac83 \] \[ \frac{11}{27}+c=-\frac83 \Rightarrow c=-4 \]
Dominio
\( D=\mathbb{R} \)
Intersezioni con gli assi
Metodo di bisezione
\[ f(1)=-3 \quad,\quad f(2)=6 \Rightarrow \alpha\in(1,2) \]
| Iter. | a | b | c | f(c) |
|---|---|---|---|---|
| 1 | 1,00 | 2,00 | 1,50 | +0,125 |
| 2 | 1,00 | 1,50 | 1,25 | -2,109 |
| 3 | 1,25 | 1,50 | 1,375 | -1,060 |
| 4 | 1,375 | 1,50 | 1,4375 | -0,492 |
| 5 | 1,4375 | 1,50 | 1,46875 | -0,194 |
| 6 | 1,46875 | 1,50 | 1,484375 | -0,032 |
| 7 | 1,484375 | 1,50 | 1,4921875 | +0,052 |
\[ \Rightarrow \alpha \approx 1{,}49 \]
Metodo delle tangenti (Newton)
La radice dell’equazione \( f(x)=0 \) appartiene all’intervallo \( (1,2) \), poiché \( f(1) < 0 \) e \( f(2) > 0 \). In tale intervallo risulta:
\[ f''(x)=6x+2>0 \quad \text{per ogni } x\in(1,2) \]
Scegliamo quindi come punto iniziale \( x_0=1{,}5 \), che appartiene all’intervallo e per il quale:
\[ f(1{,}5)=0{,}125>0 \]
Poiché \( f(1{,}5) \) ha lo stesso segno di \( f''(x) \), la scelta di \( x_0=1{,}5 \) garantisce la convergenza del metodo delle tangenti.
\[ x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)},\quad f'(x)=3x^2+2x-1 \]
\[ x_0=1{,}5 \Rightarrow x_1=1{,}5-\frac{0{,}125}{8{,}75}=1{,}4857 \] \[ f(1{,}4857)\approx -0{,}0036 \qquad f'(1{,}4857)\approx 8{,}69 \] \[ x_2=1{,}4857-\frac{-0{,}0036}{8{,}69}\approx1{,}4861 \Rightarrow \alpha\approx1{,}49 \]
Derivata prima e monotonia
\[ f'(x)=3x^2+2x-1 \Rightarrow x=-1,\;\frac13 \]
Indichiamo con \( \alpha \) la radice reale dell’equazione \( f(x)=0 \), con \( \alpha\in(1,2) \) e \( \alpha\approx1{,}49 \).
La funzione interseca l’asse delle ascisse nel punto \( (\alpha,0) \).
\[ f(-1)=-3 \quad (\text{massimo relativo}) \] \[ f\!\left(\frac13\right)=-\frac{113}{27} \approx -4{,}19 \quad (\text{minimo relativo}) \]
Derivata seconda e concavità
\[ f''(x)=6x+2 \Rightarrow x=-\frac13 \] \[ f\!\left(-\frac13\right)=-\frac{97}{27}\approx-3{,}59 \]
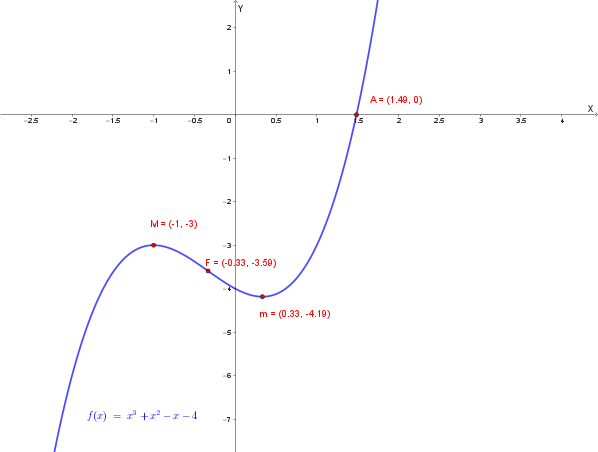
Grafico di \( y=f(x)=x^3+x^2-x-4 \)
Dominio
\[ f(x)>0 \Rightarrow x>\alpha \]
dove \( \alpha \) è l’unica radice reale dell’equazione \( f(x)=0 \), con \( \alpha\in(1,2) \) e \( \alpha\approx1{,}49 \).
Asintoto verticale
\[ \lim_{x\to\alpha^+}\ln f(x)=-\infty \]
Monotonia
\[ (\ln f(x))'=\frac{f'(x)}{f(x)}>0 \quad \text{per ogni } x>\alpha \]
Dallo studio di \( f(x) \) risulta che, per \( x\to+\infty \), si ha \( f(x)\to+\infty \); di conseguenza \[ \ln f(x)\to+\infty. \]
Inoltre, non esiste asintoto obliquo per il grafico di \( y=\ln f(x) \), poiché, per \( x\to+\infty \), risulta \( f(x)\sim x^3 \) (con \( x>0 \)) e quindi: \[ \ln f(x)\sim \ln(x^3)=3\ln x. \]
\[ \lim_{x\to+\infty}\frac{\ln f(x)}{x} =\lim_{x\to+\infty}\frac{3\ln x}{x}=0, \]
poiché \( x \) è un infinito di ordine superiore rispetto a \( \ln x \) per \( x\to+\infty \).
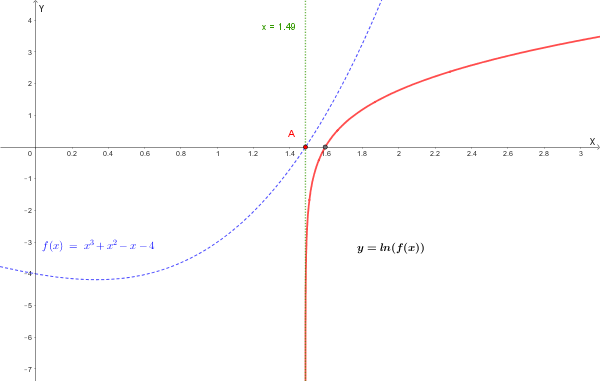
Grafico di \( y=\ln f(x) \)
Tra tutti i solidi di volume assegnato \( V \), costituiti da un cilindro al quale è sovrapposta una semisfera con la base coincidente con la base del cilindro, determinare quello che ha superficie totale minima.
Problema: Determinare le dimensioni del solido (cilindro + semisfera) con volume \( V \) assegnato che minimizza la superficie totale.
Sia:
Figura
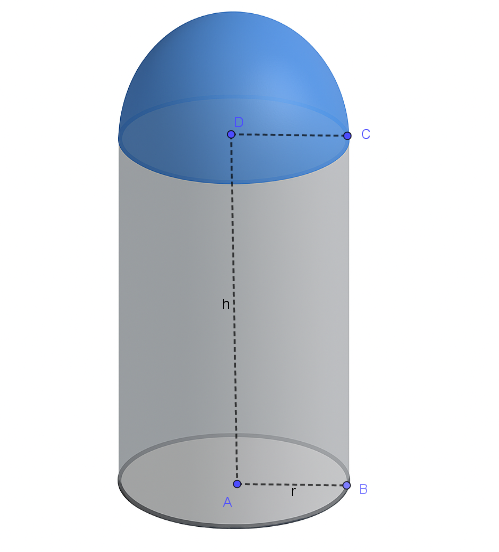
Cilindro e semisfera sovrapposta
Volume del cilindro:
\[ V_{\text{cilindro}} = \pi r^2 h \]
Volume della semisfera:
\[ V_{\text{semisfera}} = \frac{1}{2} \cdot \frac{4}{3}\pi r^3 = \frac{2}{3}\pi r^3 \]
Volume totale:
\[ V = V_{\text{cilindro}} + V_{\text{semisfera}} = \pi r^2 h + \frac{2}{3}\pi r^3 \]
Da questa equazione ricaviamo \( h \) in funzione di \( r \):
\[ \pi r^2 h = V - \frac{2}{3}\pi r^3 \]
\[ h = \frac{V}{\pi r^2} - \frac{2r}{3} \]
La superficie totale del solido è composta da:
Superficie totale:
\[ S = 2\pi r h + \pi r^2 + 2\pi r^2 = 2\pi r h + 3\pi r^2 \]
Sostituendo l'espressione di \( h \):
\[ S(r) = 2\pi r \left(\frac{V}{\pi r^2} - \frac{2r}{3}\right) + 3\pi r^2 \]
\[ S(r) = \frac{2V}{r} - \frac{4\pi r^2}{3} + 3\pi r^2 \]
\[ S(r) = \frac{2V}{r} + 3\pi r^2 - \frac{4\pi r^2}{3} \]
\[ S(r) = \frac{2V}{r} + \pi r^2\left(3 - \frac{4}{3}\right) \]
\[ S(r) = \frac{2V}{r} + \frac{5\pi r^2}{3} \]
Per trovare il valore di \( r \) che minimizza \( S(r) \), calcoliamo la derivata prima:
\[ S'(r) = -\frac{2V}{r^2} + \frac{10\pi r}{3} \]
Poniamo \( S'(r) = 0 \):
\[ -\frac{2V}{r^2} + \frac{10\pi r}{3} = 0 \]
\[ \frac{10\pi r}{3} = \frac{2V}{r^2} \]
\[ 10\pi r^3 = 6V \]
\[ r^3 = \frac{6V}{10\pi} = \frac{3V}{5\pi} \]
Raggio ottimale: \[ r = \sqrt[3]{\frac{3V}{5\pi}} \]
Calcoliamo la derivata seconda:
\[ S''(r) = \frac{4V}{r^3} + \frac{10\pi}{3} \]
Per \( r > 0 \) e \( V > 0 \), entrambi i termini sono positivi, quindi:
\[ S''(r) > 0 \quad \forall r > 0 \]
Conclusione: Il punto critico trovato è effettivamente un minimo.
Metodo alternativo: Studio del segno della derivata prima
Studiamo il segno di \( S'(r) = -\frac{2V}{r^2} + \frac{10\pi r}{3} \) per \( r > 0 \):
\[ S'(r) = \frac{10\pi r^3 - 6V}{3r^2} \]
Il denominatore \( 3r^2 > 0 \) sempre per \( r > 0 \), quindi il segno dipende dal numeratore:
Schema dei segni:
| \( r \) | 0 | \( \sqrt[3]{\frac{3V}{5\pi}} \) | \( +\infty \) | ||
| \( S'(r) \) | − | 0 | + | ||
| \( S(r) \) | ↘ | MIN | ↗ |
La funzione \( S(r) \) è decrescente per \( r <\sqrt[3]{\frac{3V}{5\pi}} \) e crescente per \( r > \sqrt[3]{\frac{3V}{5\pi}} \), quindi \( r = \sqrt[3]{\frac{3V}{5\pi}} \) è un punto di minimo assoluto.
Sostituiamo il valore ottimale di \( r \) nell'espressione di \( h \):
\[ h = \frac{V}{\pi r^2} - \frac{2r}{3} \]
Con \( r^3 = \frac{3V}{5\pi} \), otteniamo \( r^2 = \left(\frac{3V}{5\pi}\right)^{2/3} \):
\[ h = \frac{V}{\pi \left(\frac{3V}{5\pi}\right)^{2/3}} - \frac{2}{3}\left(\frac{3V}{5\pi}\right)^{1/3} \]
Semplificando (calcolo laborioso):
\[ h = \frac{V}{\pi r^2} - \frac{2r}{3} = \frac{3V}{5\pi r^2} - \frac{2r}{3} \]
Dato che \( r^3 = \frac{3V}{5\pi} \), possiamo scrivere \( V = \frac{5\pi r^3}{3} \):
\[ h = \frac{5\pi r^3}{3 \cdot \pi r^2} - \frac{2r}{3} = \frac{5r}{3} - \frac{2r}{3} = \frac{3r}{3} = r \]
Altezza ottimale: \[ h = r \]
Il solido con superficie totale minima, a volume \( V \) assegnato, ha le seguenti dimensioni:
Raggio:
\[ r = \sqrt[3]{\frac{3V}{5\pi}} \]
Altezza del cilindro:
\[ h = r = \sqrt[3]{\frac{3V}{5\pi}} \]
Relazione notevole:
\[ \boxed{h = r} \]
L'altezza del cilindro è uguale al raggio!
Osservazione geometrica:
Questa condizione \( h = r \) è una proprietà elegante del problema di ottimizzazione: il solido ottimale ha il cilindro con altezza uguale al raggio della base. Il diametro della base è quindi \( 2r = 2h \), cioè il doppio dell'altezza del cilindro.
Si consideri la funzione di equazione:
\[ y = f(x) = \frac{e^{2x^2}}{x^2 + 2} \]
a) Dimostrare che la funzione non è invertibile in tutto il suo dominio.
b) Verificare che è invertibile nell'intervallo \( I=(-\infty, 0] \).
c) Detta \( g \) la funzione inversa di \( f \) in \( I \), calcolare \( g'\left(\frac{e^2}{3}\right) \).
La funzione da studiare è:
\[ y = f(x) = \frac{e^{2x^2}}{x^2 + 2} \]
1. Dominio: \( D = (-\infty, +\infty) = \mathbb{R} \).
2. Calcolo della derivata prima \( f'(x) \):
Utilizziamo la regola di derivazione del quoziente: \( \left(\frac{A}{B}\right)' = \frac{A'B - AB'}{B^2} \). Sia \( A = e^{2x^2} \) e \( B = x^2 + 2 \).
Derivata del numeratore: \( A' = \frac{d}{dx}(e^{2x^2}) = e^{2x^2} \cdot \frac{d}{dx}(2x^2) = 4xe^{2x^2} \)
Derivata del denominatore: \( B' = \frac{d}{dx}(x^2 + 2) = 2x \)
Applichiamo la formula del quoziente:
\[ f'(x) = \frac{(4xe^{2x^2}) (x^2 + 2) - (e^{2x^2}) (2x)}{(x^2 + 2)^2} \]
Raccogliamo il termine comune \( 2xe^{2x^2} \) al numeratore:
\[ f'(x) = \frac{2xe^{2x^2} [2(x^2 + 2) - 1]}{(x^2 + 2)^2} \]
Semplifichiamo l'espressione tra parentesi quadre:
\[ 2(x^2 + 2) - 1 = 2x^2 + 4 - 1 = 2x^2 + 3 \]
Quindi, la derivata prima è:
\[ f'(x) = \frac{2xe^{2x^2} (2x^2 + 3)}{(x^2 + 2)^2} \]
3. Studio del segno di \( f'(x) \) e Monotonia:
Notiamo che il segno della derivata prima dipende dal segno d \(x\). Quindi:
\( f'(x) < 0 \) se \( x < 0 \) (funzione **decrescente**)
\( f'(x) > 0 \) se \( x > 0 \) (funzione **crescente**)
4. Deduzione della non invertibilità (Iniettività):
La funzione non è strettamente monotona in tutto \( \mathbb{R} \). Sebbene la **monotonia** sia una condizione **sufficiente** per l'invertibilità, essa **non è necessaria** (vedi nota finale). Pertanto, la sola non-monotonia non basta a concludere la non-invertibilità.
Tuttavia, verifichiamo la simmetria della funzione:
\[ f(-x) = \frac{e^{2(-x)^2}}{(-x)^2 + 2} = \frac{e^{2x^2}}{x^2 + 2} = f(x) \]
Poiché \( f(-x) = f(x) \), la funzione \( f(x) \) è **pari** e il suo grafico è **simmetrico rispetto all'asse delle ordinate** (\(y\)).
Questo implica che, per ogni \( x \neq 0 \), esiste un \( -x \neq x \) tale che \( f(-x) = f(x) \). La funzione **non è iniettiva** e, di conseguenza, **non è invertibile** in tutto il suo dominio \( \mathbb{R} \).
Nell'intervallo \( I=(-\infty, 0] \), la funzione è **strettamente decrescente** (\( f'(x) < 0 \) per \( x < 0 \)). Una funzione strettamente monotona è iniettiva e quindi è **invertibile** nell'intervallo \( I \). Sia \( g \) la funzione inversa di \( f \) in questo intervallo.
Per calcolare la derivata della funzione inversa \( g'(y_0) \), utilizziamo il teorema sulla derivata della funzione inversa:
\[ g'(y_0) = \frac{1}{f'(x_0)} \quad \text{dove } y_0 = f(x_0) \]
Conosciamo \( y_0 = \frac{e^2}{3} \). Troviamo \( x_0 \in I=(-\infty, 0] \) risolvendo \( f(x_0) = \frac{e^2}{3} \). Si trova \( x_0 = -1 \).
Calcolo di \( f'(x_0) = f'(-1) \):
\[ f'(-1) = \frac{2(-1)e^{2} (2(1) + 3)}{(1 + 2)^2} = -\frac{10e^2}{9} \]
Calcolo di \( g'\left(\frac{e^2}{3}\right) \):
\[ g'\left(\frac{e^2}{3}\right) = \frac{1}{f'(-1)} = \frac{1}{-\frac{10e^2}{9}} \] \[ g'\left(\frac{e^2}{3}\right) = -\frac{9}{10e^2} \]
Abbiamo osservato che la **monotonia** è una condizione **sufficiente** per l'invertibilità di una funzione, ma **non necessaria**.
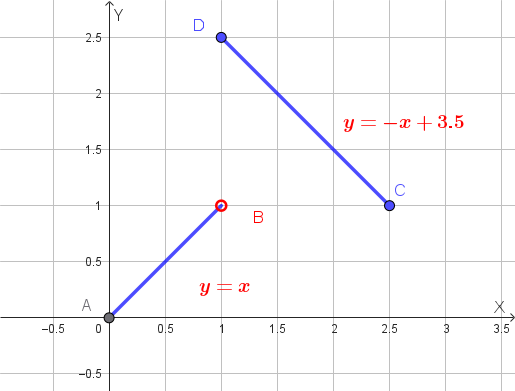
Si consideri, ad esempio, la funzione \( f(x) \) definita a tratti:
\[ f(x)= \begin{cases} x & \text{se } 0 \le x < 1 \\ -x+3.5 & \text{se } 1 \le x \le 2.5 \end{cases} \]
Questa funzione è definita nell'intervallo chiuso \( [0, 2.5] \) e ha come immagine \( [0, 2.5] \). Il suo grafico dimostra chiaramente che la funzione **NON È MONOTONA** su tutto il dominio, eppure è **INIETTIVA** (ogni valore \( y \) è raggiunto una sola volta). Di conseguenza, la funzione **È INVERTIBILE**.