



Questo compito è stato assegnato il giorno 16 Novembre 2010 a una classe 5ª del Liceo Scientifico.
Argomenti: calcolo di limiti, grafico qualitativo di una funzione, dal grafico di una funzione al grafico del logaritmo della funzione, continuità di una funzione, classificazione dei punti di discontinuità, ordine di infinitesimo, Teorema degli zeri.
Tracciare un grafico qualitativo della funzione di equazione \(y = \frac{x^2 - 4}{x^3}\).
Per tracciare il grafico qualitativo di \(y = \frac{x^2 - 4}{x^3}\), analizziamo i seguenti aspetti:
Numeratore: \(x^2 - 4 > 0 \implies x^2 > 4 \implies x < -2 \text{ o } x > 2\)
Denominatore: \(x^3 > 0 \implies x > 0\)
Tabella dei segni:
| Intervallo | \(x^2 - 4\) | \(x^3\) | \(f(x)\) |
|---|---|---|---|
| \(x < -2\) | + | - | - |
| \(-2 < x < 0\) | - | - | + |
| \(0 < x < 2\) | - | + | - |
| \(x > 2\) | + | + | + |
La funzione è positiva per \(-2 < x < 0\) e per \(x > 2\).
La funzione è negativa per \(x < -2\) e per \(0 < x < 2\).
Considerando zeri, asintoti e il segno della funzione, possiamo tracciare un grafico qualitativo:
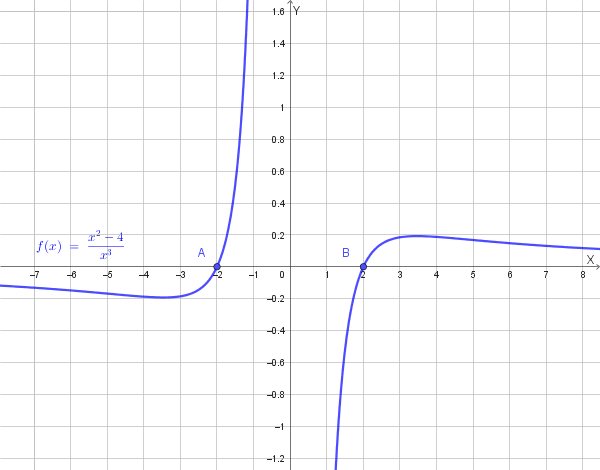
La funzione di equazione y = f(x), definita su tutto l’asse reale, ha il seguente grafico:
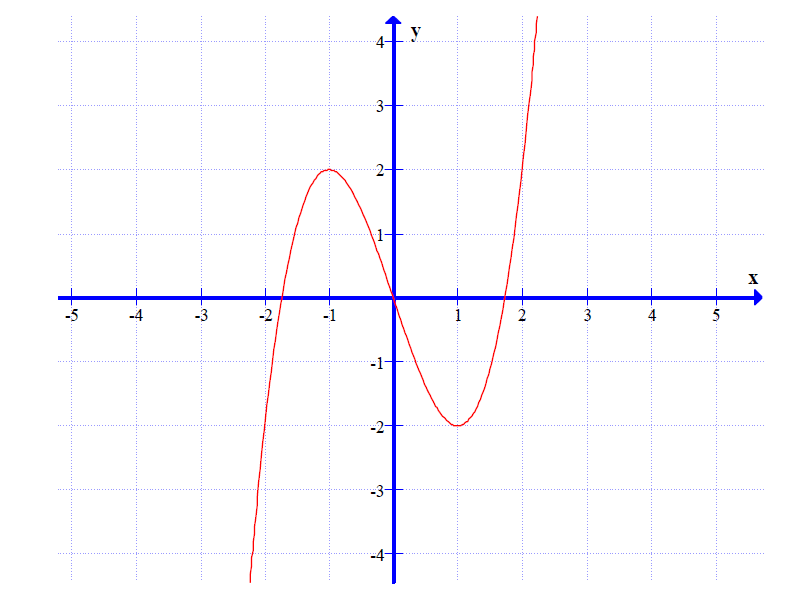
Dedurre il grafico qualitativo della funzione di equazione \( y = ln f(x) \).
Dobbiamo dedurre dal grafico di \(y=f(x)\) dato il grafico qualitativo di \(y=\ln f(x)\).
Deve essere \(f(x) > 0\). Dal grafico fornito osserviamo che \(f(x) > 0\) per \(-a < x < 0\) e per \(x > a\), con \(1 < a < 2\).
Quindi il dominio di \(y=\ln f(x)\) è: \(-a < x < 0\) oppure \(x > a\).
Dal grafico di \(y=f(x)\) deduciamo che \(f(x)\) è **dispari**, in quanto il suo grafico è simmetrico rispetto all'origine degli assi cartesiani. Quindi \(f(-x)=-f(x)\). Risulta:
\(\ln f(-x) = \ln (-f(x))\), che non esiste, perché \(-f(x) < 0\) nel dominio di \(\ln f(x)\).
La funzione \(y=\ln f(x)\) **non è pari né dispari** (non ha un grafico simmetrico rispetto all'asse delle ordinate o rispetto all'origine degli assi).
Risulta \(\ln f(x) > 0\) dove \(f(x) > 1\). Ed in base a quanto detto sulle intersezioni con l'asse delle x, ciò avviene per \(b < x < c\) e \(x > d\).
Ricordiamo che il dominio è \(-a < x < 0 \cup x > a\), con \(1 < a < 2\).
Quindi \(x=-a\) è un **asintoto verticale**.
Quindi \(x=0\) è un **asintoto verticale**.
Quindi \(x=a\) è un **asintoto verticale**.
Limite per \(x \to +\infty\): \(\lim_{x \to +\infty} \ln f(x) = \ln(+\infty) = +\infty\).
Non c'è un asintoto orizzontale. Potrebbe esserci un asintoto obliquo, ma ci è richiesto solo un grafico qualitativo.
Il grafico qualitativo della funzione \(y=\ln f(x)\) è il seguente (grafico in blu):

Calcolare i seguenti limiti:
a) \(\lim_{x \to +\infty} (\sqrt{x^2+4x} - \sqrt{x^2-3})\)
b) \(\lim_{x \to 0} \frac{x^2}{1-\cos 3x}\)
Questo limite si presenta nella forma indeterminata \(\infty - \infty\). Per risolverlo, moltiplichiamo e dividiamo per lo stesso fattore:
\[ \lim_{x \to +\infty} (\sqrt{x^2+4x} - \sqrt{x^2-3}) = \lim_{x \to +\infty} (\sqrt{x^2+4x} - \sqrt{x^2-3}) \cdot \frac{\sqrt{x^2+4x} + \sqrt{x^2-3}}{\sqrt{x^2+4x} + \sqrt{x^2-3}} \] \[ = \lim_{x \to +\infty} \frac{(x^2+4x) - (x^2-3)}{\sqrt{x^2+4x} + \sqrt{x^2-3}} \] \[ = \lim_{x \to +\infty} \frac{4x+3}{\sqrt{x^2(1+4/x)} + \sqrt{x^2(1-3/x^2)}} \]Per \(x \to +\infty\), \(\sqrt{x^2} = |x| = x\).
\[ = \lim_{x \to +\infty} \frac{4x+3}{x\sqrt{1+4/x} + x\sqrt{1-3/x^2}} \] \[ = \lim_{x \to +\infty} \frac{x(4+3/x)}{x(\sqrt{1+4/x} + \sqrt{1-3/x^2})} \] \[ = \lim_{x \to +\infty} \frac{4+3/x}{\sqrt{1+4/x} + \sqrt{1-3/x^2}} \]Sostituendo il limite:
\[ = \frac{4+0}{\sqrt{1+0} + \sqrt{1-0}} = \frac{4}{1+1} = \frac{4}{2} = 2 \]Quindi, \(\lim_{x \to +\infty} (\sqrt{x^2+4x} - \sqrt{x^2-3}) = 2\).
Questo limite si presenta nella forma indeterminata \(\frac{0}{0}\). Possiamo utilizzare i limiti notevoli.
Ricordiamo il limite notevole: \(\lim_{t \to 0} \frac{1-\cos t}{t^2} = \frac{1}{2}\).
Nel nostro caso, abbiamo \(1-\cos 3x\). Per applicare il limite notevole, dobbiamo avere \((3x)^2\) al denominatore.
\[ \lim_{x \to 0} \frac{x^2}{1-\cos 3x} = \lim_{x \to 0} \frac{x^2}{\frac{1-\cos 3x}{(3x)^2} \cdot (3x)^2} \] \[ = \lim_{x \to 0} \frac{x^2}{\frac{1-\cos 3x}{(3x)^2} \cdot 9x^2} \] \[ = \lim_{x \to 0} \frac{1}{9 \cdot \frac{1-\cos 3x}{(3x)^2}} \]Poiché \(\lim_{x \to 0} \frac{1-\cos 3x}{(3x)^2} = \frac{1}{2}\), abbiamo:
\[ = \frac{1}{9 \cdot \frac{1}{2}} = \frac{1}{9/2} = \frac{2}{9} \]Quindi, \(\lim_{x \to 0} \frac{x^2}{1-\cos 3x} = \frac{2}{9}\).
Classificare i punti di discontinuità della funzione di equazione:
\(y=\frac{(e^{x-1}-1) \sin x}{x^2-x^3}\)
La funzione è \(f(x) = \frac{(e^{x-1}-1) \sin x}{x^2-x^3}\).
Il dominio della funzione è dato dalle condizioni per cui il denominatore non sia nullo:
\[ x^2 - x^3 \neq 0 \] \[ x^2(1 - x) \neq 0 \]Quindi, i punti in cui la funzione non è definita sono \(x=0\) e \(x=1\).
Analizziamo i limiti in questi punti per classificare le discontinuità.
Calcoliamo il limite per \(x \to 0\):
\[ \lim_{x \to 0} \frac{(e^{x-1}-1) \sin x}{x^2(1-x)} \]Per \(x \to 0\), abbiamo:
Sostituiamo gli sviluppi asintotici:
\[ \lim_{x \to 0} \frac{(\frac{1}{e}-1) \cdot x}{x^2 \cdot 1} = \lim_{x \to 0} \frac{(\frac{1}{e}-1)}{x} \]Poiché il limite tende a infinito, il punto \(x=0\) è un **punto di discontinuità di seconda specie**.
Calcoliamo il limite per \(x \to 1\):
\[ \lim_{x \to 1} \frac{(e^{x-1}-1) \sin x}{x^2(1-x)} \]Per \(x \to 1\):
Sostituiamo gli sviluppi asintotici e i valori a cui tendono i fattori:
\[ \lim_{x \to 1} \frac{(x-1) \sin 1}{1 \cdot (1-x)} = \lim_{x \to 1} \frac{(x-1) \sin 1}{-(x-1)} \] \[ = \lim_{x \to 1} (-\sin 1) = -\sin 1 \]Dato che il limite esiste finito (\(-\sin 1 \approx -0.841\)), il punto \(x=1\) è un **punto di discontinuità di terza specie (eliminabile)**.
La funzione può essere resa continua in \(x=1\) definendo \(f(1) = -\sin 1\).
È vero che
\[ \lim_{x \to 0} x^2 \cos\left(\frac{1}{x}\right)=0 \]
Motivare la risposta.
Sì, l'affermazione è vera. Per dimostrarlo, possiamo utilizzare il Teorema del Confronto (detto "dei due Carabinieri").
Sappiamo che la funzione coseno è limitata, ovvero:
\[ -1 \le \cos\left(\frac{1}{x}\right) \le 1 \]Moltiplicando tutti i membri della disuguaglianza per \(x^2\), che è sempre non negativo (\(x^2 \ge 0\)), le disuguaglianze mantengono il loro verso:
\[ -x^2 \le x^2 \cos\left(\frac{1}{x}\right) \le x^2 \]Ora calcoliamo il limite per \(x \to 0\) delle due funzioni estreme:
\[ \lim_{x \to 0} (-x^2) = 0 \] \[ \lim_{x \to 0} (x^2) = 0 \]Poiché i limiti delle due funzioni esterne sono entrambi uguali a \(0\), per il Teorema del Confronto, anche il limite della funzione data è \(0\).
\[ \lim_{x \to 0} x^2 \cos\left(\frac{1}{x}\right)=0 \]Questo dimostra che il limite è effettivamente \(0\).
Sapendo che \(f(x)=(1-\cos x)\ln\sqrt{1+x}\), determinare la **parte principale** e l’**ordine di infinitesimo** di \(f(x)\), per \(x \to 0\), rispetto all’infinitesimo campione \(y = x\).
La funzione data è \(f(x)=(1-\cos x)\ln\sqrt{1+x}\).
Dobbiamo determinare la parte principale e l'ordine di infinitesimo di \(f(x)\) per \(x \to 0\), rispetto all'infinitesimo campione \(y=x\).
Utilizziamo gli **sviluppi asintotici** (o limiti notevoli) per \(x \to 0\):
Ora sostituiamo questi sviluppi nella funzione \(f(x)\):
\[ f(x) = (1-\cos x)\ln\sqrt{1+x} \] \[ f(x) \sim \left(\frac{1}{2}x^2\right) \cdot \left(\frac{1}{2}x\right) \] \[ f(x) \sim \frac{1}{4}x^3 \]La **parte principale** di \(f(x)\) per \(x \to 0\) è \(\frac{1}{4}x^3\).
L'**ordine di infinitesimo** di \(f(x)\) per \(x \to 0\), rispetto all'infinitesimo campione \(y=x\), è l'esponente di \(x\) nella sua parte principale. In questo caso, l'ordine è **3**.
Siano \(f(x)\) e \(g(x)\) due infinitesimi per \(x \to x_0\) (con \(x_0\) finito o infinito), cioè \(\lim_{x \to x_0} f(x) = 0\) e \(\lim_{x \to x_0} g(x) = 0\).
Si dice che \(f(x)\) è un infinitesimo di **ordine \(k\)** rispetto all'infinitesimo campione \(g(x)\) se esiste finito e non nullo il limite:
\[ \lim_{x \to x_0} \frac{f(x)}{|g(x)|^k} = L \neq 0 \]La **parte principale** di \(f(x)\) rispetto a \(g(x)\) è l'espressione \(L \cdot |g(x)|^k\).
Nel nostro caso, l'infinitesimo campione è \(g(x) = x\), quindi cerchiamo un \(k\) tale che \(\lim_{x \to 0} \frac{f(x)}{|x|^k} = L \neq 0\). La parte principale sarà \(L |x|^k\).
a) Servendosi del “Teorema degli zeri” dimostrare che la seguente equazione ammette almeno una radice nell’intervallo [2;3]:
\[ \ln(x - 1) + x - 3 = 0 \]
b) Dimostrare che tale radice è unica.
c) Calcolare il valore approssimato a meno di un decimo della suddetta radice utilizzando il metodo grafico ed una tabulazione dei valori.
Consideriamo la funzione \(f(x) = \ln(x - 1) + x - 3\).
Per applicare il Teorema degli Zeri nell'intervallo \([2;3]\), dobbiamo verificare due condizioni:
Abbiamo \(f(2) = -1 < 0\) e \(f(3) = \ln(2) > 0\). Poiché \(f(2)\) e \(f(3)\) hanno segni opposti, per il **Teorema degli Zeri**, esiste almeno una radice (uno zero) dell'equazione \(\ln(x - 1) + x - 3 = 0\) nell'intervallo aperto \((2;3)\).
Risolvere l'equazione \(\ln(x-1)+x-3=0\) equivale a risolvere l'equazione \(\ln(x-1)=-x+3\).
Ciò equivale a trovare l'ascissa dei punti di intersezione fra i grafici delle funzioni \(a(x)=\ln(x-1)\) e \(b(x)=-x+3\).
Osserviamo come si ottengono questi due grafici:
Osserviamo la figura in cui sono rappresentati i due grafici:
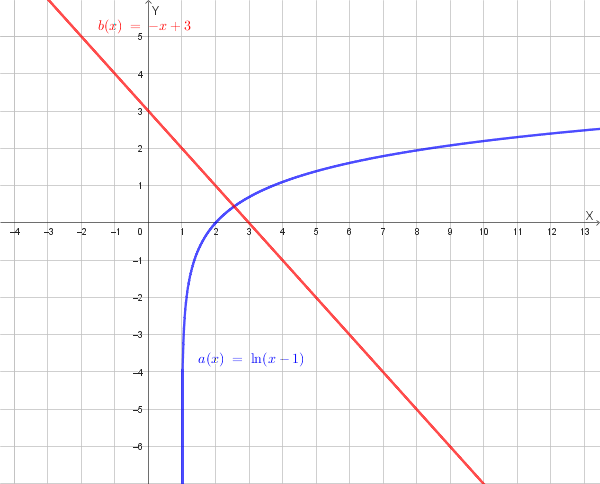
Dalla figura, e sapendo che una funzione è strettamente crescente e l'altra è strettamente decrescente, si deduce che i due grafici possono intersecarsi al massimo in un solo punto. Essendo stata dimostrata l'esistenza di una radice al punto a), ne consegue che tale radice è **unica** nell'intervallo \((2;3)\).
Per trovare un valore approssimato a meno di un decimo, tabuliamo i valori delle due funzioni \(a(x)\) e \(b(x)\) per valori compresi fra 2 e 3 con passo 0.1:
| \(x\) | \(a(x) = \ln(x - 1)\) | \(b(x) = -x + 3\) | \(a(x) > b(x)\) |
|---|---|---|---|
| 2.0 | 0.000 | 1.000 | Falso |
| 2.1 | 0.095 | 0.900 | Falso |
| 2.2 | 0.182 | 0.800 | Falso |
| 2.3 | 0.262 | 0.700 | Falso |
| 2.4 | 0.336 | 0.600 | Falso |
| 2.5 | 0.405 | 0.500 | Falso |
| 2.6 | 0.470 | 0.400 | Vero |
La soluzione si trova nel punto in cui \(a(x) = b(x)\). Dalla tabella, osserviamo che \(a(x)\) diventa maggiore di \(b(x)\) tra \(x=2.5\) e \(x=2.6\).
Questo significa che l'intersezione tra i due grafici, e quindi la radice dell'equazione, si trova nell'intervallo \((2.5; 2.6)\).
La radice approssimata a meno di 0.1 è **2.5 per difetto** e **2.6 per eccesso**.
Per tornare all'elenco completo dei compiti, clicca sul bottone in basso.