L'Integrale Definito - Matefilia.it

Definizione di Integrale di Riemann

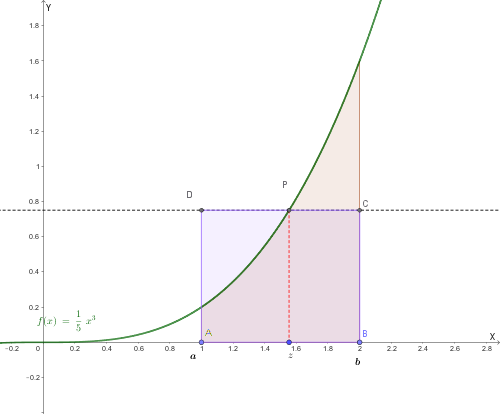
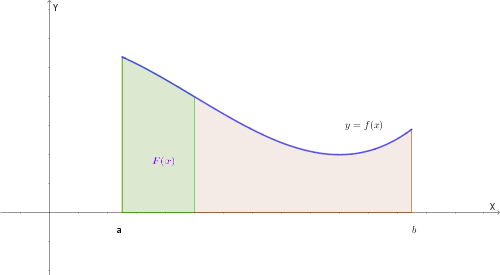
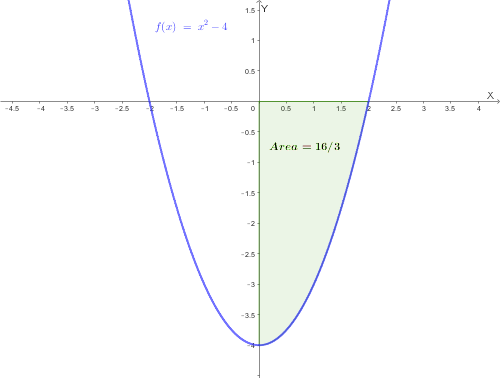
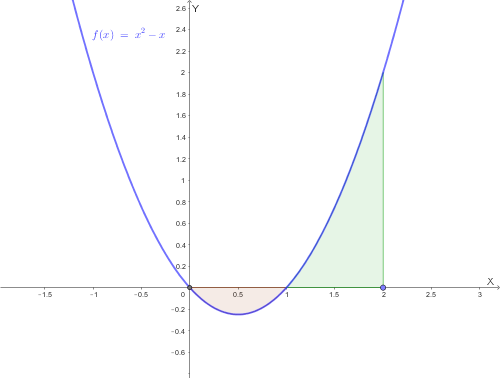
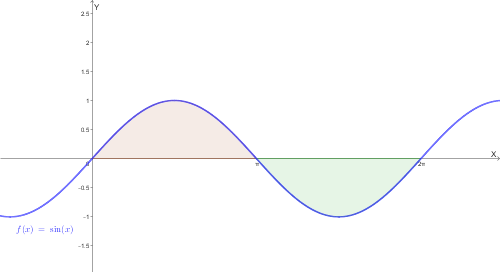
L'integrale definito nasce dall'esigenza geometrica di determinare l'area del trapezoide: la regione di piano delimitata dal grafico di una funzione \(f(x)\) (continua e non negativa), dall'asse \(x\) e dalle rette verticali \(x=a\) e \(x=b\).

1. Il calcolo per approssimazione (Plurirettangoli)

Dividiamo l'intervallo \([a, b]\) in \(n\) parti uguali, ciascuna di ampiezza:

\[ h = \frac{b-a}{n} \]

Sia \(m_i\) il valore minimo e \(M_i\) il valore massimo di \(f(x)\) in ogni intervallino. Definiamo:

Somma inferiore (Area plurirettangolo inscritto): \[ s_n = h \cdot m_1 + h \cdot m_2 + \dots + h \cdot m_n = h \sum_{i=1}^{n} m_i \]
Somma superiore (Area plurirettangolo circoscritto): \[ S_n = h \cdot M_1 + h \cdot M_2 + \dots + h \cdot M_n = h \sum_{i=1}^{n} M_i \]

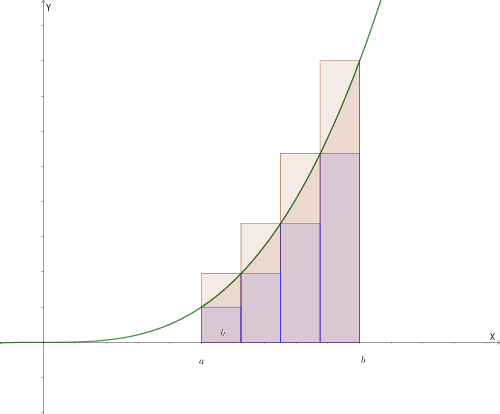
Esempio con 4 rettangoli

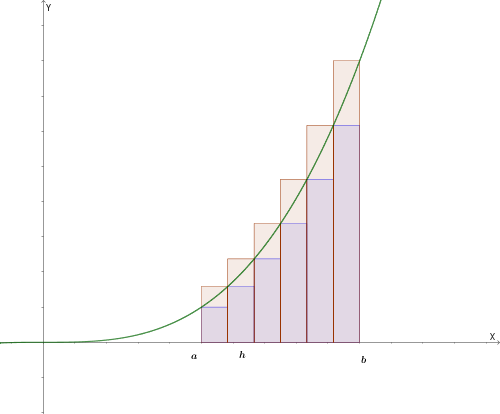
Esempio con 6 rettangoli

Per ogni \(n\), vale sempre la relazione: \[ s_n \le \text{Area del trapezoide} \le S_n \]

Osservazione: per \(n\) che tende all'infinito, \(s_n\) ed \(S_n\) tendono allo stesso valore, che rappresenta l'area del trapezoide.

2. Definizione formale di Integrale Definito

Prescindiamo ora dall'aspetto geometrico.

Consideriamo la funzione \(y=f(x)\) continua in un intervallo chiuso e limitato \([a,b]\). Suddividiamo l'intervallo in \(n\) intervalli di uguale ampiezza \(h=\frac{b-a}{n}\). Consideriamo i seguenti intervalli:

\(I_1=[a_0,a_1]\), dove \(a_0=a\) e \(a_1=a+h\)
\(I_2=[a_1,a_2]\), dove \(a_2=a+2h\)
...
\(I_n=[a_{n-1},a_n]\), dove \(a_n=b\)

Indichiamo con \(m_i\) ed \(M_i\) il minimo ed il massimo della funzione nell'intervallo \(i\)-esimo, osservando che tali minimi e massimi esistono per il Teorema di Weierstrass perché la funzione è continua in ognuno degli intervalli chiusi e limitati \(I_i\).

Definiamo le somme \(s_n\) ed \(S_n\) come sopra indicato. Poiché \(m_i \le M_i\) per ogni \(i\), si ha \(s_n \le S_n\) per ogni \(n\).

Se esistono finiti i limiti per \(n \to \infty\) di \(s_n\) e di \(S_n\), si può dimostrare che tali limiti sono uguali ad un unico valore finito \(L\). Si pone per definizione:

\[ \int_{a}^{b} f(x) \, dx = L = \lim_{n \to \infty} s_n = \lim_{n \to \infty} S_n \]

Elementi della notazione:

\(\int\): simbolo di integrale (una "S" stilizzata, che richiama il concetto di somma).
\(a, b\): estremi di integrazione (inferiore e superiore).
\(f(x)\): funzione integranda.
\(dx\): differenziale della variabile \(x\), che indica la variabile rispetto alla quale si integra.

Proprietà Fondamentali

Linearità: \(\int_{a}^{b} [kf(x) + hg(x)] dx = k \int_{a}^{b} f(x) dx + h \int_{a}^{b} g(x) dx\)
Additività rispetto all'intervallo: \(\int_{a}^{b} f(x) dx = \int_{a}^{c} f(x) dx + \int_{c}^{b} f(x) dx\) (valida per qualsiasi \(c\))
Inversione degli estremi: \(\int_{a}^{b} f(x) dx = -\int_{b}^{a} f(x) dx\)
Estremi coincidenti: \(\int_{a}^{a} f(x) dx = 0\)
Proprietà del confronto (Monotonia):
Se \(f(x)\) e \(g(x)\) sono due funzioni continue e tali che \(f(x) \le g(x)\) in ogni punto dell'intervallo \([a, b]\), allora:
\[ \int_{a}^{b} f(x) \, dx \le \int_{a}^{b} g(x) \, dx \]

Conseguenza importante (Positività):

Se \(f(x) \ge 0\) in \([a, b]\), allora l'integrale \(\int_{a}^{b} f(x) \, dx \ge 0\).

Se \(f(x)\) è continua in \([a, b]\), esiste almeno un punto \(z \in [a, b]\) tale che:

\[ f(z) = \frac{1}{b-a} \int_{a}^{b} f(x) \, dx \]

Geometricamente, esiste un rettangolo di base \((b-a)\) e altezza \(f(z)\) che ha la stessa area della regione sottesa dalla curva.

Esempio di applicazione:

Data la funzione \(f(x) = \frac{1}{5}x^3\) nell'intervallo \([1, 2]\), determiniamo il valore di \(z\).

1. Calcolo dell'integrale:

Per il Teorema fondamentale del calcolo integrale (che vedremo successivamente), detta \((F(x)\) una primitiva di \(f(x)\), risulta:

\[ \int_{a}^{b} f(x) \, dx = [F(x)]_a^b = F(b) - F(a) \]

Nel nostro caso:

\[ \int_{1}^{2} \frac{1}{5}x^3 \, dx = \left[ \frac{x^4}{20} \right]_1^2 = \frac{2^4}{20} - \frac{1^4}{20} = \frac{16}{20} - \frac{1}{20} = \frac{15}{20} = \frac{3}{4} \]

2. Applicazione della formula della media:

Poiché \(b-a = 2-1 = 1\), si ha:

\[ f(z) = \frac{1}{1} \cdot \frac{3}{4} = 0,75 \]

3. Ricerca di \(z\):

\[ \frac{1}{5}z^3 = 0,75 \implies z^3 = 3,75 \implies z = \sqrt[3]{3,75} \approx 1,55 \]

Il valore \(z \approx 1,55\) appartiene all'intervallo \([1, 2]\), come previsto dal teorema.

Rappresentazione geometrica del teorema della media

Rappresentazione geometrica dell'esempio

Esempio 2: Calcolo del Valor Medio

Determiniamo il valor medio della funzione \(f(x) = \sin(x)\) nell'intervallo \([0, \pi]\).

1. Calcolo dell'integrale (Area sottesa):

Utilizziamo la primitiva \(F(x) = -\cos(x)\):

\[ \int_{0}^{\pi} \sin(x) \, dx = [-\cos(x)]_0^{\pi} = -\cos(\pi) - (-\cos(0)) = -(-1) - (-1) = 1 + 1 = 2 \]

2. Calcolo del valor medio (\(y_m\)):

L'ampiezza dell'intervallo è \(b - a = \pi - 0 = \pi\). Applicando la formula del valore medio:

\[ y_m = \frac{1}{\pi} \int_{0}^{\pi} \sin(x) \, dx = \frac{2}{\pi} \approx 0,637 \]

Interpretazione: Il valore medio rappresenta l'altezza di un rettangolo che ha la stessa base dell'intervallo (\(\pi\)) e la stessa area della regione sottesa dalla sinusoide (Area = 2).

Il valor medio della funzione seno in [0, π]

1. La Funzione Integrale

Sia \(f(t)\) una funzione continua in \([a, b]\). Definiamo funzione integrale di \(f\) in \([a, b]\) la funzione \(F(x)\) che associa ad ogni \(x \in [a, b]\) il valore dell'integrale definito nell'intervallo \([a, x]\):

\[ F(x) = \int_{a}^{x} f(t) \, dt \]

Significato geometrico: \(F(x)\) rappresenta l'area (con segno) della regione di piano compresa tra il grafico di \(f\), l'asse delle ascisse e le rette verticali di equazione \(t=a\) e \(t=x\). Al variare di \(x\), tale area "si accumula" o "diminuisce" a seconda del segno della funzione.

Significato geometrico della funzione integrale

\(F(x) = \int_{a}^{x} f(t) \, dt\)

2. Il Teorema Fondamentale del Calcolo

Questo teorema stabilisce un legame profondo tra calcolo integrale e calcolo differenziale. Se \(f(x)\) è continua in \([a, b]\), allora la funzione integrale \(F(x)\) è derivabile in tutto l'intervallo e la sua derivata coincide con la funzione integranda:

\[ F'(x) = f(x) \quad \text{ovvero} \quad \frac{d}{dx} \left[ \int_{a}^{x} f(t) \, dt \right] = f(x) \]

In sintesi: la funzione integrale è una primitiva di \(f(x)\). Questo implica che l'integrazione è l'operazione inversa della derivazione.

3. La Formula di Leibniz-Newton

Dal teorema precedente discende la regola pratica per il calcolo degli integrali definiti. Se \(G(x)\) è una qualunque primitiva di \(f(x)\), allora:

\[ \int_{a}^{b} f(x) \, dx = [G(x)]_a^b = G(b) - G(a) \]

Cenni sulla dimostrazione: Poiché \(F(x)\) (funzione integrale) e \(G(x)\) sono entrambe primitive di \(f(x)\), esse differiscono per una costante \(c\): \(G(x) = F(x) + c\).
Calcolando la differenza negli estremi: \(G(b) - G(a) = [F(b) + c] - [F(a) + c] = F(b) - F(a)\).
Sapendo che \(F(a) = \int_{a}^{a} f(t)dt = 0\), si ottiene: \(G(b) - G(a) = F(b) = \int_{a}^{b} f(x)dx\).

Esempio di calcolo:

Calcoliamo \(\int_{1}^{2} 3x^2 \, dx\):

Una primitiva di \(f(x) = 3x^2\) è \(G(x) = x^3\). Applichiamo la formula:

\[ \int_{1}^{2} 3x^2 \, dx = [x^3]_1^2 = G(2) - G(1) = 2^3 - 1^3 = 7 \]

L'area \(A\) della regione di piano compresa tra il grafico di \(f(x)\), l'asse \(x\) e le rette \(x=a\) e \(x=b\) è data dall'integrale del valore assoluto della funzione:

\[ A = \int_{a}^{b} |f(x)| \, dx \]

1. Funzione positiva o nulla (\(f(x) \ge 0\))

Esempio: Area sottesa da \(f(x) = x^2\) in \([0, 2]\).

Siccome \(x^2 \ge 0\):
\[ A = \int_{0}^{2} x^2 dx = \left[ \frac{x^3}{3} \right]_0^2 = \frac{8}{3} \]

2. Funzione negativa o nulla (\(f(x) \le 0\))

Esempio: Area tra \(f(x) = x^2 - 4\) e l'asse \(x\) in \([0, 2]\).

In questo intervallo la parabola è negativa, quindi cambiamo segno all'integrale:
\[ A = - \int_{0}^{2} (x^2 - 4) dx = \frac{16}{3} \]

3. Funzione con segno variabile

Bisogna spezzare l'integrale nei punti di zero e sommare i valori assoluti dei singoli contributi.

Esempio: Differenza tra Integrale e Area

Per \(f(x) = x^2 - x\) in \([0, 2]\), l'integrale definito è \(2/3\), ma l'area reale è:

\[ A = \left| \int_{0}^{1} (x^2 - x) dx \right| + \int_{1}^{2} (x^2 - x) dx = \frac{1}{6} + \frac{5}{6} = 1 \]

Il caso limite: Se le aree sono uguali e opposte, l'integrale è nullo ma l'area no.

Esempio: Area di \(f(x) = \sin(x)\) in \([0, 2\pi]\).

L'integrale è \(0\), ma l'area geometrica è:
\[ A = \int_{0}^{\pi} \sin(x) dx + \left| \int_{\pi}^{2\pi} \sin(x) dx \right| = 2 + 2 = 4 \]