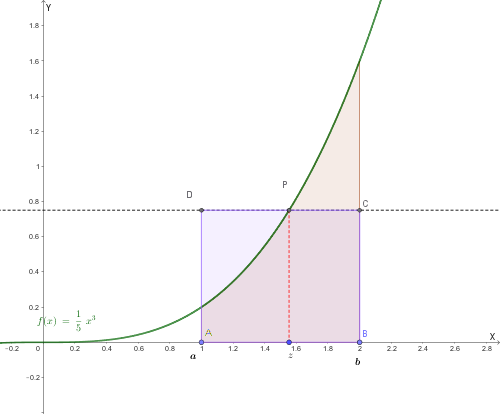
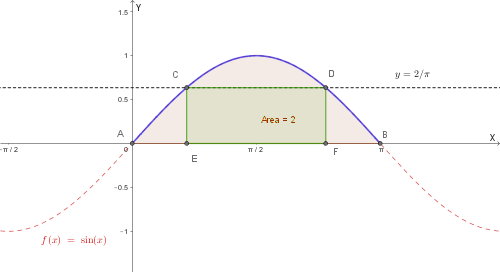
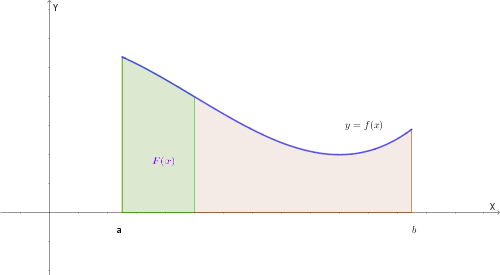
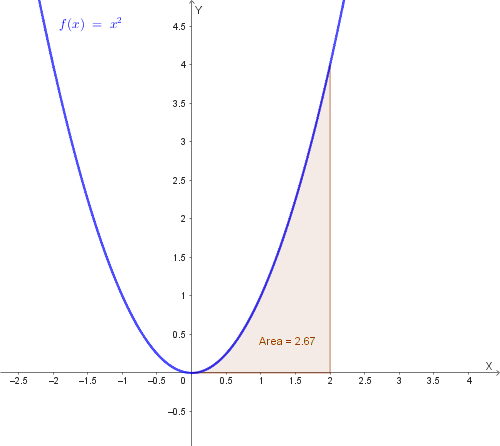
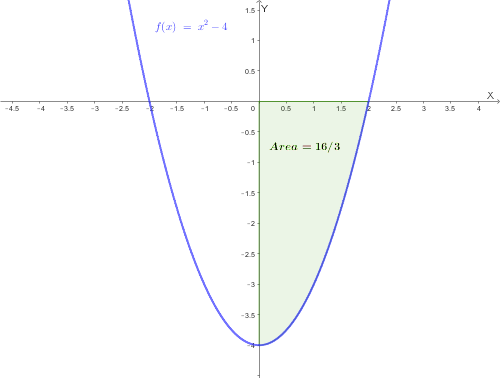
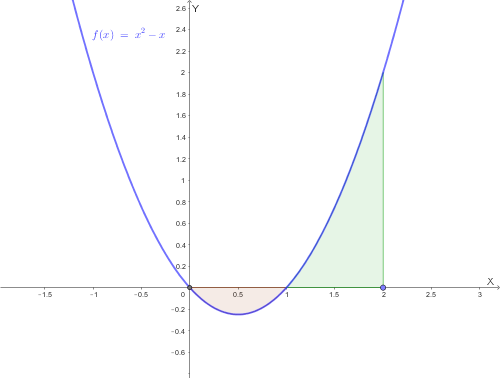
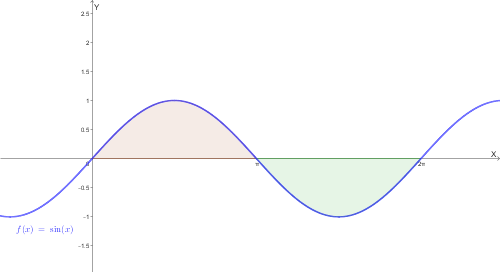
L'Integrale Definito

L'integrale definito serve per calcolare l'area del trapezoide (la figura sotto il grafico della funzione).

1. Approssimazione con i Plurirettangoli

Per calcolare l'area, dividiamo la base in tanti rettangoli.

Osserva come cambia l'approssimazione:

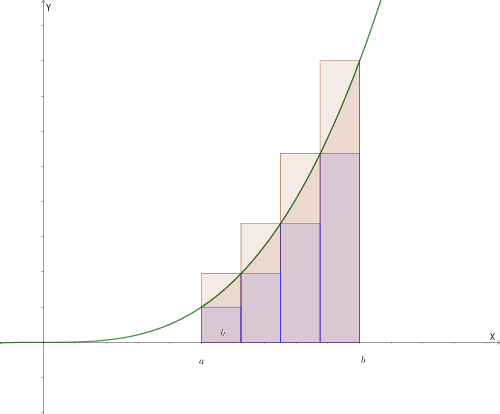
Figura A: Approssimazione con 4 rettangoli (molto spazio vuoto).

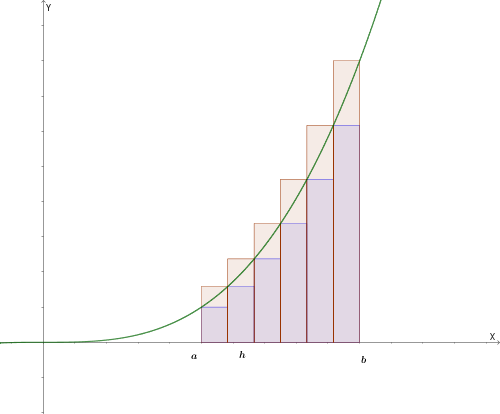
Figura B: Approssimazione con 6 rettangoli (l'errore diminuisce).

Conclusione visiva: Più rettangoli usiamo, più la somma delle loro aree si avvicina all'area reale.

2. Definizione e Simboli

Quando il numero dei rettangoli diventa infinito, otteniamo l'integrale definito.

\int_{a}^{b} f(x) \, dx

Elementi della notazione:

🟢 $\int$ : simbolo di integrale (una "S" stilizzata per indicare la Somma).
🟢 $a, b$ : estremi di integrazione (punto di inizio e punto di fine).
🟢 $f(x)$ : funzione integranda (la curva di cui vogliamo l'area).
🟢 $dx$ : indica la variabile rispetto alla quale stiamo calcolando (la variabile $x$).

La Proprietà di Linearità

La linearità ci permette di "spezzare" gli integrali complicati in parti più semplici. Si divide in due regole:

1. Somma di funzioni: l'integrale di una somma è uguale alla somma degli integrali. $\int (f+g) = \int f + \int g$
2. Prodotto per una costante: i numeri moltiplicati (le costanti) possono essere "portati fuori" dal simbolo di integrale. $\int k \cdot f = k \cdot \int f$

Formula completa di Linearità:

\int_{a}^{b} [k \cdot f(x) + h \cdot g(x)] \, dx = k \int_{a}^{b} f(x) \, dx + h \int_{a}^{b} g(x) \, dx

Altre proprietà importanti

Additività: se prendiamo un punto $c$ tra $a$ e $b$, possiamo spezzare l'area in due parti: $\int_{a}^{b} = \int_{a}^{c} + \int_{c}^{b}$
Inversione degli estremi: se scambiamo l'ordine di $a$ e $b$, il risultato cambia segno: $\int_{a}^{b} f(x) \, dx = - \int_{b}^{a} f(x) \, dx$
Confronto (Monotonia): se una funzione è sempre più alta di un'altra ($f \ge g$), anche la sua area sarà maggiore.

Il teorema ci dice che esiste un valore medio della funzione in un intervallo.

Le condizioni (Ipotesi):

La funzione $f(x)$ deve essere continua.
L'intervallo $[a, b]$ deve essere chiuso e limitato.

Enunciato del Teorema

Esiste almeno un punto $z$ nell'intervallo tale che l'area del trapezoide è uguale a quella di un rettangolo avente per base la stessa base e per altezza il valore della funzione in $z$:

\int_{a}^{b} f(x) \, dx = (b - a) \cdot f(z)

Il valore $f(z)$ è il Valore Medio della funzione.

L'area della regione colorata è uguale a quella del rettangolo tratteggiato.

Esempio 1: Ricerca del punto $z$

Data la funzione $f(x) = \frac{1}{5}x^3$ nell'intervallo $[1, 2]$, determiniamo il valore di $z$.

1. Calcolo dell'integrale:

\int_{1}^{2} \frac{1}{5}x^3 \, dx = \left[ \frac{x^4}{20} \right]_1^2 = \frac{16}{20} - \frac{1}{20} = \mathbf{\frac{15}{20} = \frac{3}{4}}

2. Applicazione della formula della media:

Poiché la base è $b-a = 2-1 = 1$, si ha:

f(z) = \frac{1}{1} \cdot \frac{3}{4} = \mathbf{0,75}

3. Ricerca di $z$:

\frac{1}{5}z^3 = 0,75 \implies z^3 = 3,75 \implies z = \sqrt[3]{3,75} \approx \mathbf{1,55}

Il valore $z \approx 1,55$ appartiene all'intervallo $[1, 2]$.

Esempio 2: Calcolo del Valor Medio

Determiniamo il valor medio della funzione $f(x) = \sin(x)$ nell'intervallo $[0, \pi]$.

1. Calcolo dell'area sottesa:

\int_{0}^{\pi} \sin(x) \, dx = [-\cos(x)]_0^{\pi} = -(-1) - (-1) = \mathbf{2}

2. Calcolo del valor medio ($y_m$):

L'ampiezza dell'intervallo è $\pi$. Applichiamo la formula:

y_m = \frac{1}{\pi} \int_{0}^{\pi} \sin(x) \, dx = \mathbf{\frac{2}{\pi} \approx 0,637}

Interpretazione: Il valore medio rappresenta l'altezza del rettangolo equivalente.

Questo teorema è il "ponte" che collega il calcolo delle aree (integrali) con il calcolo delle derivate.

1. La Funzione Integrale

Immaginiamo che l'estremo superiore dell'integrale non sia un numero fisso, ma una variabile $x$. Definiamo la funzione integrale $F(x)$:

F(x) = \int_{a}^{x} f(t) \, dt

Significato geometrico:

$F(x)$ rappresenta l'area che si "accumula" partendo dal punto $a$ fino al punto variabile $x$.

L'area colorata varia al variare di $x$.

2. Il Teorema Fondamentale del Calcolo

Il teorema stabilisce che la funzione integrale $F(x)$ è una primitiva della funzione $f(x)$. In formule:

\[ F'(x) = f(x) \]

In sintesi: l'integrazione è l'operazione inversa della derivazione.

3. La Formula di Leibniz-Newton

Questa è la regola pratica per calcolare gli integrali. Se $G(x)$ è una primitiva di $f(x)$, allora:

\int_{a}^{b} f(x) \, dx = [G(x)]_a^b = G(b) - G(a)

Cenni sulla dimostrazione:

🔹 $F(x)$ e $G(x)$ sono entrambe primitive, quindi differiscono per una costante: $G(x) = F(x) + c$.
🔹 Facciamo la differenza: $G(b) - G(a) = [F(b) + c] - [F(a) + c] = F(b) - F(a)$.
🔹 Poiché $F(a) = 0$ (l'area in un punto è nulla), resta: $G(b) - G(a) = F(b)$.
🔹 Ma $F(b)$ è proprio l'integrale tra $a$ e $b$. Fine!

Esempio di calcolo:

Calcoliamo $\int_{1}^{2} 3x^2 \, dx$:

Trovo la primitiva: La primitiva di $3x^2$ è $G(x) = x^3$.
Applico la formula: $\[ [x^3]_1^2 = G(2) - G(1) \]$
Sostituisco i valori: $2^3 - 1^3 = 8 - 1 = \mathbf{7}$

Per calcolare l'Area geometrica ($A$) bisogna fare attenzione al segno della funzione. La formula generale usa il valore assoluto:

A = \int_{a}^{b} |f(x)| \, dx

1. Funzione positiva o nulla ($f(x) \ge 0$)

Se la funzione è tutta sopra l'asse $x$, l'area coincide con l'integrale.

Esempio: Area di $f(x) = x^2$ in $[0, 2]$.

Siccome $x^2$ è sempre positiva:

A = \int_{0}^{2} x^2 \, dx = \left[ \frac{x^3}{3} \right]_0^2 = \mathbf{\frac{8}{3}}

2. Funzione negativa o nulla ($f(x) \le 0$)

Se la funzione è sotto l'asse $x$, l'integrale viene negativo. Per avere l'area (che è sempre positiva) dobbiamo cambiare segno.

Esempio: Area tra $f(x) = x^2 - 4$ e l'asse $x$ in $[0, 2]$.

In questo intervallo la curva è negativa, quindi:

A = - \int_{0}^{2} (x^2 - 4) \, dx = - \left[ \frac{x^3}{3} - 4x \right]_0^2 = \mathbf{\frac{16}{3}}

3. Funzione con segno variabile

Dobbiamo spezzare l'integrale nei punti in cui la funzione taglia l'asse $x$ (gli zeri).

Esempio: Differenza tra Integrale e Area

Per $f(x) = x^2 - x$ in $[0, 2]$:

Tra 0 e 1 la funzione è negativa.
Tra 1 e 2 la funzione è positiva.

A = \left| \int_{0}^{1} (x^2 - x) \, dx \right| + \int_{1}^{2} (x^2 - x) \, dx = \frac{1}{6} + \frac{5}{6} = \mathbf{1}

⚠️ Il caso limite: Se le aree sopra e sotto sono uguali, l'integrale totale è zero, ma l'area geometrica no!

Esempio: Area di $f(x) = \sin(x)$ in $[0, 2\pi]$.

L'integrale è 0, ma l'area reale è:

A = \int_{0}^{\pi} \sin(x) \, dx + \left| \int_{\pi}^{2\pi} \sin(x) \, dx \right| = 2 + 2 = \mathbf{4}