SOLUZIONI SOLUZIONI

2001

1) Rompicapo probabilistico.

Si hanno due urne così composte:
  
      U1 contiene  10 palline nere e   5 palline bianche
      U2 contiene    8  palline nere e   10 palline bianche.

Si lancia un dado e se escono i numeri 1 o 2 si estrae una pallina dalla prima urna, altrimenti se ne estrae una dalla seconda. Se questa prima pallina estratta è nera, allora la si rimette nell'urna e si estrae un'altra pallina dall'urna che non conteneva la prima.
Rappresenta la situazione con un grafo ad albero.
Nell'ipotesi che l'ultima pallina estratta, cioè la pallina visibile fuori dall'urna, sia bianca, calcola la probabilità che essa provenga dalla prima urna.

Adobe® Acrobat® Reader è il software che vi permette di visualizzare e stampare i file in formato Adobe Portable Document Format (PDF) sulle principali piattaforme di computer.

La soluzione di Luigi Bernardini

La soluzione di Rocco Lupoi (esteticamente non eccezionale ma, al solito, efficace)

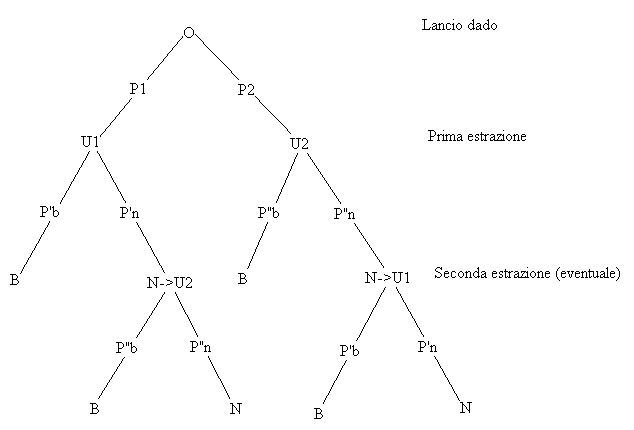
Indicando con ' le situazioni della prima scelta e con " quelle della
seconda scelta, con ovvio significato dei simboli, si ha che:

P(B')=P(B'/U'1)P(U'1)+P(B'/U'2)P(U'2); P(B")=P(B"/U"2)P(U"2)+P(B"/U"1)P(U"1)
P(U"2)=P(N'/U'1)P(U'1);P(U"1)=P(N'/U'2)P(U'2);
P(B) = P(B')+P(B").

Posto U1= U'1 U U"1, il problema chiede di trovare P(U1/B).

Per il teorema di Bayes, si ha che P(U1/B)=P(B/U1)P(U1)/P(B).

Indico con P1 e P2 le probabilita' di scelta dell'urna U1 e U2
rispettivamente con il lancio del dado, con P'b e P'n le probabilita' di
scelta di una pallina bianca e nera rispettivamente dall'urna U1 e con P"b e
P"n le probabilita' di scelta di una pallina bianca e nera rispettivamente
dall'urna U2.

Quindi P(B)=P'b*P1+P"b*P2+P"b*P'n*P1+P'b*P"n*P2, P(B/U1)=P'b e
P(U1)=P1+P2*P"n.

Nel nostro caso P1=1/3,P2=2/3,P'b=1/3,P'n=2/3,P"b=5/9 e P"n=4/9.

Percio' P(B)=19/27, P(B/U1)=1/3 e P(U1)=17/27 quindi
P(U1/B)=1/3*17/27*27/19=17/57.

##########

Un modo equivalente per giungere allo stesso risultato e' questo:

P(B)=P(B/U1)P(U1)+P(B/U2)P(U2) con P(U1)=P1+P2*P"n e P(U2)=P2+P1*P'n

a questo punto si prosegue come prima:

dato che P(B)P(B/U1)=P(U1)P(U1/B) si ha P(U1/B)=P(B/U1)P(U1)/P(B).

La soluzione di Sergio Natale

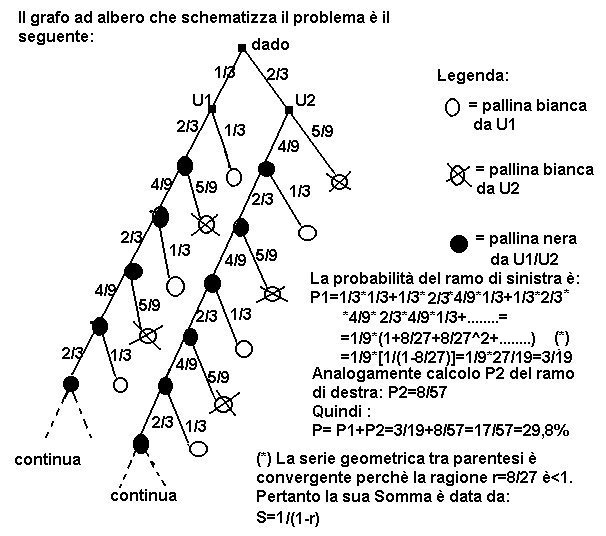
La soluzione di Maurizio Castellan