A. S. 1998/99
M557 – ESAME DI
STATO LICEO SCIENTIFICO
CORSO DI ORDINAMENTO
Tema di: MATEMATICA
Il candidato scelga a suo piacimento due dei seguenti problemi e li
risolva:
- Sia f(x) una funzione reale di variabile reale derivabile in un punto x0.
- Dire se la condizione f ’(x0) = 0 è:
- necessaria ma non sufficiente,
- sufficiente ma non necessaria,
- necessaria e sufficiente
per concludere che la funzione ha un estremo relativo nel punto x0.
Fornire una esauriente dimostrazione della risposta.
- Posto
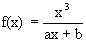 , dove a, b sono
parametri reali, determinare tali parametri in modo che la curva g
di equazione cartesiana y = f(x) abbia un estremo relativo nel punto di coordinate
, dove a, b sono
parametri reali, determinare tali parametri in modo che la curva g
di equazione cartesiana y = f(x) abbia un estremo relativo nel punto di coordinate 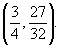
- Controllato che la curva g cercata si ottiene per a = 2,
studiare tale curva e disegnarne l’andamento in un piano riferito ad un sistema di
assi cartesiani ortogonali (Oxy).
- Nello stesso piano (Oxy) disegnare l’andamento della curva g
’ di equazione y = f ’(x), dopo aver determinato, in particolare, le coordinate
dei punti comuni a g e g ’.
- Sussiste un’evidente relazione fra l’andamento di g
e quello di g ’. Quale?
- In un piano a sono assegnate una circonferenza k di raggio di
lunghezza data r ed una parabola p passante per gli estremi A, B di un diametro di k e
avente come asse di simmetria l’asse del segmento AB. L’area del segmento
parabolico delimitato dalla parabola p e dal segmento AB è
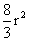
.
Dopo aver riferito il piano a ad un
conveniente sistema di assi cartesiani (Oxy):
- determinare l’equazione della circonferenza k;
- determinare l’equazione della parabola p;
- trovare le coordinate dei punti comuni a k e p;
- calcolare le aree delle regioni piane in cui la parabola p divide il cerchio delimitato
da k;
- stabilire per quale valore di r la maggiore di tali aree è uguale a
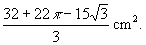
- Considerato il quadrato ABCD, sull’arco di circonferenza di centro A e raggio AB,
contenuto nel quadrato, si prenda un punto T in modo che l’angolo
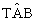
misuri 2x radianti. Si conduca quindi per T la retta tangente alla circonferenza e si
chiamino P e Q i punti in cui essa seca le rette BC e CD rispettivamente.
- Esprimere in funzione di x il rapporto:
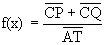
- Studiare la funzione f(x) ottenuta, tenendo conto dei limiti imposti alla variabile x
dalla questione geometrica, e disegnarne il grafico in un piano cartesiano ai fini della
risoluzione del punto c).
- Utilizzare il grafico disegnato per determinare x in modo che il rapporto considerato
sia uguale ad un numero reale k assegnato.
- Verificare che il rapporto f(x) può essere scritto nella seguente forma:
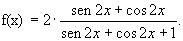
- Stabilire che risulta:
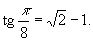
________________________________________
Durata massima della prova: 5 ore.
E’ consentito l’uso della calcolatrice tascabile non
programmabile.
Non è consentito lasciare l'Istituto prima che siano trascorse 3 ore
dalla dettatura del tema.
LE SOLUZIONI

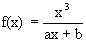 , dove a, b sono
parametri reali, determinare tali parametri in modo che la curva g
di equazione cartesiana y = f(x) abbia un estremo relativo nel punto di coordinate
, dove a, b sono
parametri reali, determinare tali parametri in modo che la curva g
di equazione cartesiana y = f(x) abbia un estremo relativo nel punto di coordinate